位标器陀螺转轴静平衡测试系统设计
杨 辉 赵 剡 李 敏
(北京航空航天大学 仪器科学与光电工程学院,北京100191)
位标器是利用陀螺的进动性和定轴性来调整和稳定导弹导引头光学系统的装置.通常由于设计误差、材料缺陷、加工与装配误差等原因会造成位标器陀螺转轴产生质量偏心,从而引起位标器静不平衡,不平衡量如果太大,就会引起光轴的绕动,使输出目标信号不稳定而影响导弹的命中精度和飞行平稳度,因此,为提高导弹的制导精度和可靠性,对位标器的静不平衡特性进行研究和测试很有必要[1-3].
传统的位标器静平衡测试方法有菱形导轨平衡法、辊轴平衡法、静压支撑法及天平平衡法等,与这些方法相对应的则是一些普遍存在着较大摩擦力,装拆比较困难的纯机械物理系统,难以达到很高的测试精度.文献[4]提到将被测转子放置在水平面间隔120°的3个压力传感器上来测其不平衡量的大小和相位,该方法虽然操作简单,但是仅适用于二维空间的静不平衡特性测试,并且鉴于单纯的裸露传感器,其精度相对较低.文献[5]提到将陀螺转子放在一个高精度电子天平上,通过不断调整来测定其静不平衡量的大小和方位,该方法虽然理论依据简单,对测试系统的硬件要求不高,但却只能测试特殊结构的陀螺转子,而且不能进行高精度转子的静平衡测量[6-7].光学调整法虽在很大程度上克服了纯机械物理系统测试方法的不足,但它对测试环境要求较高,适应性较差,测试效率难以提高[8].
针对上述各种测试系统的不足,研制了一种新型静平衡测试系统用于对位标器陀螺转轴的静不平衡量及其位置进行测试并配重,该测试系统使用多功能、高精度的数据采集卡记录陀螺位标器各个轴运动的角度、角速度、驱动电压和电流,并采用图形化编程软件Lab VIEW语言作为开发工具进行系统监控与数据处理,具有较高的可靠性、运行效率和较直观的软件操作界面.
1 系统的组成及其功能
位标器转轴静平衡测试系统的构成如图1所示,包括水平轴角位置转台及其驱动器、工装夹具、电源模块、模拟件、控制器、多功能数据采集卡、适配器等.
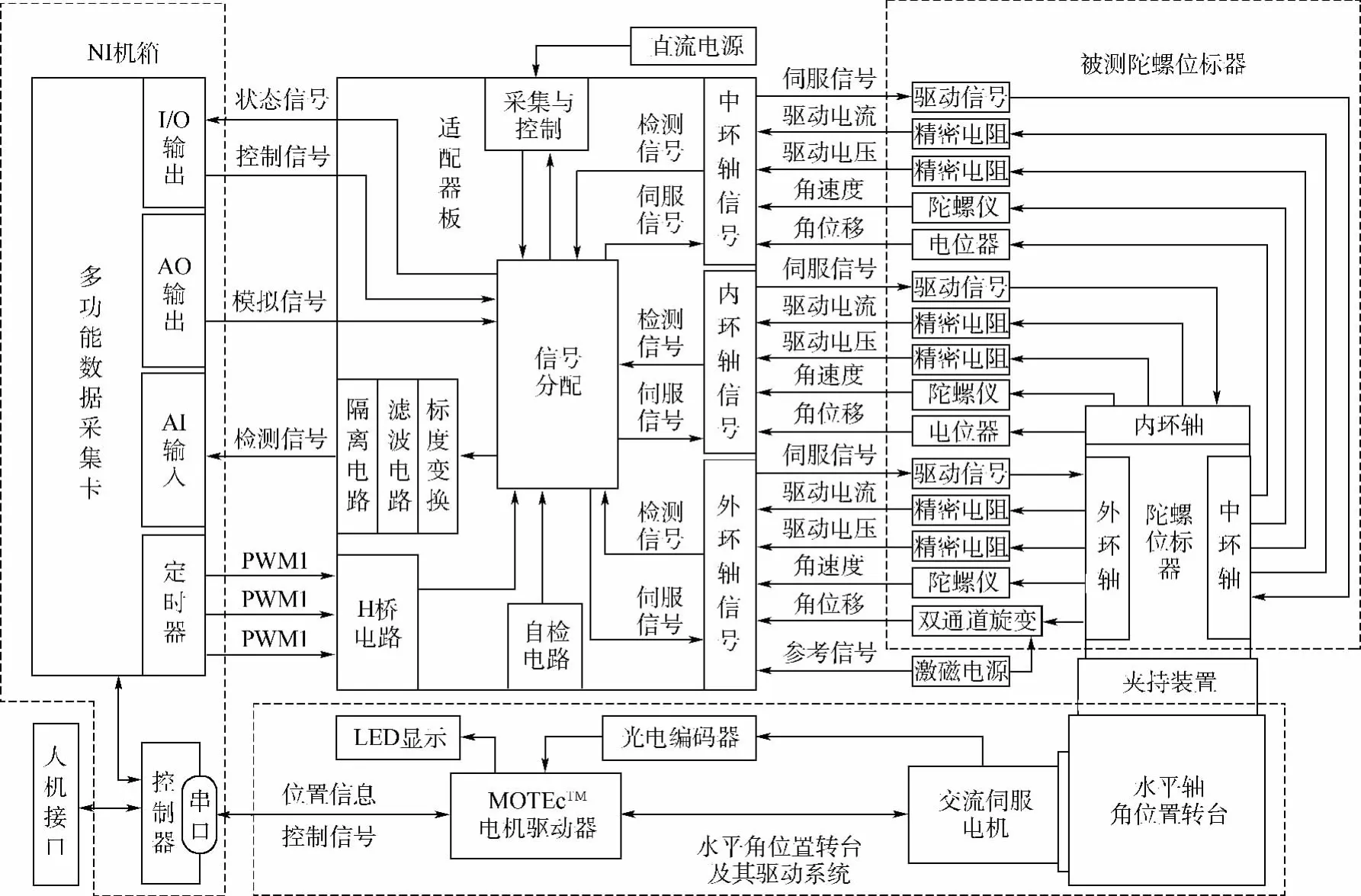
图1 3陀螺位标器转轴静平衡测试系统的构成
该系统的各个组成部分的功能如下:
1)水平轴角位置转台及其驱动器:水平轴角位置转台用来装卡被测位标器,MOTEcTMα型的交流伺服电机驱动器通过RS232方式接收测控系统(上位机)发出的角位置控制信号驱动转台到达不同的角位置锁定,同时将转台的实时位置以光电编码器反馈至驱动器.水平轴角位置转台的定位精度不低于0.2',转角范围不小于360°.
2)电源模块:+27 V/6 A和+6 V/3 A依次用来给位标器3个转轴电机和陀螺供电;±15 V/2 A用于适配器供电;±12 V/2 A用来给中环及内环转轴的角位移检测元件电位器供电;20 V/1 A,800 Hz的交流电源用来给外环转轴的角位移检测元件旋变供电,并作为角位移解算时的参考信号使用.
3)模拟件:模拟件是一个已经人为校准过的配平件,用来校验对外环静不平衡测试的精度.
4)控制器PXI-8102:它是静平衡测试系统的核心,在其上采用Lab VIEW语言作为开发工具,以动画、图表和虚拟面板的形式实现对所有设备、模块的监控,并完成对测试数据的处理.
5)多功能数据采集卡PXIe-6363:数据采集卡和控制器PXI-8102都插在PXI机箱的插槽上,PXIe-6363接受PXI-8102的指令进行工作,一方面通过它的3个定时器输出口输出不同的3列PWM(Pulse Width Modulation)波,这3列不同的PWM波配合6路数字I/O口输出的3路不同的电机起/停信号和3路不同的方向控制信号来合成3路不同的伺服驱动信号去驱动适配器上3个不同的H桥电路,从而驱动陀螺位标器3个转轴进行动作,另一方面还要通过其上的3个数字I/O口完成对直流电源的采集与比较;PXIe-6363模拟输入口的功能则是实时地对位标器陀螺转轴的转动角度、角速度、驱动电流、电压进行采集.
6)适配器:适配器上除有和多功能数据采集卡相连的两个接口外,还有电源供电输入接口、位标器的测试接口、自检电路.适配器除用来完成对各种采集信号的标度变换、滤波等作用外,还用来完成对设备的自检,对来自数据采集卡的数字控制信号的放大和分配.
2 系统的测试原理
2.1 静不平衡量测试的原理
假设当前时刻,测控系统驱动水平轴角位置转台锁定在预先设定的第i个角位置θi处,此时,位标器没有被选作被测轴的另外两个轴处于锁定状态,用图2所示的圆面表示被测轴正在绕其轴线进行往复正弦小角度运动,被测轴运动的结果使得其端面圆周上,偏心质量为m的点也沿弧段AB,以C为中心进行往复正弦小角度运动.
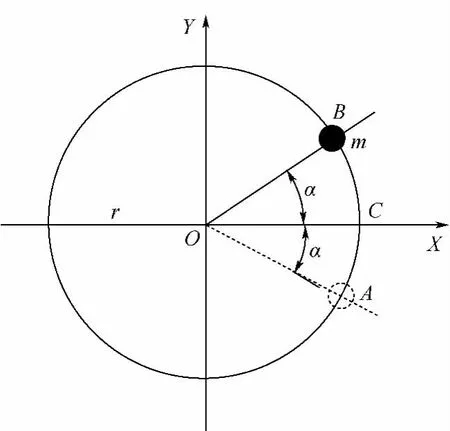
图2 被测轴转矩特性分析
在水平轴角位置转台锁定的第i个角位置θi处,假设偏心质量m所在的半径r与X轴正向的夹角为α,被测轴的转动惯量为J,转矩常数为KT,阻尼系数为C,弹性系数为F,被测轴电机输出的力矩为M',驱动电流为ii,此时所受的总力矩为M,静不平衡力矩为Mθi,则被测轴的惯性力矩为J,所受的阻力矩为Cα˙,所受的恢复力矩为Fα,根据刚体力学的知识可得[9-10]

由力矩平衡关系可知:

假设用t2i与t1i分别表示被测轴在第i次测试中,电流测量量多周期积分的上下限时刻,把式(1)代入式(2),并进行积分运算得


由式(4)可知,通过对被测轴驱动电流测量量的多个整周期积分就可以估计出θi角位置处,偏心质量m所受的静不平衡力矩量Mθi.
2.2 静不平衡量所处位置测试的原理
将位标器装卡到水平轴角位置转台上,通过调整安装夹具的方向使位标器的任意一个被测轴与转台水平轴平行,如图3所示,记录完它们各自的零位后,由测控系统驱动转台依次锁定在每一个预先设定的角位置θi处(本文取i=36),在每个θi处,再由测控系统驱动位标器的被测轴以α正弦小角度振动,匀速情况下排除加速力矩影响,小角度范围内(如-2°~+2°),偏心质量m所受的静不平衡力矩量Mθi可以认为是常值,而在转台不同角位置时,因为同一小角度区间内静不平衡力矩正弦变化,摩擦力矩与阻力矩等近似不变,所以,据此可在二维坐标平面内绘出理想情况下,Mθi-θi的关系曲线(至少绘够θi的一个周期)如图4所示.

图3 角位置转台及被测轴转动示意图

图4 被测轴的Mθi-θi曲线
从图4观察出最大静不平衡量所对应的转台角位置θ0后,再将归零位之后的转台按之前测试时的运转方向,使其转动θ0,如果转台之前测试时的运转方向和图3相同,那么此时静不平衡量的位置应处在图3中陀螺位标器被测轴的P1(P'1)处,配重位应在P2(P'2)处[11-13].图4 绘出的是理想情况下的关系曲线.
由于各种干扰的存在,根据实际测试数据描出的Mθi-θi的关系曲线变形比较严重,要从其测试数据或者从图4中得出被测轴的静不平衡量及静不平衡位置非常困难,此时,可以借助最小二乘法,通过对Mθi-θi进行拟合来求出静不平衡量及静不平衡位置,具体算法在后面介绍.
2.3 被测轴正弦小角度运动的控制
位标器被测轴进行正弦小角度运动时的控制性能对其转轴静平衡测试的精度具有决定意义,根据测试系统的原理及方案要求,外环直流力矩电机采用J94XFS001型双通道旋转变压器(中环与内环轴采用电位器,控制方法与外环类似)与XK109B型陀螺仪分别进行角位置与角速度的反馈,构成的直流力矩电机双闭环变速PID(Proportion Integration Differentiation)控制系统如图5所示.

图5 外环力矩电机PID双闭环控制系统框图
因为普通PID控制,积分系数取大了会产生超调,甚至是积分饱和,取小了又迟迟不能消除静差,所以就要设法改变积分项的累加速度,使其与偏差大小相对应,偏差越大,积分越慢,反之则越快.为此,设置系数f(e(i)),它不仅是误差e(i)的函数,而且与e(i)设定值的范围大小S也有一定的关系.为防止微分信号引入高频干扰,在微分环节中,还引入了不完全微分.综上所述,本文设计的变速PID如下:
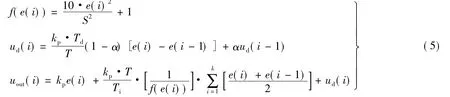
式中,kp,Ti,Td依次为比例系数、积分和微分时间常数;T为采样时间;ud(i)为引入的不完全微分调节项;α为引入的不完全微分调节系数,0<α<1;uout(i)为输出控制量.
3 被测轴的转矩常数KT的标定
由式(4)可知,位标器3个轴的转矩常数对静不平衡量及静不平衡位置测试的精度影响较大,并且对于不同的被测轴还存在个体差异,所以在对被测轴测量之前均需要先对其转矩常数按图6所示方法进行标定处理,具体步骤如下:
1)调节转台转动到任意设定角位置锁定,确定其定位良好后使其回到初始基准零位锁定.
2)安装被测轴使之与转台水平轴平行,记录被测轴转动的初始基准零位并用砝码对其配平.
3)驱动经过用砝码进行静不平衡量配平之后的被测轴匀速转动,测控系统实时采集并记录被测轴的角位移信号和驱动电流信号,处理后得到被测轴转动的角位置和驱动电流值.

图6 被测轴转矩常数标定示意图
4)判断被测轴匀速运动时驱动电流大小是否有变化,如果有变化,则返回步骤2),否则进入步骤5).
5)调整水平轴角位置转台回到初始基准零位锁定,并使位标器被测轴转动的初始基准零位也重合于水平轴角位置转台的初始基准零位.
6)进行位标器被测轴顺时针方向的轴转矩常数测量.
去掉位标器被测轴所加的驱动电压并在其正转方向的A点挂砝码M1i,被测轴因受砝码M1i重力矩作用,转动角度θ1i后停止,如图6所示,获取此时被测轴端部零位线停止位置与其初始零位线之间的夹角θ1i的角位移量、所挂砝码的重量,最后对被测轴驱动电机供入驱动电流,并不断调节这个电流的大小,使得当被测轴端部的基准零位线运动到原来的初始位置时恰好保持静止不动,记录此时的驱动电流值为I1i,设被测轴半径为R,根据力矩平衡和电机转矩理论得出被测轴正转方向的转矩常数为

7)进行位标器被测轴逆时针方向的轴转矩常数测量.
按步骤1)~6)类似方法,在其逆时针方向的B点挂砝码M2i,设I2i表示反转方向时被测轴供入的驱动电流.此时被测轴的转矩常数为

8)获取标定之后被测轴的转矩常数为
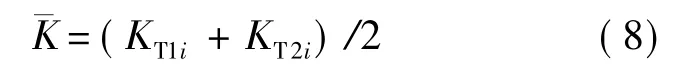
将式(8)代入式(4)可得

4 测试实验及结果分析
4.1 加载测试
在位标器模拟件外环轴端面上找到与起始零位角度为131.24°的半径位置,然后在这个半径位置上距其轴心5.10 cm处加17.66 g的质量块(这么选是因为这个位置有配重孔),即所加的静不平衡力矩大小为17.66×5.10=8.84 mN·m.然后驱动角位置转台依次锁定在预先设置的36个角位置处,再驱动位标器的被测轴以˙α=2 sin(0.50 πt)的速度进行正弦小角度振动,实时处理其监测数据并按式(9)计算每个转台锁定角位置处被测轴的静不平衡量,共得到36个静不平衡量测试数据如表1所示,第1列表示转台位置,第2列表示在该位置处的电机输出力矩均值(静不平衡力矩与其大小相等,符号相反,测试结果均保留两位小数).
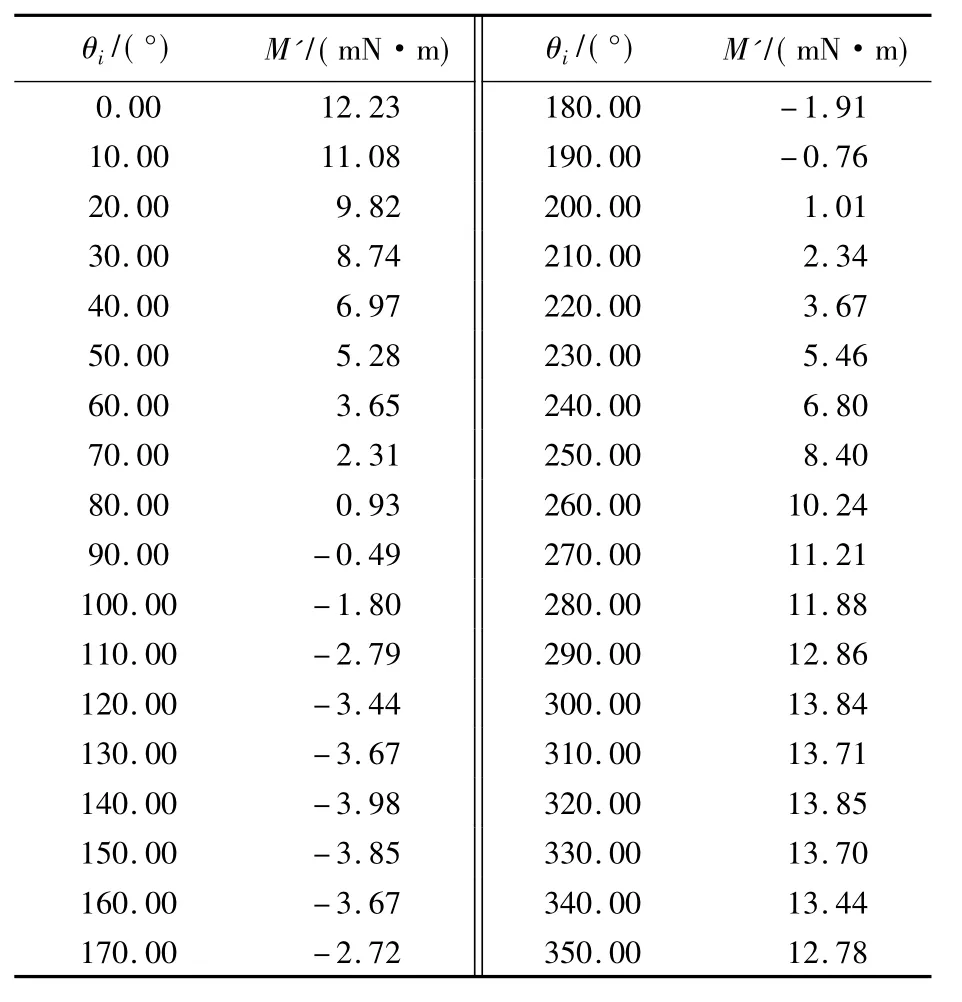
表1 在不同转台位置θi处得到的电机输出力矩M'
由表1可知,如果要直接观察得出静不平衡量(力矩)及其所处的位置很困难,所以本文采用最小二乘拟合法进行相应的求解.设所用的数据拟合曲线为

式中,自变量θi为转台所处的角位置,(°);b为静不平衡力矩所处的相位,(°);K1为静不平衡力矩的峰值,mN·m;K2为干扰力矩,mN·m;为转台所处的角位置θi处被测轴的静不平衡力矩拟合量,mN·m.
把表1中的测试数据代入式(10)求解得

图7绘出了被测轴实测的静不平衡力矩量Mθi及通过式(11)拟合得到的值,δ为其拟合的残差曲线.从式(11)及图7可以看出,拟合的静不平衡力矩值为9.04 mN·m,与实际加载只有0.20 mN·m的偏差;相位测试值为129.80°,与实际加载只有1.44°的偏差,由此可说明本文加载测试的精度非常高.
4.2 重复性测试
重复性测试实验中,实际附加的静不平衡力矩大小为10.20 mN·m,附加位置同前,即相位为131.24°.在该条件下,重复进行5次静不平衡测试,得到如表2所示的结果,其中前3次测试均为测试36个点之后进行曲线拟合求出的结果;第4与第5次测试,中途停止,共用了18个测试点.

图7 陀螺位标器静平衡测试数据

表2 静不平衡重复性测试实验
从表2中可以看出,位标器静不平衡测试重复性很高,完全满足项目的技术要求(项目要求静不平衡量大小测试精度±0.785 04 mN·m,位置测试精度±6°),并且拟合所用的算法精度也非常高,在未完成所有预设位置测试的情况下,测试结果精度也足以满足项目的要求.经过反复的重复性测试,证实该系统可以在测试最少6个点(间隔角度为10°时)的情况下拟合出较好的曲线,从而得出静不平衡力矩及其相位,且能够满足精度要求,所以系统的测试时间不会很长.
5 结论
研制了一种位标器陀螺转轴静平衡测试系统,该测试系统具有如下优点:
1)使用多功能、高精度的数据采集卡,保证了测控系统不但能快速测得陀螺位标器各个轴运动的监测量,而且具有较高的测试精度.
2)使用多功能数据采集卡自带的4个定时器输出口中的3个输出PWM信号,通过I/O口输出方向、起停信号用于陀螺位标器各个轴电机的伺服控制,极大地降低了软硬件设计的难度.
3)该测试系统操作简单,不会造成被测的位标器污损;对测试环境要求不高,适应性好,测试效率容易提高.
本文所研究的位标器转轴静平衡测试系统为其3轴平衡和配重提供了技术方法.而且该种方法也可用于测试其他已经装配好的机械转子设备的静不平衡,具有很高的工程应用价值.
References)
[1]郭晋峰,糜长军,田蔚风,等.静电陀螺转子偏心摆动造成的静电干扰力矩[J].哈尔滨工程大学学报,2007,28(6):673-677
Guo Jinfeng,Mi Changjun,Tian Weifeng,et al.Electrostatic torques coming of the rotor’s off-center spinning in ESG[J].Journal of Harbin Engineering University,2007,28(6):673-677(in Chinese)
[2]Wang H G,Williams T C.Strategic inertial navigation systems:high-accuracy inertially stabilized platforms for hostile environments[J].IEEE Control Systems,2008,28(1):65-85
[3]朱华征,范大鹏,张文博,等.质量不平衡力矩对导引头伺服机构性能影响分析[J].红外与激光工程,2009,38(5):767-773
Zhu Huazheng,Fan Dapeng,Zhang Wenbo,et al.Influence analysis of the mass imbalance torque on the performance of seeker servo mechanism[J].Infrared and Laser Engineering,2009,38(5):767-773(in Chinese)
[4]郝久玉,李惠敏.新型智能静平衡测试分选仪[J].电子测量与仪器学报,1997,11(3):44-48
Hao Jiuyu,Li Huimin.A new intelligent static balance test-classifier[J].Journal of Electronic Measurement and Instrument,1997,11(3):44-48(in Chinese)
[5]李丙乐,王厚生,王晖,等.陀螺转子的称重静平衡实验研究[J].工程设计学报,2006,13(5):332-336,341
Li Bingle,Wang Housheng,Wang Hui,et al.Experimental research of measuring static balance of gyro rotor through weighing[J].Journal of Engineering Design,2006,13(5):332-336,341(in Chinese)
[6]Liu X M,Zhao T L.Cost-effective inventory control in a valueadded manufacturing system[J].European Journal of Operational Research,2009,196(2):534-543
[7]Ra W S,Whang I H,Ahn J Y.Robust horizontal line-of-sight rate estimator for sea skimming anti-ship missile with two-axis gimbaled seeker[J].IEE Proceedings:Radar,Sonar and Navigation,2005,152(1):9-15
[8]王洪福,郑昌健,吴晓峰,等.高精度稳像平台静平衡测量系统设计[J].红外与激光工程,2012,41(6):1618-1622
Wang Hongfu,Zheng Changjian,Wu Xiaofeng,et al.Design of ultra precision static balance testing system for video-stabilization gimbals[J].Infrared and Laser Engineering,2012,41(6):1618-1622(in Chinese)
[9]Masten M K.Inertially stabilized platform for optical imaging systems:tracking dynamic targets with mobile sensors[J].IEEE Control Systems Magazine,2008,28(1):47-64
[10]Jing J P,Meng G,Sun Y,et al.On the non-linear dynamic behavior of a rotor-bearing system[J].Journal of Sound and Vibration,2004,274(3):1031-1044
[11]Rodrigues D J,Champneys A R,Friswell M I,et al.Experimental investigation of a single-plane automatic balancing mechanism for a rigid rotor[J].Journal of Sound and Vibration,2011,330(3):385-403
[12]Tiwari R,Chakravarthy V.Simultaneous estimation of the residual unbalance and bearing dynamic parameters from the experimental data in a rotor-bearing system[J].Mechanism and Machine Theory,2009,44(4):792-812
[13]Wang L G,Cao D Q,Huang W H.Nonlinear coupled dynamics of flexible blade-rotor-bearing systems[J].Tribology International,2010,43(4):759-778

