主操作手重力补偿下的时延控制
王宏民, 吕雄飞, 王茂生, 苏凤武, 康红明
(1.黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022;2.黑龙江建筑职业技术学院 机电工程技术学院, 哈尔滨 150025)
主操作手重力补偿下的时延控制
王宏民1,吕雄飞1,王茂生2,苏凤武1,康红明1
(1.黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022;2.黑龙江建筑职业技术学院 机电工程技术学院, 哈尔滨 150025)
针对自主研制的应用于外科手术的三维力反馈型主操作手的重力补偿问题,对主操作端控制中产生的时延进行深入分析,利用多线程、多事件技术尽可能降低主操作端的时间时延。通过矢量分析的方法得到电机为平衡位置机构静力平衡所需的输出力矩。分别在ADMAS和MATLAB环境下,进行仿真对比分析。仿真结果验证了建立的系统动力学模型的正确性。该重力补偿方法可以满足主操作手的重力平衡要求。
主端机器人; 重力平衡; 时延控制; 外科手术
0 引 言
近年来,随着外科手术机器人技术的发展,众多学者研究主操作手作为系统中的力反馈设备在重力补偿方面,取得了一定的成果。Nathan和Herve利用配重方法对串联机构实现重力补偿[1-2]。Streit利用弹簧对连杆机构进行重力补偿[3]。Kumar利用滑轮实现机构的重力补偿[4]。Kazerooni等利用直接驱动的方法对并联机构进行重力补偿[5]。上述文献大多采用机械的方法来补偿精度不高的问题。笔者将对主操作端控制过程中产生的时延进行分析,利用多线程、多事件技术尽可能降低主操作端的时间延时,通过矢量分析方法建立系统静力学模型,计算各部分重心在关节空间中所产生的转矩,利用力矩电机输出相应的转矩进行重力补偿。
1 主操作端时延特性分析
主操作端时延主要包括对主操作手的位姿信息采集和电机控制所用的时间。由于主操作手需要完成的重要工作是在手术过程中时刻保持重力平衡的,所以重力补偿程序启动后,主操作手才进行力反馈算法的执行。主操作手端控制系统的流程如图1所示。

图1 主操作手控制系统流程

图2 主操作手耗时
从图1可以看出,完成一次重力补偿需要三个过程,即开启重力补偿—执行—开启力反馈算法。图2是重力补偿周期tz和信息显示耗时th示意。从图2a可以看出,主操作端的重力补偿周期在90 ms左右。主操作手除了重力补偿之外,还有对主手位姿、反馈力等信息的显示。图2b中经过测量耗时为10 ms左右。因此,可知主手端的采样周期总体平均耗时100.63 ms。
2 多线程、多事件技术的时延控制
主操作手采用多线程技术[6],将重力补偿线程的结束作为一个事件,只有等到该事件触发后,才进入数据发送线程和信息显示线程。当重力补偿线程得到位姿和电流信息之后,通知另外两个线程进行相应的操作。然后,重力补偿线程继续进行重力补偿的计算,将电流值发送给三个驱动器,保证主操作端的重力平衡。数据发送周期ts如图3所示。从图3中可以看出,多线程单事件驱动的数据发送周期均值为94.587 ms。
多线程技术使主端时延相比于100.63 ms的采样周期略有减小,但时延依然很大。在保证重力补偿的方法的基础上,采用多事件技术,在发送一次电流指令之后进行一次位置采样,然后触发数据发送线程。多事件数据发送周期td如图4所示。从图4可以看出,基于多事件技术的主操作端的采样周期均值为36.5 ms,大幅降低了主操作端的采样周期。

图3 多线程数据发送周期

图4 多事件采样周期
3 主操作手静力学分析
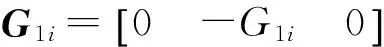




G1ix=G1i·bix=-G1i2xbi,
G1iy=G1i·biy=-G1i2ybi,
G1iz=G1i·biz=O,



图5 上连杆受力分析
图6是对半圆盘几何中心的分析。根据矢量分析的方法[7],建立上连杆BiCi的力和力矩平衡方程
∑Mx(F)=MBicosγi+MCicosγi+

∑My(F)=MBicosβi+MCicosβi=0,
∑Mz(F)=MBicosφi+MCicosφi-

式中:MBi——主动关节在被动关节产生的力矩;
MCi——动平台在在被动关节产生的力矩;
γi、βi、φi——MCi(MBi)分别和Bi-xBiyBizBi坐标系中各轴的夹角。

G2ix=G2i·aix=-G2i2xai,
G2iy=G2i·aiy=-G2i2yai,
G2iz=G2i·aiz=-G2i2zai,



(-FCiy-G1iy)·(2xai2ybi+3xai3ybi)。
根据力矩平衡原理,并考虑半圆盘几何中心的分布如图7所示,可得zai轴方向的力矩表达式

|AiNi|cos(∠BiAiNi)-G2iy·
|AiNi|sin(∠BiAiNi)=0,
(6)
式中:∠BiAiNi=33°;
|AiNi|=0.026 9 m。

图6 下连杆受力分析






图7 半圆盘几何中心分析
4 实验验证
图8为沿x轴方向的运动轨迹。图8a参数的运动轨迹为沿x轴方向,范围为-50~50 mm(y=25 mm,z=200 mm),F=(-4.9 N,-4.9 N,-4.9 N)。图8b、c分别给出了每个驱动轴的力矩M1、M2和M3的ADMAS仿真结果和力学模型理论值。通过两种方法下的误差对比可以得出,两种方法结果基本一致,力矩误差Me对比如图8d所示,误差对比如图8d所示。
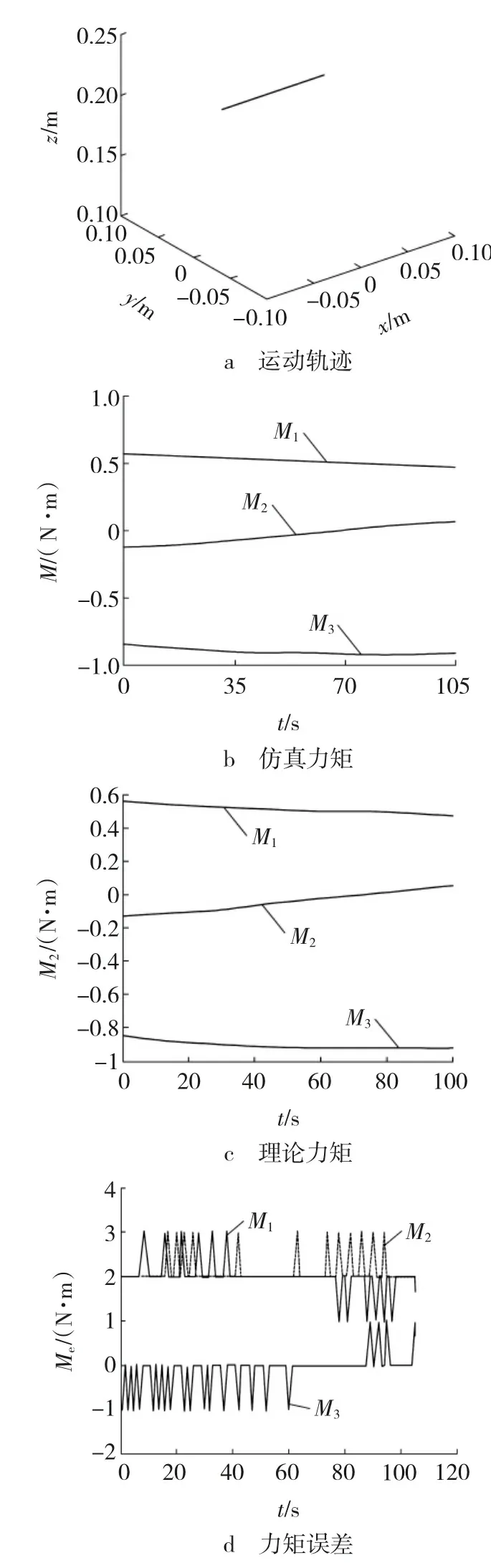
图8 x轴方向运动轨迹
5 结束语
笔者对自主研制的可用于外科手术的主操作手重力补偿算法进行了研究。通过矢量分析的方法建立系统动力学模型,计算各部分重心在关节空间中所产生的转矩,并利用力矩电机输出相应的力矩进行重力补偿。通过仿真实验表明,重力补偿方法控制效果令人满意,主操作手可以实现任意位置静平衡,提高了操作性能,能够保证手术的安全性。
[1]NATHAN R R. A constant force generation mechanism[J]. ASME Journal of Mechanism, Transmissions and Automation in Design, 1985, 107(4): 508-512.
[2]HERVE J M. Device for counter-balancing the forces due to gravity in a robot arm[J].United States Patent, 1986, 14(3): 620-623.
[3]STREIT D A, GILMORE B J. Perfect spring equilibrator for rotatable bodies[J]. ASME Journal of Mechanisms, Transmissions and Automation in Design, 1989, 11(4): 451-458.
[4]ULRICH N, KUMAR V. Passive mechanical gravity compensation for robot manipulators[C]//Proceedings of the IEEE International Conference on Robotics and Automation. California: Sacramento, 1991: 1536-1541.
[5]KAZEROONI H, KIM S. A new architecture for direct drive robot[C]//Proceedings of the ASME Mechanism Conference. Chicago:[s.n.], 1990: 21-28.
[6]TOMONORI YAMAMOTO. Applying tissue models in teleported robot-assisted surgery[D]. Baltimore: The Johns Hopkins University, 2011.
[7]赵枝凯. 机器人辅助远程骨科手术时延控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
[8]HU B, YU JJ, LU Y, et al. Statics and stiffness model of serial-parallel manipulator formed by k parallel manipulators connected in series[J]. Journal of Mechanisms and Robotics-Transactions of The ASME, 2012, 4(3): 123-136.
[9]YU L, SONG H, WANG T, et al. A new asymmetrical mass distribution method on the analysis of universal “force-sensing” model for 3-DOF translational parallel manipulator[J]. Industrial Robot: An International Journal, 2014, 41(1): 56-69.
(编辑徐岩)
Time delay control with gravity compensation for master manipulator
WANGHongmin1,LÜXiongfei1,WANGMaosheng2,SUFengwu1,KANGHongming1
(1.School of Electrical & Control Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China; 2.College of Mechanical & Electrical Engineering Technology, Heilongjiang College of Construction, Harbin 150025, China)
This paper proposes a gravity compensation algorithm for three-dimensional force feedback manipulator, a self-designed approach used in surgical operation. The paper provides an in-depth analysis of time delay occurring in master operation control system and introduces the greatest reduction in time delay occurring master control system using multi-thread and multi-event technology and a solution to the motor output torque for balancing the master gravity using vector analysis method. The simulation analysis conducted in ADMAS and MATLAB environment verifies the viability of system dynamics model and the method is adequate for gravity balance.
master manipulator; gravity compensation; time delay; surgical operation
2013-12-11
黑龙江省教育厅科学技术研究项目(12541713;12541723)
王宏民(1978-),男,河北省承德人,副教授,硕士,研究方向:自动控制、机器人控制,E-mail:wang-hongmin@163.com。
10.3969/j.issn.2095-7262.2014.03.011
TN953
2095-7262(2014)03-0272-05
A

