一类具有投资和干扰的Poisson-Geometric风险模型
杨善兵
(盐城工学院 基础教学部,江苏盐城 224051)
1 模型介绍
定义1.1 如果某随机变量N对应的概率母函数为

则称母函数G(t)所对应的分布为复合Poisson-Geometric分布,记为PG(λ,ρ)。之所以称为复合Poisson-Geometric分布是因为可以用以下方法得到该分布:

Poisson分布的一个重要性质是方差等于均值,但是实际上索赔次数并不完全遵循Poisson分布规律,方差往往大于均值,这种现象对于Poisson分布来说叫散度偏大,散度偏大的模型有很多,其中复合Poisson-Geometric过程就是一例,本文就是介绍一类保费是随机收取的复合Poisson-Geometric风险模型。
考虑盈余过程[1-5]

其中:u(u≥0)为初始准备金,i(i≥0)为投资利率,σ是常数,W(t)是标准布朗运动,表示公司的随机干扰,N(t)是强度为λ1时齐的Poisson过程。随机变量Xi是收取的保费,设数学期望为μX;随机变量列{Yi,i=1,2,…}是独立同分布的索赔随机变量列,设数学期望为μY。索赔计数过程K(t)是参数为(λ2,ρ)(0≤ρ<1)的 Poisson-Geometric过程,再设{Xi,i≥1},{Yi,i≥1},{N(t),t≥0},{K(t),t≥0}和{W(t),t≥0},相互独立。
通篇论文假定所有随机变量的分布函数是轻尾的,数学期望为有限,且二阶矩存在。为保证保险公司稳定经营,需进一步假设λμ >,1X即表示单位时间内保费收入大于索赔,由此定义安全负荷系数θ=-1。定义破产时T=inf{t≥0:S(t)<0|S(0)=u},如果上集合不存在,则破产时T=∞;最终破产概率为Ψ(u)=Pr(T<∞|S(0)=u),则生存概率为Φ(u)=1-Ψ(u)。
2 最终破产概率

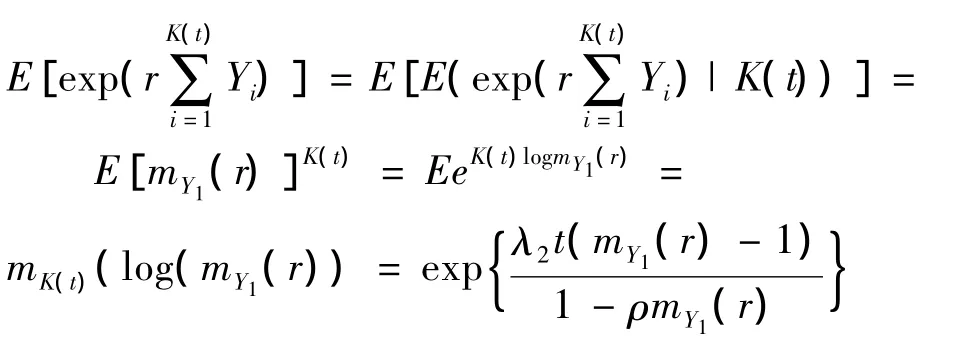
上面的第5个等式应用到引理1的结论。
于是有
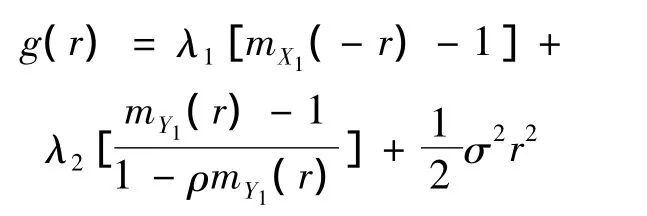
引理3 方程g(r)=0,在r>0时,有唯一的正解R,并称此解R为调节系数。证明:由引理2知:

设{Ft,t≥0}是由过程 N(t)、K(t)和 W(t)生成的最大σ-代数流,显然是非降的σ-代数流。
引理4 过程{Q(t),t≥0}是平稳的独立增量过程。
证明:证明过程见参考文献[3]。
引理 5 {Rt,Ft,t≥0}是一鞅,其中 Rt=exp(-R(u(1+i)+Q(t))),R为调节系数。
证明:(1)显然 Rt是关于{Ft,t≥0}可测的;
(2)由引理3得到
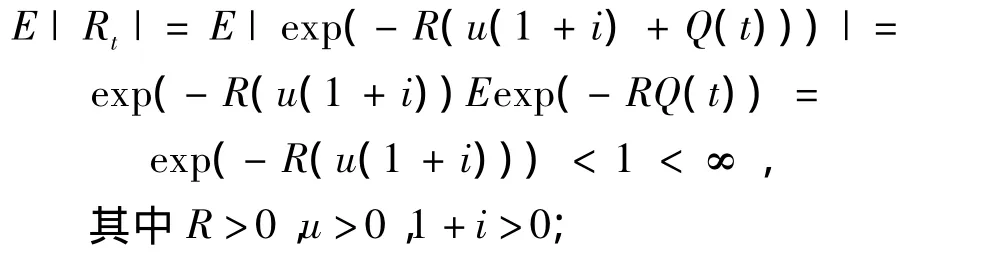
(3)对任意 0≤v≤t,

对于固定的时间 t,可以证明 T∧t是关于{Ft,t≥0}的有界停时。
定理:模型(1)的最终破产概率为

证明:利用有界停时定理:
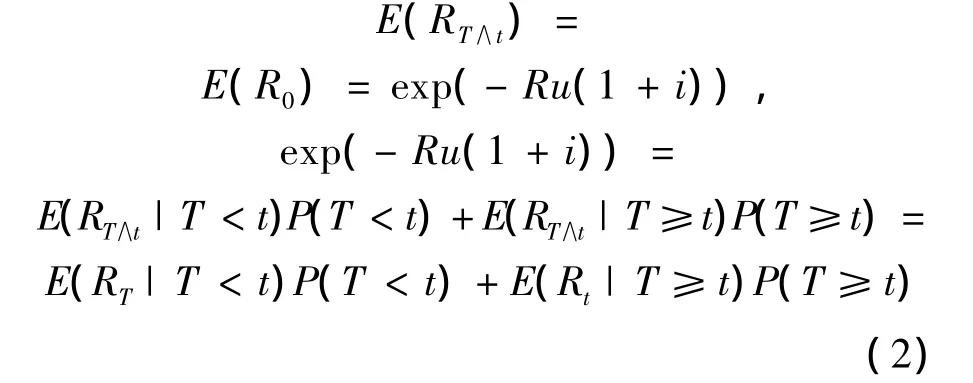
由于当 t<T 时,S(t)>0,又{Rt,t≥0}是非负的鞅,由强大数定理知S(t)=+ ∞,a.s.,再由单调收敛定理和勒贝格控制收敛定理得到

推论:最终破产概率Ψ(u)满足林德伯格不等式,即Ψ(u)≤exp(-Ru(1+i))。
证明:由于调节系数 R>0,S(T)≤0,exp{-RS(T)}≥1,不等式成立。
该不等式说明本文所构造的模型的最终破产概率的上界也是关于初始准备金u的指数函数,同时模型(1)具有和文献[4]所讨论的模型类似的结论。
[1]熊双平.索赔次数为复合Poisson-Geometric过程的常利率风险模型[J].经济数学,2006,23(1):15-17.
[2]熊双平.索赔次数为复合Poisson-Geometric过程的常利率风险模型的罚金函数[J].经济数学,2008,25(2):136-142.
[3]毛泽春,刘锦萼.索赔次数为复合Poisson-Geometric过程的风险模型及破产概率[J].应用数学学报,2005,26(3):419-428.
[4]杨善兵,杨牧原.具有干扰和固定投资的相依聚集索赔的风险模型[J].合肥学院学报,2012(4):8-10.
[5]熊双平.带干扰的索赔次数为复合Poisson-Geometric过程的负风险和模型[J].经济数学,2007,24(1):37-41.

