高超声速飞行器结构热气动弹性优化设计
余胜东,马金玉
(温州职业技术学院电气电子工程系,浙江温州 325035)
高超声速飞行器指的是一种飞行马赫数超过5倍音速的飞行器,主要活动空间为大气层和跨大气层,具有巨大的经济价值和军事价值。随着材料科学与设计方法的进步,高超声速飞行器的设计向着新型轻质复合材料、升力体和大型薄壁结构方向发展,并由此带来了一系列气动弹性问题[1]:结构固有振动频率降低,弹体模态与刚性模态相互耦合,加之高速高温下强烈的热效应影响,结构与空气动力学耦合问题更为复杂。国内外多项研究表明,进行热气动弹性剪裁设计可以大大改善高超声速飞行器气动弹性特性,提高颤振速度。
气动弹性剪裁设计一般是指考虑颤振、发散、固有频率、变形、副翼效率、强度和飞行载荷等多种约束条件,对整架飞机或单独机翼进行的复合材料优化。和一般的结构优化相比,气动弹性剪裁设计具有研究对象复杂、计算耗费大、涉及学科多、设计变量多、约束条件多且复杂等特点,在热气动弹性优化设计中尤为突出。
本文参考X-43外形尺寸,构建全机有限元热模型,充分利用FD ISIGHT多学科优化平台自身优化功能,对MSC.Nastran与MATLAB进行集成,保持全机结构、重量不变的情况下,以蒙皮铺层角度和铺层顺序为设计变量,以机翼非线性颤振速度为优化目标,实现了对高超声速飞行器结构的热气动弹性优化设计。结果表明复合材料层合板的铺层角度和铺层顺序对飞行器颤振速度有一定影响。
1 理论基础
1.1 模型气动力计算
活塞理论[2]的基本假设是在高马赫数飞行条件下,且翼剖面厚度很薄可以忽略,因此翼面上某一点的扰动对其他点所产生的影响是很弱的,忽略这种微弱效应,合理假设翼型上某一点的压力仅与此点的下洗速度有关,且可以形象的描述为:当活塞置于圆形管道中运动时,其所受到的压力大小只与其运动速度有关。活塞理论气动力精确表达式:

三阶近似表达式为:

假设x为顺气流方向,则下洗速度为:

1.2 热气动弹性计算
参考焓[3]方法,又称作参考温度法,其主要思路是考虑流经飞行器表面的气流,假设不可压缩气流的温度升高至一个给定的参考温度值T*,同时对不可压缩气流中的一些随着温度变化而变化的量,比如(μ,ρ),务必使用此温度值T*来表示。其中将参考温度T*代入计算得到的参数用“*”标示于右上角以示其与参考温度T*有关,则飞行器表面任一点的τω等价于相应的可压流的τω。假设可以得到T*的值,即可以通过对不可压流摩阻公式的求解来得到可压流中相关参数,其摩阻表达式为:

其中:
T*表示飞行器表面温度;
T∞=表示边界层外缘温度,由气动力计算部分参数可以得到;
Tr为恢复温度。
通常机翼前缘部分受到的气动加热现象最为明显,其前缘部分和翼面部分可以忽略厚度因素看作平板[4]来进行计算。相应的热流密度也可以用平板模型的公式来表示。
参考粘性系数μ*通过萨特兰表达式求解得出:

在气动加热[5]条件下,结构主要受到两个方面的作用而发生改变,一方面是结构材料本身的性质在高温环境中会呈现不同的特性,另一方面是整个结构在高温作用下,结构内部有热应力作用而使结构的特性发生改变。其中材料本身在温度场影响下,与温度相联系的两个参数弹性模量E和泊松比μ均会发生改变;而结构整体上的特性改变是因为热应力的产生使得结构有膨胀趋势,而此时结构受到来自内部和外部的约束作用,结构的有效刚度产生了改变,相应的振动特性也发生了改变。有效刚度[6]的改变通常可以具体描述为结构软化效应或硬化效应,这种效应在梁结构或者板壳结构上反应更为突出。
令结构初始单元线性刚度矩阵为K0,受热应力作用生成的多余刚度为Kσ,则结构受热效应作用后总的应力刚度矩阵等效为:

则在热效应作用下的结构振动表达式为:

式中,M表示质量矩阵,φ表示振型,φ为振频。
此时的动力学方程即描述了结构在热载荷作用下结构振动特性,即简化为求上式的广义特征值问题。以p-k法为例,颤振方程[7]为:

其中无量纲算子:

通过颤振方程的求解,确定g随V的变化,当g=0时,对应的速度即为颤振速度VF。颤振约束可以定义为

表示第i阶振动在V下的阻尼小于零,即未达到颤振临界状态。
1.3 热气动弹性优化设计
热气动弹性优化设计[8]是一个交叉学科问题,主要涉及3个部分的有关理论:复合材料力学、热气动弹性计算、优化方法。热气动弹性优化设计从本质上来说是结构优化设计方法[9],通过对复合材料的铺层角度和铺层顺序的改变,合理配置复合材料结构的刚度,充分发挥复合材料机翼的弯扭耦合效应,在满足强度、装配、刚度、制造、稳定性等设计要求的同时,使机翼在气动载荷的作用下产生有利于抑制颤振、提高发散速度、改善操作性能和气动稳定性能、提高机动性能的弹性变形,进而改善飞行品质。
2 数值计算与分析
2.1 模型描述
构建以高超声速飞行器X-43的外形轮廓尺寸(见图1)[10]为基础的高超声速飞行器全机模型(见图2),其机身及平尾部分结构主要由骨架和蒙皮组成,钝头体头部为实体结构,其中最易发生颤振的平尾部分与机身由转轴相连,同时,机身和发动机采用一体化布局设计。在此基础上加上热防护结构建立气动热模型[11],即辐射屏蔽层和绝热层。其中辐射屏蔽层为PM-2000蜂窝夹层,厚度为2 mm;绝热层是绝热结构,厚度为8 mm。环境温度300 K,辐射层发射率为0.7,边界条件为绝热。
2.2 模型气动热计算

图1 X-43结构尺寸图Fig.1 The X-43 vehicle configuration

图2 X-43有限元热模型Fig.2 Finite element model
对类X-43高超声速飞行器模型进行气动热计算[12],得到热流场分布和结构温度场分布。其中使用MATLAB编程实现用等效温度法计算模型表面受到的热流场分布,沿着机身x方向将机身分成20等份,假设每份所处的热流密度一定,则热流场为20个不相互连续的离散温度值构成,在初始环境温度为300 K时,计算得到的热流场分布如图3所示,由该图得到热流密度沿机身x 向从127935 J/(m2·s)到43000 J/(m2·s)逐渐降低,飞机头部所受热流量最大。

图3 热流场分布曲线Fig.3 The heat flow field
根据算出的热流密度场,在 MSC.Patran[9]中将其加载在有限元模型表面,同时加上环境热辐射值加以平衡,通过 MSC.Nastran求解序列SOL153对其进行温度分布计算。其有限元模型的热防护层外表面稳态温度场分布如图4所示。由图可得,飞行器头部、垂尾与平尾外表面温度最高,约为2000 K,机身温度相对低一些,约为950 K:

图4 外表面稳态温度场分布Fig.4 The temperature field on surface
经过辐射屏蔽层和绝热层的热防护作用,飞行器复合材料蒙皮层的稳态温度分布[13]如图5所示。由图可得,经过隔热作用,复合材料蒙皮的温度被大大降低了,其中机身温度基本在400 K左右,局部最高温度为480 K。

图5 隔热后蒙皮稳态温度分布图Fig.5 The temperature field after heat insulation
2.3 高超声速热颤振计算
采用三阶活塞理论计算高超声速非定常气动力,并用p-k法[14]进行颤振计算。由计算结果可知,发生颤振的形式为平尾翼面扭转和挥舞的耦合,颤振马赫数是4.16,颤振频率是287.5 Hz。计算得到的颤振V-g、V-ω图如图6所示。
2.4 模型优化

图6 考虑热效应状态下颤振计算结果Fig.6 The flutter result with heat effect
为了满足机翼气动弹性设计要求,提高颤振速度,以FD ISIGHT软件[15]为平台对此高超声速飞行器热模型进行结构热气动弹性优化设计。首先在包含模型信息的输入文件中选定设计变量为复合材料蒙皮的铺层角度和铺层顺序,设置蒙皮铺设厚度为8层对称铺设,每层厚度为0.25 mm,初始铺层顺序为[90°/45°/0°/-45°];其次利用本文所提出的高超声速飞行器热颤振速度求解方法计算全机的颤振临界速度;最后,判断所得计算结果是否满足优化目标所设定的飞行器颤振速度值,满足则结束优化程序,输出最优结果,不满足则通过优化算法[16](多岛遗传算法),修改输入文件中设计变量的值继续进行优化计算。优化流程如图7所示。

图7 FD ISIGHT优化流程图Fig.7 Optimization flow-process on FD ISIGHT
经过多次迭代计算后,得到颤振V-g和V-ω曲线如图8所示。
优化后的铺层顺序为[0°/45°/-45°/90°],临界颤振马赫数为6.12,颤振频率是345.7 Hz。优化后的各阶频率均呈现出不同程度的上升趋势,特别是平尾的扭转频率有着较大的提高。优化结果表明优化后的铺层角度和铺层顺序能有效的增加结构的刚度,延迟颤振现象的发生。
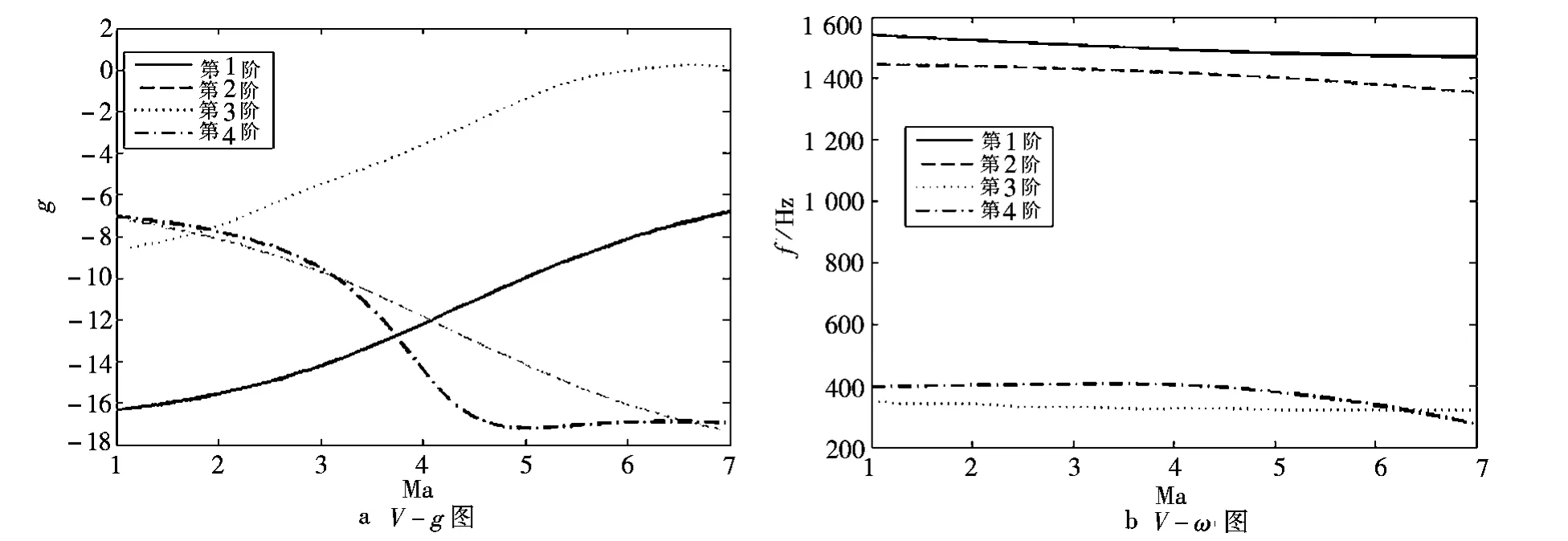
图8 优化后颤振计算结果Fig.8 The flutter result after optimization
3 结论
本文首先根据相关资料建立了高超声速飞行器的全机热结构有限元模型,随后提出了一种考虑热效应的颤振计算方法,最后结合FD ISIGHT软件的优化功能,选用多岛遗传算法对全机模型的复合材料蒙皮的铺层角度和铺层顺序进行了气动弹性优化设计。优化结果表明,复合材料蒙皮的铺层角度和铺层顺序对飞机的气动弹性性能的改善有比较大的影响,采用本文所述的方法能有效的改善高超声速飞行器的气动弹性性能,具有较好的工程应用价值。
[1]陈桂彬,邹丛青,杨超.气动弹性设计基础[M].北京:北京航空航天大学出版社,2004.10.
[2]张伟伟,叶正寅.基于当地流活塞理论的气动弹性计算方法研究[J].力学学报,2005,37(5):632-639.
[3]Norris G.Boeing studies X-43 evolved crew derivative[J/OL].(2011-10-07)[2014-03-10].http:www.aviationweek.com/aw/generic/story_generic.jsp?channel=aerospacedaily&id=news/asd/2011/10/06/01.xml&headline=Boeing Studies X-43 Evolved Crew Derivative.
[4]Walker S,Rodgers F,Falcon hypersonic technology overview,AIAA-2005-3253[R].NewYork:AIAA,2005.
[5]Wu Z G,Yang C.Flight loads and dynamics of flexible air vehicles[J].Chinese Journal of Aeronautics,2004,17(1):17-22.
[6]Anderson J D.Hypersonic and high-temperature gas dynamics[M].2nd ed.New York:Mcgraw-Hill College Publication,1946,25(3):247-251.
[7]杨炳渊.颤振的工程计算方法[M].北京:宇航出版社,1993:412-430.
[8]Hirschel E H.Selected aerothermodynamic design problems of hypersonic flight vehicles[M].Berlin Heidelberg:Springer-Verlag,2009:1-10.
[9]Rodden W P,Johnson E H.MSC/NASTRAN Version 68 Aeroelastic Analysis Users Guide[M].New York:The MacNeal-Schwendler Corporation,1994.
[10]Valentina B,Kaloyanova,Karman Netal.Structural modeling and optimization of the joined wing of a high-altitude long-endurance(HALE)Aircraft,AIAA-2005-1087[R].NewYork:AIAA,2005.
[11]Razani R.The behavior of the fully stressed design of structures and its relationship to minimum weight design[J].AIAA,1965,3(12):2262-2268.
[12]Chang C S,Dewey H H,Mayuresh J P.Flight dynamics of highly flexible aircraft[J].Aircraft,2008,45:538-545.
[13]Xie C C,Leng J Z,Yang C.Geometrical nonlinear aeroelastic stability analysis of a composite high-aspect-ratio wing[J].Shock Vib,2008,15:325-333.
[14]Arizono H,Isogai K.Application of genetic algorithm for aeroelastic tailoring of a cranked arrow wing[J].Journal of aircraft.2005,42(2):493-499.
[15]牟淑志,杜春江,牟福远,等.基于多岛遗传算法的连续体结构拓扑优化[J].机械科学与技术,2009,28(10):1316-1320.
[16]黄平,孟永钢.最优化理论与方法[M].北京:清华大学出版社,2009.

