Darrieus型垂直轴风力机气动特性研究∗

史瑞静，李凤婷，樊小朝，王维庆

(新疆大学电气工程学院，教育部可再生能源发电与并网控制工程技术研究中心，新疆乌鲁木齐830047)

0 引言

由于垂直轴风力机自身的特性，相对于水平轴风力机，人们对它们的使用越来越感兴趣.垂直轴风力机直接与发动机的底部位置相连，设计简单，并且结合最简单的控制策略，该策略不需要任何的变桨或偏航机构，在城市和非常偏僻地区都可以建设，不管在哪所需维护的工作量都是最小的.另一方面，由于垂直轴风力机特有的非稳态工作条件，其特点是空气动力学的复杂性.因此，必须要有灵活和可靠的设计方案，这些方案是得到实验数据的预先验证的[1,2].

研究表明，关于垂直轴风力机的复杂的空气动力特性的模拟，已经建立了不同的数值模型，目前主要有三种数值模型.第一种模型是Strickland的“多重流管”模型，后来Paraschivoiu考虑“双盘”的改进模型，该模型具有的优势是能快速估计整个功率曲线，并且完成生产设计，但另一方面，结果的可靠性依赖于所采用的气动数据库的质量和扩展度[3].第二种模型是对达里厄涡改进的尾涡模型，是一种关于空气动力特性的新的见解，在另一方面，相对于前面提到的方法，此模型所需的仿真计算时间明显的增加[4].第三种计算流体动力学（CFD）能够最准确的描述风力机的空气动力特性，但是，在另一方面，也需要更多的计算时间，这限制其用于最终测试运行仿真及对风机的设计[5−7].

1 物理模型

在“双重流管”模型中，双驱动转盘分为逆风和顺风转子，其中诱导因子（感应系数）表示由于自由流与叶片相互作用的气流速度的变化率，定义式为

其中va表示空气自由流速度，vb表示叶片气流速度.

感应系数等同于翼型叶片上的力产生的动量的变化，为了得到简单可靠的收敛模型，提出了逆风时的瞬时流向力之间的方程式[8]

通过叶素理论可以得到类似的公式

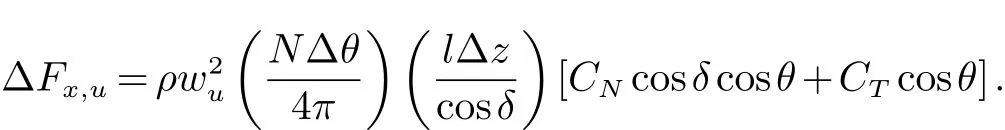
其中ρ表示空气密度，r表示叶片半径，∆θ表示方位角网格尺寸，∆z表示高度网格尺寸，θ表示方位角，vu,wu分别是当地的风速和逆风向时叶片的相对速度，N为叶片的数目，l是弦长，δ是叶片局部斜率，CN和CT分别为法向和切向气动力系数，CN和CT公式由空气动力学系数导出

其中α表示攻角.

类似地可以导出顺风时的诱导因子，可以清楚地看出，空气动力系数在对性能估计的迭代求解中有重要作用，对它们的选取应特别注意.特别的，由于不同相对速度引起的运行情况，使得雷诺数在较大范围内变化.为了从空气动力学的数据库获得最可靠的估计，攻角和雷诺数通过插值法选取，该插值算法是采用分段三次埃尔米特插值多项式算法（Piecewise Cubic Hermite Interpolating Polynomial：PCHIP），可以得到更平滑的内插，比样条内插法要好.

对风力机动态失速的研究，不同的研究者提出了不同的空气动力特性模型.叶片在周期性旋转变化，气动力系数不同于静态值，特别是在失速时[9].

基于CT切向气动力系数，气动转子的力矩可表示为

其中Nθ和Nv分别是方位角和垂直网格数，wi为逆、顺风向时叶片的相对速度.最后，功率和功率系数被定义为

其中ω为旋转速度，AS为转子扫掠面积.

2 垂直轴风力机的气动特性

Sheldahl等人建立了关于垂直轴风力机的BE-M模拟的数据库[10]，根据实验得到的数据库主要涵盖三种类型的机组：NACA 0009、NACA 0012和NACA 0015，雷诺数范围在3.5×105∼7×105，该数据库还可以通过数值算法依次拓展到NACA 0018、NACA 0021和NACA 0025，并且适合更大范围的雷诺数，还可以应用到定常流低雷诺数的垂直轴风力机.NACA 0012在低雷诺数时气动升力系数如图1所示.

这个数据库中图的突出特点为必须保持考虑以下的仿真结果，升力系数在失速状态的分布呈现出非常陡峭下降的趋势，攻角增加1˚或2˚，升力系数由最大值达到最小值.这是由于风机机翼边缘剖面很薄的缘故，从而导致了风机的突然失速，而且这种极端的情况，也与为了获得这些系数的数值算法的特性有关.此外，在雷诺数低于1.6×105时，在某些特定攻角下升力系数呈现负的值，这似乎与平板的相似性相违背，这主要是因为，在此数据库建立在雷诺数高于1.6×105基础之上.此外，还可以得到所有雷诺数情况下攻角大于30˚时所研究风机类型的升力系数，但NACA 0012除外，有很小的差异，NACA 0012型号风机在不同雷诺数下的升力系数如图2所示.

图1 NACA 0012低雷诺数时攻角对升力系数的影响

图2 NACA 0012型号风机在不同雷诺数下的升力系数

翼面较厚时，失速升力系数的降低分布趋势不太陡，整体情况是光滑的，另一方面，在30˚时几乎所有的升力系数都有一个跳跃，这是因为，在所有情况下数值算法中所提供的30˚这一点的数值都是一样的，数据库之间的关联不顺畅.

Paraschivoiu等人建立了关于垂直轴风力机的另外一种模拟数据库[11]，涵盖三种类型的机组：NACA 0012、NACA 0015和NACA 0018，雷诺数范围在104∼107.此数据库和上一个非常相似，但有不同迎角下大量的气动力系数，可能通过插值得到更多的不同的数据.NACA 0018在雷诺数1.6×105时的升力系数随攻角变化，Paraschivoiu和Sheldahl的插值数据库是不同的，如图3所示.

图3 NACA 0018在雷诺数1.6×105的升力系数

图4 NACA 0012在雷诺数1.6×105的升力系数

这些数值上的差异可以认为是有限的，但垂直轴风力机在此攻角范围内的运行情况有轻微的差异也是不能被忽略的.为了显示数据库的差异，将所有雷诺数的情况，甚至在某些攻角下出现负升力系数的情况，在下面研究中进行了比对.

Lazauskas等人改进了Sheldahl数据库[12,13]，对明显的异常情况进行了纠正.在Sheldahl创建的数据库中，可明显的观察到在实验数据和数值模拟预测的升力系数有一个“跳跃”.Lazauskas等人对这个值进行了修正，得到了一个光滑的曲线图，NACA 0012在雷诺数1.6×105时的升力系数如图4所示.这些文献中提到的数据库应用于攻角在±180˚之间的垂直轴风力机.另一些研究人员对同一剖面的翼型在低雷诺数下进行了实验，得到测试结果，但是攻角范围有限.攻角低于30˚时，并逐渐变小，垂直轴风力机可以运行在大多数的方位和垂直的位置，所以可以合理的假设，将攻角增大一些，数据库的有限数值扩展不会对预测结果有很大的错误影响.

Jacobs等人实验研究了NACA 009、NACA 0012、NACA 0015、NACA 0018和NACA 0021型号的风机，雷诺数范围在1.6×105∼3×107，提供了攻角28˚时的空气动力系数数据库[14].为了克服这一局限性，Sheldahl认为要创建一个完整数据库应该将更高迎角的空气动力系数包括在内.不过，为了尽量减少数据库之间的不连续性提供一个平滑的变化趋势，在数据库中包含在联接区域做小的修正.雷诺数范围在3.6×105∼107，NACA 0012、NACA 0018型风机的空气动力系数如图5-6所示，很明显Jacobs与Sheldahl在初始时都是线性变化的，但升力系数变化趋势之间有相当大的差异.另一方面，Sheldahl升力系数的特点有一个陡峭的和早期的失速状态，从最大升力以后有明显的下降.此外，Jacobs的最大升力值高于Sheldahl的，这是因为雷诺数高，和机翼厚度有关.

图5 NACA 0012型风机的空气动力系数

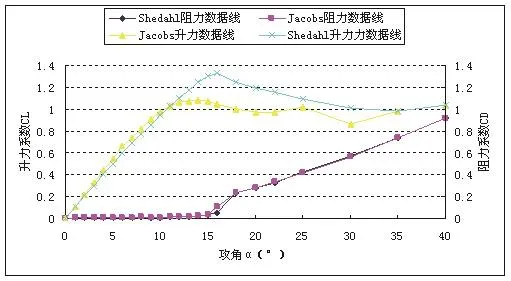
图6 NACA 0018型风机的空气动力系数

Bullivant研究了NACA 0025，雷诺数为3.2×106，攻角小于25˚，并和Shedahl的做了比较，如图7所示，Bullivant的升力和阻力系数曲线要光滑些，在研究方法（实验/数值模拟）上，提出了一个相当大的跳转链接变化，Bullivan的最大升力系数也较低，因此，具有较高的阻力系数[14].

对称剖面的SNLA0018-50是由桑迪亚国家实验室对传统的NACA 0018的改进，专门应用于垂直轴风力发电机组的研究，采用不同的转子配置.Gregorek等人实验研究了高雷诺数（＞106），攻角小于30˚的情况，并得到数据，平均雷诺数1.41×106时的空气动力系数如图8所示.

图7 NACA 0025型风机的空气动力系数

图8 SNLA0018-50型风机的空气动力系数

以上介绍的风力机型是应用最为广泛的垂直轴风力发电机组，具有很高的应用价值，能够对垂直轴风力机的叶素-动量算法（BE-M算法）进行验证.

3 结论

(1)本文结合叶素动量算法，研究了Jacobs等人建立的关于达里厄型垂直轴风力机的几种数据库，对这几种不同的垂直轴风力机模拟气动数据库进行了研究比对，为垂直轴风力机的实际应用，所建立的数据库应该是可靠的，符合实际情况，一般数据库应该包括在低雷诺数和攻角±180˚的翼型空气动力系数，有些数据库做了一些合理假设之后，可以将数值拓展到此范围，从而使数据库得到完善，能够应用于工程实际.

(2)通过建立在几种数据库上的模拟仿真和实验数据比对研究表明，叶素动量算法模拟结果可以和大多数的数据库很好的吻合，但是动态失速条件下例外，尤其是在低雷诺数时，Sheldahl数据库以及Paraschivoiu和Lazauskas源数据库影响计算结果导致误差很大，就是由于在失速条件下对升力系数过低的估算.