对抛物型偏微分方程一种新的数值解法的研究∗

吐克孜艾肯,阿布都热西提阿布都外力

(新疆大学数学与系统科学学院，新疆乌鲁木齐830046)

0 引言

科学计算在各门自然科学（物理学，气象学，地质学和生命科学等）技术科学与工程科学（核技术，石油勘探，航空和航天和大型土木工程等）中起着越来越大的作用，在很多重要领域中成为不可或缺的工具.而科学与工程计算中最重要的内容就是求解在科学研究和工程技术中出现的各种各样的偏微分方程或方程组.在抛物型方程数值解法中常见的有Crank-Nicolson格式，跳点格式，三层显式格式，三层隐式格式，Saul’ev算法，分组显示方法等，但其各有利弊，计算量大，精度低.抛物型方程数值方法中的早期经典隐格式当推Crank-Nicolson格式，但由于此格式精度不够理想，有边界附近发生振动等缺点.随着高阶精度格式的发展，人们以很少使用它.近年来，阿布都热西提·阿布都外力提出了热传导方程的局部Crank－Nicolson方法[1]和修正局部Crank－Nicolson方法[2]，黄鹏展将该方法推广到一维变系数扩散方程[3]及burgers方程，开依沙尔·热合曼[4]用此法研究了一维对流扩散方程及本人对非定常对流扩散方程的研究，均得到很好的结果.本文根据这一方法对抛物型方程提出新的数值解法，这种方法在稳定性方面具有一定的优势并且具有计算简单，误差小，编程方便等优点.通过这项工作，对其他一些抛物型方程的数值解法也是一个很好的参考.

1 差分格式的构造

考虑一维热传导方程第一初边值问题

其中g(x)为给定的已知函数，a为热扩散系数.对(1)的空间微分项用中心差商代替，就得到半离散差分方程式

其中V(t)=是u(xi,t)的近似解，并且A是如下所示(N−1)×(N−1)的三对角矩阵.

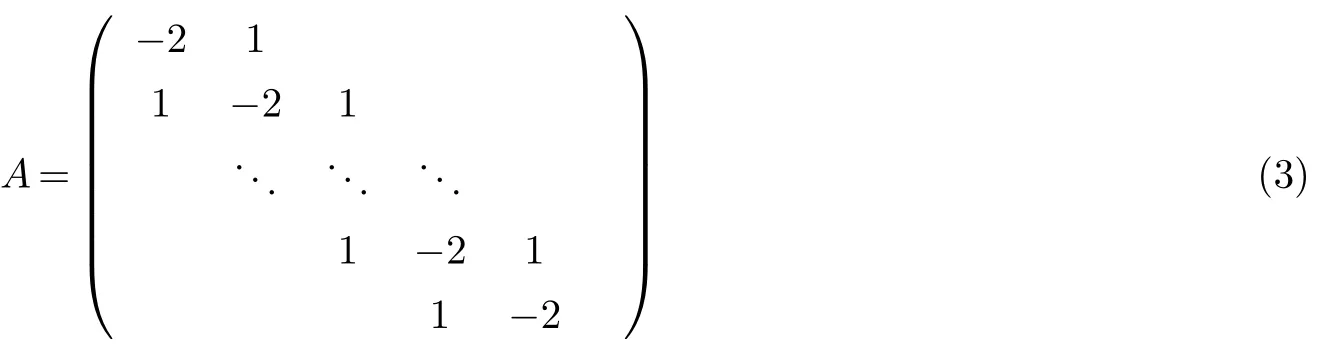
常微分方程（2）对于初值向量

的解可以表为

设τ=间步长,tn=nτ(n=1,2,···,N),进而有

对非线性项滞后一个时间步长，得到非线性项方程组（4）的线性化形式

其中矩阵A是（3）.考虑热传导方程的Crank−Nicolson格式，可以写成如下形式

(7)式可以改写成

(8)式的矩阵形式为

利用(6)和(9)式,有如下近似

命题1设矩阵A可以表示成

的形式，则

对于任何h,t成立，此处s是正整数与N有关.由(11)式，对任意σ=1，有

系数矩阵A按以下形式分成分块矩阵

这种按一个元素分裂得到的分块矩阵的特征值是-2，0或全为0.对任意的i=1,2,N−1,j=1,2,N−1，从（10）得

结合(12),(13),(14)，有

因此，结合（6）和（15），就得到一个新的差分格式

记Bij=A((N−1)−i)((N−1)−j))，为了改善精度，将Bij代入（16）就得到

其中Ii是一个i×i阶的单位矩阵，

类似于（21），有

从而，就得到了V(tn+1)的显示表达式.显然，(18)为显格式.由于把A分离成（13）这样的一些简单矩阵，虽然(13)中出现求逆过程，但是可以用手算直接正确地求出它的表达式，没有误差.这样就不需要直接解以大型矩阵为系数矩阵的线性方程组，所以此格式有计算量少，精度高的优点.这是数值计算上很重要的问题.

2 稳定性，相容性及收敛性引理

定理1设矩阵A能表示成的形式，即（13）表示的分裂形式，则差分格式(18)是无条件稳定的.

证明矩阵Aij的特征值是-2，0或全为0，因此的欧氏模不超过1.由稳定性充分必要条件知差分格式(18)是无条件稳定的.

定理2设矩阵A能表示成的形式，那么差分格式(18)的截断误差为O(h2+τ2).

证明由Taylor展开，易得差分格式（7）的截断误差为O(h2+τ2).而差分格式(18)的截断误差是N−1个（7）情形相乘得到的，故它的截断误差为O(h2+τ2).

定理3设矩阵A能表示成的形式，即（13）表示的分裂形式，任意常数，则差分格式(18)是相容的[2].

定理4设矩阵A能表示成的形式，即（13）表示的分裂形式，任意常数，则差分格式(18)是收敛的[2].

3 数值例子

考虑一维热传导方程的第一初边值问题

用变量分离法可得（20）式的解析解为

取a为网格比.下面取不同的网格比,用Crank−Nicolson法，修正局部C−N法，新提出的方法来求数值解，结果如表1，表2所示：

表1 h=0.1,λ=0.01时，解析解与近似解的对照

表2 h=0.1,λ=0.001时，解析解与近似解的对照

由表1，表2可以看出采用新提出的方法求出的数值结果与解析解的误差比采用Crank-Nicolson法的误差小，与修正局部Crank-Nicolson法的误差很近似.由表1，表2还可以看出随着网格比的减小，数值解越逼近解析解.

4 结论

本文在Crank-Nicolson算法的基础上,将所研究的偏微分方程转化为常微分方程组，利用指数函数的Trotter积分公式近似该常微分方程组的系数矩阵分离成分块小矩阵，再利用Crank-Nicolson算法求得结果，从而推出了抛物型方程的一种新的差分格式.进行了相应的理论分析和数值试验.该方法具有计算量少，无条件稳定的优点，通过数值试验验证了采用本文提出的一个元素的分裂算法的可行性，由此对复杂的数学物理方程出现的一阶，二阶甚至更高阶的微分项无法用中心差商代替，如果用其他差商代替,那么已有的分裂形式就不再适合，本文采用的分裂方式就给对复杂的数学物理方程采用修正局部Crank-Nicolson法提供了可能.