PMSM控制器逆变电路效率仿真分析

李良璋，王心坚

(同济大学，上海 201804)

0 引 言

目前，续航里程短是制约电动车发展的一个重要因素。为了提高电动车的续航里程，除了提高电动车车载电池的能量密度外，对电动车系统能耗的优化也是很重要的一个部分，因此，有关降低系统能耗的研究就一直没有停止过。电机控制器逆变电路在电驱动系统中承担着给电机直接提供三相交流电的任务，其损耗研究便是电驱动效率研究中的一个重点。由于在三相逆变电路中的电压、电流处于高频变化之中，因此，在实验中对这些量进行测量和记录就变得十分困难。以往的研究侧重于理论的公式推导。而纯理论推导出的结果由于考虑的因素不够全面，导致与实际实验结果往往相差较大;这就给仿真研究留下了一定的发挥空间。

本文建立起了较为精确的电驱动仿真模型，通过仿真实验，得到了在不同工况下的逆变电路各个元件的功率损耗;对IGBT的损耗作了进一步的细致分析;得到了逆变电路效率，总结其效率分布规律并与实际实验结果作比较，以验证仿真分析结果的正确性。

1 模型结构

根据文献［1］和电驱动模型以及矢量控制原理，本文建立起了电驱动仿真模型结构。

图1 电驱动模型

根据三相交流电机的矢量变换原理，id，iq电流分量的大小决定了三相交流电机的输出扭矩大小。该电驱动模型基于矢量控制原理，对id，iq电流进行控制，以达到对电机的输出扭矩的控制目标。

根据以上电驱动模型结构，我们在仿真软件中建立电驱动仿真模型，分为id，iq控制部分、PWM波生成部分、逆变器部分、电流反馈部分、电机模型及负载电机部分六个部分。

逆变电路模块是本文的研究重点，其损耗为本文的研究对象。该模块以PWM波生成模块所输出的PWM波和直流电源作为输入，以三相电流作为输出直接供给电机。因此，其工作电压电流较大，产生的损耗也就较大，成为了电机控制器损耗研究的研究重点。

搭建出该部分的仿真结构如图2所示。

图2 逆变器仿真模型图

模型中，IGBT参数根据某型逆变器模块说明中所提供的数据进行设置。

表1 IGBT的仿真参数

理论上，各相的输入的PWM波信号供给各相上桥臂IGBT，同时将对应的输入PWM波信号反向运算后供给下桥臂IGBT。因此，同一相的上、下两个桥臂的开关管控制PWM波信号应该是严格互补。

实际情形下，由于IGBT开关管的开启关断不可能在瞬间完成，而是需要一定的时间，因此会出现上下桥臂同时导通的情况，此时母线短路，其上的电流会很大，会发生电机控制器烧毁。在仿真过程中则体现为仿真结果出现过大尖峰，甚至仿真报错。在目前的逆变器控制中，为了防止这种情况的出现，一种常用的办法是引入“死区”，“死区”的引入方式有多种，本文采用的是使得上下桥臂的IGBT开启时刻均延后，在上下桥臂IGBT工作切换时，上下桥臂的IGBT先一同关断一段时间，如此便避开了同时导通的情况。这共同关断的时间便是“死区”。

输入的PWM波信号分为两路，一路经过一个非门，因此，得到了两路互补的PWM波信号。而后，两路均经过一个buffer缓存延时，使得上升沿均延后4 μs的时间(经过仿真实验确定，IGBT的开启和关断持续时间在4 μs左右，由于死区时间过长会造成系统反应变慢以及不足反应等不良影响，所以设为延后时间设为4 μs)。

经过死区生成部分后输出的PWM波形如图3所示。

图3 处理后的PWM波信号

输出的两路PWM波信号则分别供给上桥臂的IGBT和下桥臂的IGBT。

在整流电路中，当负载是开关功率变换器时，由于负载电流的突变，会产生极高的感应电动势。从这一点看，直流电源不仅仅提供直流电流，而是需要提供带有丰富交流成分的脉冲电流。这时的直流电源不仅需要低的直流内阻，还需要在很宽的频带宽度均具有良好的低阻抗，而宽频段的低阻抗作为整流器的直流电源是不会提供的。要想获得良好的宽频段的低阻抗必须应用性能良好的电容器，利用电容器电压不能跃变和电容器容抗随频率的升高而降低的特性，用电容器降低直流母线的交流阻抗。

由于这些原因，本文在逆变电路中引入了母线旁路电容，通过监控电容的电流发现，电容的引入也造成了损耗，因此在接下来的分析中，将开关管损耗、二极管损耗同电容的损耗一并分析研究。

2 仿真结果及分析

2.1 一个开关周期内的IGBT损耗研究

由于电机工作过程中，IGBT处于循环的开关状态，为了更好地研究IGBT的损耗规律，本文先截取了一个IGBT开关周期的相关电压，电流随时间的变化数据进行研究。

图4列出了在IGBT一个开关周期过程中，通过IGBT的电流、其两端的电压以及其损耗功率的波形图。

图4 一个开关周期内IGBT的电流、其两端的电压以及其损耗功率波形图

由图4可知，在IGBT的工作中期，开关损耗功率占据了总损耗功率的比重较大。这是由于在开启和关断的过程中，电压和电流不能突变，导致出现高电压和高电流同时存在的情况。由参考文献［2］可知，1 s内开关过程中的损耗:

式中:fs代表IGBT的开关频率。我们现在研究的是一个开关周期内的IGBT开关损耗，取fs=1，可得一个开关周期内的损耗:

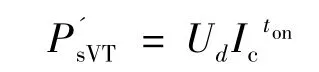
因此可知，损耗功率同电压和电流正相关并且和开启持续时间呈现幂指数关系，这同以上图中所示的仿真结果是基本吻合的。

2.2 一个开关周期中的二极管损耗分析

在逆变电路中，IGBT一般会并联一个旁路二极管，这个二极管起电流续流的作用。在IGBT关闭时，由于感性负载的缘故，在对应的相上的电流并不会立刻降为零，因此，电流便通过同一相的另一桥臂的旁路二极管续流。

图5 同一相位的上桥臂IGBT和下桥臂二极管的电流波形图

图5显示了位于同一相位的上桥臂IGBT和下桥臂二极管的电流波形图。从图中可以看出二极管电流和IGBT电流呈现互补的关系，将它们叠加到一起便得到了一个完整的正弦变化电流曲线。所以二极管在IGBT关闭时起到续流的作用，单位电周期内，IGBT的导通时间越短，则同相另一桥臂上的二极管的导通时间越长;IGBT的导通时电流越大，则当其关闭时，对应二极管导通电流也就越大。因此，二极管损耗同IGBT的损耗有较大的关系。

2.3 不同工作点下的逆变电路损耗分布分析

本文按照转矩不变、转速递增原则和转速不变、转矩递增原则分别选取了两组工作点并经过有限元仿真得到相关参数，如表2和表3所示。

可以发现，由于电机转矩恒定，其d，q相电流也是恒定不变的，其转速是由负载调速电机来调节。

表2 恒转矩工作点

表3 恒转速工作点

经过仿真分析，得到了逆变电路中各个主要能耗元件在各个工作点上的能量损耗。根据逆变器的输入电压及电流，经过MATLAB计算得到逆变器的各个工作点效率，如图6所示。

图6 逆变电路效率分布图

在恒转矩情形下研究IGBT的损耗变化，由于永磁同步电动机的输出扭矩大小同定子磁链矢量的幅值和相位角有关系，而定子磁链由定子电流励磁产生，所以在恒转矩工作时，转矩同电流有直接的关系，在本文中选取的几个恒转矩工作点中，定子电流(id，iq)均相同，由于损耗为电压和电流的乘积，因此，相同的d，q相电流为接下来的研究工作提供了一定的便利。

参考图4可以发现，IGBT一个开启关断循环功率波形图中的两端由于IGBT开启关断造成的功率尖峰在数量级上远大于导通时的功率损耗，基于此，本文认为，一个电周期中IGBT的开关损耗和导通损耗的比值对IGBT的损耗表现是一个十分重要的参考值。所以，本文对之前的信号导入MATLAB后进行进一步的分析，分离出导通损耗。计算如表4、表5所示。

表4 恒转矩(70 N·m)导通损耗

表5 IGBT开关损耗占总损耗的百分比

从表4、表5中可以看出，在转速提高的过程中，导通损耗功率是在增加的。然而由图6可以发现，随着电机转速的提高，逆变电路的总体效率也随之提高，这说明整体IGBT的总损耗功率是在减小的。所以，其功率减小的原因在于开关损耗功率的降低，开关损耗功率占总损耗功率的比重在降低。

而在恒转速的情形下，经过计算，可以得到IGBT的损耗功率如表6所示。

表6 恒转速IGBT损耗

可以看出，随着扭矩的提高，IGBT的损耗功率也随之提高。然而由于系统的总功率在扭矩增加的过程中也随之提高，所以系统的效率并没有太大的变化。

3 其他影响逆变电路损耗规律的元件损耗规律研究

3.1 二极管损耗规律研究

经过仿真及MATLAB数据处理，我们得到恒转矩条件下的二极管损耗功率。由于各个二极管功耗相同，因此表7列出其中一个二极管的各工况功率损耗。

表7 恒转矩条件下二极管损耗功率

可见，此时二极管的损耗功率随着转速的提高也呈现出降低的趋势。

利用MATLAB程序分析，我们可以分别得到占空比分布于十个以10%为梯度的档位(0～10%，10% ～20%，20% ～30%，…，90% ～100%)内 PWM波周期数占整个周期数的百分比和平均电流值。将二者相乘得到各个档位内相应IGBT原件的电流期望如图8所示。可以发现，随着转速的升高，IGBT上的导通电流期望偏向高占空比区域;对应的，由于IGBT的工作电流和二极管的工作电流相同而PWM周期互补，因此，二极管的电流期望应当向低占空比方向偏移。由于扭矩是恒定的，电流正弦波是相同的。这意味着，随着转速的提高，二极管导通时的电流波形包络线是相同的，然而在电流较大时(幅值附近)，其导通时间减少;在电流较小时导通时间延长。因此，随着转速的提高，二极管的损耗功率呈现下降趋势。

图8 IGBT的电流分布期望图

如表8所示，在转速不变的情况下，由于相电流的增加，导致了二极管的续流电流增大，从而二极管的损耗增加。

表8 恒转速工况下二极管损耗功率

3.2 母线电容损耗分析

在本文的逆变电路仿真模型中，母线同4个电容并联，电容值为3300 μF，其模型等效图如图9所示。

图9 电容模型等效图

经过仿真，电容上发生了一定的损耗，经过MATLAB计算，我们得到单个电容的各个工作点损耗，如表9、表10所示。

表9 恒转矩工况下电容单管损耗功率

表10 恒转速工况下电容单管损耗功率

从表9、表10的数据中可以看出，电容的损耗同电机的转速并无明显的关系;而同电机的转矩，即同母线上的电流关系较大，随着电机扭矩的升高，母线电流增加而增加。

4 结 语

(1)尽管存在着导通损耗，IGBT的损耗主要集中在开关损耗。造成开关损耗的主要原因是电流、电压的变化延迟。

(2)电机控制器逆变电路的主要损耗为IGBT的能量损耗，其次为并联电容、旁路二极管以及电路的其余杂散损耗。

(3)为了降低IGBT开关管的能量损耗，应该对PWM波的生成方式和电机控制算法二者同时进行优化。在电机的运行过程中，也应让其尽量工作在高转速区域，以提高逆变器工作效率。

(4)目前，对电机控制器逆变电路实际运行时各元件的损耗功率进行精确量化分析还有一定的困难。为了更进一步的分析，需要结合实际电路，获得更多的电路实际参数来改进模型，这些工作将在后续开展。

［1］李崇坚.交流同步电机调速系统［M］.北京:科学出版社，2006.

［2］贺虎成，杜京义，刘卫国.无刷直流电机驱动用IGBT逆变器能耗分析［J］.电力电子技术，2009，43(4):34 －36.

［3］Infineon Technologies.FS800R07A2E3 IGBT 模块产品说明［Z］.Infineon Technologies，2011.

［4］朱思国，金永顺.基于IGBT门驱动减小PWM逆变器死区影响的策略［J］.电气应用，2007，26(1):73 －76.

［5］THAPER N，BALIGA B J.A new IGBT structure with a wider Safe Operating Area(SOA)［C］//Proceedings of the 6th International Symposium on Power Semiconductor Devies and ICs.IEEE，1994:177－182.

［6］SEO J H.A new simplified space－vector PWM method for threelevel inverters［J］.IEEE Transanctions on Power Electronics，2001，16(4):545 －550.

［7］潘星，刘会金.IGBT功率器件工作中存在的问题及解决方法［J］.电力自动化设备，2004，24(9):9 －14.

［8］杨志，刘建政，赵争鸣，等.用于三电平逆变器中的IGBT驱动保护电路设计［J］.电力自动化设备2004，24(4):42－44.

［9］李东仓，吕振肃，杨磊.串联谐振并联输出IGBT逆变器研究［J］.电力电子技术，2000，34(2):16 －18.

［10］BIMAL K B.现代电力电子学与交流传动［M］.王聪，赵金，译.北京:机械工业出版社，2005.

［11］BUJA G S，INDRI G B.Optimal pulsewidth modulation for feeding AC motors［J］.IEEE Trans.on IA，1977，IA －13(1):38 －44.

［12］ZACH F C.Efficiency optimal control for AC drives with PWM inverters［J］.IEEE.Trans.on IA，1985，IA －21(4):987 －1000.

［13］TRZYNADLOWSKI A M，BLAABJERG F，PEDERSEN J K，et al.Random pulse width modulation techniques for converter fed drive systems－areview［C］//IEEE Industry Applications Society Annual Meeting，1993:1136 －1143.

［14］AGELIDIS V G，VINCENTI D.Optimum non － deterministic pulse－width modulation for three－phase inverters［C］//IEEE IECON Conf.Rec.，1993:1234 －1239.

［15］Mitsubishi Electric.General consideration for IGBT and intelligent power modules［Z］.Mitsubishi Electric，2001.

［16］JIAN S，BEINEKE S，GROTSTOLLEN H.Optimal PWM based on real－ time solution of harmonic elimination equations［J］.IEEE Transactions on Power Electronics，1996，11(4):612 －621.

［17］何凯航.SVPWM控制算法研究与实现［J］.机电工程，2011，28(10):1231 －1233，1245.

［18］寇正华，刘文生.基于BP神经网络的SVPWM算法的研究与仿真［J］.化工自动化及仪表，2011，38(2):190 －193.

［19］蔡宝平，刘永红，张海峰，等.基于人工神经网络的SVPWM技术［J］.电力系统及其自动化学报，2010，22(1):43 －47.

［20］万健如，魏志强，李莲，等.针对SVPWM死区问题一种新的控制方法［J］.电工技术学报，2006，21(7):105 －108，120.