转台伺服系统负载转矩估计研究

郑 颖，马大为，姚建勇，胡 健，董振乐

(南京理工大学，南京 210094)

0 引 言

火箭炮发射时负载瞬态变化大，其转台受不平衡力矩及燃气流冲击干扰力矩作用，系统参数具有不确定性。当转台伺服系统负载转矩发生变化时，传统控制器抑制负载扰动能力较差。采用负载转矩扰动补偿控制方法能很好解决负载扰动问题，使转台伺服系统在负载变化条件下实现快速稳定响应与精确跟踪。因此在负载转矩直接测量成本较高情况下进行负载转矩估计研究很有必要性。

负载转矩估计可采用负载转矩观测器。负载转矩观测器估计方法研究较多的是全阶状态观测器、滑模观测器、卡尔曼滤波器［1－3］。刘颖［4］等提出了基于扰动观测器的复合控制，由扰动观测器观测出系统中由于模型参数变化，负载改变等产生的扰动，并将观测值作为前馈量补偿到输入端，然后设计反馈控制器。国外学者Ahmad Akrad［5］设计了基于观测的永磁同步电机容错控制器。Mihai Comanescu［6］通过观测器进行非线性控制，并通过Lyapunov稳定性理论验证观测器的稳定性和收敛速度。本文采用扩展卡尔曼滤波(EKF)估计电机状态变量，在此基础上通过全阶状态观测器对负载转矩进行估计，改进负载转矩的估计性能，使系统具有动态性能好、参数鲁棒性强的特点。

1 问题描述

转台伺服系统的执行机构为永磁同步电动机(PMSM)，位置伺服控制系统的方框图如图1所示。伺服系统通过位置控制器、速度控制器和电流闭环控制对电机轴角速度进行控制，永磁同步电动机经过减速器带动负载进行控制。通常转台系统建模都进行了简化，将负载折算到减速器前端即电机输出端。因此对负载变化的估计是比较重要的。并且由于转台伺服系统具有负载变化大、受外界强干扰和不平衡力矩影响的特点，因此对负载转矩进行估计并进行补偿是提高控制精度的有效方法。

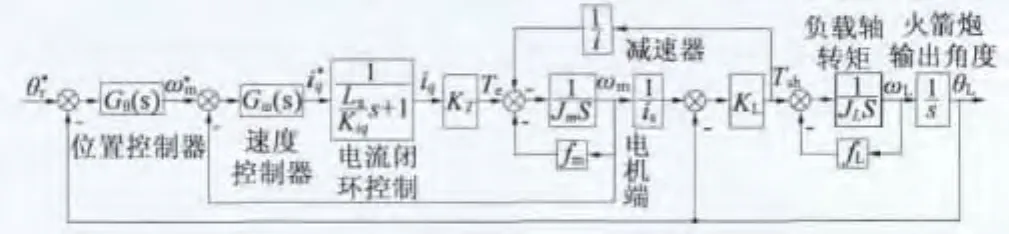
图1 火箭炮位置伺服系统方框图

2 伺服系统全阶状态观测器

以永磁同步电动机为执行机构的位置伺服系统运动方程:

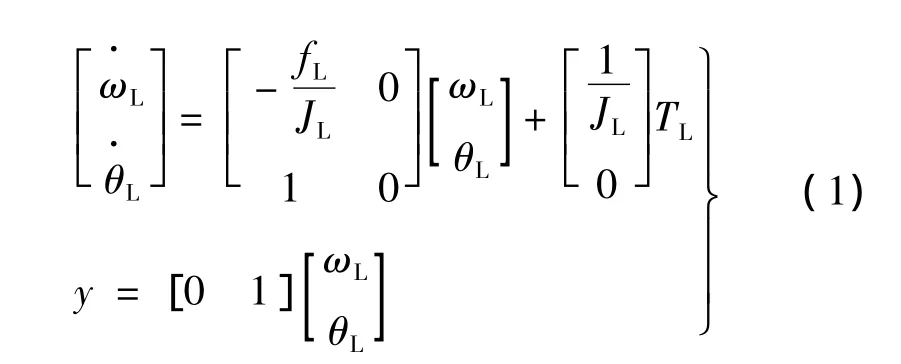
式中:ωL为负载角速度;θL为负载位置角;fL为黏性摩擦负载系数;JL为负载转动惯量;TL为负载转矩。

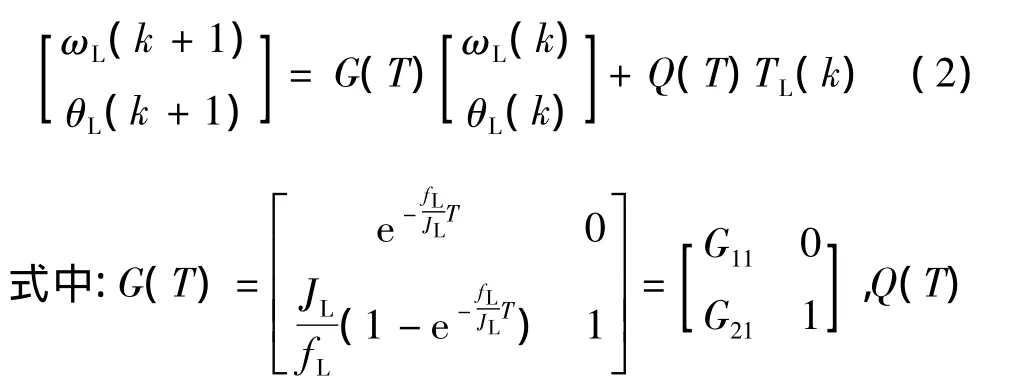
将负载转矩看作状态变量，令负载转矩TL(k+1)=TL(k)，则转台系统状态方程:

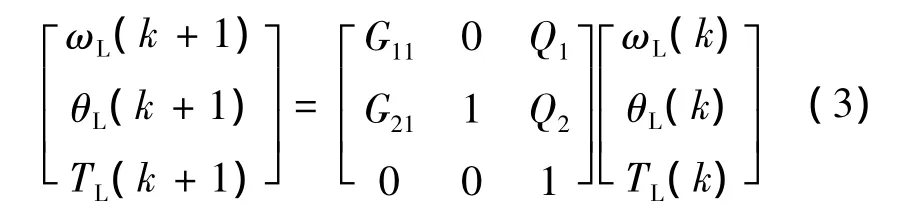
设计状态观测器:

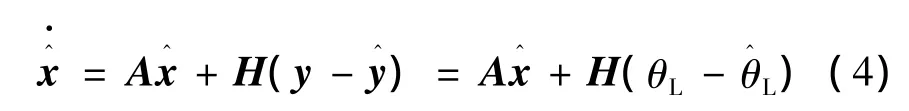
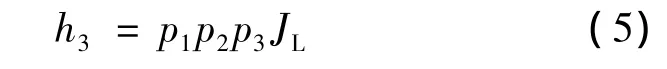
转台系统观测器方程:

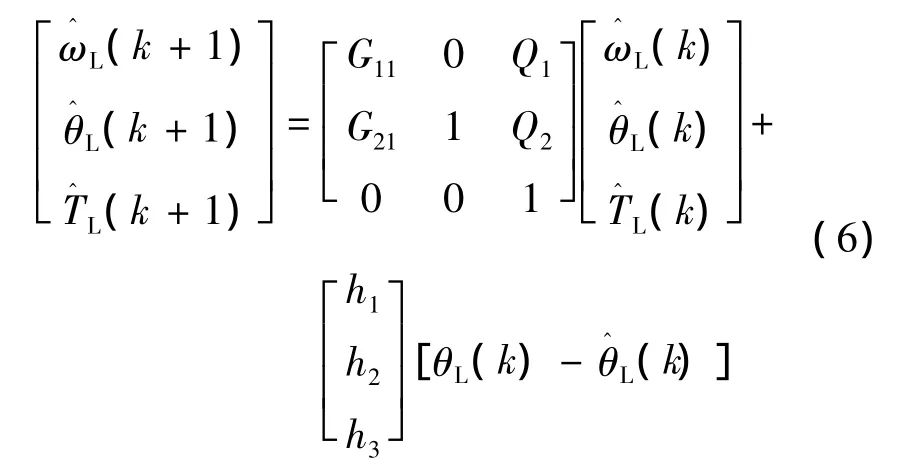
负载转矩观测器方程:

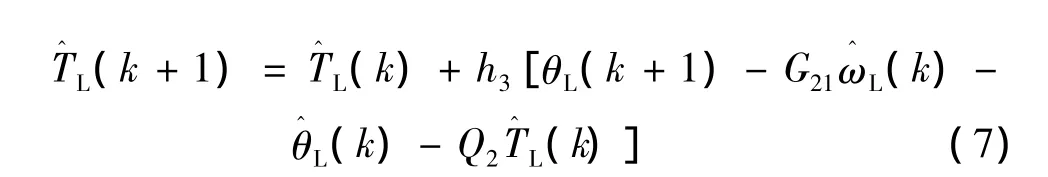
由式(7)可得由系统负载角度、角速度及已知参数G21和h3能估计系统负载转矩。下一步采用扩张卡尔曼滤波方法估计系统的角度和角速度。

3 负载转矩估计

3.1 基于扩展卡尔曼滤波的电机状态估计

扩展卡尔曼滤波器(EKF)是卡尔曼滤波器在非线性系统中的一种推广形式。永磁同步电动机系统作为非线性系统采用EKF进行状态估计能有效抑制系统误差和测量误差对状态估计的影响，快速准确地估计状态变量的值，收敛速度较快。

选取永磁同步电动机的状态变量和输入量分别为:x=［iαiβωθ］T，u=［uαuβ］T。式中，ω为电机转子电角速度;θ为电机转子位置。

永磁同步电动机非线性状态方程:

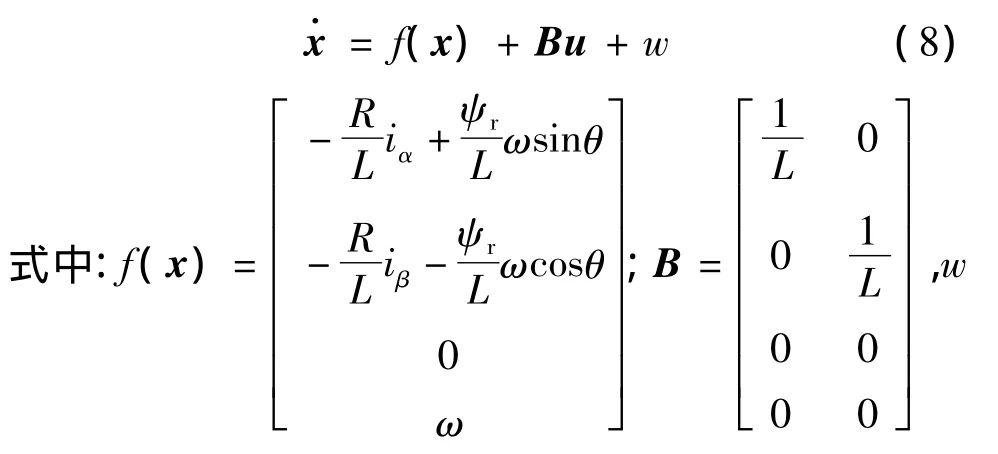
为系统噪声。

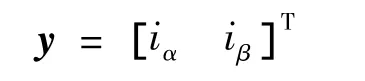
则系统量测方程:

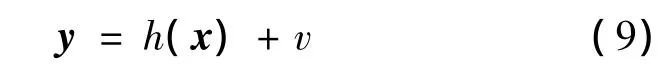
式中:v为量测噪声。对f(x)，h(x)进行线性化处理，f(x)，h(x)对应的雅克比矩阵:

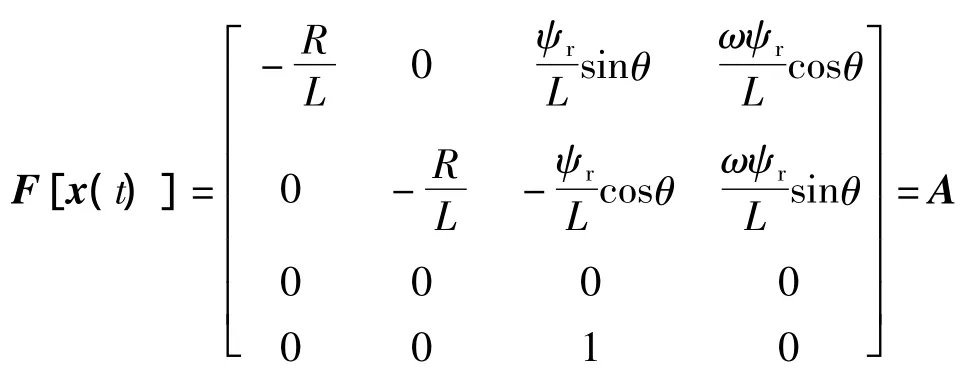
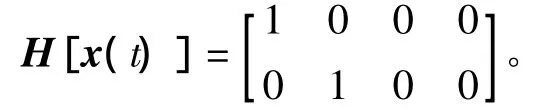
系统采样时间为T，则离散化后得:

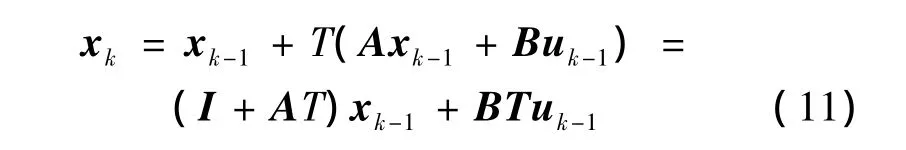
令Φ=I+AT，G=BT，则系统离散方程:

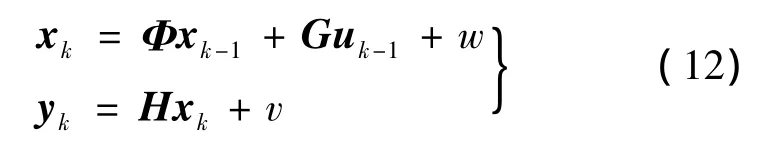
转台伺服系统永磁同步电动机离散型扩展卡尔曼滤波方程如下。

状态一步预测方程:

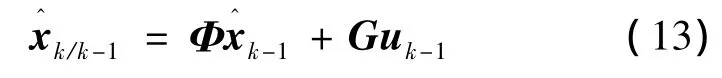
一步预测均方误差方程:

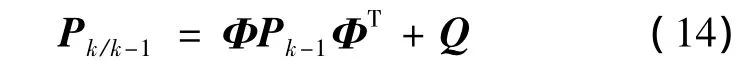
滤波增益:

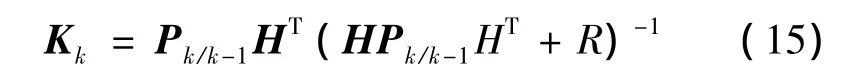
估计均方误差方程:

状态估计方程:

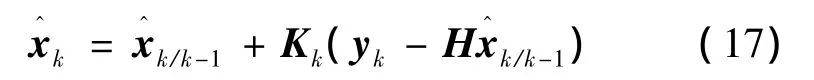
式中:Q为系统噪声协方差矩阵;R为测量噪声协方差矩阵。Q和R的选取对状态估计精度和数值收敛具有较大影响，通过仿真对两者进行取值。取Q

通过扩展卡尔曼滤波得到电机状态变量转速和转子位置角度，ωr为电机通过减速器后的负载轴前端角速度，则ωr=。式中:i为减速器减速比;p为电机转子极对数。将ωr近似为负载轴末端角速度即负载角速度。同理对于负载位置角的计算则由负载转矩观测器估计负载转矩的变化，并将估计值对参考转矩予以补偿，以解决负载扰动给系统带来的影响。

3.2 仿真结果

伺服系统电机参数:电感L=50×10－3H，电阻R=2.6 Ω，折算到减速器输入端的负载转动惯量J=2.627 ×10－3kg·m2，磁链 ψr=0.1 Wb，粘滞摩擦因数 B=0.001 N·m·s，i=240，p=4。输入电压uα=220sin ωt，uβ=220cos［sin(ωt)］，用 MATLAB的M文件编写程序，得到仿真结果如图2～图5所示。由图可知，通过扩展卡尔曼滤波方法可准确估计电机的电流值iα，iβ，电机转子电角速度和角度位置，从而可以准确估计电机通过减速器后端即负载端的角速度和角度。系统噪声和测量噪声协方差矩阵取值对估计精度有较大影响，在仿真过程中选取不同的数值进行比较。根据式(7)可由已估计的负载角度和角速度估计出负载转矩。负载转矩观测结果如图6所示。图6表明本文提出的负载转矩观测器可准确估计伺服系统负载转矩，当负载转矩瞬态变化时，该观测器能较好估计转矩变化，以对系统进行补偿，提高控制精度和抗干扰能力。

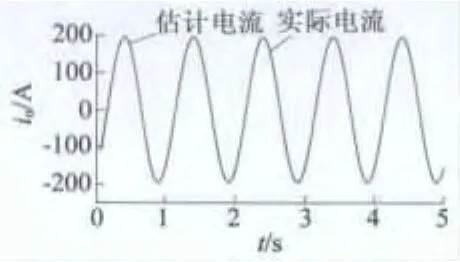
图2 iα的实际值与估计值

图3 iβ的实际值与估计值

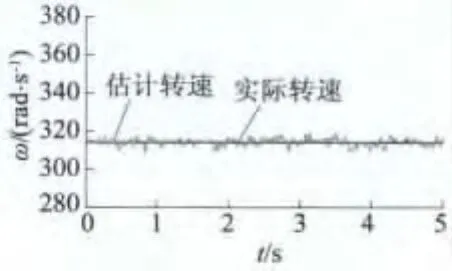
图4 电机实际转速与估计转速

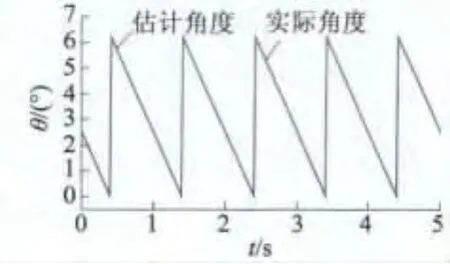
图5 电机实际转角与估计转角

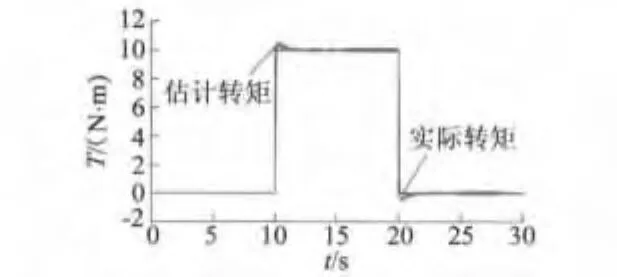
图6 伺服系统实际转矩与估计转矩

4 结 语

本文建立了基于扩展卡尔曼滤波的电机模型，并设计了负载转矩观测器。针对转台伺服系统瞬态负载变化大、系统参数变化大及受瞬态冲击强等干扰的特点，通过扩展卡尔曼滤波方法，估计了电机状态从而获得减速器输出端角速度和转角位置，并以此估计伺服系统负载转矩。扩展卡尔曼滤波准确估计了电机转子转速和位置角度，设计的负载转矩观测器对负载变化进行了准确估计以补偿给定参考转矩，为转台位置伺服系统的精确跟踪提供了理论依据。

［1］ZHENG Zedong，LI Yongdong，MAURICE F，et al.High performance PMSM control system based on extended Kalman filter［J］.Transactions of China Electrotechnical Society，2007，22(10):18 －23.

［2］刘子建，吴敏，王春生，等.基于自适应观测器和自抗扰控制的PMSM直接转矩控制［J］.系统仿真学报，2010，22(11):2702－2707.

［3］陈振，刘向东，靳永强，等.采用扩展卡尔曼滤波磁链观测器的永磁同步电机直接转矩控制［J］.中国电机工程学报，2008，28(33):75－81.

［4］刘颖，周波，方斯琛.基于新型扰动观测器的永磁同步电机滑模控制［J］.中国电机工程学报，2010，30(9):80 －85.

［5］AKRAD A，HILAIRET M，DIALLO D.Design of a fault－ tolerant controller based on observers for a PMSM drive［J］.IEEE Transactions on Industrial Electronics，2011，58(4):1416 －1427.

［6］COMANESU M，BATZEL T D.Reduced order observers for rotor position estimation of nonsalient PMSM［C］//2009 Electric Machines and Drives Conference.IEEE，2009:1346－1351.