城市道路间断流行程时间双峰分布
杨 帆,杨晓光,云美萍
(同济大学 道路与交通工程教育部重点实验室,上海 201804)
行程时间是表征路段服务水平的重要特征之一,城市道路间断流行程时间由于受到信号交叉口延误等因素的影响,呈现与连续流行程时间不同的特征.一般而言,连续流行程时间分布呈现单峰、右偏的分布特征,多以对数正态分布或Burr分布作为连续流的行程时间拟合分布[1-5].单峰分布模型已经被验证能够很好地描述高速公路及快速路的行程时间特征.在城市内部道路网中,定义上游交叉口出口道至下游交叉口出口道为典型路段,则路段的行程时间会受到道路线型设计,以及交叉口延误等待而呈现出间断流的特征,主要体现在:在相似的外界交通环境条件下,路段行程时间分布方差较大.从宏观统计学的角度而言,必然有一定概率的出行者由于延误而以较长时间通过路段,因此,间断流的行程时间通常呈现出双波峰特征.Taylor等[6]进一步对澳大利亚阿德莱德市两条城市主干道的行程时间数据进行分析,得出该行程时间表征出正偏、长尾的特征,并存在双波峰(bimodality)的特性,并在此基础上用Burr XII型分布来对路段形成时间和路径行程时间进行了拟合模型研究.同时,通过用两个单波峰(unimodal)分布的加权模型来推导出路段行程时间的双波峰分布,取得了不错的拟合效果.其研究成果表明,即使在连续流状态下,行程时间分布也是有一定概率呈现出双峰分布的特征.Jintanakul等[7]利用贝叶斯混合模型对高速公路行程时间分布进行了研究.其假设行程时间由两个正态分布的混合分布组成,用“快速部分”和“慢速部分”来归类快速行程时间样本及慢速行程时间样本.Ji等[8]利用美国CABS(the campus area bus service) 的 公 交 AVL(automatic vehicle location)数据,在Jintanakul等人的研究基础上,利用分层贝叶斯混合模型对城市路段行程时间进行估计.结果表明,该模型可以较好地描述路段行程时间的双波峰特性.但总体而言,对于城市间断流行程时间特征分布的研究目前还较少.更重要的是,间断流的行程时间受到如路段交通状况、下游交叉口延误以及高峰平峰等因素的影响,并非一个固定的双波峰联合分布的情况.因此,本文将以南京市RFID(radio frequency identification)数据为基础,分析城市间断流路段行程时间宏观分布特征,针对具体的交通流特征选择合理的联合分布模型.本文仍以较为公认的正态分布和对数正态分布对行程时间分布进行拟合,用最小二乘法拟合分布参数,最后对路段行程时间特性进行定性定量分析.
本文采用最小二乘法对城市间断流行程时间分布进行拟合,建立凸规划问题,利用Frank-Wolfe算法得到路段双峰行程时间分布函数及各参数.在此基础上,通过对这些参数的分析研究对路段交通状态进行评估.
1 间断流行程时间概率分布参数拟合
1.1 数据来源
RFID数据是以无线射频技术为基础,以射频标签与路侧接收器的通讯来获取车辆的信息数据.目前在南京主城区已经有超过55个主干道路段布设有RFID检测器,全市有超过70万辆汽车安装有RFID标签(南京市汽车保有量为117万辆),对于每个路段的车辆采样率均在80%以上.图1为RFID设备布设的示意图及RFID行程时间样本分布图.RFID设备可以采集通过该断面的所有装有RFID标签的车辆的信息,包括加密后的车牌信息、通过该断面的时间、车辆信息等.对于本研究而言,车辆连续通过上下游两个断面的时间是主要参数,通过该数据可以推出该车辆通过该路段所花费的行程时间.行程时间样本分布也明显体现出双波峰特性,并且呈现出不同的双峰分布形状.本文对不同的分布进行参数拟合,以更好地表述每一个路段的行程时间分布函数.

图1 南京RFID数据行程时间概念图及概率分布图Fig.1 Figures of interrupted travel time and possibility distributions based on RFID data in Nanjing
根据行程时间分布的不同形状特征,以及双峰模型的概念,城市间断流行程时间的概率分布通式如式(1)所示.

式中:f1(x)为第一概率密度函数(简称第一子分布);f2(x)为第二概率密度函数(简称第二子分布);f(x)为双峰分布的概率分布函数;F1(x)为第一累积分布函数;F2(x)为第二累积分布函数;F(x)混合分布的累积分布函数;λ为权重系数.
本文将具体地通过6种情形的分析,对行程时间分布参数进行拟合.6种情形分别为:正态分布(用N表示)、对数正态分布(用LogN表示)、对数正态分布+对数正态分布(用LogN_LogN表示)、对数正态分布+正态分布(用LogN_N表示)、正态分布+对数正态分布(用N_LogN表示)和正态分布+正态分布(用N_N表示).参数拟合的目标是为了让拟合后的函数与实测的样本之间误差最小,因此以最小二乘法的概念建立各拟合模型.
1.2 单一正态分布和对数正态分布拟合模型
用正态分布或对数正态分布对行程时间分布进行拟合较为简单.其模型如式(2)和式(3)所示.
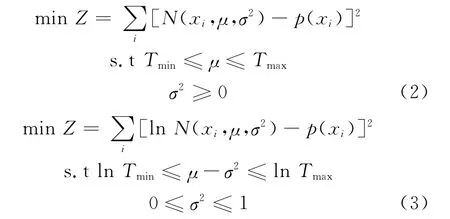
式中:Tmax和Tmin分别表示行程时间样本中的最大值和最小值;μ和σ2为概率分布的两个参数,根据特定分布具有特定的含义;xi为行程时间样本;p(xi)为xi所在的行程时间区间值在全样本中所占的比例.
单一正态分布和对数正态分布模型是在式(1)中令λ=0(或λ=1)而得的特殊情况.区别在于,在对数正态分布模型中,为了满足概率密度函数为右偏曲线,σ2为0到1之间的数.另外,对数正态分布中的均值μ为行程时间样本统一取对数以后得到的正态分布样本的均值,因此在约束集中需要在上下界处分别取自然对数值作为其约束范围.
1.3 LogN_N拟合模型
LogN_N分布的拟合模型如式(4)所示.
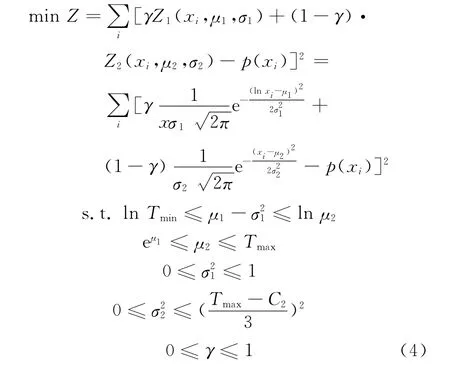
式中:γ为权重系数;C2为双峰模型的第二个波峰值.约束4是由正态分布的特性所得,如图2所示.如样本服从正态分布,则约68.3%数值分布在距离平均值有1个标准差之内的范围,约95.4%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围.称为“68-95-99.7法则”或“经验法则”.因此,以此约束来界定方差的范围.

图2 正态分布特性及其在行程时间分布中的应用Fig.2 Normal distribution features and its application to travel time distribution
1.4 LogN_LogN,N_LogN以及N_N模型
类似地,其他3类联合分布模型,LogN_LogN,N_LogN以及N_N模型也可以以此方式建模,如式(5)~(7)所示.如图3所示,C1为双峰分布的第一个波峰,C2为双峰分布的第二个波峰,p1,p2分别是双峰分布两个模数处对应的概率密度函数的概率值,M1,M2分别两个模数处对应的累积分布函数的概率值.可以看出,此6种情形的模型均为凸规划问题.目标函数为一个凸函数,而约束集为线性约束集(需适当将变量进行调整,如在式(6)中,需令y1=lnμ1,则可以将约束转化为线性约束).因此,可以用凸规划求解算法对其进行求解.



图3 双峰分布模型及其参数Fig.3 Bimodal distribution and its parameters
2 模型求解
Frank-Wolfe算法是经典的凸规划问题求解算法,其基本思路是从一个初始解出发,寻找目标函数最优下降方向,并沿此最优方向寻找最优步长,进行最优解的优化,直到目标函数达到最优.Frank-Wolfe算法多用于交通规划中的用户均衡分配问题,而本问题为普适性的凸规划问题,因此求解过程与交通规划中的Frank-Wolfe算法略有不同.以LogN_N模型为例,介绍具体的Frank-Wolfe算法的求解过程,其他模型求解与其基本相同.
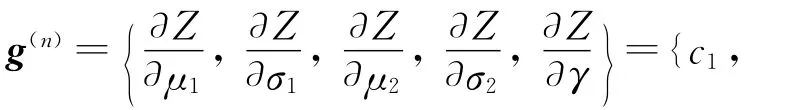
步骤3(寻找最优步长):建立线性模型如式(10)所示,用单纯性法求该模型的最优解为y(n).该步骤与传统交通规划中的步骤不同.在传统交通规划中,在初始流量加载的基础上,寻求到的最短路径即为该线性模型的最优解.但更广泛意义上来说,Frank-Wolfe算法需要对x(n)处进行广义线性规划问题求解,以得到最优解的优化方向.
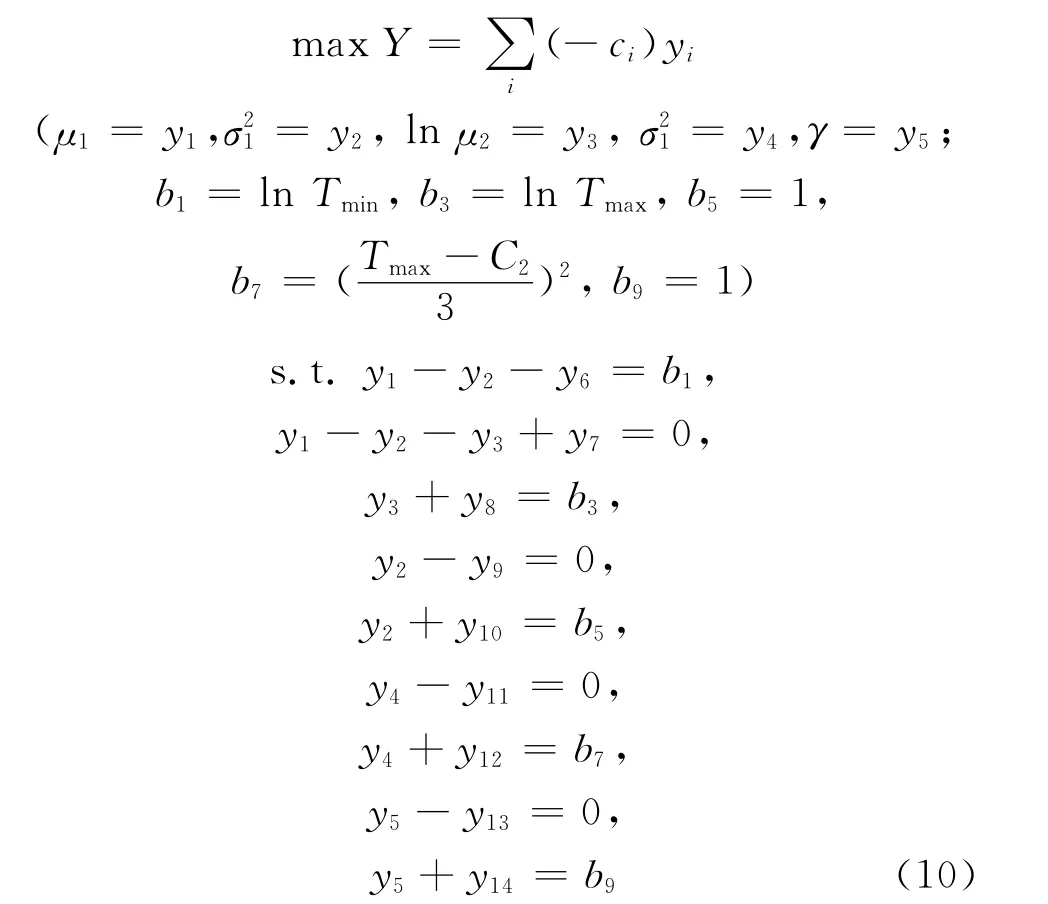
用黄金分割法求最优步长α.求最优步长α使得目标函数Z(x(n)+αy(n))最大.
步骤4(迭代更新).如果|Z(x(n-1)+αy(n-1))-Z(x(n)+αy(n))|<ε(收敛阈值),则停止迭代,得到最优解及最优目标函数;否则更新最优解,令x(n)=x(n)+αy(n),返回步骤2,重新更新计算.
3 数值分析
选取南京市若干个主要路段进行数据拟合分析,结果见表1,表2.表1为路段基本信息,其中B_ID是路段上游RFID点位ID,E_ID为路段下游RFID点位ID.表2为最优拟合模型及参数,其中用SECTION_ID来表述某一具体的路段,如“62456243”代表“中山南路南向北(金沙井到府西街)”.图4是6种组合分布的具体拟合情况.
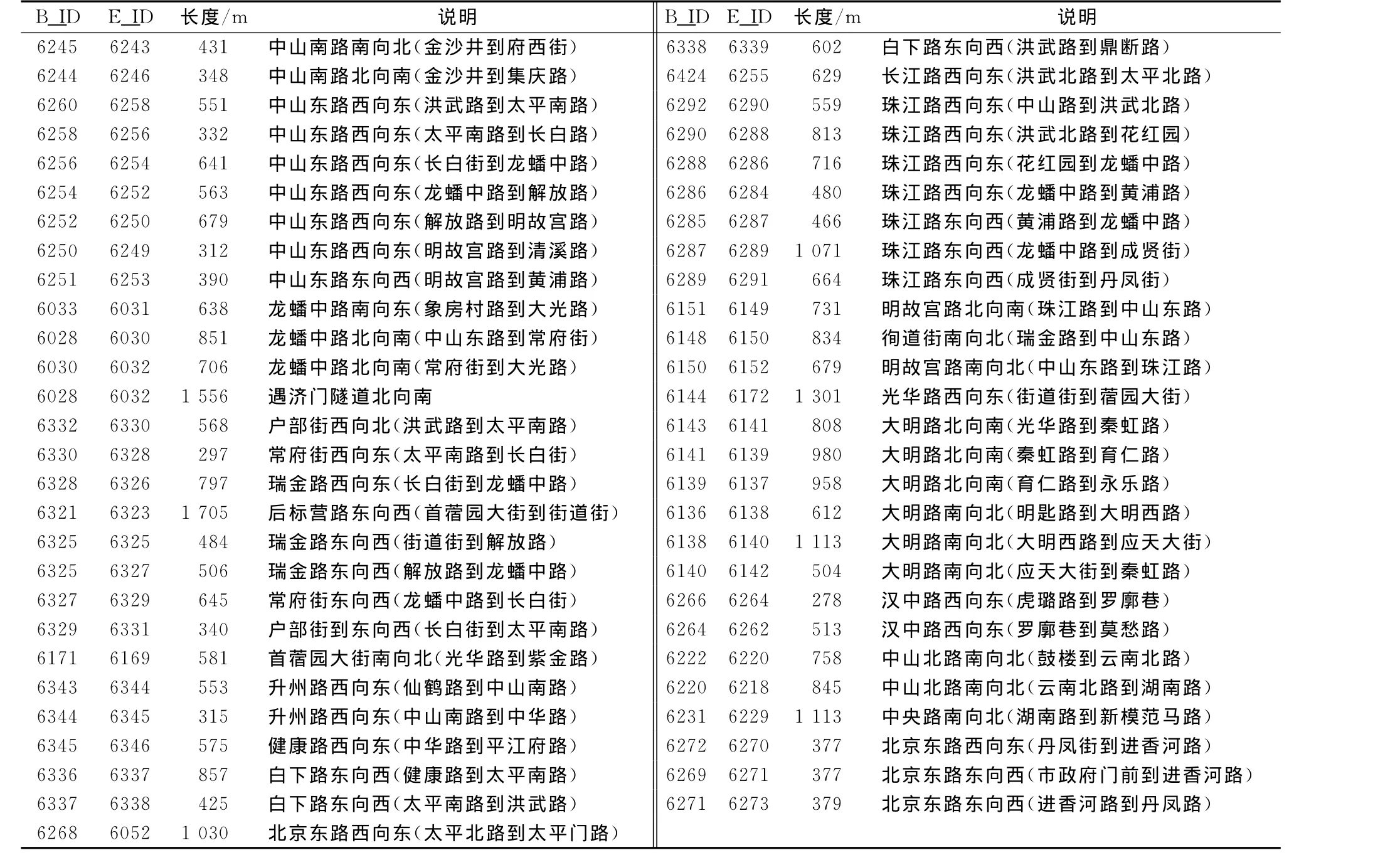
表1 路段基本信息Tab.1 Section_basic_information
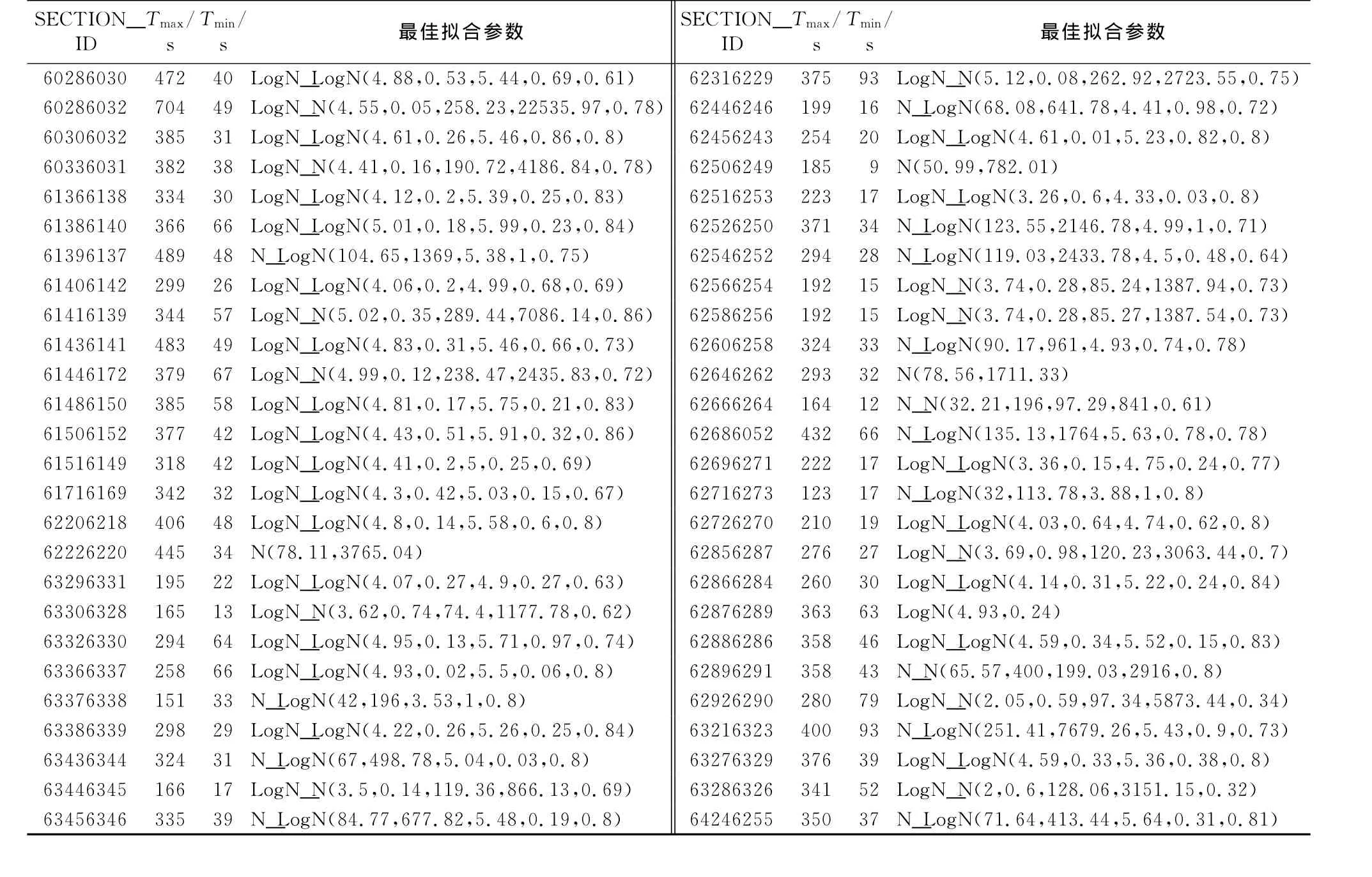
表2 各路段行程时间最优拟合模型及参数Tab.2 The optimized fitting model and its parameters of each section travel timefitting
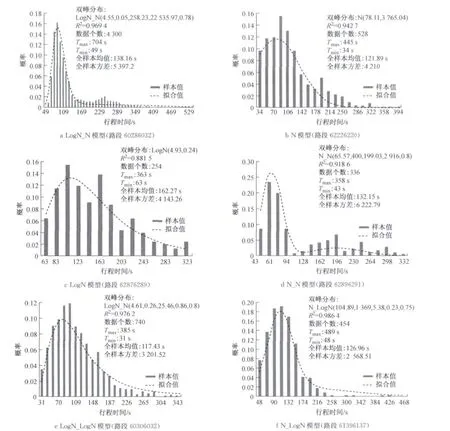
图4 6种不同类型的模型拟合曲线及样本分布图Fig.4 Fitting curves and sample distribution of six models
4 结语

图5 双正态分布及对应的双峰分布Fig.5 Two normal distributions and bimodal distributions
本文基于对数正态分布和正态分布,提出了6类不同的行程时间概率分布的单峰模型和双峰模型.以南京市RFID数据为基础,对实际行程时间分布进行了模型和参数的拟合,并分析了双峰模型对于城市行程时间描述的内涵.从广义的角度而言,本文提出的是一种理念和方法,并使用了正态分布和对数正态分布作为具体的分布函数进行拟合,目的是利用这两种合理并且拟合度较高的分布来印证本文对于间断流行程时间双峰分布的假设和研究,但并不表示所有的路段都可以用这两种分布来描述.因此,在后续研究中,可以利用其他分布,如Burr分布等,寻求其他的组合,以提高拟合的精度.
间断流双峰分布特性为间断流行程时间可靠性分析提供了新的思路.传统的可靠性指标,如BI(buffer index)等,均是基于连续流行程时间样本独立同分布的特性.在间断流条件下,则需要区分快速流和慢速流部分的行程时间样本,并重新定义符合间断流行程时间可靠性的一些指标,用以评估城市间断流路段通行质量.此外,本研究成果也验证了在城市道路路径选择、流量分配等环节中,不能简单地以传统最短路径算法来搜索路径,而应该基于城市间断流行程时间概率函数来寻找可行路径集,这将是本文的后续研究方向之一.
[1]Wardrop J G.Some theoretical aspects of road traffic research[J].Proceedings of the Institution of Civil Engineers,1952,1(2):325.
[2]Herman R,Lam T.Trip time characteristics of journeys to and from work[C]∥Proceedings of the 6th International Symposium on Transportation and Traffic Theory.Sydney:University of New South Wales,1974:57-86.
[3]Richardson A J,Taylor M A P.Travel time variability on commuter journeys [J].High Speed Ground Transportation Journal,1978,12(1):77.
[4]Polus A.A study of travel time and reliability on arterial routes[J].Transportation,1979,8(2):141.
[5]Al-Deek H,Emam E B.New methodology for estimating reliability in transportation networks with degraded link capacities[J].Journal of Intelligent Transportation Systems,2006,10(3):117.
[6]Taylor M A P,Somenahalli S.Travel time reliability and the bimodal travel time distribution for an arterial road[J].Road &Transport Research,2010,19(4):37.
[7]Jintanakul K,Chu L,Jayakrishnan R.Bayesian mixture model for estimating freeway travel time distributions from small probe samples from multiple days[J].Transportation Research Record,2009,2136:37.
[8]Ji Y,Zhang H M.Travel time distributions on urban streets:their estimation with a hierarchical Bayesian mixture model and application to traffic analysis using high-resolution bus probe data[C/CD]∥ 92th Transportation Research Board.Washington D C:TRB,2013.

