挑跌流消能防护形式中的水垫塘体型优化探索

严 涛，王兴建，刘廷海，刘 辉

(贵州省水利水电勘测设计研究院，贵阳550002)

1 问题的提出

在西部地区，水头落差大，水能资源丰富，中国建设了很多高坝来利用丰富的水能资源。代表性工程为金沙江下游梯级向家坝、溪洛渡、白鹤滩以及乌东德等特大型水利水电工程，这些重大水电工程大都修建在我国西部高山峡谷和地震高发区，地质条件十分复杂，施工环境差，重大事故危险隐患多，危险类型繁杂，危险控制难度大，并且存在泄洪流量大，水头高，泄流集中，存在很多高水头大流量泄流建筑物安全关键技术难题，坝下河床及岸坡的防冲问题十分突出［1］。

对于这些重大工程，高坝下游一般都采用护坡护底的防冲措施，水垫塘采用钢筋混凝土衬砌的硬化底板，根据其结构形式分为平底水垫塘和反拱水垫塘两种。很多学者从结构方面研究了水垫塘底板的稳定性。

平底板依靠底板自重和锚固钢筋来保持底板的稳定，结构设计时主要考虑正常泄洪期和检修期两种典型工况，均以浮升失稳控制［2］。一般为了抵抗巨大的动力压水，底板往往很厚，并要加抽排和锚固等相关措施。

根据练继建，杨敏，安刚等学者的研究，反拱型底板的稳定性大大优于平底板，在相同运行工况下反拱型底板安全系数＞平底板2 ～3 倍。

彭新民、许唯临、戴会超、Huai Wenxin 等学者从模型实验和数值模拟方面研究了水垫塘底板稳定性和水动力荷载特性。

但是目前对于水垫塘体型曲面和水动力荷载的关系研究是一个空白，反拱水垫塘的横剖面圆的半径如何确定，纵剖面底部曲线特征的描述，不同纵向坐标采用相同剖面是否合适都没有具体的研究。

冲刷实验所形成的稳定冲坑是挑射水流与抗冲材料平衡的结果，这个冲刷曲面和与之对应的水动力要素达到一种最优状态。

本文从水动力要素出发，进行水垫塘底板曲面的优化探索。

2 射流在水垫中的扩散规律

水垫塘内水垫应有一定的深度形成淹没冲击射流，避免出现自由冲击射流［3］。影响水垫塘安全运行流态的参数包括下游水垫深度H、射流水舌入水速度u0、入射水舌的厚度L、入射角θ 及单宽流量q 等参数，见图1。

由于挑流水舌经过挑坎的扩散参气作用，进入水垫塘后形成的水气两相流紊流状态非常复杂。为了在目标剖面上更直观地了解流速分布情况，将其简化为没有扩散参气的淹没射流。

如图1 所示，挑流水舌在水垫中的扩散区依次分为Ⅰ自由射流区、Ⅱ冲击射流区、Ⅲ壁面射流区，其消能过程分别对剪切消能区、撞击消能区和混掺消能区。这些区域都是相互影响的，如自由射流区变长，冲击射流区的水力要素也会随之改变进而对底板造成相应的影响。

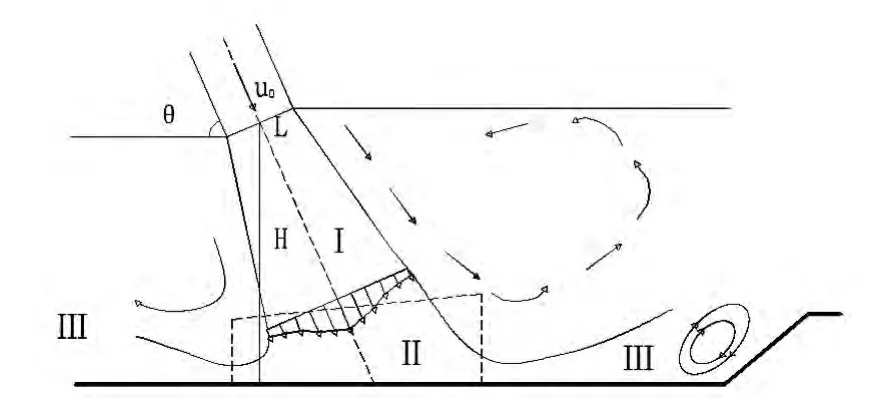
图1 水垫塘示意图

从能量的角度来说，有效地增加剪切消能区的范围，使这一区域消散的能量所占比例加大，那么撞击消能区需要消散的能量就会减少，对底板作用影响减弱［4］。

由于挑射水流在水垫塘中运动的三维状态较为复杂，现从横向剖面、纵向剖面两个方向探讨。

2.1 横向剖面

水垫塘中的水流往往处于高速紊流状态，而对于这种高速冲击射流的研究目前已经取得了丰硕的成果。

这些研究成果为优化水垫塘底板曲面形式提供了理论支持。在自由射流区和冲击射流区的流速分布情况李志伟由实验给出了一个无量纲流速分布公式:

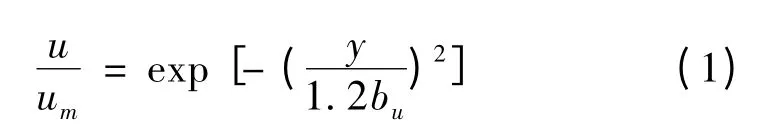
式中:u 为截面某一点上的流速;um为截面上的最大流速(通常为中线上的流速);bu为速度半宽，即bu=;流速半宽bu与射流流程的无量纲关系公式为:

截面无量纲流速分布公式为:

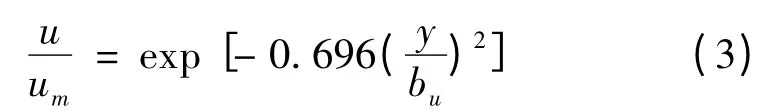
这和公式(1)非常接近，因此得到的流速分布情况具有较高的可信度。

射流不同截面流速分布见图2，x 为射流流程x =H/sinθ，y/L 为射流扩散的无量纲宽度。随着射流流程的增加，流速沿横断面逐渐扩展，并且轴线最大流速沿程减小，流速分布的钟形逐渐变得较为平缓。

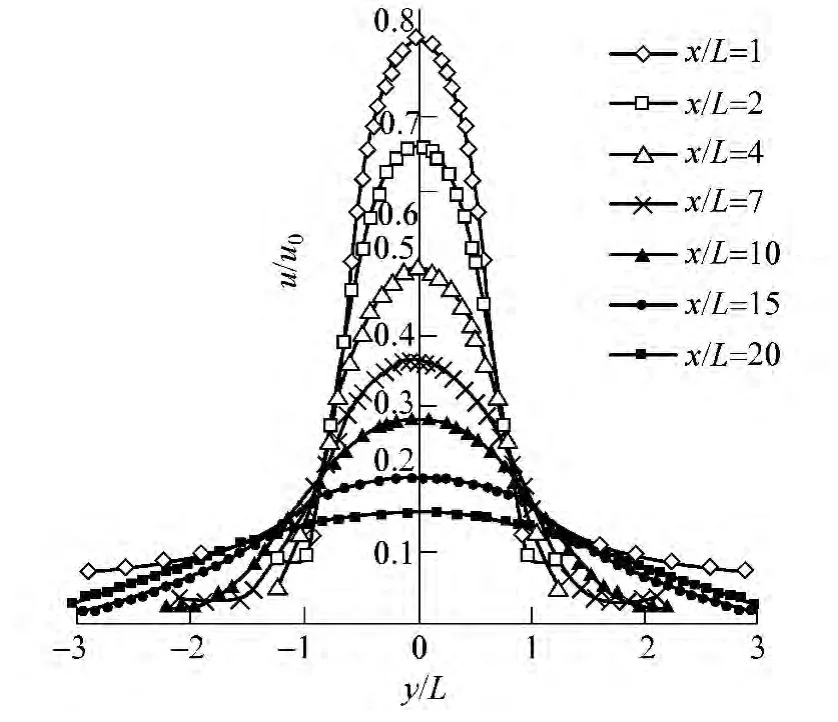
图2 射流不同截面流速分布

假设临近底板的流速全部转化为对底板的冲击压强，则底板上的压强分布类似于流速分布。对比平底水垫塘和反拱水垫塘，平底板上的冲击压强分布相对集中，同一底板上的不同部存在较大的压力差，并且紊流流速的瞬时变化使这种压力差处于一种脉动状态，这是目前公认的导致防护结构破坏的主要原因之一。而反拱水垫塘不仅在结构上比平底板稳定，而且反拱水垫塘横剖面的这种曲线变化改善了影响底板的水力要素。

水垫塘冲击区横向剖面见图3，轴线上的流速最大，到达底板的距离最远;远离轴线时流速减小，但是相应的离底板也较近，通过控制横剖面曲线的变化理论上就可以使底板所受冲击压强相等，避免出现平底板上的冲击压强集中的不利现象。

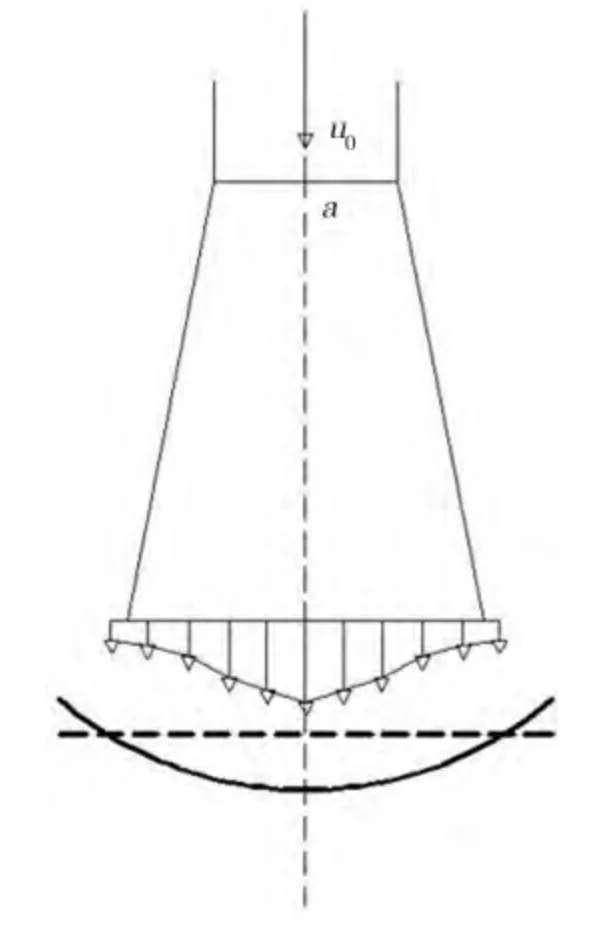
图3 水垫塘冲击区横向剖面

2.2 纵向剖面

在纵剖面上，水垫塘纵向剖面见图4，与横向剖面的扩散相似，由于压强与射流路径成反比，增加水垫塘深度能使射流扩散，流速分布更均匀，不存在明显的峰值。

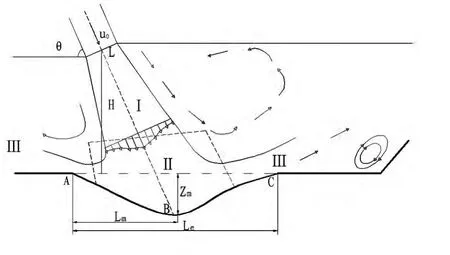
图4 水垫塘纵向剖面

并且根据研究，越靠近射流轴线时，均冲击压强随水垫深度的增加而减小得越快。因此，增加水垫深度是减小冲击压强峰值使其均匀分布的有效途径。

根据水垫塘长度的估算公式，水垫塘长度往往比较长，如果在整个长度方向上加深水垫塘的深度，增加的工程量是非常巨大的，而且在狭窄的河谷中开挖过深对两岸山体的稳定也非常不利。

由此，在冲击区局部加深水垫塘深度使底板形成有别于现反拱水垫塘底面的曲线，使之既能继承反拱水垫塘在结构上的优点又能从水力要素上改善底板的受力状态。但是注意到由于入射角一般不是90°，射流扩散并不是横向剖面上的轴对称扩散，因此底板纵向剖面上的曲线又有所不同。

稳定冲坑曲面是射流水体与抗冲体相互作用的一个结果，水力要素与防护结构处于一个最佳状态。类似于WES 曲线，将这一自然平衡的曲面应用到水垫塘底板的优化是顺应规律的。根据实验数据得到了几个描述曲面几何特征的公式，对于水垫塘底板的优化有借鉴意义。

最大深度公式为:

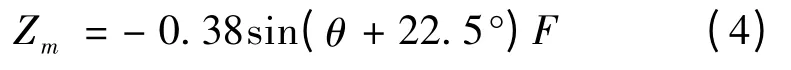
冲刷开始处到最深点的距离公式为:

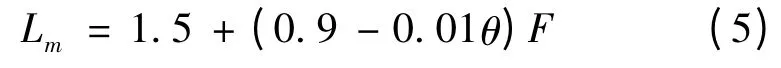
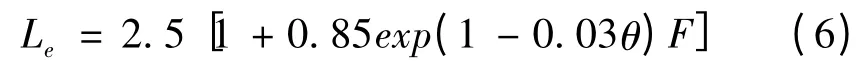
冲刷开始到冲刷结束的距离公式为:以上公式中入射角θ 的范围为30°≤θ ≤90° ，F为与来流条件、下游水垫深度及抗冲体的性质有关的参数。在水垫塘的设计建设中，根据实际情况选取不同下游水深，以上几个参数也会有相应的调整，使所确定的底板形态始终是处于水力最优状态。

一般最先破坏的地方并不是在冲击压强最大的冲击区，而是在冲击区与壁面射流区交替的区域(见图4)，此处为水流转向之后的收缩断面，根据伯努利方程，流速增加导致此处底板上部压强减小，而底板下部并没有同步这一变化，并且缝隙的存在使得底板上下面压力不一致，也就是通常说的上举力，对底板有巨大的破坏作用。另外，射流水体流线在碰到底板后弯转，向上挑起形成回流，靠近底板处的回流对底板作用就非常明显，改善这个区域的流态是防止底板发生破坏的关键。Le的长度及这段曲线如何与后面的底板平顺的过渡显是尤为重要。将底板纵剖面改进成以上描述的曲线能较好的顺应流线，达到预期的目的。

3 底板曲面的演进

水垫塘平底板块的稳定是以一个独立底板块的升浮作为控制条件。由于各底板块间约束作用较小，水舌作用范围内的所有底板块都要满足平衡方程方能使水垫塘底板保持稳定。在底板缝隙止水设施破坏，锚固力失效的条件下，足以使底板块拔出座穴。一旦水垫塘中有一底板块掀起，则会引起周围其他底板块的连锁破坏，导致水流冲刷河床基岩。反拱水垫塘利用拱形结构的力学特性，将射流冲击荷载传递到两岸山体或拱座，充分发挥混凝土的抗压特性和拱结构的超载能力，提高底板的整体稳定性。根据冲击区横剖面的水力要素分析，这种形式还能主动适应水流的流速分布进而改善水流给底板的作用力，使底板上的冲击压强分布均匀，相对于平底是一个巨大的进步。

目前的反拱水垫塘的横向剖面仍没有一个确定的控制方程来指导，修建时存在较大的随意性，而且在纵向剖面上仍是平底，不能很好的适应挑射水流在水垫塘中的流动扩散规律。根据以上纵向剖面的水力要素分析，纵向剖面也有做成类似反拱水垫塘横向剖面的必要，但是考虑到入射角的影响，冲击区下游比上游所受水流作用大，底板纵向剖面曲线有别于横向剖面的对称形式。图4 中曲线ABC 上段AB 就顺应来流，而下段BC 需要与下游自然的过渡，消除剧烈的旋滚脉动对底板的破坏。结合冲刷实验的研究成果，提出将水垫塘也做成类似冲刷平衡中的曲线的设计想法，将传统反拱水垫塘在纵向剖面将底剖改进为合适的曲线，在三维上形成双曲反拱，使水力要素与水垫塘防冲结构两者之间达到最佳的平衡状态。

4 结 语

本文从水力要素出发，根据射流在水垫中的扩散规律，流速随流程的衰减关系，比较分析了平底水垫塘、反拱水垫塘及在纵向剖面上改进的反拱水垫塘的受力情况，得出在纵向剖面上改进的反拱水垫塘为最优形式的结论。目前尚不能确定具体的底板横、纵剖面曲线及底板三维曲面控制方程，需要进一步通过物理模型实验及数值模拟来深入研究。

［1］戴会超，许唯临. 高水头大流量泄洪建筑物的泄洪安全研究［J］. 水力发电，2009，35(1):14 －17.

［2］杨敏，崔广涛. 水垫塘底板稳定性控制指标的探讨［J］.水利学报，2003(08):06 －10.

［3］练继建，杨敏，安刚，胡明是反拱型水垫塘底板结构的稳定性研究［J］. 水利水电技术，2001(12):24 －26;76.

［4］彭新民，王继敏，崔广涛. 拱坝水垫塘拱形底板受力与稳定性实验研究［J］. 水力发电学报，1999(02):55 －62.