斜压罗斯贝变形半径优化的误差相关尺度及其对最优插值效果的改进

王公杰，张韧＊，陈建，王辉赞，王璐华

（1.解放军理工大学 气象海洋学院，军事海洋环境军队重点实验室，江苏 南京211101）

1 引言

随着卫星遥感技术的兴起，各种卫星遥感资料包括海表面高度数据、海表面温度数据等为海洋研究提供了大量的海表面资料。近年来，越来越多的现场观测计划如Argo计划、TAO计划以及WOCE等也为海洋学研究提供了大量的三维观测资料。但无论是卫星遥感资料还是现场观测资料，在时空分布上都存在各自的缺陷。如何将二者有机结合，促进物理海洋动力学和热力学研究以及提高海洋可预报性，具有重要的科学意义和应用价值。

与数值天气预报一样，精确获取海洋动力模式的初值，对实现海洋可预报性起到至关重要的作用，而通过将观测资料与动力模式结合获取初值的过程便是资料同化［1］。由于海洋资料同化对于计算资源要求很高，最优插值等计算代价相对较低的同化方法仍然在资料同化中占有重要的位置。欧洲中尺度天气预报中心和加拿大一些业务部门都曾采用该技术作为业务化分析的主干。随着四维变分、集合卡曼滤波以及集合卡曼平滑等方法逐步应用到海洋资料同化并取得诸多进展，专门针对最优插值的研究已经不多见，学者们多是将最优插值作为变分同化以及卡曼滤波等方法的对照。尽管如此，业务化系统中应用最多的仍是三维变分［2］或最优插值方法［3—4］（Kalnay证明了对于单变量的分析时最优插值与三维变分在解决同一问题是具有等价性［5］）。

最优插值方法的表达式为：x a＝x b＋K（y o－Hx b）［6］，其中x a为最优插值得到的变量分析场；x b为背景场（一般从气候态数据得到）；y o为离散的观测量；H为观测算子；K为权重矩阵，也叫增益矩阵，是衡量观测值与背景值相对大小的权重因子。

经推导可得：K＝BHT（HBHT＋R）－1，其中B为背景场误差协方差矩阵（以下简称矩阵），R为观测误差协方差矩阵。对于海洋三维场，全球尺度的背景场误差协方差的计算量很大，在不考虑平衡算子的前提下，通常的做法是进行矩阵分解，即B＝D1／2CD1／2，其中D是对角方差阵，对角线上的元素表示格点的方差，一般利用气候序列方法求得，C是相关矩阵，一般利用空间滤波算子计算得到。最简单最常用的方法将C矩阵中的每个元素μij（即i，j两空间点的相关系数）表示成水平距离的函数，常用的形式有高斯函数、二阶自相关函数等。高斯函数形式的相关系数表达式为：μij＝exp（－／2），其中r ij代表两点间的空间距离，Lφ代表误差相关尺度。误差相关尺度取决于变形半径，它通过改变背景场的误差协方差的结构来影响观测信息被订正到背景场上的程度，以及观测信息在计算空间格点的传播方式和滤波方式［7］，并影响最终的同化效果。

图1 最优插值方法的一种实现途径

目前关于海洋资料同化中矩阵的构建主要有3个步骤：一是利用传统的NMC方法、气候序列方法、观测余差法等计算误差标准差；二是采用不同复杂程度的空间滤波算子构建误差相关矩阵，如水平距离相关函数法、扩散方程解算子法［8］等；三是研究变量间相关对背景场协方差的影响，即对矩阵施加物理约束。相对于大气而言，海洋中各物理量在时间尺度上变化相对较慢，且观测稀缺，因此计算误差标准差的方法绝大多数限于气候序列法。当进行单一变量同化时，研究的重点归结于选出更加合理有效的空间滤波算子。相对于扩散方程解算子法，水平距离相关函数法更容易实现，因而在资料同化中的应用也更广泛。舒业强［9］、Jacob等［10］以及 Meyers等［11］的工作表明采用水平距离函数作为空间滤波算子是合适的。

然而，前人的研究存在两个方面的问题：一是采用全场均一的误差相关尺度或者把整个分析海域分割成若干子区域，每个子区域设置为均一尺度，这种做法显然无法考虑海洋中不同物理过程对B矩阵结构的影响；二是Meyers等的工作对观测资料的要求较高，无法进行连续的、大面积的插值实验。尽管Kalnay［5］以及 Reynolds等［12］的研究中均表明，误差相关尺度取决于斜压罗斯贝变形半径（以下简称变形半径），但是探究其对最优插值效果改进的研究尚未开展。随着基于客观分析的高分辨率气候态温盐数据的出现，精细刻画近海陆架陆坡等浅海海域的变形半径变成可能。本文利用最新的高分辨率区域气候态数据计算变形半径，探讨基于变形半径优化的误差相关尺度方案对最优插值结果的改进。

2 计算方法和实验数据

2.1 变形半径计算

变形半径是研究大尺度海洋环流和刻画中尺度海洋现象，如中尺度涡、沿岸射流和赤道流等的重要尺度。同时，变形半径也是数值模式参数设置的重要参考量，如Qiu［13］指出变形半径决定了1.5层模式厚度设置，而 LeBlond和 Mysak［14］和 Pedlosky［15］分别证明了数值模式网格尺度大小要与变形半径相匹配。可见精确刻画浅海海域的变形半径对于海洋动力学和资料同化的研究均具有重要意义。

在理想状况下，变形半径可以从准地转位涡方程中得到［16］。假设垂向速度可表示为互不相关的垂向函数和水平函数的乘积，即：w（x，y，z，t） ＝φ（z）W（x，y，t），那么采用模态分离技术，可将原始方程转化为：

式为：N2（z）是声速，ρ是海水密度。本文采用中性密度梯度算法计算N随深度的分布。方程（2）的边界条件是：z＝0时φ＝0；z＝－H时，φ＝0，其中H代表水深。

采用中央差格式离散特征值方程，求解斜压罗斯贝变形半径的问题变成了求解方程（2）的Sturm－Liouville特征值问题［17］。为保证解出的特征值为实数，必须保证特征矩阵的对称性，故先对温盐剖面数据进行Akima插值，得到等间隔深度处的温度和盐度值。其特征值μ＝－（Chelton等［18］），而第m阶变形半径λm的表达式如公式（3）、（4），式中的c m是第m模态的斜压重力波速。

图2 东亚海域水深分布（a）和第一斜压Rossby变形半径分布（b）

2.2 实验区域和数据

研究区域选取中国东部海域及其附近海域（以下称实验海域）。该海域受季风影响显著，外有强西边界流（黑潮）和太平洋潮波传入作用，内有长江、黄河等大陆径流输入淡水泥沙等引起的浮力驱动，明显的季节变化形成独特的温盐结构和复杂的环流系统。黑潮作为该海域最重要和典型的海流，携带大量的热量流向中高纬度海域，其变化会对中国近海的温盐和环流结构产生重要的影响，同时也显著影响着周边大陆的气候。研究该海域斜压罗斯贝变形半径的变化，对进一步认识海洋动力过程，了解大尺度环流和中尺度涡旋，以及确切刻画海洋环境的气候态特征，大有裨益。

由WKB近似公式可以看出，斜压重力波速显著地受到地形变化和海洋层结的影响。在实验海域，海底地形复杂，如图2a所示：在西边界流海域，琉球海沟、东海大陆架以及一系列的海脊、海山纵横交错，地形的水平梯度很大，变形半径也随地形显著变化。另一方面，由于近海陆架、陆坡区域的海水性质受陆地、季风以及潮汐的浅海效应影响，海水的垂向混合机制复杂，层结变化差异明显，也将导致变形半径的强烈变化。这要求我们必须采用高分辨率温盐资料，来描述变形半径的精细变化。

美国国家海洋数据分发中心（NODC）与韩国国立渔业发展研究所合作开发了一套基于客观分析的高分辨率的区域气候态温盐数据：水平分辨率有1°、（1／4）°和（1／10）°3种；垂向按照 NODC标准层从0 m向下到5 500 m分为102层，覆盖范围是24.0°～52.0°N，115.0°～143.0°E。本文采用（1／10）°分辨率的温盐数据计算变形半径，分析变形半径的地理分布特征及其影响因子。

求解Sturm－Liouville特征方程，得到实验海域第一斜压Rossby变形半径的空间分布，如图2b所示。可以看出，变形半径在近岸海域相对较小，大部分区域都小于10 km，这可能是由于近岸海域混合较明显，浮性频率上下均一造成的，说明近海的水文特性主要受局地小尺度过程的影响；而在琉球群岛链附近，由于地形变化剧烈，变形半径分布与地形变化类似，岛链两侧深厚海沟的存在使得变形半径迅速从几公里变为40 km左右，变形半径的梯度出现极值，这说明该海域地形对变形半径的影响占据主导地位，这与日本本州岛东京湾正南偏东方向的七岛—硫磺岛海岭附近的情形相仿。西北太平洋海域主要受到副热带流系以及大洋西传的Rossby波的控制，变形半径（大约为50～60 km）的分布，主要体现了这些物理过程的尺度。黑潮流经海域，由于黑潮携带来自北赤道流的高温、高盐海水与东中国海局地水文性质存在较大差异，形成了明显的西边界流锋区，锋区变形半径的分布与东海黑潮的流线分布基本吻合，说明该海域海洋动力过程的水平特征尺度受黑潮影响很大。

2.3 对比实验设计

模式框架采用法国的ISAS（In－Situ Analysis System），它是一套基于最优插值的数据融合系统，已经实现业务化运行［3］。分析表明，无论采用高斯函数或二阶自回归函数（SOAR）作为拟合函数，当误差相关尺度发生改变时，相关函数曲线及相应的背景场误差协方差矩阵的形式会发生相应的调整，进而直接影响最优插值结果（图3）。从最优插值原理看，实测资料的数量和质量会影响影响插值结果，在确保质量的前提下，实测资料分布越广泛，所含有的局地、实时的海洋信息就越多，所得到的插值效果也越好。在实测资料数量有限的前提下，合理扩大误差相关尺度，可以防止插值结果所包含的观测信息过少，从而在一定意义上可以改进插值产品。然而，误差相关尺度并非越大越好，相关尺度越大，其平滑效果越明显，过大时可能会因为不同观测数据之间相互干扰或者抵消，使得插值效果变差。对比实验中，分别引入了均一化尺度和基于变形半径的尺度两种方案，而ISAS自带的尺度方案（双尺度方案：热带副热带海域呈现大尺度均一的特征，中高纬度随纬度升高而减小）作为实验对照方案。均一尺度方案分别选择20 km，50 km，80 km，100 km，150 km，200 km为相关尺度；而变形半径方案，则通过将误差相关尺度分别设置为不同的变形半径倍数（即空间点的误差相关尺度设为该点变形半径的倍数），来实验探究其对插值结果的影响。实测资料只选择Argo剖面，其他来源的实测资料如：CTD、XBT等用来对比评价插值产品的质量。评价插值效果，采用均方根误差RMS作为指标，RMS的计算方法如公式（5），其中指标m代表垂向的层次，n代表各个层上观测点的个数，N代表观测点的总数。其中，xanai，j是由分析场上的格点值插值到观测点的位置处得到。实施最优插值过程中，只对上层1 000 m海域的温度场进行插值实验，垂向分为102层，水平的网格为（1／2）°×（1／3）°的 Mercator格点。

图3 不同误差相关函数对于相关系数的影响

3 实验结果和对比分析

3.1 不同方案间均方根误差的比较

基于均一化相关尺度方案插值得到的温度场均方根误差剖面如图4，均方根误差如表1。从中可以看出：无论去取何种相关尺度，均一化尺度方案最终的误差都要小于ISAS自带的尺度方案的误差。选用80 km作为尺度半径时，各层的均方根误差分布以及各层平均的均方根误差均是最小，约为1.025℃。随后，计算变形半径方案中各层的均方根误差随深度的变化（见图5）以及各层平均的误差（见表2）。与均一尺度方案类似，变形半径方案中当L＜8R时各层误差以及深度平均的误差均小于ISAS方案，这与前文中关于误差相关尺度不可任意增大的结论是符合的；直接取L＝R时效果并不佳，可能原因是误差相关尺度太小时，分析场所包含的的观测信息太少；当取L＝2R时，整体效果最好，平均误差仅为1.007℃，比ISAS方案降低了0.15℃。

图4 采用均一化相关尺度的各层均方根误差的分布

表1 不同误差相关尺度的插值结果比较——均方根误差

从图4和图5可见，均一尺度方案和变形半径方案各层误差的分布大体类似。以变形半径方案的结果为例分析各层误差特征。如图5所示，无论以何种方式设置误差相关尺度，插值的误差随深度变化均很大，大体上呈现“一大二小”的三峰式分布：即温跃层附近误差最大，上表层和450 m深度处次之，500 m以深误差随深度逐渐减小。上表层属上混合层的范围，温度受到海表感热交换和潜热交换的影响，本身存在一定的日变化，而插值中受制于实测资料数量的局限性，本文的时间窗宽设置为前后15 d，可能因此使得表层误差偏大。在混合层以下温跃层处，由于温跃层内温度变化本身就很大，实测资料的个数占总格点数的比例不超过5%，且实测数据多数是CTD和XBT资料，在温跃层深度并不一定有加密观测，而实测剖面资料在垂向上已经通过Aki ma方法插值到标准层，因此用作检验插值结果的实测数据本身就不一定能够反映温跃层的真实信息，这可能也是温跃层处插值效果较差的原因。在450 m深度附近，多数插值实验均出现一个较弱的误差峰值区，当误差相关尺度设置过大时，误差峰值也越大，这多是因为不合理的误差相关尺度设置造成的虚假信息。在500 m以深的地方，均方根误差随水深逐渐减小，这与海水在下层性质比较稳定、温度变化平缓的特征相吻合。

图5 不同乘积因子的相关尺度的插值结果的各层均方根误差分布

表2 不同乘积因子作用下的误差相关尺度对插值结果的误差影响

整体来看，80～400 m深度（大致位于温跃层内）误差最大，均大于1.2°C。除日本海以外，水深大于400 m的海域多数位于黑潮路径以及副热带环流区域，因此温跃层处的插值误差可能与黑潮有关。根据SODA数据获得135°E断面的流场分布 （图6），黑潮流轴恰好在300 m左右，影响区域大约在450～500 m以浅。因此，500 m以浅的温跃层处的插值误差受黑潮的影响。黑潮与周围水团的水文性质的巨大差异，使得当观测资料较少时，插值的结果无法刻画精细变化，当与实时或准实时的CTD、XBT资料对比时，误差较大。

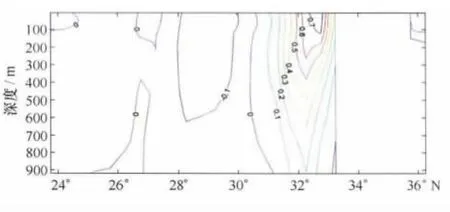
图6 135°E断面的纬向流速（cm／s）分布正值代表流速向东，负值代表流速向西

3.2 不同方案间温度场空间分布的对比

选择各个方案中误差最小的误差相关尺度设置得到的温度场进行分析，并与同时期的SODA资料进行对比，结果如图7。序号1、2、3、4分别代表均一尺度方案（80 km）、ISAS尺度方案、变形半径方案（2倍）和SODA资料在A（50 m）、B（100 m）、C（200 m）和D（460 m）深度处的温度分布。

对于均一尺度方案和ISAS方案，其Mercator格点的表观分辨率（1／2）°×（1／3）°高于SODA 资料（1／2）°×（1／2）°，但是4个典型层次层上的温度场却无法体现SODA资料描述的一些细节，一些中尺度的现象无法分辨出来。均一化尺度方案结果在50 m、100 m、200 m深度处，黑潮附近的水平温度梯度无法体现，尤其是50 m深度处无法刻画黑潮的平流输运作用对于局地温度场的影响；100 m深度处，九州岛东南方向处出现一个小的暖中心（见图7中子图b1）；200 m深度处，均一尺度方案得到的温度场黑潮的平流作用显得过宽，与黑潮实际流幅不符；460 m深度处的均一尺度方案的温度场与SODA相比，暖中心面积更大，不能体现出“一大一小”的双中心配置。在分析各层温度的极小值分布时发现，均一化的尺度方案得到的插值温度场，在有些层次出现了－5.3℃的非正常温度，这表明均一化的误差相关尺度对真实物理场的平滑作用过于强烈，既滤掉很多有用的信息，也无法保证插值结果的可靠性。

分析2倍变形半径作为误差相关尺度时的4个典型层次的温度分布。图中，基于变形半径的尺度方案，可以更好地呈现细节变化。在50 m和100 m深处，在日本四国岛东南方向，存在中心大约位于28°N，136°E的偏冷中心（图7中子图a3和a3），且可一定程度上刻画黑潮对热量的平流输运作用，这与SODA结果（图7中子图a4和a4）类似；而基于均一尺度方案的结果在50 m深度处偏冷中心的位置更偏东南，且中心温度更低；ISAS自带尺度方案在50 m和100 m深度处温度场过于平滑，且在日本以南海域温度偏暖（图7中子图a2和b2）。在200 m深度处，变形半径插值结果与SODA资料相比，均可体现日本列岛沿岸黑潮流经区域水平方向的温度梯度及在琉球群岛附近存在的呈“东北—西南”方向的暖中心区域。但是插值温度场相比于SODA资料，其暖中心偏弱。在460 m深度处，变形半径插值结果可以较好地刻画日本本州岛南侧“一大一小”的暖中心结构，而这是均一尺度方案和ISAS自带尺度方案（图7中子图d1和d2）不能刻画的。因此变形半径方案的插值结果更符合物理规律和客观事实。

图7 不同方案间温度场空间分布对比

在日本以南海域，无论何种分析结果，460 m深度处均存在明显的暖中心，事实上该区域自240～700 m深度处一直存在较强的暖中心。管秉贤［20］处理水文观测资料时发现在伊豆海脊左右两侧存在暖涡。那么该暖中心的维持机制是什么呢？从图8中SODA流场分布来看，该区域自上而下存在着很强的反气旋涡旋。反气旋涡旋，对应海表面海水辐聚，SSH呈现高值中心（见图9）。该海域Argo浮标的温度垂向分布表明，四国海盆海域的温跃层深度大约在150～550 m之间。根据Alexis Chaigneau等［21］关于涡旋三维结构的探究，涡旋的冷暖异常表现在温跃层的深度，因此插值结果中460 m深度处温度场的暖中心主要由涡旋抽吸作用决定。对于50 m和100 m深度处的插值温度场而言，这两层处于上混合层中，从黑潮主轴上脱落的反气旋涡中滞留着来自近岸海域的冷水，从而造成该区域的偏冷现象，其实质是上混合层的温度垂向差异较小，下降流对水平温度分布影响不明显，黑潮流速和涡旋流速对温度场的平流输运起主要作用。变形半径方案中，50 m和100 m深度处的温度场中并未出现如SODA资料中明显的反气旋涡，一方面因为SODA资料是基于数值模式同化的再分析资料，其温度场与流场是相互适应的；另一方面，这两层的温度场同时受到黑潮本身强劲的平流输运作用和反气旋涡的作用，温度分布不完全呈现反气旋涡的形态是合理的。实际上，在该区域200 m深度即黑潮的主轴处，反气旋涡对温度场的影响几乎全部被黑潮掩盖（见图7子图c3和c4）。

图8 日本以南海域各个典型层次上SODA流场（单位：m／s）与基于变形半径的插值温度场（单位：℃）温度场中的等值线依次是20℃（50 m），19.5℃（100 m）以及14.0和13.2℃（450 m）

图9 海表面高度（a），插值温度场（b）和Argo剖面的温度（c）分布

4 小结

提出了基于变形半径计算来改进最优插值中误差相关尺度的研究思想和技术途径，通过与均一化尺度方案及法国ISAS提供的尺度方案的实验比较，得到如下见解：

（1）在实验海域，由于各物理过程的空间尺度极不均匀，变形半径变化复杂，近海约为10 km以内，深海为60 km左右，主要受地形和层结影响；在西边界流海域，主要受黑潮影响，变形半径的空间分布与黑潮流径接近重合。

（2）尽管80 km的均一尺度方案的均方根误差较小，但是其插值温度场无法反应真实环境：一方面是空间尺度较大、温度场过于平滑，另一方面是无法刻画一些重要的物理现象，且温度出现不合理的极值。

（3）相比而言，基于2倍变形半径的相关尺度方案的表现最好：一是均方根误差最小，整体平均为1.007°C；二是能合理刻画该时段四国海盆海域的典型温度分布的三维结构：即上混合层受到涡旋对热量的平流作用在四国海盆区域出现偏冷中心，200 m深度处受黑潮平流输运作用控制，460 m深度的温度场受涡旋抽吸作用控制而表现出暖中心。

（4）需指出的是，当直接采用变形半径作为相关尺度时，插值结果并不理想；当误差尺度设置过大时，如在均一尺度方案中的200 km以及8倍变形半径方案，均方根误差也很大。这说明误差相关尺度不能任意设置，而需有一定的范围。

（5）由于实际海洋中各层次物理过程的尺度存在差异，各层的最优尺度设置也不尽相同。这说明应在不同层次使用不同的误差相关尺度。海洋三维误差相关尺度研究对了解背景场误差协方差矩阵的结构非常必要。

最优插值的目的是利用不规则分布的观测资料获取整个分析区域的海洋资料，以便分析关心海域的动力学和热力学特征，故考虑海洋物理过程对插值结果的调制是必要的。基于此，本文尚存在一些不足和需改进之处：首先是在实验中按Z坐标系垂向分层，除人为将各层误差相关尺度设置为相同值外，在垂向上也是均匀分层，没有考虑温跃层倾斜等问题，这无疑难以考虑更多的物理过程，比如海流的平流输运作用对温度的影响。考虑环流的影响，在海流沿着等密度面运动的区域，如果在将分层设置为等密度面的基础上考虑基于距离的背景场误差相关函数，可能会更好的刻画物理事实。这些问题都有待在进一步的研究中予以考虑和解决。

［1］Talagrand O.Assimilaton of observations，an introduction［J］.J Met Soc Japan，Special Issue，1997，75（1B）：191—209.

［2］Troupin C，Barth A.Generation of analysis and consistent error fields using the Data Interpolating Variational Analysis（DIVA）［J］.Ocean Modeling，2012，52－53：90—101.

［3］Brion E，Gaillard F.ISAS－Tool Version 6：User's manual［R］.France：Ifremer，2012.

［4］闫长香，谢基平，朱江.一个快速海洋三维温盐流分析系统及在亚丁湾邻近海域的应用［J］.气候与环境研究，2011，16（4）：419—429.

［5］Kalnay E.At mosphericmodeling，Data Assimilation and Predictability［M］.Cambridge University Press，2003.

［6］Gandin L S.Objective Analysis of Meteorological Fields［M］.Legingrad：Hydrometeorological Publi，1963.

［7］庄照荣，薛纪善，庄士宇，等.资料同化中背景场位势高度误差统计分析的研究［J］.大气科学，2006，30（3）：533—544.

［8］李冬，王喜冬，张学峰，等.基于扩散滤波的多尺度三维变分研究［J］.海洋通报，2011，30（2）：164—171.

［9］舒业强.针对表层海温与实测温盐的南海海洋资料同化研究［D］.广州：中国科学院南海海洋研究所，2009.

［10］Jacob L，Høyer，Jun She.Opti mal inter polation of sea surface temperature for the North Sea and Baltic Sea［J］.Journal of Marine Systems，2009，65（1－4）：176—189.

［11］Meyers C，Phillips H，Smit h N，et al.Space and time scales for optimal interpolation of temperature－Tropical Pacific Ocean［J］.Prog Oceanog，1991，28（3）：189—218.

［12］Reynolds，Richard W，Dudley B.Chelton comparisons of daily sea surface temperature analyses for 2007－08［J］.J Cli mate，2010，23：3545—3562.

［13］Qiu Bo.Kuroshio extension variability and forcing of the Pacific decadal oscillations：responses and potential feedback［J］.J Phys Oceanogr，2003，33：2465—2482.

［14］LeBlond P H，Mysak L A.Waves in the Ocean［M］.Ar msterdam∶Elsevier，1978.

［15］Pedlosky J.Geoptysical fluid dynamics［M］.New York：Springer－Verlag，1987：710.

［16］Gill A E.At mosphere－ocean Dynamics［M］.New York：Academic Press，1982.

［17］Emery W J，Lee W G，Magaard L.Geographic and seasonal distributions of Brunt－Vaisala frequency and Rossby radii in the North Pacific and North Atlantic［J］.J Phys Oceanogr，1984，14：294—317.

［18］Chelton，Dudley B，Roland A，et al.Geographical variability of the First Baroclinic Rossby Radius of deformation［J］.J Phys Oceanogr，1998，28：433—460.

［19］Cai Shuqun，Long Xiaomin，Wu Renhao，et al.Geographical and mont hly variability of the first baroclinic Rossby radius of deformation in the South China Sea［J］.Journal of Marine Systems，2008，74（1／2）：711—720.

［20］管秉贤.伊豆海脊两侧顺时针流涡的若干观测证据［J］.海洋科学进展，1996，14（4）：1—9.

［21］Chaigneau A，Texier M L，Eldin G，et al.Vertical structure of mesoscale eddies in the eastern South Pacific Ocean：A composite analysis from altimetry and Argo profiling floats［J］.J Geophys Res，2011，116（C11）：25.