海表Ek man流不稳定性致新型次级环流
李燕,乔方利,戴德君,马洪余
(1.中国海洋大学 物理海洋实验室,山东 青岛266003;2.国家海洋局 第一海洋研究所 海洋环境科学和数值模拟国家海洋局重点实验室,山东 青岛266061)
1 引言
在流体力学中,次级环流又称为二次流。二次流是指在主流动区域内所出现的一种与主流性质不同的从属流动,产生原因复杂,表现形式也各不相同[1]。次级环流是流体力学领域的重要研究方向,本文主要针对海洋上层发生的次级环流进行介绍。海洋上层次级环流是一种重要的海洋动力学现象,与海洋生态、海洋灾害、海洋遥感、混合过程等都有着密切联系,我们可以从很多现象中找到其存在的旁证。海洋中偶然出现的表层漂浮物可以看作次级环流的示踪物,让我们清楚地看到它们的存在。图1为2008年青岛浒苔暴发期间所摄照片,照片中可以明显的看到浒苔呈条带状分布,浒苔聚集的地方应该是次级环流的辐聚区。此外,2010年美国墨西哥湾原油泄漏时卫星所摄图片(见图2)中同样可以清楚地看到这种条形油膜的存在。除了在海洋中,大气中类似的环流形式也是普遍存在的,即我们所熟知的云街现象,它是一种积云或者属于积云之类的云在天空中平行排列的情形。
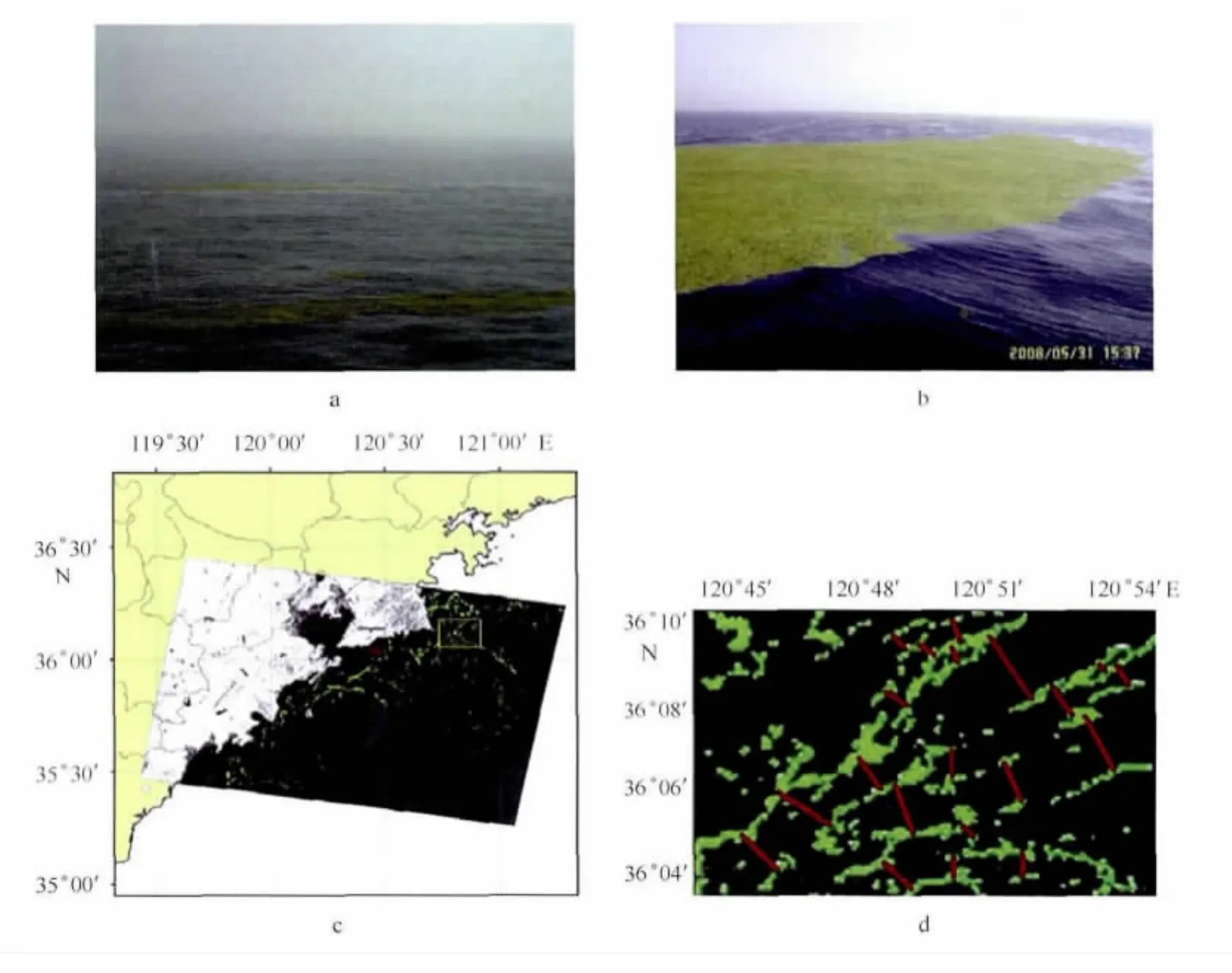
图1 海面漂浮浒苔的带状分布结构
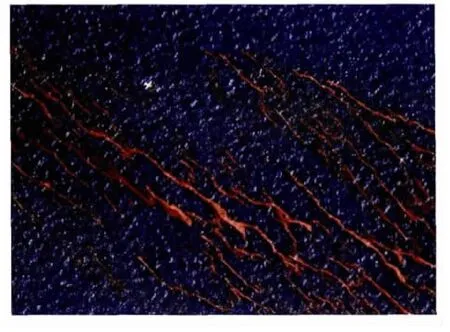
图2 墨西哥湾原油泄漏事件溢油油膜分布:锈迹斑斑的漂带
在大气科学中,20世纪60—70年代,为解决行星边界层中次级环流的问题,Lilly[3-4]以及 Brown[5]成功的解释了云街现象,丰富了大气行星边界层理论。他们认为云街现象是由于大气边界层流动的动力不稳定性造成的,并利用流体运动不稳定理论方法分析扰动增长率,从而确定最易成长的不稳定状态,由此所得出的次级环流在尺度上与观测结果有很好的一致性。不同于Lilly的是,Brown在1970年的工作中考虑了温度层结的存在,并指出经常发生在大气和海洋边界层中的涡旋的特征深度约是Ek man特征长度的5~7倍,相关的波长约为Ek man特征长度的4π倍。
海洋中,次级环流的研究大部分集中于海洋的边界层区域和具有特殊流场结构的区域。Qiao利用不稳定理论研究了切变波的形成机制[6],袁业立等[7]利用摄动分析方法,基于观测的流速分布特征提出了一种黑潮多核结构的不稳定形成机理,解释了东海黑潮的多核结构现象,与观测有着良好的一致性。对于海底或湖底的边界层,很多研究认为次级环流的产生和维持与底形的存在有很大的关系。1997年董昌明在其博士论文中运用稳定性分析方法获得了主流场的最不稳定状态,得出由潮流诱生的次级环流与潮流沙脊的成因有内在的因果关系[8],避免了前人解释沙脊成因时必须首先假定底形的先决条件[9-10],丰富了海底沙脊形成机理的认识。对于海表边界层的次级环流,我们比较熟知的是Langmuir环流,也是目前研究者相对比较关注和研究较多的。1927年,当Ivring Langmuir乘船横越大西洋从美国去英国的途中,发现海面上存在规则间隔的长而窄的海草及海面漂浮物所构成的漂浮带,这些漂浮带以平行于海风的方向排列并且随着风向的转变而重新排列。他意识到一个局地的辐聚是产生漂浮带的一个必要条件,而从质量守恒推断,会在漂浮带以下存在一个下降运动,并一定会存在一个补偿的上升运动。关于这类环流存在的想法被Langmuir在George,NY湖上进行的简单但精巧的实验得到验证。此后众多学者对这一现象进行了研究[11-17]。就目前的观测和理论研究结果看,Langmuir环流的尺度主要集中于几米到几百米的量级[18-21]。
对于海洋表层的次级环流,除去Langmuir环流之外,Qiao等[2]在2008年浒苔暴发期间观测到漂浮浒苔在海面基本呈条带状分布,条带的长度从几百米到几十千米不等,条带之间的距离大多集中在1~1.5 k m。这样的条带之间距离远大于之前所报道的由Langmuir环流所造成几米到几十米的条带间距。Thorpe[22]认为这是由小尺度的Langmuir环流条带逐步合并形成的,并提出一个理想模型模拟其合并过程。若单从浒苔条带状的分布结构上来看,其水平尺度与董昌明、Lilly等学者利用线性稳定性方法所得的次级环流尺度类似。乔方利等[23]曾利用MASNUM业务化数值模式的预报结果在南黄海西部 (35.0°~37.0°N,119.2°~122.0°E)区域对风向与表层海流流向之间的关系进行了统计,认为即便是在近海区域,表层流场与风之间也与经典的Ek man漂流理论符合较好。本文认为浒苔条带状结构分布的成因应该与Ek man流的不稳定性所造成的次级环流直接有关。下面将利用稳定性分析的方法对海洋表层次级环流的生成机制及其尺度特征进行分析。
2 海洋表层次级环流诱生理论
2.1 流体运动基本控制方程
海水运动基本控制方程包含连续性方程和动量方程如下:
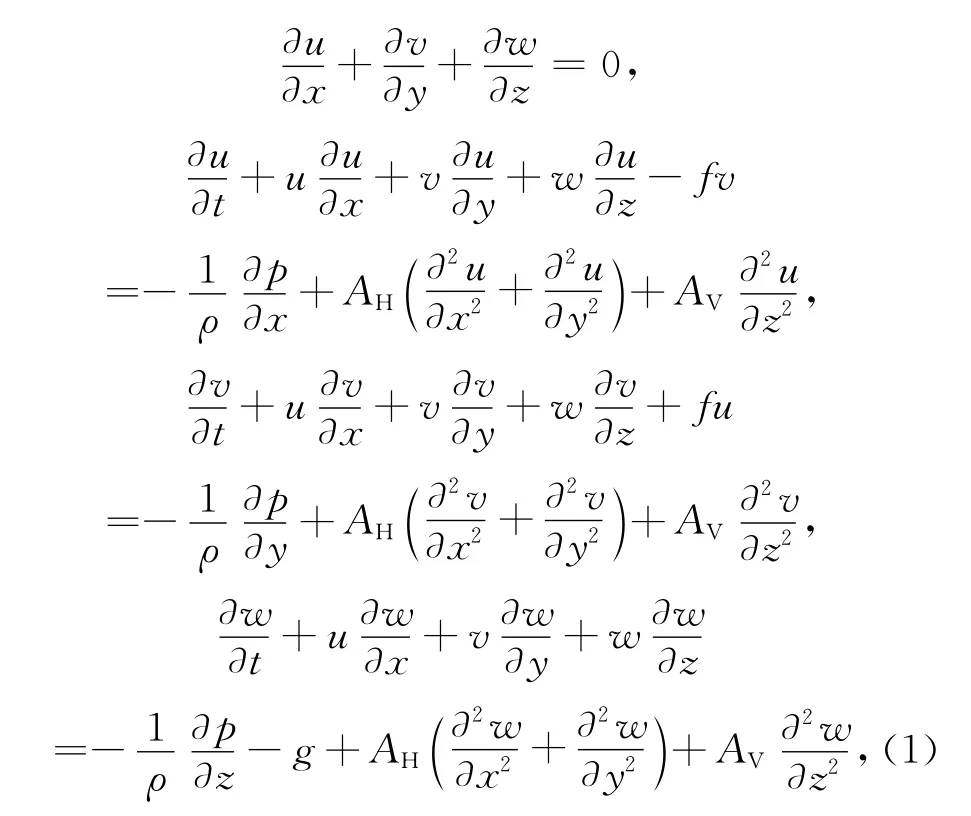
式中,u、v、w分别为速度矢量在x,y,z方向上的速度分量;f为科氏参数;p和ρ分别为流体的压力和密度;g为重力加速度;AH为水平湍黏性系数,AV为垂向湍黏性系数,这里均取为常数。
由于我们关心发生在海表面的现象,故上下边界条件取为如下形式,假定下边界流速为零,海表主要受风应力影响:
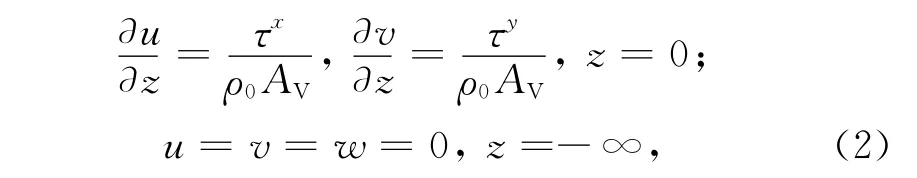
式中,ρ0为海水密度,τx和τy分别为x和y方向的风应力。
为了得到扰动控制方程,我们将u,v,w,p写成系统平均量和脉动量两部分之和,带“—”的为平均量,带“*”的为脉动量,则:
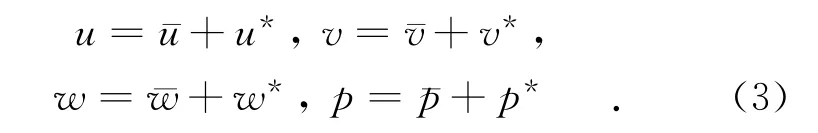
将式(3)代入式(1)可得扰动量控制方程为:


同时得到扰动量控制方程边界条件为:

由此便得到了由式(4)和式(5)所组成的扰动控制方程组,这也是以下分析的基础方程。
2.2 主流场结构
本文关注海洋上层次级环流的生成机制,故主要针对海表边界层的流场结构进行分析,取风生Ek man漂流为主流场。同时,考虑到次级环流的尺度不大,因此我们取f平面,即不考虑科氏力随纬度的变化,且假定水平与垂直湍黏性系数AH、AV为常量。我们考虑稳定状态下的流场结构,故略去时间导数项。按照上述的假定,海水运动方程可简化为如下方程:

边界条件如下:

式中τx和τy分别为x和y方向的风应力。从而可得到主流场流速剖面为:
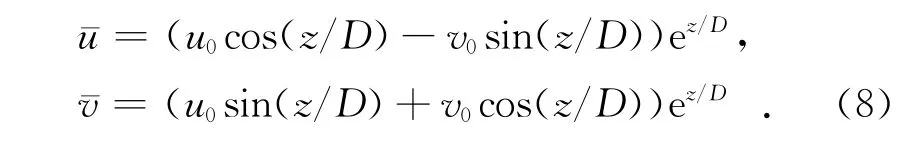
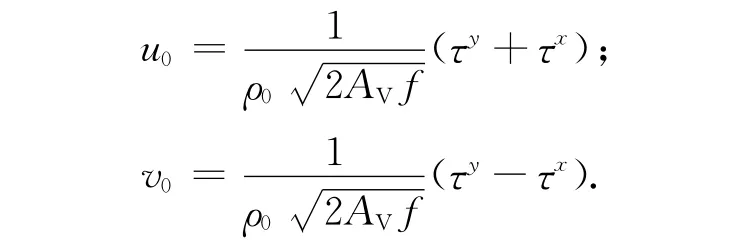
由于只关心主流场的垂向结构,因此我们并不关心u0和v0的具体取值。在不影响结果分析的前提下,假设v0=0,即主流场结构为
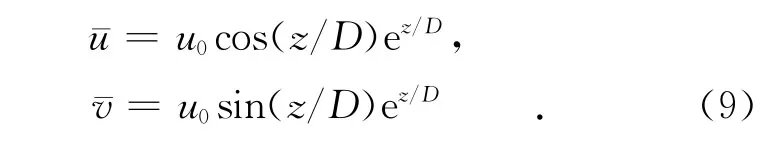
以上流速剖面是在理想假设条件下取得的,而在实际中,流场结构将会受到很多因素的影响。参考董昌明[8]的做法,引入一个调整因子r,将主流场流速结构修正为:

当r=1时,即是式(9)所示的经典海表Ek man流的情况。在现实海洋中,实测流速的垂直变化要比Ekman流缓和一些[8],故我们在随后的数值试验中将r的取值范围确定为0<r≤1。
为了更清楚的看到本文中所研究的现象特征,在图3中给出了调整因子r在不同取值情况下式(10)所表示的主流场结构图,其中均以北半球为例,r取值分别为1.0,0.8,0.6,0.4。从图3中可以看出调整因子r代表了主流的衰减速率,r的值越大,则主流衰减越快,对应的流速剪切也越大;反之,r值越小,则主流衰减越慢,对应的流速剪切也越小。
2.3 次级环流
类似于Langmuir环流,次级环流流场与主流场之间往往存在一个偏角[7,15]。由于我们的着眼点是次级流动,为讨论方便,将坐标轴逆时针旋转θ角,使旋转后的新坐标轴x′与次级环流的主轴走向一致,这样次级环流在新坐标系中仍为二维流动。同时,分别以D,u0,D/u0分别作为空间、速度和时间尺度,无量纲化上述变量可得:

u′,v′,w′,p′,u,v均为新坐标下的无量纲物理量,其中带“′”号的为扰动量,没有的为平均量。同时,由于在新坐标系下次级环流为二维流动,各扰动量在x′方向均匀,故沿x′方向上的导数为零,即=0。由于=0,故在y、z平面内二维无辐散,为研究问题的方便,可引入流函数ψ′:

因此,新坐标系下的无量纲方程为:
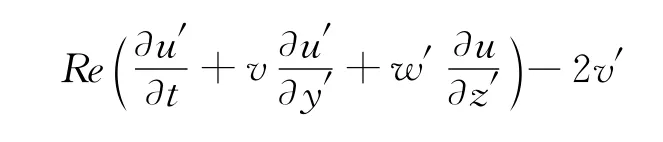
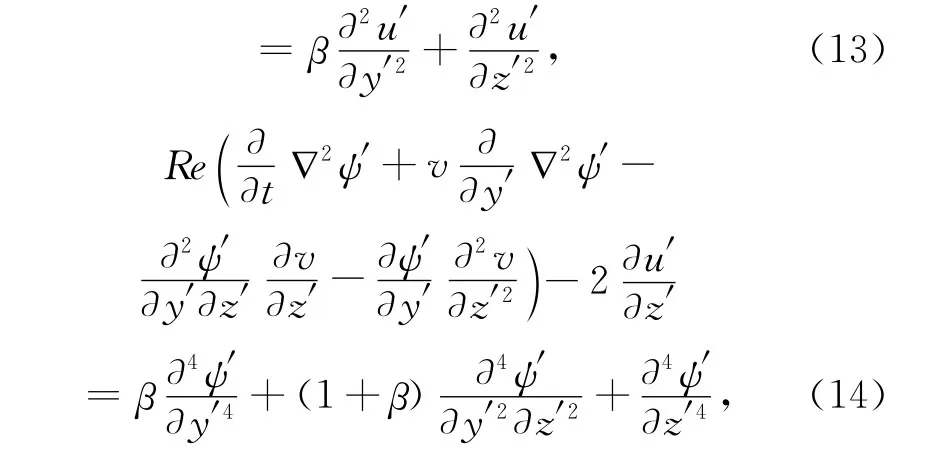
式中,Re=u0D/AV,β=AH/AV。
按照不稳定性分析的基本思路,需要分析满足方程(13)和(14)的解随时间变化的情况。如果当t→∞时,所有可能的解都趋近于零,则原来的层流就是稳定的,而只要有一个解不满足这一条件,则原来的层流就是不稳定的。由于方程(13)和(14)的系数仅与z有关,所以扰动形式可设为

式中为复振幅,a为波数。由于我们的着眼点是看扰动随时间的演化,即时间模式问题,故将a取为实数。ω为复数,ω=ωr+iωi。将式(15)代入式(13)和(14)可得特征方程为:


图3 不同调整因子(r=0.4,0.6,0.8,1.0)下的主流场结构图
边界条件转化为:

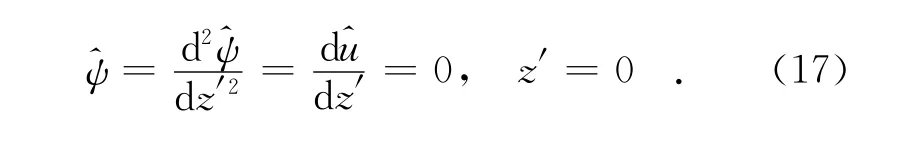
由于方程(16)及边界条件(17)都是齐次的,要求非零解(零解相当于无扰动),其参数Re、a、θ、ω、β就必须满足一定的函数关系
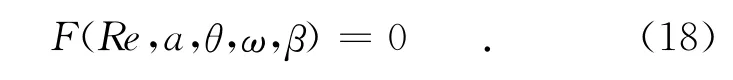
式(18)称为特征关系。即如果给定了Re、a、θ、β的数值,就可求得复特征值ω。当ωi>0时,扰动的模将增长,原来的层流就是不稳定的;当ωi<0时,扰动将衰减,层流是稳定的;若ωi=0,扰动的模不变,称为中性解。求解上述特征值问题的解析解是十分困难的,因此我们采用数值解法。方程中用到的差分格式如式(19)所示,其中k为计算值的网格点标号,Δz′为网格间距。数值计算时,网格设置自变量在z′的离散的整网格点上在半网格点上。

3 数值模拟结果和分析
本节将针对水平与垂直湍黏性系数相等与不等这两种情况对数值模拟结果进行分析。
3.1 水平与垂直湍黏性系数相等的情况(β=1)
分析分别针对表1中不同的雷诺数Re、调整因子r、波数和偏角θ。

表1
同时针对南半球和北半球,本文进行了一系列的数值实验,结果如下。
先以北半球为例,图4给出了在不同的调整因子(r=0.2,0.4,0.6,1.0)情况下复特征值ω的虚部部分ωi的分布情况。由前文可知,当ωi>0时,扰动的模将增长,原来的层流不稳定;当ωi<0时,扰动将衰减,层流是稳定的;若ωi=0,扰动的模不变,称中性情况。从图4中可以看出,对于不同参数下的特征值分布各具特点,但复特征值的虚部最大值基本集中在0.006以上,这个数值表征了扰动增长快慢的尺度,也就是说扰动增长的时间T=1/ωi<1/0.006≈167。根据前文无量纲化的标准T=D/u0,假设D=40 m,u0=1 m/s得出有量纲的时间约为6 660 s,即时间为小时量级。此外,图4中以r=0.6分图为例进行说明,随着雷诺数Re的增加,不稳定的状态范围逐渐增大,其中最不稳定的状态的波数逐渐增大,偏角也逐渐增大,总体范围集中在5°~35°之间。对于其他调整因子的情况也呈现出基本类似的规律。
除此之外,我们考虑一下计算所得次级环流的空间尺度。从图4中可以看出对于相同雷诺数的情况下,r越小,最不稳定的波数越小,波长越长。而对于相同调整因子r的情况下,雷诺数越小,最不稳定的波数越小,波长越长。同时最不稳定的波数范围集中在0.2~1.5之间,由此可以计算得到波长为λ=2π/a·D(其中a为波数)。考虑在现实海洋中的情况,若取D=40 m,则计算可得波长范围在160~1 250 m之间。
为了更清楚地看到所生成次级环流的特征,图5给出了雷诺数Re=600,波数为1.2,偏角20°,调整因子r分别取值为0.4,0.6,1.0时的主流场和次级环流的流函数分布。计算过程中ω的虚部ωi的值对应于上述调整因子分别为0.002 7,0.003 7,0.004 1。从图5可以看出很明显的对称型次级环流的存在。另外,对于不同的调整因子,次级环流的垂直位置有相应变化,调整因子r的取值越大,则生成的次级环流越靠近表面,随着调整因子r的取值增大,次级环流的位置有逐渐下移的趋势。
此外,为考虑科氏力的作用,下面我们给出南半球的情况,具体推导过程不再给出,图6中直接给出数值模拟结果。特征分布基本与北半球呈现相同的变化规律,唯一不同的是次级环流与主流场的偏角发生了变化,北半球次级环流的流轴与主流场夹角为正值,而南半球次级环流的流轴与主流场夹角为负值,大小基本没什么变化。

图4

图4 不同调整因子下(r=0.2,0.4,0.6,1.0)的复特征值的虚部等值线图(北半球)

图5 不同调整因子(r=0.4,0.6,1.0)下的主流场速度(左图)及次级环流流函数分布(右图)
3.2 水平与垂直湍黏性系数比值对数值模拟结果的影响(β≠1)
为考虑最不稳定的特征值所对应的波数和偏角与水平与垂直湍黏性系数比值β(AH/AV)之间的关系,图7和8中分别给出了雷诺数Re和调整因子r在不同取值组合下的最不稳定状态特征值ωi和偏角与β之间的分布。可以看出,不论雷诺数Re和调整因子r的取值如何变化,随着β的增大,最不稳定状态所对应的波数都呈现迅速减小趋势,当β≥100以后,波数都减小到0.1以下,此时对应的波长为2 k m左右,此后基本不再变化。也就是说,β越大,由Ek man流不稳定性导致的次级环流的水平空间尺度越大。
对于次级环流轴线与主流场的偏角,随着β的增大,偏角的变化规律较为复杂,r的取值较小时,呈现单调的减小趋势,并且没有符号的变化,即仍然是在北半球偏向主流左侧;但是当r的取值较大时,变化规律不再是单调趋势,而是时增时减,而且会发生符号的改变,即在北半球出现偏向主流右侧的情况。
Smith[24]曾给出Langmuir环流的示意图(见图9),从其给出的模型中可以看出Langmuir环流的轴线偏向风向右侧5°~15°,而理想Ek man流偏向风向右侧45°左右,这也就说明北半球Langmuir环流的轴线偏向Ek man流的左侧,表明从偏角看,Langmuir环流与我们分析得出的Ek man流不稳定产生的次级环流有共性之处。但是当考虑到水平与垂直湍黏性系数比值β时,随着β的增大,Ek man流不稳定产生的次级环流空间尺度逐渐变大至千米量级,与观测的黄海浒苔间距基本一致。这也从一个侧面表明Ek man流不稳定产生的次级环流是一种新的次级环流。
4 讨论
无论是海气相互作用还是海洋动力过程,海洋上混合层都是十分重要的。海洋上层的次级环流虽然属中小尺度环流系统,但它对海洋的垂直混合和物质的垂向输运有重要影响。同时,由于条带所在处正是一对环流形成的辐聚带,由此也可推断,不仅是漂浮物,其他物质也有可能在此处形成聚集,因此它既可以是生物高生产力区,也可能是高污染区。这一环流的存在对海洋环境保护和海洋生态系统的影响也是显而易见的,对海洋灾害防治如藻类防治、溢油灾害等方面有重要的实际意义[25-26]。
本文利用线性稳定性理论,研究了海洋上层Ekman流的不稳定性,从本文数值结果来看,当背景流场为Ek man流时,若雷诺数大于100时就会出现相应的不稳定状态,从而出现次级环流。由Ek man流不稳定性所导致的次级环流具有相当大的空间和时间尺度范围,其尺度大小与雷诺数、Ek man流的衰减速率和水平与垂直湍黏性系数比值等都有密切关系;另一方面,真实的海洋中水平湍黏性系数与垂向湍黏性系数的准确量值很难确定,对于海洋环流现象,水平尺度比垂向尺度要大得多,通常在数值模式中选取的水平黏性系数要远大于垂向黏性系数。但就Langmuir环流而言,由于其水平尺度和垂向尺度相差不太大,在关于Langmuir环流的文献中,经典理论都是将垂向与水平黏性系数取为相同数值[12-13]。因此讨论水平与垂直湍黏性系数比值实际上也反映了物理现象的空间尺度。如果我们参照以往取法[11-12]即二者相等,从本文数值结果来看,所得出的次级环流结构、空间尺度以及次级环流流轴与主流场偏角都与Langmuir环流的特征极为相似,因此这应该可以作为Langmuir环流形成机制的一种新解释。
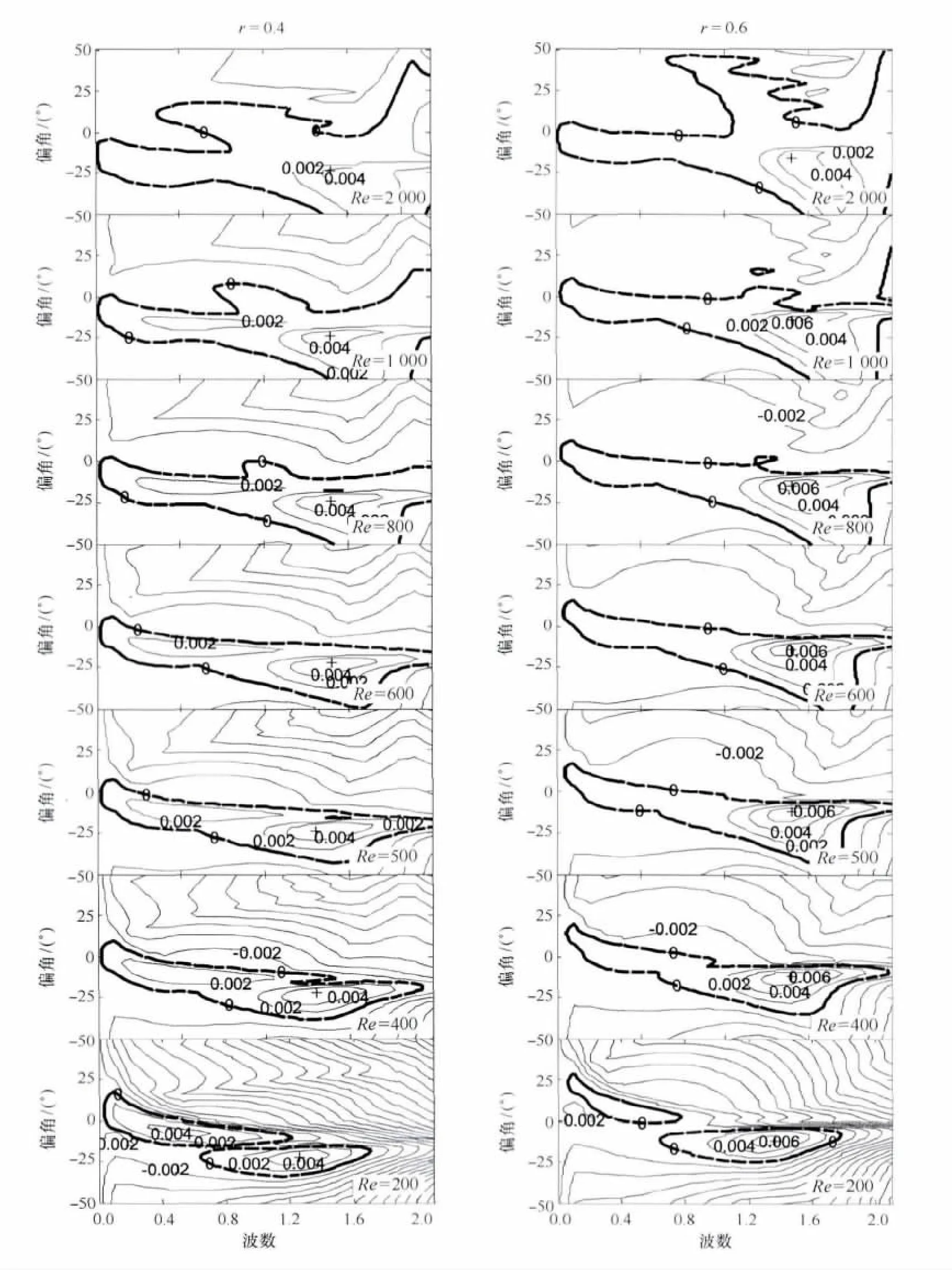
图6 不同调整因子下的复特征值的虚部等值线图(南半球)
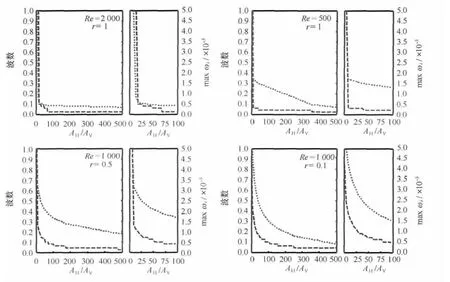
图7 不同雷诺数和调整因子下,水平与垂直湍黏性系数比值(A H/A V)对波数(wave number)的影响

图8 不同雷诺数和调整因子下,水平与垂直湍黏性系数比值(A H/A V)对偏角的影响
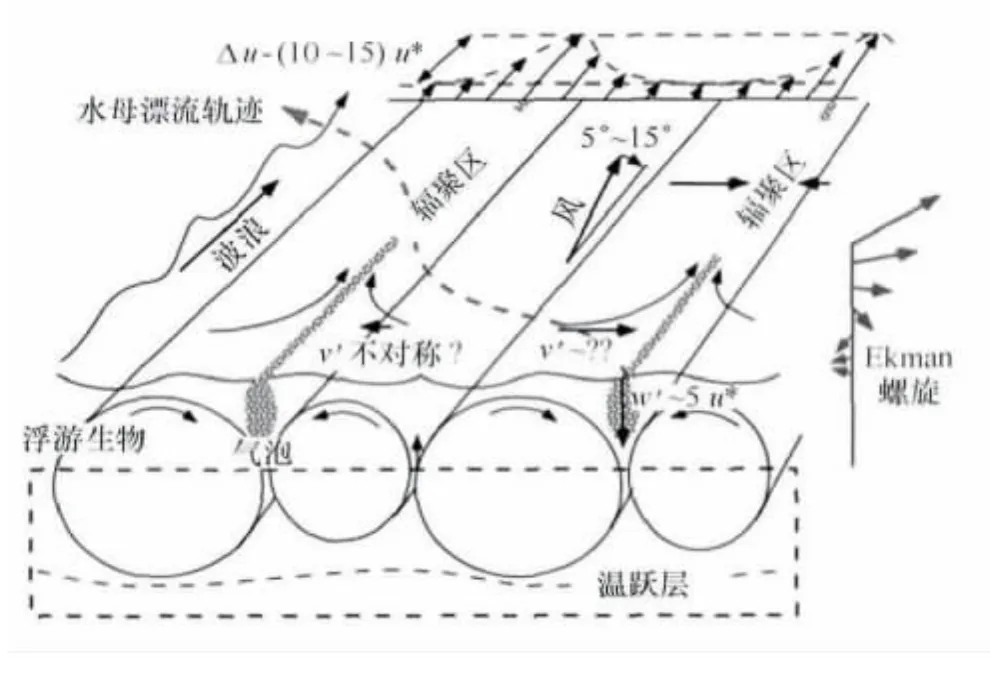
图9 Langmuir环流的示意图(引自文献[24])
当水平湍黏性系数与垂向湍黏性系数取值不同时,由Ek man流的不稳定性所生成的次级环流尺度可达到千米量级,其尺度范围明显大于前人所报道的Langmuir环流几百米以下的空间尺度,而这应该是Qiao等[21]所提出的浒苔条带状结构的成因。但我们目前仍缺乏系统翔实的观测资料,可以支撑更为深入细致的研究,比如精密的卫星资料可以确定黄海浒苔条带间距是否随纬度升高而增加,从而判别Thorpe的模型是否合理。从目前可获取的资料来看,我们更倾向于认为对应于Ek man流的不稳定性,存在一种新的次级环流。
[1]湛含辉,成浩,刘建文,等.二次流原理[M].长沙:中南大学出版社,2005:1-33.
[2]Qiao F L,Dai D J,Simpson J,et al.Banded structure of drifting macroalgae[J].Marine Pollution Bulletin,2009,58(12):1792-1795.
[3]Lilly D K.On the computational stability of numerical solutions of time-dependent non-linear geophysical fluid dynamics problems[J].Monthly Weather Review,1965,93(1):11-25.
[4]Lilly D K.On t he instability of Ek man boundary flow[J].Journal of At mospheric Sciences,1966,23:481-494.
[5]Brown R A.A secondary flow model for the planetary boundary layer[J].Journal of t he At mosphere Sciences,1970,27:742-757.
[6]Qiao F L.Instability analysis of three-di mensional ocean shear waves[J].Acta Oceanologica Sinica,1996,15(1):1-8.
[7]袁业立,万振文,张庆华.东海黑潮多核结构的运动不稳定性形成机理[J].中国科学D辑:地球科学,2002,12:1011-1019.
[8]董昌明.潮流沙脊成因的流体动力学研究及其卫星遥感分析[D].青岛:中国科学院海洋研究所,1997:27-51.
[9]Colombini M.Turbulence-driven secondary flows and for mation of sand ridges[J].Journal of Fluid Mechanics,1993,254(1):701-719.
[10]Huthnance J M.On one mechanism for ming linear sand banks[J].Estuarine,Coastal and Shelf Science,1982,14(1):79-99.
[11]Langmuir I.Surface motion of water introduced by wind[J].Science,1938,87:119-123.
[12]Craik A D D.A wave-interaction model for the generation of windrows[J].Journal of Fluid Mechanics,1970,41(4):801-821.
[13]Craik A D D,Leibovich S.A rational model for Langmuir circulations[J].Journal of Fluid Mechanics,1976,73(3):401-426.
[14]李爽.Langmuir环流和波浪破碎对上层海洋混合影响的数值研究[D].青岛:中国科学院海洋研究所,2010:1-40.
[15]Noh Y,Min H S,Raasch S.Large eddy si mulation of the ocean mixed layer:The effects of wave breaking and Langmuir circulation[J].Jour nal of Physical Oceanography,2004,34(4):720-735.
[16]Mc Williams J C,Sullivan P P,Moeng C H.Langmuir turbulence in the ocean[J].Journal of Fluid Mechanics,1997,334:1-30.
[17]Skyllingstad E D,Denbo D W.An ocean large-eddy simulation of Langmuir circulations and convection in the surface mixed layer[J].Journal of Geophysical Research,1995,100(C5):8501-8522.
[18]Leibovich S.The for m and dynamics of Lang muir circulations[J].Annual review of fluid mechanics,1983,15(1):391-427.
[19]Pollard R.Observations and theolies of Lang muir circulations and their role in near surface mixing[J].A Voyage of Discovery:1977,70:235-251.
[20]Thorpe S A.Lang muir circulation[J].Annual Review of Fluid Mechanics,2004,36:55-79.
[21]Smith J A.Observed growt h of Langmuir circulation[J].Journal of Geophysical Research,1992,97(C4):5651-5664.
[22]Thorpe S A.Spreading of floating particles by Langmuir circulation[J].Marine Pollution Bulletin,2009,58(12):1787-1791.
[23]乔方利,王关锁,吕新刚,等.2008与2010年黄海浒苔漂移输运特征对比[J].科学通报,2011,56(18):1470-1476.
[24]Smith J A.Observations and t heories of Langmuir circulation:a story of mixing[J].Fluid Mechanics and the Environ ment:Dynamical Approaches,2001:295-314.
[25]GuadayolÒ,Peters F.Analysis of wind events in a coastal area:a tool for assessing turbulence variability for studies on plankton[J].Scientia Marina,2006,70(1):9-20.
[26]Thorpe S A.Langmuir circulation and the dispersion of oil spills in shallow seas[J].Spill Science &Technology Bulletin,2000,6(3/4):213-223.

