水平管道内冰浆流动阻力特性实验研究

王继红，王树刚，张腾飞，贾廷贵

(大连理工大学建设工程学部，辽宁大连116024)

区域供冷作为一种新型能源基础设施建设策略，近年来受到广泛关注。为全面提升区域供冷系统冷量输送效率，尝试采用新型相变流体代替传统载冷介质，是实现区域供冷系统经济性投运的理想途径。冰浆是一种新型相变流体，其区别传统载冷介质冷冻水的主要特征是，浆体是由冰粒子和载流体构成的固液混合物，具有良好的热物性、传输性及相变特性［1］。因此，在区域供冷系统内推广使用冰浆作为载冷介质，将会使系统的冷量输送效率得到明显改善［2-3］。然而，作为冰浆介质工程推广的基础性研究，对于冰浆在流动过程中所表现出的流变特性和阻力特性仍亟展开深入研究。

现有关于冰浆流动特性的研究，主要集中于小尺度管道的冰浆流变及阻力特性的研究［4-7］。但冰粒子时变特性及其与载流体间的密度差异［8］，使得冰粒子在管道内流动时需要一个稳定过程，同时管道截面尺寸的变化亦会对冰粒子的浓度分布产生影响。由此可见，放大冰浆流动的管道尺度，将有助于再现冰浆流体在工程应用时的真实流动特性。鉴于此，本文将采用实验测试的研究方法，借助固液两相流非牛顿流变理论和单相流理论，研究了长距离输送管线内，当浆体处于不同的输送速度、不同的冰粒子浓度及不同的管道直径时浆体所表现出的流变特性和阻力特性。

1 实验方法

1.1 实验装置简介

如图1所示，冰浆输送实验系统主要由3个子系统构成，即:冰浆存储系统、冰浆输送系统及参数监测采集系统。其中，冰浆存储系统是由容积为0.5 m3的保温罐体和搅拌装置组成，可为输送系统提供均质冰浆。冰浆输送系统是由浆体泵、输送管线(管长L≈100 m)及流量调节装置组成，可实现输送系统的变工况运行。参数监测采集系统是由监测设备及数据采集仪组成。在实验测试过程中，主要监测参数为浆体温度、密度、质量流量、测试管段的压降。其中，数据读取借助于数据采集系统自动记录。各监测设备概况如表1所示。

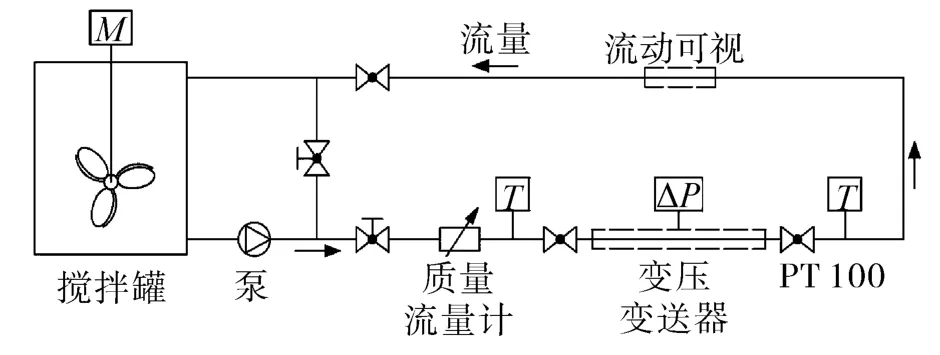
图1 冰浆输送实验系统Fig.1 Schem atic diagram of the experimental set-up

表1 主要监测设备列表Table 1 List of main measuring instrument

1.2 实验测试过程

在实验中，冰浆的制备是在恒温恒湿气候室内完成(室温Tc=-10°C)。为提高冰浆流体的传输性及制备的经济性，目前业界围绕冰浆流动特性所展开的研究中，通常是选取粒径小于1 mm的冰粒子和具有冰粒子凝固抑制作用的水溶液所构成的固液混合物作为研究对象的［1］。因此，本文在实验中所制备浆体亦是由直径小于1 mm的冰粒子和11%的乙醇溶液组成，如图2所示。借鉴水沙两相流的流动过程不难发现，当固相颗粒直径增大时，两相流的非均质性流动过程增强［9］。因此，为了减弱冰浆流体中冰粒子在流动过程中的非均匀分布，在实验中冰粒子的粒径由筛网控制在1 mm以下。

图2 实验用冰粒子及冰浆流体Fig.2 Photo of the artificial ice particles and ice slurry

对于所获得的冰浆，其冰粒子的浓度是通过测量浆体及其各组分的密度间接获得［10］

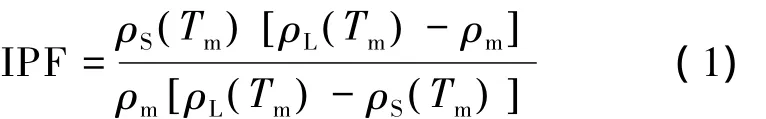
式中:IPF表示冰粒子浓度，即质量浓度;T表示流体温度，°C;ρ表示流体密度，kg·m-3;S、L、m 分别表示固体颗粒相、液体载流体相和浆体混合相。

实验系统的输送管线、阀门及测试装置均采用保温材料保温。通过对流经压降测试管段进出口流体温度监测发现，在压降测试时段内，温度变化并不明显。因此，可将本文所研究的流动工况近似为等温流动，即在测试过程中冰粒子的浓度保持不变。各测试工况相关的具体信息，如表2所示。

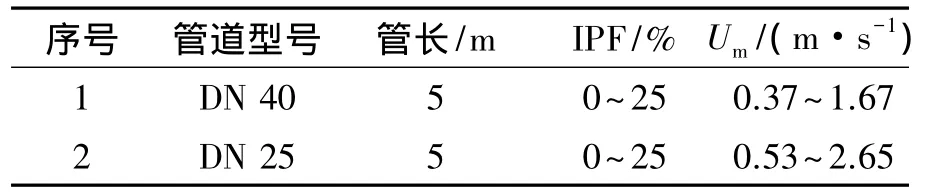
表2 测试工况分布Table 2 Operating conditions

2 实验结果

2.1 冰浆流变模型

冰浆作为固液两相流体，其流变特性会随着冰粒子浓度的改变而变化。为确定冰浆流动的流变特性及阻力特性，通常需建立管壁切应力与剪切速度间的关系:

式中:τW表示管壁切应力，Pa;γW表示管壁剪切速度，s-1。

对于管壁切应力，当流体流过水平管道时，其与管道压降之间始终满足如下关系:

式中:D表示管道直径，m;L表示管道长度，m;ΔP表示管道压降，Pa。

管壁剪切速度是与流体的流变参数密切相关的。通常，对牛顿流体而言，其管壁剪切速度［11］为

式中:Um表示平均流速，m·s-1;γW，New表示牛顿流体管壁剪切速度，s-1。

在式(3)和(4)中，D、L、ΔP、Um均为实验中较易直接或间接测得的物理参数。因此，根据实验测试结果，即可通过式(3)和(4)直接确立出牛顿流体的本构关系。但对非牛顿流体来说，由于式(4)并不足以刻画出流体在壁面处的剪切速度，因此，仅仅利用式(3)和(4)无法直接获得流体流变特性。通常，借鉴牛顿流体的研究方法，首先建立式(3)和(4)间的关系，再进一步确立流体的流变特性。

对于冰浆而言，其区别于牛顿流体的线性流变规律，可表现出幂律流体的流变特征［6］，即:式(3)和(4)之间满足指数变化规律:

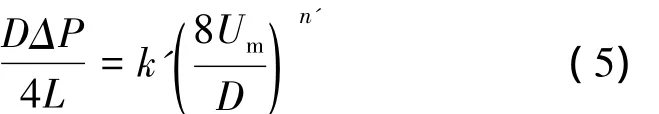
根据幂律流体的流变模型［12］，其管壁切应力与剪切速度间满足幂律关系:

式中:k表示流变系数，Pa·s;n表示流变指数;γW，Non表示非牛顿流体管壁剪切速度，s-1。

为了进一步确定 n、k与 n＇、k＇间的关系，需借助平均流速Um随切应力τ的变化规律［13］:

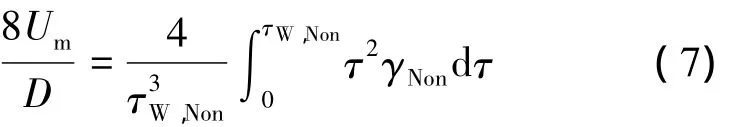
根据式(5)～(7)，冰浆的流变指数、流变系数及管壁剪切速度可分别表示为

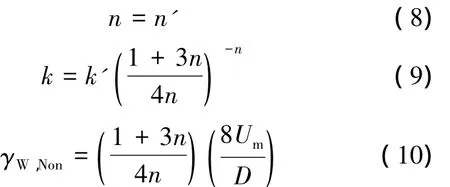
在此需要特别指出的是，通常基于上述方法确定冰浆的流变特性时，只适用于层流流动状态。对于冰浆的圆管湍流流变特性计算，目前还没有成熟的计算方法［11］。因此，当冰浆处于湍流区域内流动时，其流变参数n、k与n＇和k＇间的转换亦会参照层流流动时的转换方法，如文献［5］。

2.2 管道内冰浆流动压降模型

在冰浆管道流动中，流态变化会对冰粒子浓度分布产生一定影响。因此，对应不同流态区域，冰浆流动阻力特性也会存在显著差异。在此，为判别浆体运动时所处的流态区域，引入广义雷诺数。基于广义雷诺数，可分别对处于层流区域和湍流区域内的冰浆流动阻力系数进行计算［11］:

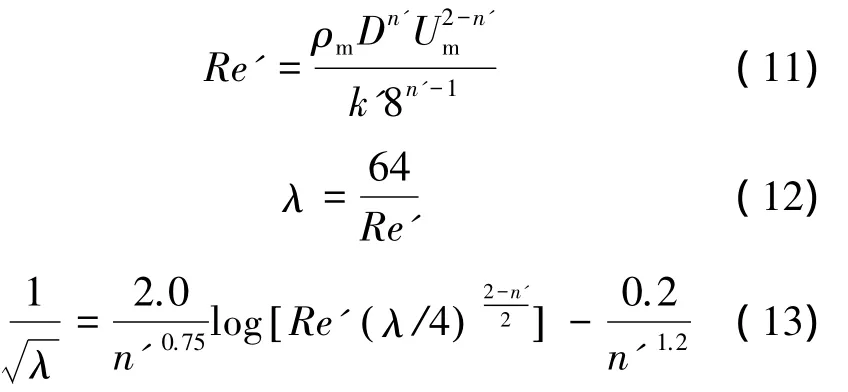
式中:Re'表示广义雷诺数，λ表示流动阻力系数。

需要指出的是，在冰浆流动中，由于冰粒子间及冰粒子与载流体间相互作用的复杂性，使得对于冰浆流动的流态判别尚缺乏统一的准则。根据文献［14］，冰浆流体管道流动临界雷诺数的推荐值为Rec'=3 000。本文亦是参照此判别准则来划分浆体所处的流态区域的。

2.3 结果分析

在冰浆的管道输送中，冰粒子与载流体间的密度差异使得冰浆呈现出不同程度的非均质性流动特征。图3给出了基于两相流欧拉-欧拉模型［15］数值解算出的不同运行工况下冰浆流动过程中冰粒子的浓度分布。由图3易知，随着流动速度的增加，冰粒子沿着管道截面趋于均布。此时，可借助于拟单相流方法来研究冰浆的流变特性及流动阻力。

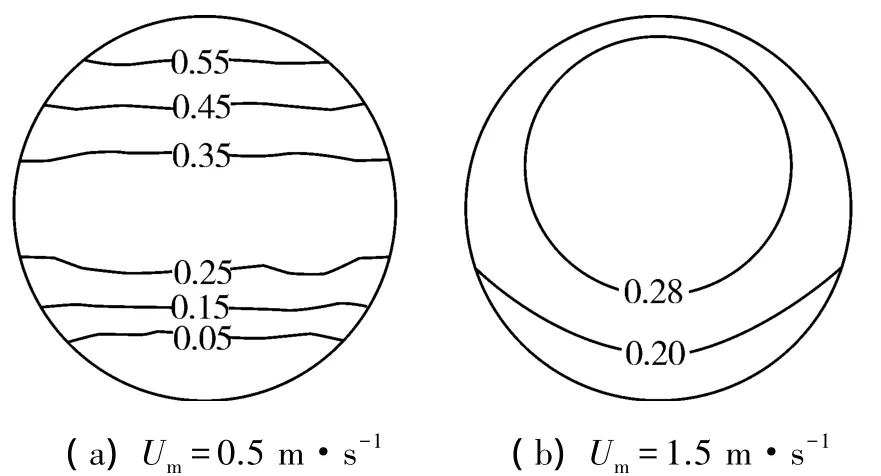
图3 冰浆输送过程中冰粒子浓度分布(DN 25/IPF=25%)Fig.3 Ice particle distribution during ice slurry flow(DN 25/IPF=25%)

图4给出了基于拟单相流方法所得到的冰浆在不同管径内流动时，浆体的流变系数k和流变指数n随冰粒子浓度IPF的变化规律。其中，k和n是基于2.1节给出的流变模型，利用数据拟合方法，拟合出在相同冰粒子浓度、不同浆体输送速度时，管壁切应力与剪切速度间的数学关系式，进而得到每一个冰粒子浓度工况时所对应的k和n。

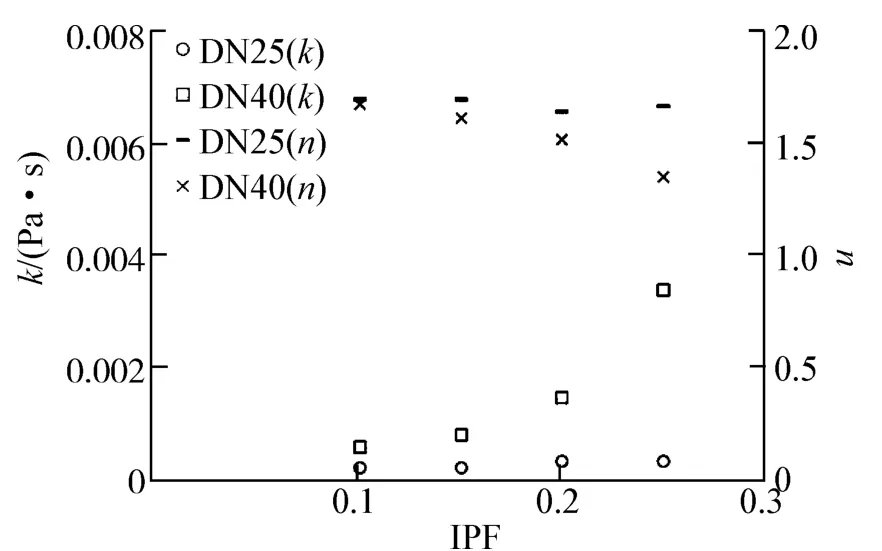
图4 冰浆流体流变参数随冰粒子浓度变化规律Fig.4 Rheological parameters versus IPF for ice slurry flow

由图4不难发现，随着冰粒子浓度及管道尺寸的增大，流变系数k逐渐增大。与此同时，流变指数n的变化规律则与流变系数k相反。但当管径减小时，流变系数k与流变指数n随冰粒子浓度的变化趋势趋于平缓。由此可见，冰浆的流变特性与冰粒子浓度及管道尺寸密切相关。而且随着冰粒子浓度及管道尺寸的增加，浆体非牛顿流变特性变得愈发显著。此外，结合图4中流变指数n的分布范围(1.34≤n≤1.69)可知，流变指数满足n＞1。因此，文中所采用的冰浆流体属于剪切稠化流体，亦即膨胀型流体。

基于冰浆管道压降实验测试结果和拟单相流管路能量损失计算方法［16］，图5给出了在 DN40和DN25的水平管道内，当冰粒子浓度不同时，管道阻力系数随平均流速的变化规律。由图5可知，在冰浆输送过程中，管道阻力系数将随着流速的减小而增大。而且随着流速的减小，冰粒子浓度变化亦会对阻力系数分布产生一定影响，即，冰浆流速越小，冰粒子浓度越高，管道的阻力系数越大，如图5(a)所示。然而当管径减小时，因浓度变化对管道阻力系数影响的差异性会随之减弱，如图5(b)。这是因为随着管径的减小，冰粒子沿管道截面分布的不均匀性减弱，进而使得管道顶部冰粒子浓度下降，冰粒子与管道壁面间相互作用随之减弱，因此削弱了浓度变化对管道阻力系数产生的影响。

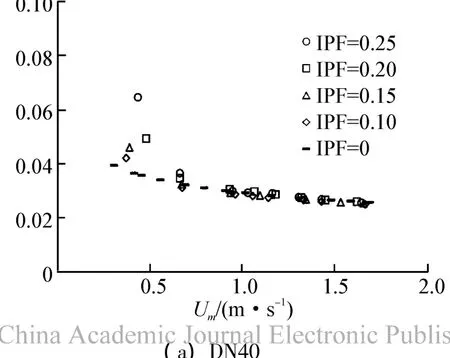
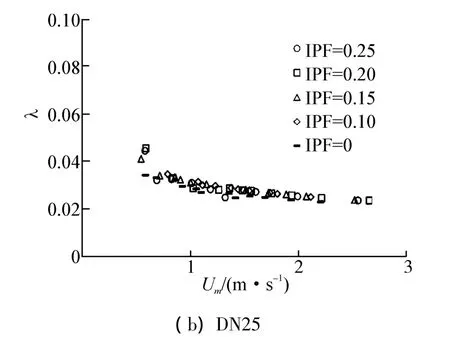
图5 水平管道内冰浆流体阻力系数随流速变化规律Fig.5 Friction factor versus U m for ice slurry flow in horizontal pipe

综上可知，冰浆流变参数及流动阻力均受到浆体流速、冰粒子浓度及输送管径的影响。因此，当流变参数发生变化时，流动阻力也会随之改变。如图4，当管道直径增大、冰粒子浓度升高时，浆体的流变系数增大、流变指数减小，此时若系统处于低速运行，则冰浆管道流动的阻力系数将呈现出显著差异性，如图5所示。例如，当浆体在DN40管道内流动时，Um分别为 0.37 m·s-1和 0.43 m·s-1，IPF 分别为10%和25%，相应的流变系数分别为0.000 6Pa·s和0.003 4Pa·s，流变指数分别为 1.667和1.344(见图4)，此时2工况所对应的阻力系数差异可达34.8%(见图5)。结合图3中冰粒子的浓度分布不难发现，当冰浆处于低速、高浓度工况下流动时，管道顶部冰粒子浓度急剧升高。此时，冰粒子与管道壁面间的相互作用增强，冰浆流体表现出明显的非牛顿流变特性。因此，当冰浆流体的平均浓度升高时，其流动阻力系数与低浓度浆体的流动阻力系数相比产生了较大的偏差。

基于2.1、2.2节所介绍的冰浆幂律流变模型和管道压降计算方法［14］，图6给出了冰浆流动管道压降的预测值与实验值对比。

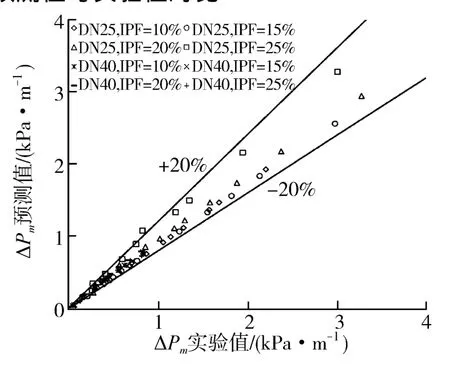
图6 冰浆流动管道压降的预测值与实验值对比Fig.6 Comparison between predicted and measured pressure d rop for ice slurry flow

由对比结果可知，预测值与实验值间取得了较好的一致性，其相对误差可控制在±20%内。

4 结论

本文采用实验测试与非牛顿流变理论相结合的方法，研究了在不同运行工况下，长距离输送管线内冰浆流体等温流动的流变特性和阻力特性。主要结论如下:

1)本研究所采用的冰浆隶属于剪切稠化流体，浆体的流变特性满足幂律流变特征，其流变参数与冰粒子的浓度及管道直径密切相关。其中，流变系数将随着冰粒子浓度及管径的增大而增大，而流变指数的变化规律则与流变系数相反。

2)流变参数的改变直接影响冰浆流动阻力特性的分布。当流速较低时，随着流变系数的增大及流变指数的减小，冰浆流体管道流动的阻力系数呈现出显著差异性，最大差异可达34.8%。

3)基于幂律流变特征，预测了水平管道内冰浆流动的管道压降。与实测结果对比发现，预测误差可控制在±20%内。

［1］EGOLF PW，KAUFFELD M.From physical properties of ice slurries to industrial ice slurry applications［J］.International Journal of Refrigeration，2005，28(1):1-12.

［2］ILLAN F，VIEDMA A.Heat exchanger performance modeling using ice slurry as secondary refrigerant［J］.International Journal of Refrigeration，2012，35(5):1275-1283.

［3］姚豪，周春艳，梁德清，等.水合物浆和冰浆高密度潜热输送研究进展［J］.化工学报，2003，54(S1):57-61.YAO Hao，ZHOU Chunyan，LIANG Deqing，et al.Recent research advances on hydrate slurry and ice slurry for high density latent-heat transportation［J］.Journal of Chemical Industry and Engineering(China)，2003，54(S1):57-61.

［4］GROZDEK M，KHODABANDEH R，LUNDQVIST P.Experimental investigation of ice slurry flow pressure drop in horizontal tubes［J］.Experimental Thermal and Fluid Science，2009，33(2):357-370.

［5］ILLAN F，VIEDMA A.Experimental study on pressure drop and heat transfer in pipelines for brine based ice slurry part II:dimensional analysis and rheological model［J］.International Journal of Refrigeration，2009，32(5):1024-1031.

［6］AYEL V，LOTTIN O，PEERHOSSAINIH.Rheology，flow behaviour and heat transfer of ice slurries:a review of the state of the art［J］.International Journal of Refrigeration，2003，26(1):95-107.

［7］KITANOVSKIA，VUARNOZ D，CAESAR D A，et al.The fluid dynamics of ice slurry［J］.International Journal of Refrigeration，2005，28(1):37-50.

［8］KAUFFELD M，KAWAJIM，EGOLF PW.Handbook on ice slurries，fundamentals and engineering［M］.Paris:International Institute of Refrigeration，2005:120-121.

［9］KAUSHAL D R，SATO K，TOYOTA T，et al.Effect of particle size distribution on pressure drop and concentration pr of ile in pipeline flow of highly concentrated slurry［J］.International Journal of Multiphase Flow，2005，31(7):809-823.

［10］BEDECARRATS J P，STRUB F，PEUVREL C.Thermal and hydrodynamic considerations of ice slurry in heat exchangers［J］.International Journal of Refrigeration，2009，32(7):1794-1800.

［11］沈仲棠，刘鹤年.非牛顿流体力学及其应用［M］.北京:高等教育出版社，1989:63-72.

［12］CHHABRA R P，RICHARDSON JF.Non-Newtonian flow in the process industries［M］.Oxford:Butter worth-Heinemann，1999:74-78.

［13］MELLARIS，BOUMAZA M，EGOLF PW.Physicalmodeling，numerical simulations and experimental investigations of non-Newtonian ice slurry flows［J］.International Journal of Refrigeration，2012，35(5):1284-1291.

［14］NIEZGODA-ZELASKO B，ZALEWSKI W.Momentum transfer of ice slurry flows in tubes，experimental investigations［J］.International Journal of Refrigeration，2006，29(3):418-428.

［15］WANG JH，WANG SG，ZHANG T F，et al.Numerical investigation of ice slurry isothermal flow in various pipes［J］.International Journal of Refrigeration，2013，36(1):70-80.

［16］蔡增基，龙天渝.流体力学泵与风机［M］.北京:中国建筑工业出版社，1999:90-91.CAIZ J，LONG T Y.Hydrodynamics of pumps and fans［M］.Beijing:China Architecture and Building Press，1999:90-91.