基于逐步等效平面法的可靠性敏度分析方法

王杰方，安伟光，宋向华

(哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001)

结构设计过程中，结构可靠性并不是唯一的度量标准，分析关于结构性能参数的可靠性敏度也是十分重要的［1］。可靠性敏度分析是一种定量的确定基本变量分布参数的变化对结构失效概率的影响程度的方法，它能够为鉴别最重要的设计参数提供重要的信息。

目前，对可靠性敏度方法的分析和研究十分广泛［2-4］，主要有3类:1)针对线性或非线性程度不高的极限状态方程，采用基于改进的一次二阶矩(the advanced first order and second moment method，AFOSM)和概率网格评估方法(probabilistic network evaluation technique，PNET)相结合的近似解析法［5-6］(AFOSM-PNET法);2)针对隐式极限状态方程，采用基于Monte-Carlo法［7］和基于自适应重要抽样的数值模拟法［8］;3)利用随机响应面法［9］将隐式的结构响应函数转换成显式函数，并在显式响应函数基础上采用第1类方法进行敏度分析。第1类方法计算工作量较小，但不适合非线性程度高的极限状态方程;第2类方法适用于任何情况的极限状态方程，但对于小失效概率情况下的大型复杂结构的敏度分析，这类方法的计算效率很低。另外，文献［10］中还介绍了基于线抽样的可靠性敏度分析方法。

为了解决复杂结构系统的敏度分析问题，本文提出了基于有限步长迭代法(limit step length iteration method，LSLIM)和逐步等效平面法(step-bystep equivalent plane method，SSEPM)的可靠性敏度分析方法——LSLIM-SSEPM法。

1 系统失效概率的敏度表达式

1.1 等效可靠性指标

假设系统的基本随机变量服从正态分布(若不服从正态分布，可以转化为正态分布)，经有限步长迭代法处理后，将非线性的安全余量转化为用标准正态随机变量表示的线性等效功能函数:

式中:yj( j=1，2，…，n)是服从标准正态分布的基本 随 机 变 量， Bi= (Bi1，Bi2，…，Bin)(i=1，2，…，m )为单位向量，第i个等效功能函数的常数项βi为其等效可靠性指标。

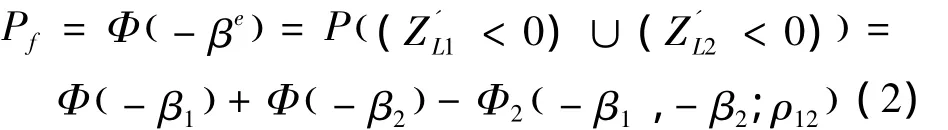
式中:ρ12为2个失效模式的相关系数，βe为该串联体系的等效可靠性指标。

1.2 系统失效概率的敏度表达式

由式(2)有，2个失效模式的串联系统失效概率对基本随机变量xi的均值μxi的一阶敏度为

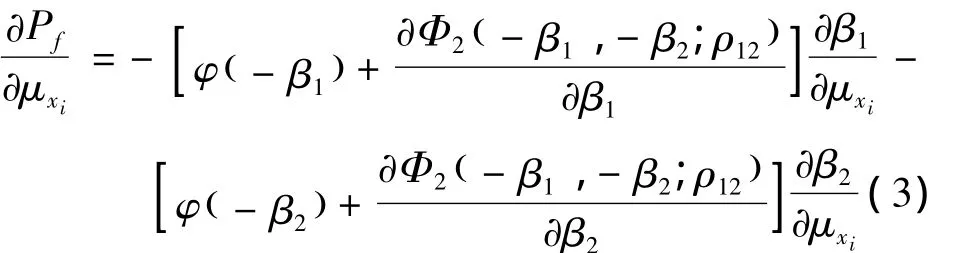
式中:φ()·为标准正态分布的密度函数。将上式中的μxi换成σxi即为系统失效概率对基本随机变量xi的标准差σxi的一阶敏度。

由二维标准正态分布得

1.3 安全余量中含综合随机变量的敏度分析

将综合随机变量zj表示为基本随机变量的函数

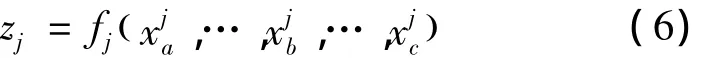
式中:zj为安全余量中第j个综合随机变量，中下标a、b、c表示zj中所含的基本随机变量在所有的基本随机变量中的位置编号，中的上标j表示基本随机变量xa出现在第j个综合随机变量zj中。

假设某个基本随机变量xa只出现在综合随机变量中，根据复合求导法则，系统失效概率对基本随机变量xa的均值μxa的一阶敏度为

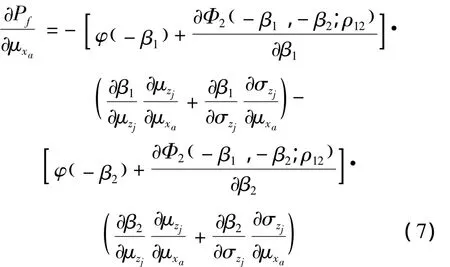
将上式中的μxa换成σxa即为系统失效概率对基本随机变量xi的标准差σxa的一阶敏度。

1.4 多失效模式串联系统的可靠性敏度分析

多失效模式(m＞2)串联系统的可靠性敏度分析步骤为:

式中:串联系统的等效可靠指标βe1公式为

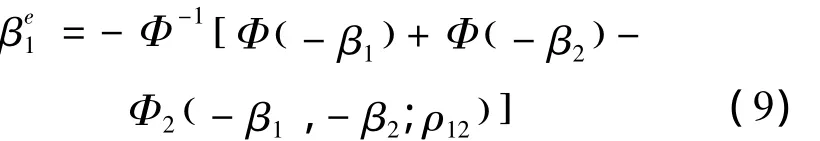
3)由式(3)及最后一次等效所得的参数可得多失效模式系统失效概率对基本变量xi的均值的偏导数。

2 单个失效模式可靠性指标敏度表达式

从上节可知，只要确定 ∂β1/∂μxi、∂β2/∂μxi、∂β1/∂σxi、∂β2/∂σxi，即可求得系统失效概率的敏度表达式。将非线性的失效模式功能函数线性化是求解单个失效模式可靠性指标的敏度表达式的前提，本文给出的LSLIM-SSEPM法采用有限步长迭代法来处理这一线性化的过程，其优点是收敛速度快、迭代精度高，对于非线性程度较高的结构功能函数也是适用的。

2.1 功能函数线性化

对于结构功能函数非线性程度较高的情况，用改进的一次二阶矩法计算可能会出现迭代不收敛，为了解决求解可靠性指标迭代不收敛的情况，采用可调节步长的有限步长迭代法，依据有限步长迭代法有

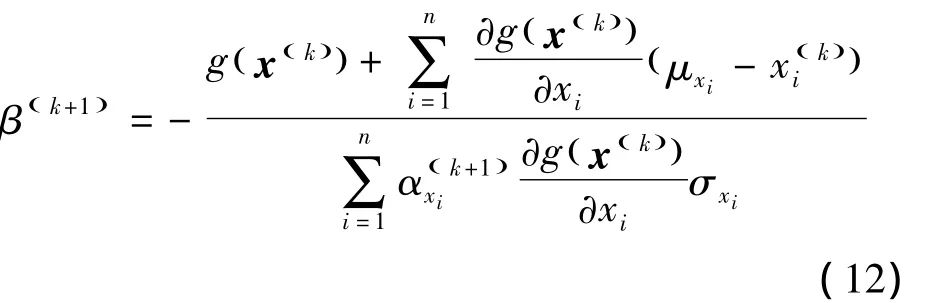
采用式(11)～(13)获得收敛的迭代验算点x*，那么，在迭代验算点处进行泰勒展开，获得式(1)中标准正态空间下的线性化等效功能函数为

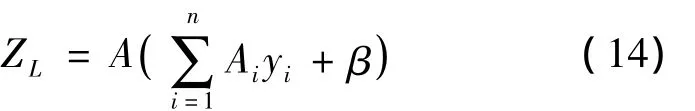
式中:

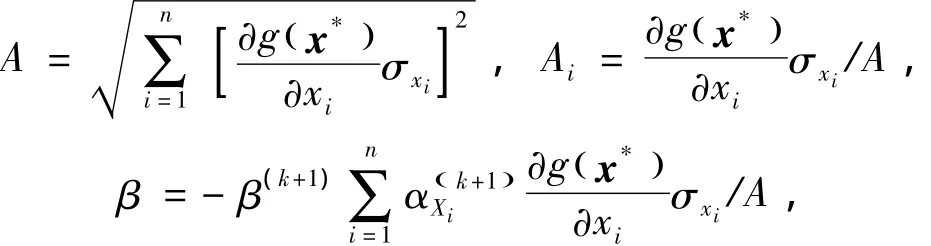
yi为标准正态空间中的基本随机变量。

2.2 单个失效模式可靠性指标的敏度表达式

对于任意形式的安全余量，其单个失效模式的可靠性指标对基本变量均值的敏度表达式可以表示为［5］

由于μxi=σxi/νi，所以单个失效模式的可靠性指标对基本变量标准差的敏度表达式为

由式(15)中可知，基本随机变量服从标准正态分布时，变异系数 νi( i=1，2，…，4 )为无穷大，因此式(15)的分子中第2项的值为0，则式(15)可简化为

采用等效步长迭代法分析系统敏度时，由于线性化的等效功能函数中的基本随机变量为相互独立的标准正态分布函数，因此单个失效模式对基本随机变量均值的敏度可以表示为式(17)所示的最简化的表达式。

3 LSLIM-SSEPM方法验证

3.1 算例1

验证逐步等效平面法计算失效概率的有效性，并给出改进计算精度的方法。设4个线性化的安全余量为［11］

假设上述6个基本随机变量均服从标准正态随机分布且相互独立。算例可靠性指标很高，因此在采用Monte-Carlo法计算失效概率时，需要很高的打点次数才能满足计算精度的要求。本文的打点次数为1 000 000组，由于Monte-Carlo法得到的失效概率具有一定的随机性，为保证结果的精确性，经过60次计算，得到趋于稳定的系统失效概率平均值为μPf=4.929 8 ×10-4。

经试算发现，逐步等效平面法的计算结果与等效路径有关，将算例1中的4个安全余量按不同的等效路径进行逐步等效，所得的计算结果如表1所示，表1的最后一列给出了逐步等效平面法的计算结果与Monte-Carlo法的计算结果μPf=4.929 8×10-4的误差。

表1 算例1的失效概率Table 1 The failure probability of example 1

从表1可知:

1)对比第1、3、5三组数据可知，将可靠性指标最低的安全余量(M3)在等效路径中安排得越靠前，计算精度越低;对比第7、9、11三组数据可知，将可靠性指标最高的安全余量(M2)在等效路径中安排得越靠前，计算精度越高。

2)对比第1(按可靠性指标从高到低排列)和7(按可靠性指标从低到高排列)两组数据可知，若等效路径按可靠性指标从高到低排序，计算误差(1.01%)小于按可靠性指标从低到高的排序的误差(11.36%)。

因此，在利用逐步等效平面法计算系统失效概率的过程中，按可靠性指标由高到低来安排等效路径是提高计算精度的有效方法。在后续算例中进行可靠性敏度分析时也将利用这一结论。

3.2 算例2

设4个线性安全余量分别为

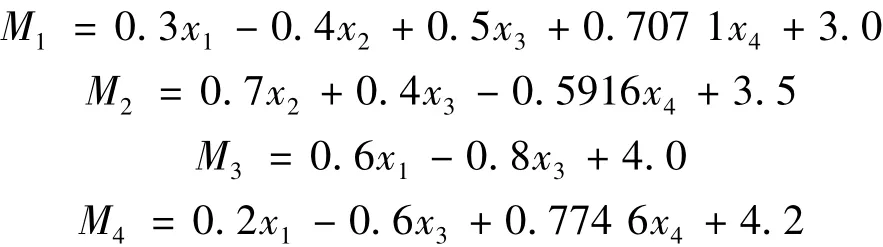
求4个安全余量组成的串联系统失效概率对基本随机变量均值的敏度。x1、x2、x3、x4为不相关的标准正态随机变量。分别采用文献［7］中基于Monte-Carlo的方法、文献［5］中的AFOSM-PNET方法以及本文的LSLIM-SSEPM所得计算结果见表2。表2中给出了由以上3种方法获得的系统失效概率Pf、系统失效概率对基本变量均值的敏度∂Pf/∂μxi以及运算时间t。

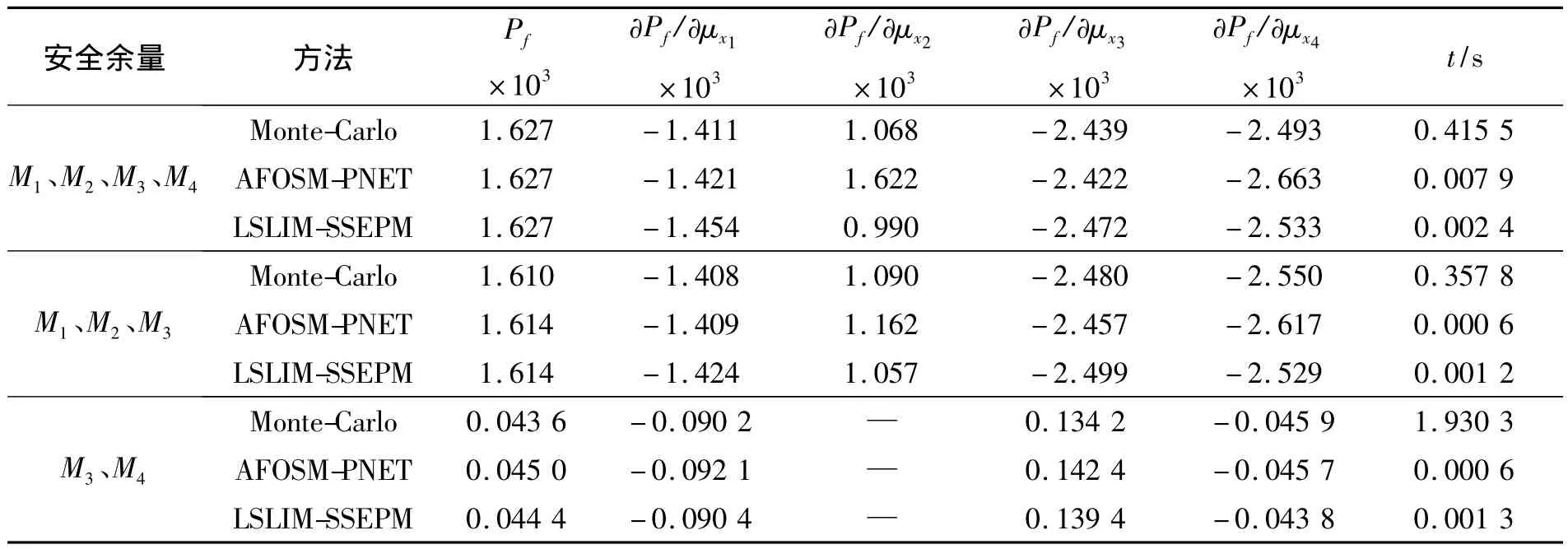
表2 算例2的计算结果Table 2 The results of examp le 2

从表2中可以得出以下结论:

1)采用以上3种方法所得的计算结果能基本保持一致，这也说明了本文给出的LSLIM-SSEPM法用于分析具有线性安全余量系统可靠性敏度的可行性。

2)运算时间方面，基于Monte-Carlo法的敏度分析方法是最耗时的，AFOSM-PNET法和LSLIM-SSEPM法的计算量都比Monte-Carlo法要小得多，这也说明了本文给出的LSLIM-SSEPM法的高效性。

因此，在进行具有线性安全余量的系统可靠性敏度分析时，LSLIM-SSEPM法是可行且高效的。

采用LSLIM-SSEPM法对算例2进行敏度分析，并在表3中给出了不同的等效路径对应的计算结果。以基于Monte-Carlo法的敏度分析方法的计算结果为基准，从表3中可以得到以下结论:

1)不同的等效路径下，系统失效概率对基本随机变量敏度的计算结果差别较大，例如，将表3中的第1组数和第7组数相比，敏度值的偏差达到20%以上，这说明采用LSLIM-SSEPM法分析系统可靠性敏度时，选择正确的等效路径是十分重要的。

2)等效路径取表3的1～3组，采用LSLIM-SSEPM法所得的敏度结果与基于Monte-Carlo法的敏度分析方法获得的结果差别较大，这3种等效路径的共同点是:可靠性指标高的安全余量(M4)在等效路径中被安排的较靠后;等效路径取表3中的4～7组时，采用LSLIM-SSEPM法所得的敏度结果与基于Monte-Carlo法的敏度分析方法获得的结果相比，误差相对较小，这4种等效路径的共同点是:可靠性指标低的安全余量(M1)在等效路径中被安排得较靠后。

因此，将可靠性指标越高的安全余量安排在等效路径的前面，且将可靠性指标越低的安全余量安排在等效路径的后面，LSLIM-SSEPM法的计算结果越可靠。

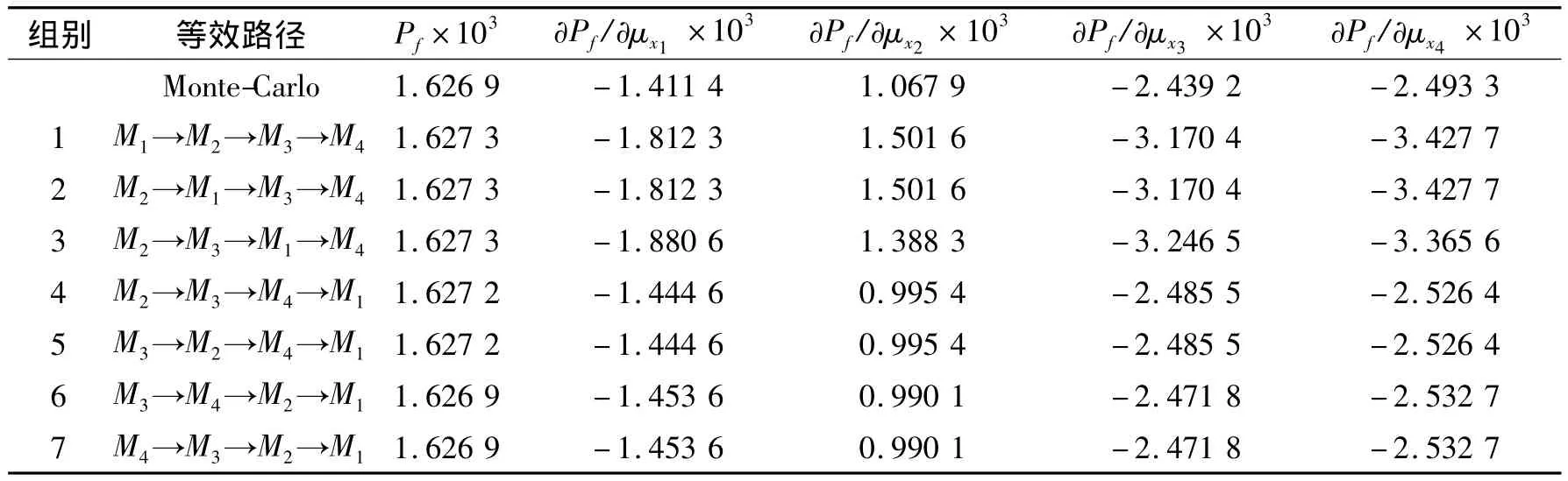
表3 不同的等效路径时算例2的计算结果Table 3 The results of exam p le 2 at different equivalent paths

3.3 算例3

假设2个串联的安全余量表达式如下

式中:随机变量R1～R5以及P的概率分布类型和统计参数见表4。

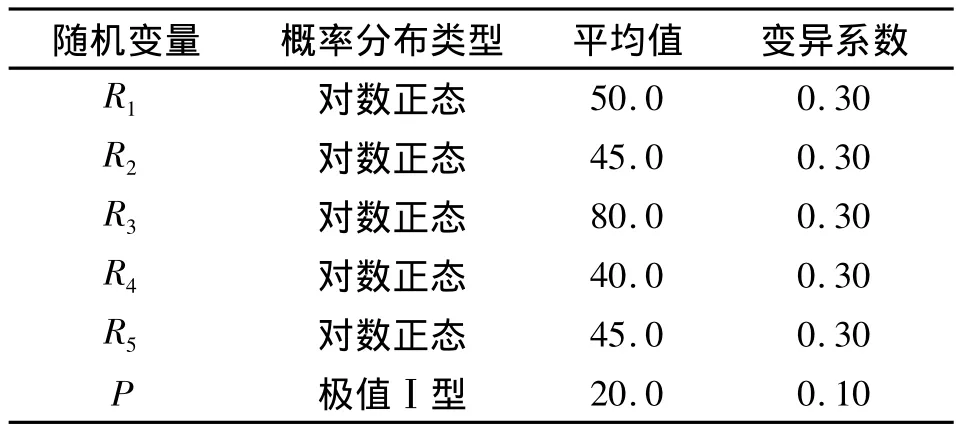
表4 随机变量的概率分布类型和统计参数Table 4 The probabilistic distribution type and statistic parameters of random variables

按照等概率原则，用标准正态随机变量表示2个非线性功能函数为

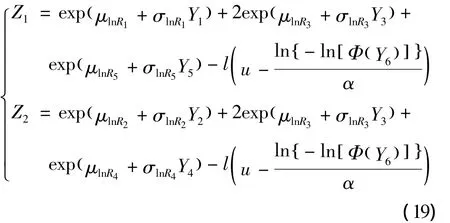
将上述2个功能函数线性化为

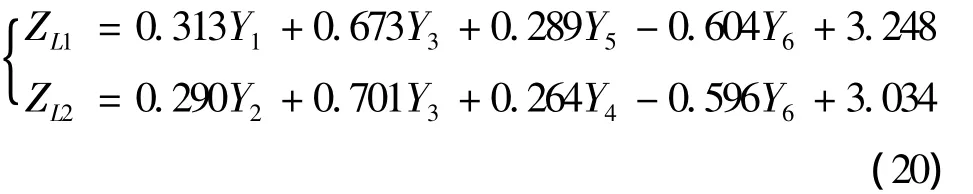
表5中分别给出了采用Monte-Carlo法计算的式(19)的2个非线性和式(20)的2个线性化后的功能函数的可靠性指标以及系统可靠性指标。

由表5可知，采用本文式(11)～(14)的方法对算例3中的2个非线性的安全余量进行线性化后所得的可靠性指标值与非线性的安全余量的可靠性指标值的结果相近，这说明采用本文的方法对非线性的安全余量进行线性化是可行的。

表5 算例3的可靠性指标Table 5 The reliability index of examp le 3

分别采用文献［7］中基于Monte-Carlo的方法、文献［5］中的方法(AFOSM-PNET法)以及LSLIMSSEPM法对算例3进行敏度分析。为了保证计算结果的稳定性，在基于Monte-Carlo法的敏度分析方法中，基本随机变量的打点次数为10 000 000组。表6中给出了由以上3种方法获得的系统失效概率Pf、系统失效概率对基本变量均值的敏度∂Pf/∂μyi以及运算时间t。

从表6中可知:

1)采用以上3种方法所得的计算结果能基本保持一致。且Monte-Carlo法和本文的LSLIM-SSEPM法结果更为接近，这也说明了本文的LSLIM-SSEPM法用于分析具有非线性安全余量系统可靠性敏度的可行性，且LSLIM-SSEPM法比基于Monte-Carlo法的敏度分析方法更高效，比AFOSM-PNET法的计算结果更精确。

2)就运算时间而言，为了保证基于Monte-Carlo法的敏度分析方法的计算精度，必须保证基本随机变量的打点数，从表6中可以看出这种方法是最耗时的，对比AFOSM-PNET法和LSLIM-SSEPM法，其运算时间都很短，这也说明了本文给出的LSLIMSSEPM法的高效性。

因此，在进行具有非线性安全余量的系统可靠性敏度分析时，LSLIM-SSEPM法是可行且高效的。

表6 算例3的计算结果Table 6 The results of examp le 3

4 结论

本文提出了一种可靠性灵敏度分析方法——LSLIM-SSEPM法，并给出了改进该方法计算精度的措施。从算例中可得出如下结论:

1)在计算系统失效概率时，按可靠性指标由高到低来安排等效路径是提高计算精度的有效方法;

2)LSLIM-SSEPM法和基于Monte-Carlo的敏度分析方法计算结果相近，但LSLIM-SSEPM法比基于Monte-Carlo的敏度分析方法效率高;在LSLIM-SSEPM法和AFOSM-PNET法计算量都很小的情况下，LSLIMSSEPM法的计算结果比AFOSM-PNET法更精确;

3)在多失效模式的系统中，将可靠性指标越高的安全余量安排在等效路径的前面，且将可靠性指标越低的安全余量安排在等效路径的后面，LSLIMSSEPM法的计算结果越可靠。

LSLIM-SSEPM法具有通用性，可用MATLAB编写通用的计算程序，具有一定的工程实用价值。

［1］VALDEBENITOM A，JENSENH A，SCHUELLERG I，et al.Reliability sensitivity estimation of linear systems under stochastic excitation［J］.Computers and Structures，2012，92-93:257-268.

［2］宋军，吕震宙.非正态变量可靠性灵敏度分析方法［J］.机械强度，2008，30(1):52-57.SONG Jun，LU Zhenzhou.Reliability sensitivity method for non-normal variable ［J］.Journal of Mechanical Strength，2008，30(1):52-57

［3］杨周.非正态分布参数的机械构件的可靠性灵敏度与可靠性稳健设计［D］.沈阳:东北大学，2010:23-26.YANG Zhou.Reliability-based sensitivity and reliability-based robust design for mechanical components with non-normal random variables［D］.Shenyang:Journal of Mechanical Strength，2010:23-26.

［4］杨杰，张崎，黄一.结构可靠性灵敏度因子的一种新指标［J］.工程力学，2013，30(6):16-21.YANG Jie，ZHANG Qi，HUANG Yi.A new sensitivity factor for structural reliability［J］.Engineering Mechanics，2013，30(6):16-21.

［5］赵维涛，张大千，于秀坤，等.空间梁板结构可靠性优化的全局最优解［J］.上海航天，2007，5:1-4.ZHAOWeitao，ZHANG Daqian，YU Xiukun，et al.Global optimal solution of space beam-plate structural reliability optimization ［J］.Aerospace Shanghai，2007，5:1-4.

［6］安伟光，孙克淋，陈卫东，等.随机结构系统基于可靠性的优化设计［J］.应用数学和力学，2005，26(10):1175-1182.ANWeiguang，SUN Kelin，CHEN Weidong，et al.Optimum design based on reliability in stochastic structure systems［J］.Applied Mathenmatics and Mechanics，2005，26(10):1175-1182.

［7］赵维涛，张旭.基于Monte-Carlo方法的结构系统可靠度计算及敏度分析［J］.计算力学学报，2011，28(2):200-204.ZHAOWeitao，ZHANGXu.Reliability calculation and reliability sensitivity analysis of structural system based on Monte-Carlo method ［J］.Chinese Journal of Computational Mechanics，2011，28(2):200-204.

［8］康春华.基于自适应重要抽样的可靠性灵敏度分析方法［J］.机械强度，2007，29(6):946-951.KANG Chunhua.Reliability sensitivity analysis based on adaptive importance samplingmethod［J］.Journal of Mechanical Strength，2007，29(6):946-951.

［9］乔红威，吕震宙，赵新攀.基于随机响应面法的可靠性灵敏度分析及可靠性优化设计［J］.计算力学学报，2010，27(2):207-212.QIAO Hongwei，LYU Zhenzhou，ZHAO Xinpan.Reliability sensitivity analysis and reliability-based design optimization based on stochastic response surfaces method ［J］.Chinese Journal of Computational Mechanics，2010，27(2):207-212.

［10］LYU Zhenzhou，SONG Shufang，YUE Zhufeng，et al.Reliability sensitivitymethod by line sampling［J］.Structural Safety，2008(30):517-532

［11］贡金鑫.工程结构可靠度计算方法［M］.大连:大连理工大学出版社，2003:256-268.GONG Jinxin.Computationalmethods for realiability of engineering structures［M］.Dalian:Dalian University of Technology Press，2003:256-268.