基于演化博弈的审计合谋机制分析*

蔡创

(北京物资学院，北京市 101149)

一 引言

审计委托人与被审计对象之间存在委托代理关系，并具有不同的利益诉求，审计委托人要求被审计对象认真履行契约，并真实反映其财务报表等各类经济数据。由于存在信息不对称，被审计对象可能会利用信息优势为自身谋取最大化利益，并因此而损害审计委托人的利益。因此审计委托人不得不委托外部审计机构对被审计对象加以监督，那意味着审计委托人必须以放弃一部分利益为代价(监督成本)才能获得被审计对象掌握的不对称信息，但问题是，外部审计机构同样是盈利机构，一样追逐利益最大化，被审计对象对其逆向贿赂会影响其独立性。外部审计机构是否严格遵守约定对被审计对象进行监督，则取决于其在监督与合谋两种策略下的得益大小。同时，审计合谋行为大大增加了审计委托人的监督成本，给经济活动带来了低效。对审计合谋的研究，已有不少文献。雷光勇(2004)[1]从审计合谋的共生机制出发，在内在机理和外在环境两个方面对审计合谋进行考察，研究审计委托人与被审计对象的合谋关系，利用静态博弈寻找纳什均衡解，提出审计合谋是注册会计师提供“购买意见”诱因与被审计对象“寻租”诱因耦合与互动的结果。类似的研究还有刘国常和韩春生(2005)[2]、贡峻(2004)[3]、龚启辉和刘桂良(2006)[4]等。此外，余玉苗，田娟，朱业明(2007)[5]等人则对双重审计制度下的两个注册会计师与被审计对象间的合谋情形作出了分析，着重考察了注册会计师甲和乙之间的博弈关系，得出双重审计制度在外部监督力度强化和适当激励机制建立的条件下有利于降低对审计师的监督成本。对于审计合谋行为随着时间的演变趋势与规律则鲜有文献涉及，故本文从动态角度出发，依据演化博弈理论，建立了一个包含审计委托人群体、被审计对象群体和外部审计机构群体的动态博弈模型。该模型的优点在于既考量到三者间的博弈关系，亦将每一方群体内部之间的博弈考虑在内，另外引入了时间因素。

二 演化博弈模型的建立与分析

(一)假设

假设1 博弈者(player)总是选择具有更高收益的那个策略。这一假设是基于人的逐利性。

假设2 博弈中的三者，审计委托人、被审计对象和外部审计机构各自可选的策略构成一个2x2x2的策略集(策略矩阵)，如下所示:

审计委托人(委托，不委托)

被审计对象(舞弊，不舞弊)

外部审计机构(监督，合谋)

假设3 在初始时刻，审计委托人中选择委托策略的比例为x，不委托比例为1－x，外部审计机构中选择监督的比例为y，合谋比例为1－y，被审计对象中选择舞弊者比例为z，不舞弊者比例为1－z，并且随着时间的推移，选择不同策略的优劣情况将变得“众所周知”，从而影响作出另一策略的博弈者的再决策，因而比例值x、y、z是随着时间动态变化的。这一假设基于社会人群具有学习性，更有利的策略将在群体中扩散开来。

假设4 本模型建立在完全市场的经济环境基础上，并不考虑非经济因素的影响，如政策规定等扭曲市场行为的因素。

(二)初步分析

下面分别对三者的博弈情况进行初步分析。

1、审计委托人。

审计委托人之所以选择委托外部审计机构对被审计对象进行监督是由于信息不对称，而该信息的获得是有成本的，该成本形成外部审计机构的收益的全部或一部分，成本大小与所委托外部审计机构的声誉品牌、被审计对象作弊的可能性大小、外部审计机构选择与被审计对象合谋的可能性大小等因素有关。当审计委托人采取委托策略时，显然被审计对象的舞弊比例z越高，外部审计机构选择合谋的比例1－y越高，那么监督成本越大，收益(pay off)越小。假设委托费用为E，我们定义当z=1，y=0即被审计对象都舞弊，外部审计机构都合谋时，审计委托人的收益为－E，写成表达式为S=K[1－z(1－y)]－E，其中K为常数，是审计委托人不采取委托策略时潜在的最大损失，反过来说损失为0即为收益最大。当审计委托人采取不委托策略时，其收益仅取决于被审计对象的舞弊比例z，有表达式S=K(1－z)。

2、被审计对象。

若没有来自外部审计机构的监督，被审计对象总是天然地要追求自身利益的最大化，若是选择舞弊策略不需要付出代价，那么其必然要选择舞弊。然而被审计对象一旦被发现舞弊，付出的代价也往往是惨重的，因此，在作出究竟是舞弊还是不舞弊的决策时，被审计对象必须仔细地权衡利弊。当被审计对象选择不舞弊时，无论审计委托人选择委托与否，其收益都是正常收益R。当被审计对象选择舞弊同时审计委托人选择不委托时，其将获得最大收益，这包括了正常收益R和审计委托人的额外损失K。当被审计对象选择舞弊同时审计委托人选择委托时，情况就较为复杂了。若外部审计机构选择监督，那么被审计对象的舞弊行为就会暴露，其不仅失去额外收益K，还要失去正常收益R，而且还有一定的处罚C，结果收益为－C(这里简化假设外部审计机构高效而正确，且对舞弊的惩罚十分严重);而外部审计机构若选择合谋，被审计对象必须付出一定代价，需要从额外收益中分出一定比例给予外部审计机构，设为v，此时被审计对象的收益为R+(1－v)K。

3、外部审计机构。

成立之初，外部审计机构的作用和目的就是为解决审计委托人与被审计对象间信息不对称的问题，同时为自己创收，但是事实往往更加复杂，外部审计机构同时掌握有来自审计委托人和被审计对象的信息，也是两者间的桥梁和枢纽，其收益原本来自于审计委托人对其支付的委托费用，但被审计对象对其贿赂影响改变了原来的“游戏规则”。通过寻租和分租，外部审计机构与被审计对象的合谋变成了可能。这可能导致审计委托人要花费更大的代价维护其潜在损失。假设委托费用为E，理论上E不应大于K，若E＞K，则审计委托人宁可采取不委托策略。在外部审计机构自身不受任何监督时，显然，接受被审计对象的合谋要求所得收益必定大于履行合约所得收益，其必然要采取合谋策略。在这里，我们给其一个概率p以使其具备一定的”东窗事发“的可能性，这种露馅给外部审计机构带来的不利将是显著的，其在审计委托人中的信誉丧失殆尽，不会再接到下一任客户的委托，从而被驱离市场。在此假设基础上，当外部审计机构采取监督策略时，无论被审计对象是否舞弊，其收益都是固定的E。当外部审计机构采取合谋策略时，默认了被审计对象采取舞弊策略的事实，若未东窗事发，则其收益为E+vK，若东窗事发，则收益为0(因为下一次博弈不再存在，此次博弈获得的收益将被稀释)。

(三)综合分析

先简化名称，审计委托人代号为A，被审计对象代号为B，外部审计机构代号为C。现在算出A、B、C采取不同策略下的得益情况。

S(A，委托)=K[1－z(1－y)]－E，S(A，不委托)=K(1－z)，

S(B，舞弊)=R(1－xy)+K(1－xy－vx+vxy)－Cxy，S(B，不舞弊)=R，

S(C，监督)=E，S(C，合谋)=(1 －p)(E+vK)，

再算出A、B、C的平均得益

S(A，均)=Kx[1－z(1－y)]－Ex+K(1－x)(1－z)=K(1－z+xyz)－Ex，

被审计对象平均收益

S(B，均)=(1－z)R+z(1－x)(R+K)－Cxyz+zx(1－y)[R+(1－v)K]，

外部审计机构平均收益

S(C，均)=yE+(1－y)p*0+(1－y)(1－p)(E+vK)=E(1－p+py)+vK(1－y－p+py)

再次指出，本文的理性经济人总是趋利避害的，同时具有自发学习性，若在某次博弈中获得的收益低于采取另一策略所获收益，那么在下一次博弈中将采取收益更高的策略。由此我们可以得出如下博弈演化方程组。

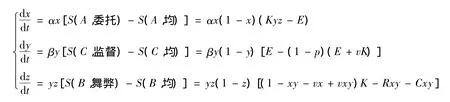
这是一个非线性变系数微分方程组，求其解析解十分困难，即使是求解数值解也比较繁杂。在这里我们并不关心x、y、z随时间的具体变化过程，而是想知道不同的参数 K、R、E、p、v、C和不同的初始状态(x0，y0，z0)对该体系最终状态有什么影响。我们可以先求其奇点，令方程组右端为0。

解得9个奇点，如下所示。

(x，y，z)=(0，0，0);(0，0，1);(1，0，0);(1，0，1);(0，1，0);(0，1，1);(1，1，0);(1，1，1);(K/(K+R+C)，1，E/K)

略去几个对本问题无意义的奇点，剩下7个奇点

(x，y，z)=(0，0，0);(0，0，1);(1，0，0);(1，0，1);(1，1，0);(1，1，1);(K/(K+R+C)，1，E/K)

现在我们要讨论这些奇点的稳定性，即在对其加以小幅度扰动后，最终结果是仍然不变，还是转换到其他演化状态。幸运的是，外部审计机构的演化方程中不含有关于x和z的信息，说明其演化方向仅由外界初始条件决定，给我们的分析带来了便利。

分析E－(1－p)(E+vK)可知，p越接近1，即合谋事发的可能性越大，则外部审计机构越倾向于监督而不是合谋，p越接近于0，即合谋事发可能性越小，外部审计机构越倾向于合谋。当p一定时，vK越大，即分租收益越大，外部审计机构越倾向于合谋，反之亦然;E越大，即委托费用越高，外部审计机构越倾向于监督，但是在p很小时，委托费用的提高带来的效果并不如意，尤其是当p=0时，无论怎样提高委托费用都无济于事了。

若外部审计机构倾向于合谋，即E－(1－p)(E+vK)＜0时，经过一定时间，选择监督策略比例必将趋于0，我们更关心系统的最终状态，将y=0带入方程组，得

由于0＜x＜1，0＜z＜1，0＜v＜1，易知 dx/dt＜0，dz/dt＞0，在t充分大时(这时y趋于0)必然成立，故(0，0，1)为系统稳定点，且知仅有该点是渐进稳定的。也就是说，一旦初始条件使得外部审计机构偏向于合谋策略，那么愿意委托审计者比例将越来越少，而被审计对象舞弊者将越来越多，“三方体系”终将崩溃，我们尤其能够看到，即使提高对外部审计机构的支付水平E还是“高薪养廉”(增加R)，或是增加对舞弊者的惩罚(提高C)，都是一种无效行为。利用matlab模拟结果如图1。当外部审计机构偏向于监督即E－(1－p)(E+vK)＞0时，经过一段时间，选择监督策略比例必将趋向于1，假设初始状态 x(0)=x0，y(0)=y0，z(0)=z0，如图2所示，

图1

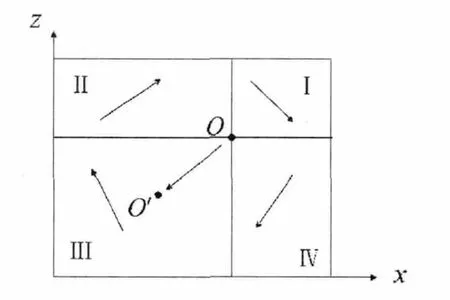
图2

点O的坐标为(K/[(K－vK+R+C)y0+vK]，E/Ky0)，点次 O 的坐标为(K/(K+R+C)，E/K)，表示随着时间的推移，y值趋于1(点O趋于点次O)的过程。经分析，在四个区域内的点(x，z)的变化趋势如图中箭头所示，即围绕着移动的点O作螺旋式运动，可知，奇点次 O(K/(K+R+C)，1，E/K)是稳定的，但是否渐进稳定，需要参照微分方程稳定性理论。对上述微分方程组进行线性方程近似处理，可写成形如

因为在E－(1－p)(E+vK)＞0时︳A︳不等于0，原方程组的奇点稳定性转化为对应线性方程组的奇点稳定性。

由特征方程︳λI－A︳=0，得

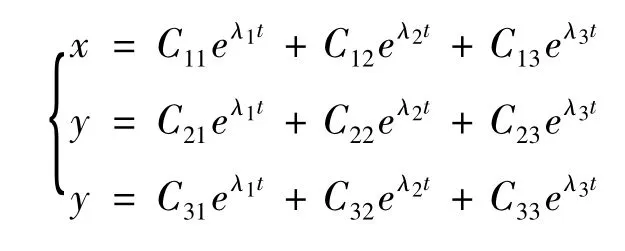
前面已假定K＞E，因此该特征方程有一个实根λ1=－β[E－(1－p)(E+vK)]，和两个纯虚根λ2，3=±sqr((αγEˆ2KR(K+R+C)(K － E)/(Kˆ2(K+R)ˆ2))i。线性方程组有形如的解。因为E－(1－p)(E+vK)＞0，故λ1＜0。实根λ1表征奇点的运动趋势，虚根λ2，3表示解的周期性，可知当t很大时点(x，y，z)螺旋地收敛于原点周围的一个极限环，故原方程组的解亦收敛于包含点次O的一个极限环(不一定是圆，但一定是封闭轨线)，这与上述分析一致。Matlab模拟结果如图3。

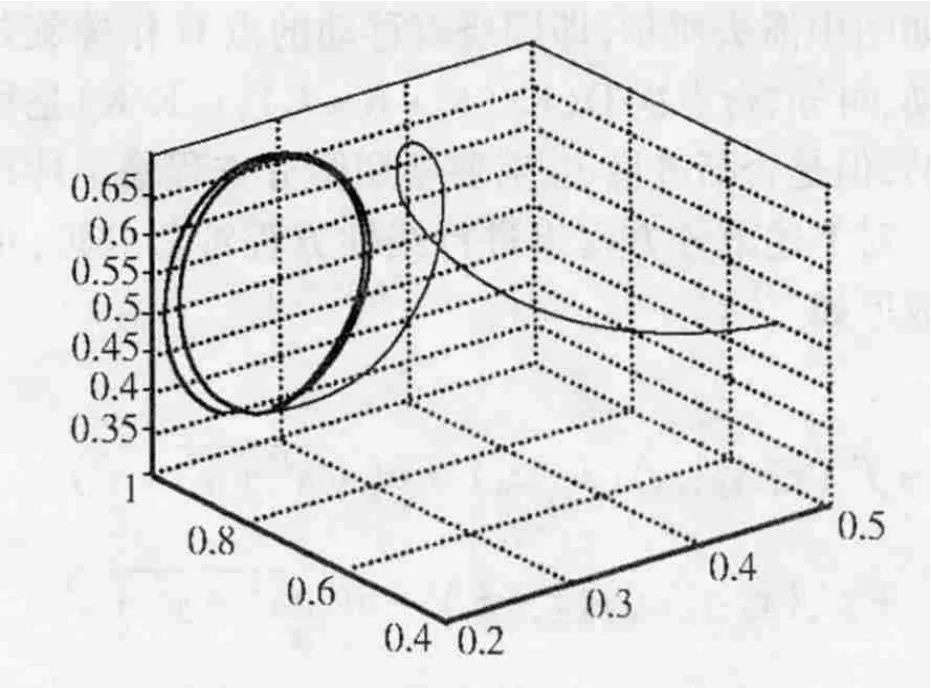
图3

对于这一结果，可以解释为.当市场逐步完善，外部审计机构普遍坚守职责后，一旦审计委托人增加，会有更多的舞弊者被发现，得到严厉的处罚，从而舞弊者大大减少，之后，审计委托人认为与对外部审计机构的支付相比，舞弊风险已经很小了，因此委托审计者减少，一旦减少到某一程度，舞弊者便又会增加，如此往复不已。这说明即使外部审计机构能够做到坚守职责，舞弊者也不会完全消失，这是消除审计委托人与被审计对象间信息不对称而必须付出的代价。

但是在现实中，政府的介入尤其是政府对企业在政策上规定了必须委托相应机构进行审计的要求，从而打断了周期性，使审计委托者委托比例维持在高位，很好的抑制了经营者的舞弊情况。此外，委托审计业务的增加也会大大降低其费用(会计事务所的市场竞争)，这是能够抑制舞弊的另一重要原因。

之所以不讨论E－(1－p)(E+vK)=0的情形，是因为在现实中，保持一个变量刚好在某个点上几乎是不可能的，通过进一步分析能容易得到，即使 E－(1－p)(E+vK)=0，也不会影响原方程的奇点性质。

三 总结

通过对“审计委托人—外部审计机构—被审计对象”三方博弈系统的分析，我们能够得到如下结论。

(1)在三方博弈系统中，外部审计机构的行为决定了系统的最终走向，当外界条件使得外部审计机构倾向于与被审计对象合谋时，系统趋于崩溃;而当外界条件促使外部审计机构严格监督被审计对象行为时，在无强制外力如政策规定等扭曲市场的行为下，则形成一个周期性的稳定系统，亦即所谓的“共生系统”。[1]

(2)抑制合谋舞弊的关键在于监督外部审计机构的行为，“监督监督者”从来都是国际上审计理论的一个重要命题，提高监督者的违规成本是一个重要手段，如“双重审计制度”就是一个可行办法。[5]这说明在审计合谋的供给方与需求方的治理中，对供给方的监督治理更为重要和关键。

在未解决“监督监督者”问题前，“高薪养廉”将是一种低效行为，甚至可能恶化合谋舞弊现象。某些文献提到抑制审计合谋靠激励与约束机制[2][3][4]，这仅在满足条件 E － (1 － p)(E+vK)＞ 0时才能够成立。

[1]雷光勇.审计合谋与财务报告舞弊:共生与治理[J].管理世界(月刊)，2004 ，(2):97－116.

[2]刘国常，韩春生.上市公司审计合谋的博弈分析和治理策略.审计与经济研究，2005，(2):31－35.

[3]贡峻.审计合谋的经济学思考[J].江苏商业会计，2004，(4):3－7.

[4]龚启辉，刘桂良.审计合谋的治理:来自审计收费模型的风险博弈分析[J].审计研究，2006，(4):68－71.

[5]余玉苗，田娟，朱业明.审计合谋的一个博弈均衡分析框架[J].管理科学学报，2007，(4):32－37.

[6]阿维纳什迪克西特，苏珊斯克丝.策略博弈(第二版)[M].北京.中国人民大学出版社，2002.