基于DMRG算法的自旋轨道耦合排斥费米气体的相变研究

韩虹，周晓凡，梁军军

（山西大学 理论物理研究所，山西 太原 030006）

0 引言

近年来，自旋轨道耦合［1］对超冷原子凝聚现象的作用引起了人们的兴趣。人们对超冷原子气体的量子特性以及凝聚态特性已经进行了大量的理论和实验研究。在文献［2］中已经在光晶格中实现了Band绝缘态和Mott绝缘态，当粒子排斥相互作用为0时，粒子数密度的分布就会在势阱中心变得非常平坦，出现了Band绝缘态；然而随着粒子间排斥相互作用的增强，发现势阱中心每个格点只占据着一个粒子，出现了Mott绝缘态。在文献［3］中，作者在超晶格中同样模拟了Band绝缘态和Mott绝缘态，发现在它们之间有一个中间体电荷密度波（BCDW）态。

本文中，我们通过密度重整化群（DMRG）研究简谐势阱下排斥相互作用的费米气体在自旋轨道耦合作用影响下的基态属性。在光晶格中，通过计算粒子数密度分布和涨落情况，分析自旋轨道耦合作用对Mott绝缘态和金属态的影响。在超晶格中，通过粒子数密度平均分布和涨落情况，分析自旋轨道耦合作用对Band绝缘态、BCDW态和Mott绝缘态的影响。

1 理论模型

一维光学晶格自旋轨道耦合（SOC）哈密顿量［4－6］

H0是存在简谐外势的一维超晶格Fermi－Hubbard模型的哈密顿量［2］，

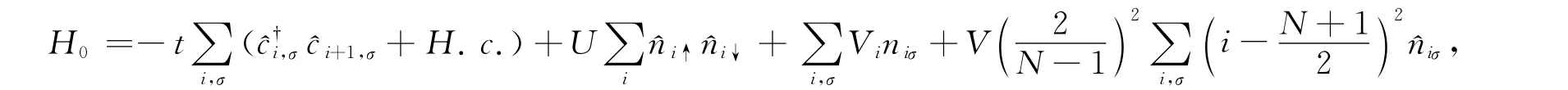
HSO是自旋轨道耦合项［1，9］

我们定义双占位周期的局域势能为V［2］i

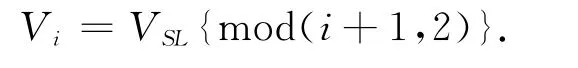
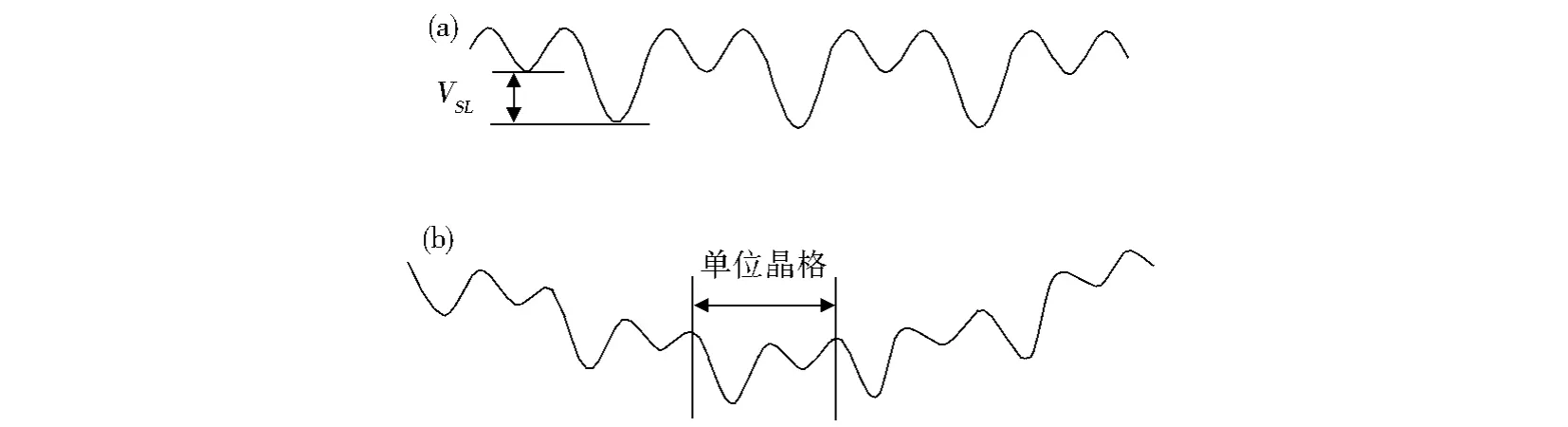
Fig.1 Potential profiles of（a）two－site periodic superlattice and（b）with a confining potential.VSLis the difference between the potential energies of odd and even sites图1 势能分布图（a）双占位周期超晶格（b）有外势的超晶格。VSL为费米子在奇偶位置的势能差

我们首先研究在晶格中的粒子数密度分布ni，而且由于超晶格的粒子数密度分布呈现复杂的锯齿状，为了便于观察，我们计算单位晶格中的平均粒子数密度分布

2 模拟结果及分析

在光晶格中，如图2（a）所示粒子数密度分布［10－12］在中间部分达到1，图2（c）所示涨落在中间部分非常小，系统处在Mott绝缘态；当自旋轨道耦合作用在处于Mott绝缘态的系统上时，从图2（b）中我们看到粒子数密度分布变为光滑曲线，图2（d）所示的涨落整体明显增大，说明自旋轨道耦合能使系统发生Mott绝缘态与金属态之间的相变。

如图2（e）所示系统在金属态下的粒子数密度分布；当自旋轨道耦合作用在处于金属态的系统上时，从图2（f）我们看到粒子数密度分布扁平，图2（h）涨落整体明显增大，说明自旋轨道耦合对系统的金属性起到增强的作用。

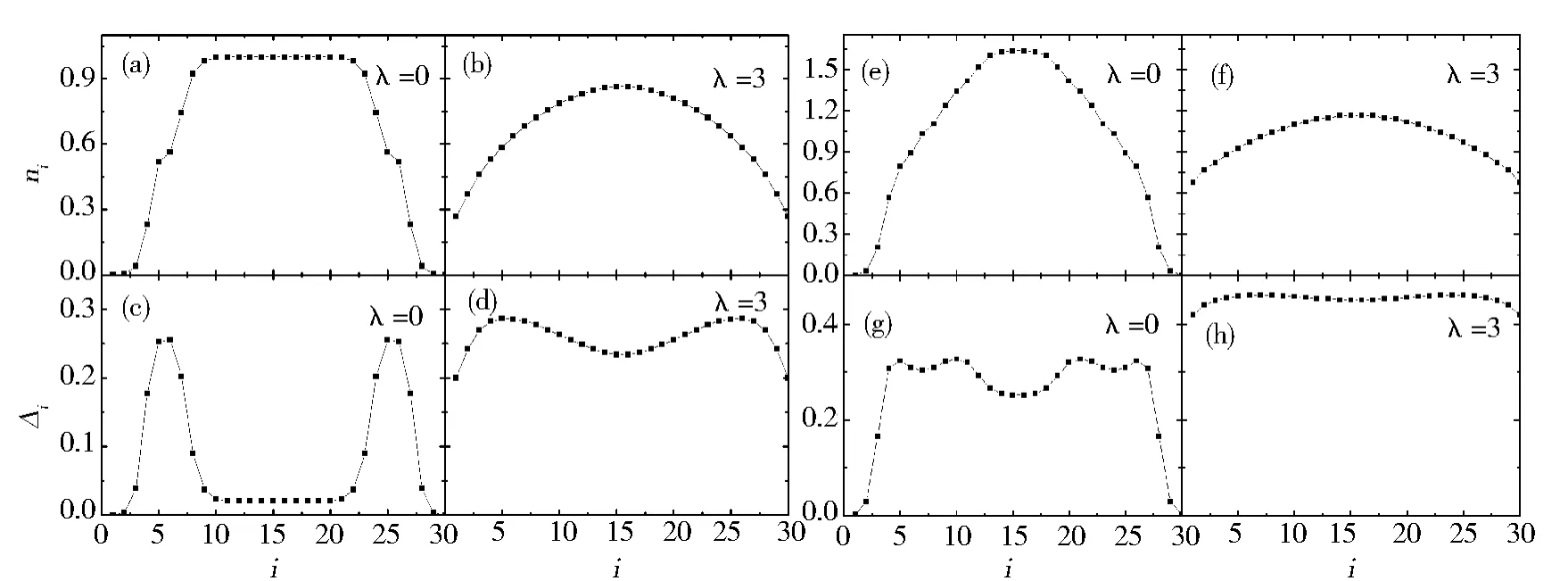
Fig.2 Density and variance of Mott insulator phase and mettallic phase with spin－orbit couplingL＝30 N＝30 V＝8 U＝3（Mott态）U＝1（金属态）图2 Mott绝缘态和金属态粒子数密度分布和涨落随着λ变化的情况

我们已经研究了在光晶格中自旋轨道耦合对费米系统的影响，现在继续探索在超晶格中产生的影响。图3所示是相互作用U＝0时，系统处于Band绝缘态的情况。从图3（a）和图3（b）中我们看到超晶格的粒子数密度分布呈复杂的锯齿状，不易观察；所以进一步观察粒子数密度平均分布，在图3（d）中，我们看到粒子数密度平均分布有所变化，但还不能确定发生相变；继续观察涨落情况，从图3（f）中看到涨落整体变大，粒子跃迁活跃，证明系统在自旋轨道耦合作用下，发生了Band绝缘态与金属态之间的相变。

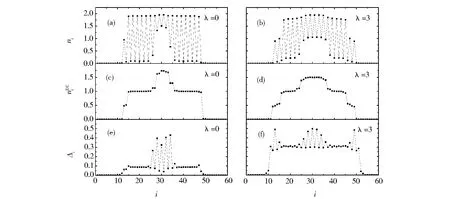
Fig.3 Density，variance，density averaged within the unit cell of Band insulator phase with spin－orbit couplingVSL＝6L＝60 N＝40 U＝0V＝20图3 Band绝缘态粒子数密度分布、涨落、单位晶格的粒子数密度平均分布随着λ变化的情况

图4是在相互作用U＝3下系统处于电荷密度波（BCDW）态［2］的情况。如图4（b）所示粒子数密度平均分布几乎平滑，系统已经相变为金属态；如图4（c）看到涨落在0.1附近，图4（d）中间的涨落大于0.1，进一步说明系统在自旋轨道耦合作用下，发生了自旋密度波（BCDW）态与金属态之间的相变。

图5是在相互作用U＝16下系统处于Mott绝缘态的情况。图5（d）所示涨落整体明显增大，说明系统在自旋轨道耦合作用下，发生Mott绝缘态与金属态之间的相变。

在超晶格中，我们已经研究了自旋轨道耦合的作用可以使系统发生相变的情况，最后通过相图进一步分析自旋轨道耦合作用由弱到强对系统的影响。图6是λ－U的相图，当自旋轨道耦合作用较弱时，系统随着相互作用强度U的增强依次出现了Band绝缘态、BCDW态、Mott绝缘态。当自旋轨道耦合作用较强时，系统仅呈现为金属态。通过相图，我们发现自旋轨道耦合可以使体系的金属性增强。

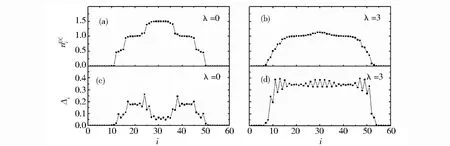
Fig.4 Density averaged within the unit cell，variance of BCDW phase with spin－orbit couplingVSL＝6L＝60 N＝40 U＝3 V＝20图4 BCDW态粒子数密度平均分布、涨落随着λ变化的情况

Fig.5 Density averaged within the unit cell，variance of Mott insulator phase with spin－orbit couplingVSL＝6L＝60 N＝40 U＝16 V＝20图5 Mott绝缘态粒子数密度平均分布、涨落随着λ变化的情况

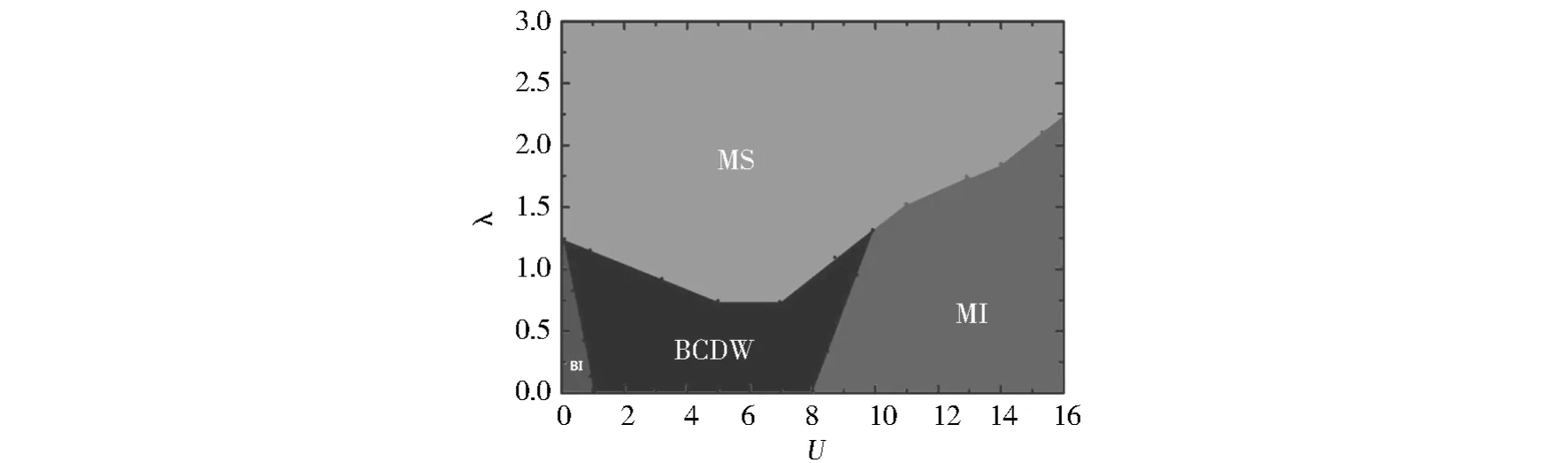
Fig.6 Phase diagram as a function of spin oribit coupledλand interraction U.Four different phases：Band insulator（BI），Bond－charge density－wave（BCDW），Mott insulator（MI），Metallic state（MS）L＝60 N＝40 V＝20图6 一维超晶格自旋轨道耦合λ和相互作用强度U的相图，其中有四种不同的相：Band绝缘态（BI）、电荷密度波态（BCDW）、Mott绝缘态（MI）、金属态（MS）

3 结论

我们用DMRG方法计算自旋轨道耦合作用下的一维光学晶格与超晶格中的排斥费米气体的相变。光晶格中，发现系统在自旋轨道耦合作用下，发生Mott绝缘态与金属态之间的相变，金属态的金属性增强；超晶格中，在不同的相互作用强度下，系统出现Band绝缘态、自旋密度波（BCDW）态和Mott绝缘态，当自旋轨道耦合作用较强时，三种态发生与金属态之间的相变。我们通过相图分析了自旋轨道耦合强度和相互作用强度对相变的影响。

［1］Qu Chun－lei，Gong Ming，Zhang Chuan－wei.FFLO or Majorana Superfluids：Quantum Phases of Fermionic Cold Atoms in Spin－orbit Coupled Optical Lattices［Z／OL］.［2013－03－14］.arXiv：1304.3926v1.

［2］Machida M，Okumura M，Yamada S，et al.Matsumoto.Mott phase in polarized two－component atomic Fermi lattice gas［J］.Phys Rev B，2008，78：235117.

［3］Takanori Yamashita，Norio Kawakami.Fermionic Atoms Trapped in a One－dimensional Optical Superlattice with Harmonic Confinement［J］.Phys Rev A，2006，74：063624.

［4］Rigol M，Muramatsu A，Batrouni G G，et al.Local Quantum Criticality in Confined Fermions on Optical Lattices［J］.Phys Rev Lett，2003，91：130403.

［5］Fabian Grusdt，Michael Hoening，Michael Fleischhauer.Topological Edge States in the one Dimensional Super－lattice Bose－Hubbard Model［Z／OL］.［2013－12－31］.arXiv：1301.7242v1.

［6］Sun Q，Zhu G B，Liu W M，et al.Spin－orbit Coupling Effects on the Superfluidity of Fermi Gas in an Optical Lattice［Z／OL］.［2013－05－19］.arXiv：1304.4511v2.

［7］李小磊，梁军军.光学晶格中一维排斥费米气体的超流特性［J］.山西大学学报：自然科学版，2013，36（2）：204－207.

［8］李小磊，梁军军.一维光学晶格中费米气体的超流特性［D］.太原：山西大学，2013.

［9］Zhou Lu，Pu Han，Zhang Wei－ping.Anderson Localization of Cold Atomic Gases with Effective Spin－orbit Interaction in a Quasiperiodic Optical Lattice［J］.Phys Rev A，2013，87：023625.

［10］Masaki Tezuka，Masahito Ueda.Density－Matrix Renormalization Group Study of Trapped Imbalanced Fermi Condensates［J］.Phys Rev Lett，2008，100：110403.

［11］Yamda S，Machida M，Ohashi Y，et al.Strong Pairing and Microscopic Inhomogeneity of Lattice Fermion Systems［J］.Physica C，2007，463：103－106.

［12］Masahiko Machida，Susumu Yamada，Yoji Ohashi，et al.Novel Pairing in the Hubbard Model with Confinement Potential［J］.Physica C，2006，445：90－93.