阴影遮蔽条件下光伏阵列的可重构优化配置方法

李锐华，闫宇星，胡波

（同济大学电子与信息工程学院，上海 201804）

光伏发电是对太阳能这种清洁能源的重要利用方式[1-3]。设计光伏发电系统时，为了获得光伏阵列的最大输出功率，需要将光伏阵列输出电压调整至最大功率点电压[4-7]。而在实际工作状态下，由于环境温度变化、光照条件变化、阴影遮蔽等因素，光伏阵列中各个光伏组件可能处于不同工作状态，从而引起单个光伏组件输出特性出现差异，使得整个光伏阵列输出特性呈现多样化、复杂化[8-11]，传统MPPT算法将无法适用，直接影响光伏发电系统效率[12-13]。为了解决这一问题，一方面只能采用更加复杂的MPPT算法以实现最大功率输出，这无疑给MPPT算法设计增加了难度；另一方面，通过优化光伏阵列结构设计以改善其输出特性，从而可以降低MPPT算法设计要求。

文献[14]通过光伏电池的典型数学模型建立光伏阵列模型，并在数学模型中体现阴影特性并对其进行计算。文献[15]基于光伏阵列数学模型，在Matlab中使用电流源、电阻、二极管等元件的模型来构建光伏电池模型，并构成光伏阵列进行仿真。该方法较纯数学模型便捷性大大提升，也能够通过波形图更直观地反映输出特性。但是，文献[14-15]中均未考虑温度系数等实际条件下参数的影响，不能很准确地反映光伏阵列的输出特性。

对于已经获得阴影条件下输出特性的光伏阵列，文献[15-16]仅考虑了初次安装条件下光伏阵列的优化设计方法；文献[17]提出了一种光伏阵列自适应可重构方法，但是通过备用光伏组件补偿阴影遮蔽部分光伏阵列的功率输出，增加了系统成本。

针对以上不足，本文提出一种阴影遮蔽条件下光伏阵列的可重构优化配置方法，综合考虑阴影遮蔽和温度系数等实际因素对光伏阵列输出特性的影响，在不增加光伏组件的条件下，基于光伏阵列实际输出特性进行光伏阵列结构的优化配置，以提高光伏发电系统的效率。

1 光伏阵列输出基本特性

光伏发电系统的典型结构如图1所示。

图1 光伏发电系统结构Fig.1 Structure of PV generation system

无论对于单级还是双级功率变换结构，均需要实现最大功率点跟踪（MPPT）控制以保证光伏阵列能够输出一定光照和温度条件下的最大功率，因此，如何获取实际应用条件下光伏阵列的输出特性，对于MPPT控制算法设计及提高光伏输出效率十分重要。

1.1 阴影遮蔽条件下光伏阵列基本特性

在一定温度与光照条件下，光伏电池输出电压在一个特定工作点对应其最大输出功率，这一点被称为最大功率点。光伏阵列的基本输出特性可以分别用P-U特性和I-U特性来表述输出功率、电流与输出电压之间的关系[18]。本文以如图2所示的6×6串并联结构光伏阵列为对象，分析理想光照条件下与不同阴影遮蔽条件下光伏阵列的输出特性。

需要说明的是，阵列中每串均有一个防逆流二极管，防止各串输出电压不均等时出现逆流现象；且每个光伏组件均并联一个反向续流二极管，在串内组件生成电流不均等时可以起到续流作用。

为了便于分析，设定正常光照条件下光照强度为1000 W/m2，阴影条件下光照强度为400 W/m2，考虑到阴影部分与正常光照部分之间存在过渡区域，可设定两种过渡带光照强度分别为600 W/m2和800 W/m2。基于图2所示光伏阵列结构（每列为光伏组件串联，每行为不同列并联关系），对比无阴影、有阴影及有过渡带的光伏阵列输出特性，阴影分布类型如图3所示。

图2 光伏阵列结构Fig.2 Structure of PV array

图3 不同层级阴影分布示意图Fig.3 model of different distribution levels of shade

四种阴影条件下的输出特性（I-U特性和P-U特性）如图4和图5所示。

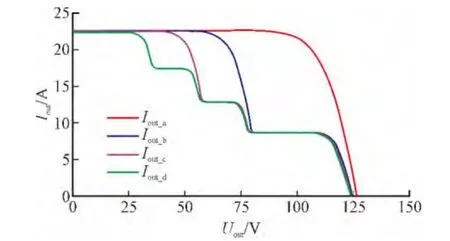
图4 不同层级阴影分布条件下光伏阵列I-U特性Fig.4 I-U characteristics of PV array in different distribution levels of shade

图5 不同层级阴影分布条件下光伏阵列理想输出总功率及P-U特性Fig.5 Total output power and P-U characteristics of PV array in different distribution levels of shade

由图4得到的I-U特性曲线可以看出，较无阴影理想光照条件相比，多层阴影会导致I-U特性出现多个阶梯，反映到P-U特性即为输出功率的多极值性。图5反映了4种阴影条件下光伏阵列理想输出总功率Psum（所有光伏组件在当前光照条件下理想输出功率之和）与实际的输出功率特性曲线，可以看出阴影层数越多输出功率特性曲线的极值越多、特性越复杂。具体计算结果如表1所示。

由表1可以得到，随着阴影层数增多理想输出总功率逐渐减小，而极值点逐渐增多，输出特性更加复杂，进而导致输出效率的降低；另外多个极值点间输出电压差异较大，最大功率点电压较无阴影情况下会有很大变化。

表1 不同层级阴影分布光伏阵列输出特性Tab.1 Output characteristics of PV array in different distribution levels of shade

1.2 考虑温度系数影响的光伏阵列输出特性分析

温度系数是表征光照对光伏组件表面温度影响的重要参数。文献[14-16]并未考虑温度系数对光伏组件表面温度的影响，而实际应用中，光伏组件表面温度对光伏组件的输出特性有较大影响[19]。因此，本文将考虑在无阴影和有阴影两种情形下（如图3中（a）和（d））分析光伏组件表面温度对输出特性的影响。这里光照对光伏电池表面温度的影响是通过温度系数KS来体现的，KS有公式：

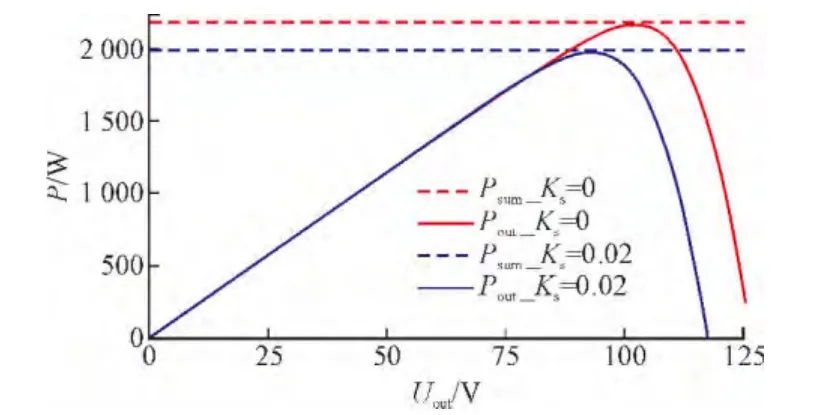
图6 无阴影条件下KS=0及KS=0.02时P-U特性曲线Fig.6 Output characteristics of PV array in no-shade condition when KS=0 and KS=0.02

式中，Ta为环境温度；S为光照强度，W/m2；T为光伏组件表面温度。T的变化对光伏组件输出特性有直接影响。这里根据经验取KS=0.02并与不考虑温度系数（即KS=0）的情况对比，光伏阵列输出特性曲线如图6—7所示，输出特性计算结果如表2所示。

由图6、图7及表2可知，加入温度系数KS后，理想输出总功率有所降低，实际最大输出功率也相应降低，最大功率点电压也相应发生了变化。

2 阴影条件下光伏阵列结构优化规则分析

图7 三层阴影条件下KS=0及KS=0.02时P-U特性曲线Fig.7 Output characteristics of PV array in three levels shade condition when KS=0 and KS=0.02

为了更好地实现光伏最大功率点跟踪控制，提高光伏系统发电效率，本文综合考虑局部阴影遮蔽及温度系数对光伏阵列输出特性的影响，归纳光伏阵列在相同结构条件下，不同阴影遮蔽分布时的输出特性，为光伏阵列结构可重构优化配置提供参考依据。

表2 温度系数对输出特性影响Tab.2 Effects of temperature factors on output characteristics

2.1 多阴影数条件下阵列输出特性分析

根据光伏阵列内不同组件的串并联结构关系，各种阴影遮蔽情况可以简化为以下几种基本阴影分布模型（如图8所示）。为了更接近实际情况，在阴影部分（400 W/m2）与自然光照部分（1000 W/m2）之间模拟一个过渡带（600 W/m2），对相同阴影数量（12块阴影及6块过渡阴影）不同阴影分布的输出特性进行分析。

图8 多阴影数条件下阴影分布类型Fig.8 Different distribution models in the large shade unit numbers

图8中（a）为12块阴影均匀分布在6串当中，情形（b）为12块阴影集中在3串中，情形（c）和（d）分别为偏向于横、纵两个方向的角集中分布。4种阴影分布条件下输出特性如图9和表3所示。

从图9和表3可以看出，对于同样的阴影遮蔽数目，四种阴影分布情况具有相同的理想输出总功率，但实际功率输出特性有很大差异：情形（b）中阴影集中串联分布（集中分布在少数串中）输出特性最为理想，效率最高，且只有一个极值点，与无阴影条件下输出特性（理想情况）相比，最大功率点电压变化很小（见表2与表3）；情形（a）即阴影均匀分布条件下（均匀分布在各串中），P-U特性含有3个极值点，输出效率大幅降低，且最大功率点电压偏移较大；情形（c）和（d）的角集中分布中，P-U特性比较复杂，均出现多个极值点，效率也大幅降低，对比（c）与（d）可以看出：情形（c）的阴影分布相对于情形（d）更接近集中分布，而情形（c）也具有更高的输出效率。综合以上结果，可以看出：相同数目阴影遮蔽时阴影集中串联分布具有较好的输出特性。

图9 多阴影数条件下P-U特性曲线Fig.9 P-U characteristics in the large shade unit numbers

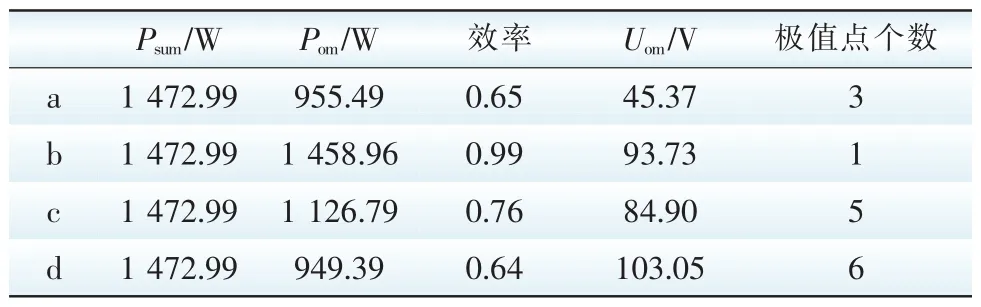
表3 多阴影数条件下光伏阵列输出特性Tab.3 Output characteristics in the large shade unit numbers

2.2 少阴影数条件下阵列输出特性分析

对于实际中很常见的带状阴影和点状阴影（少阴影遮蔽单元数），通过串并联等效关系可以归纳为两种基本的阴影分布如图10所示。

图10 少阴影数条件下阴影分布类型Fig.10 Different distribution models in the few shade unit numbers

两种阴影分布条件下输出特性如图11和表4所示。

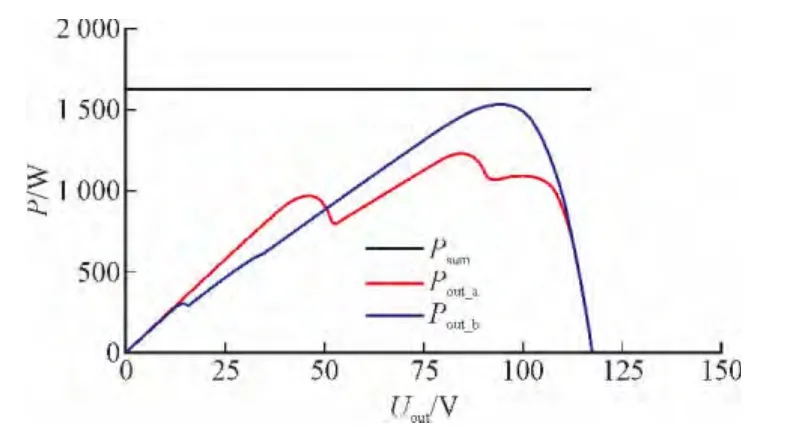
图11 少阴影数条件下P-U特性曲线Fig.11 P-U characteristics in the few shade unit numbers

表4 少阴影数条件下光伏阵列输出特性Tab.4 Output characteristics in the few shade unit numbers

由图11及表4可以看出，两种情况都具有多极值性，但图10（b）的输出特性更接近无阴影的情况，且具有更高的输出功率和效率，最大功率点电压也更接近无阴影条件。

综合以上结果，可以看出：阴影分布与光照强度均不规则，在相同数目阴影遮蔽时阴影集中串联分布具有较好的输出特性。这一结论将为光伏阵列结构优化设计提供重要参考依据。

3 局部阴影条件下光伏阵列优化配置方法

为了实现光伏阵列在阴影遮蔽条件下输出最大功率，需要对阵列的结构进行优化设计。传统方法采用固定式阵列设计方法，即在安装初期需要对安装环境下的光照条件进行勘测，获取日常出现的阴影方向、形态，然后设计光伏阵列的布局，安装后串并联结构固定不变，这种方法在阴影遮蔽条件发生变化时不能动态调整光伏阵列结构以改善其输出特性。

为了克服固定式光伏阵列设计的不足，本文提出一种可重构光伏阵列优化配置方法，其基本思想是将光伏阵列中的光伏组件配以继电器开关，通过对继电器开关网络的控制实现光伏阵列中串并联拓扑的任意转换，以实时适应当前阴影分布条件，改善阵列输出特性的多极值性，保证最大功率输出，并同时尽量减小输出电压变化范围[20]。可重构阵列示意图如图12所示，图中每个开关的位置代表一个光伏组件及其继电器。

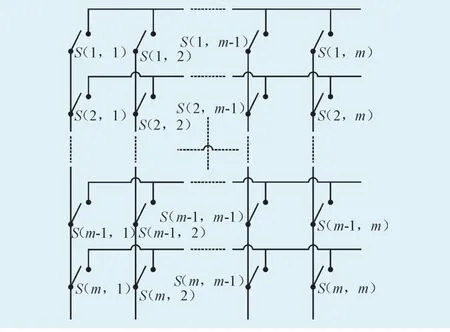
图12 开关阵列示意图Fig.12 model of switch array

可重构光伏阵列优化配置基本规则如下：

1）在光伏组件总数确定的情况下，光伏阵列串并联拓扑的改变必须满足对串联组件个数的要求，以保证输出电压在逆变器输入允许范围。

2）在已知阴影遮蔽条件下，光伏阵列遮蔽部分尽可能按照阴影集中串联分布进行配置。

3）针对可重构光伏阵列设计，在光伏阵列安装初期，尽可能获取阴影日常运动规律，以降低阵列重构程序设计的复杂性。

4）在实际应用中，需要监测光伏组件工作状态、阴影条件、表面温度等，并以此为依据对当前时段的拓扑进行局部调整和优化，尽量以更高的效率输出功率，从而实现智能化的光伏阵列重构优化配置。

基于以上优化配置规则，这里针对不规则阴影分布条件下光伏阵列可重构优化配置的可行性进行了初步验证。针对L型阴影，阵列拓扑如图13所示，采用固定式结构（串并联关系不变）有（a）、（b）两种安装方式。利用可重构优化规则，改变阵列串并联结构使阴影遮蔽部分光伏组件全部串联，形成如图13（c）的拓扑结构。

光伏阵列优化配置前后输出特性及计算结果分别如图14及表5所示。

由图14和表5可以看出，相对于固定式阵列结构（a）和（b），经过重构优化后的结构（c）输出功率有所提升，且输出特性呈现单极值性；与无阴影条件下输出特性（理想情况，见表2）相比，最大功率点电压变化更小。由此可见，光伏阵列可重构优化配置可以改善其输出特性，进一步提高了输出功率和效率。

图13 针对L型阴影的三种阵列结构Fig.13 Three structures of array in L-shape shade

图14 L型阴影P-U特性曲线Fig.14 P-U characteristics of L-type shade

表5 L型阴影输出特性Tab.5 Output characteristics of L-type shade

在L型阴影的基础上，针对实际中可能出现的复杂阴影遮蔽情况（如图15（a）、（b）两种安装方式中所示的角集中型阴影），可重构优化后生成了如图15（c）所示的串并联拓扑结构。

光伏阵列优化配置前后输出特性及计算结果分别如图16及表6所示。

从图16及表6可以得到，在角集中型阴影分布条件下，可重构阵列生成如图15（c）所示的阵列结构输出功率有明显提高，输出特性也呈现单极值性；最大功率点电压变化不大，进一步提高了光伏发电系统的效率。

综合以上结果，光伏阵列优化后最大输出功率得到提升且输出特性呈现单极值性，从而可以简化MPPT算法；另外，阵列优化后最大功率点电压变化幅度不大，降低了光伏功率变换器对输入电压控制的要求。

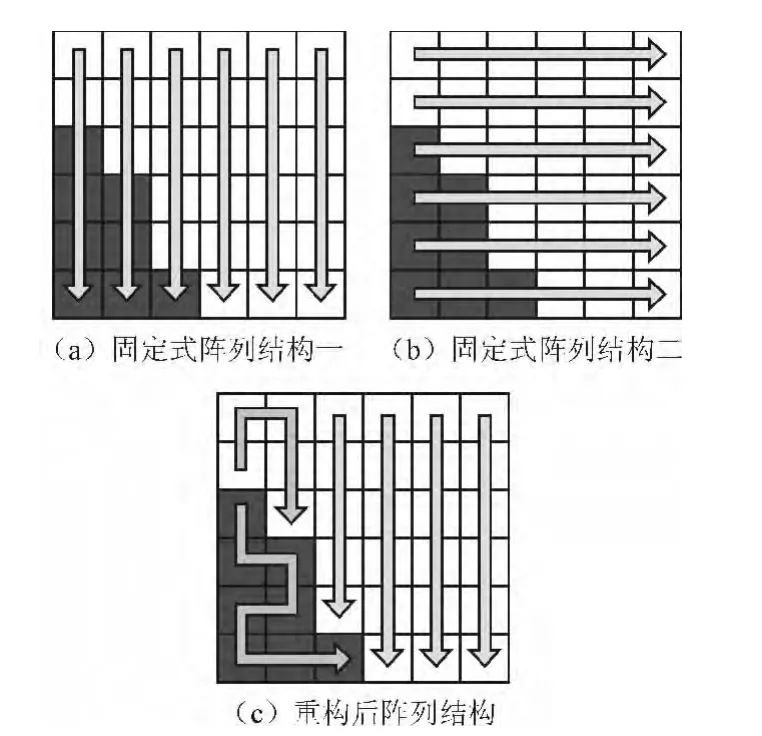
图15 针对角集中型阴影的三种阵列结构Fig.15 Structures of array in corner-concentrated shade

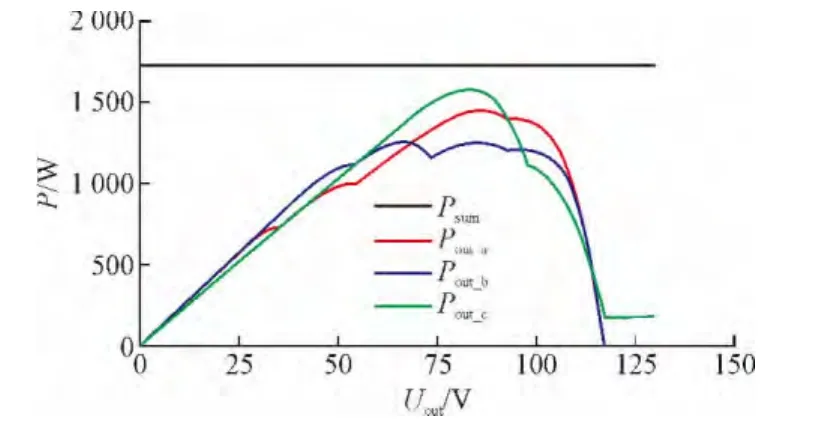
图16 角集中型阴影P-U特性曲线Fig.16 P-U characteristics of corner-concentrated shade

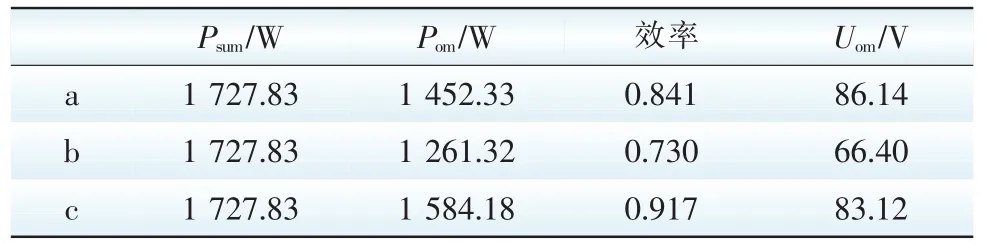
表6 角集中型阴影输出特性Tab.6 Output characteristics of corner-concentrated shade

4 结论

本文结合表面温度系数对光伏阵列特性的影响，对阴影遮蔽条件下光伏阵列的输出特性进行了研究与分析，并提出了一种光伏阵列可重构优化配置方法，以提高光伏发电系统效率。从研究结果可以得出以下结论：

1）局部阴影的多种分布方式可简化为几种典型的阴影分布模型，其输出特性带来的影响主要体现为功率-电压输出特性的多极值性、最大输出功率的降低和最大功率点电压的偏移。

2）不同深度的阴影会造成光伏阵列不同区域内温度变化，进而对输出特性造成影响，因此考虑温度系数影响更符合实际情况。

3）相同阴影数目条件下，依据阴影集中串联分布原则进行光伏阵列可重构优化设计，可以有效改善光伏阵列的输出特性。

4）光伏阵列优化后输出特性呈现单极值性，有利于简化MPPT算法；并且优化后最大功率点电压变化幅度较小，易于实现光伏功率变换器输入电压控制，验证了智能化可重构阵列对输出特性改善和效率提升的可行性和有效性。

[1] 赵争鸣，雷一，贺凡波，等．大容量并网光伏电站技术综述[J]．电力系统自动化，2011，35（12）：101-107．ZHAO Zhengming，LEI Yi，HE Fanbo，et al．Overview of large-scale grid-connected photovoltaic power plants[J]．Automation of Electric Power Systems，2011，35（12）：101-107（in Chinese）．

[2] 海涛，刘得刚，骆武宁，等．一种太阳能光伏并网逆变器的研究[J].陕西电力，2010，38（1）：49-52．HAI Tao，LIU Degang，LUO Wuning，et al.Research on solar photovoltaic grid-connected inverter[J].Shaanxi Electric Power，2010，38（1）:49-52（in Chinese）．

[3] 赵春江，杨金焕，陈中华，等．太阳能光伏发电应用的现状及发展[J]．节能技术，2007（5）：461-465．ZHAO Chunjiang，YANG Jinhuan，CHEN Zhonghua，et al．State& development of photovoltaic application[J]．Energy Conservation Technology，2007（5）：461-465（in Chinese）．

[4] 刘观起，游晓科，杨玉新，等．光伏发电系统最大功率点跟踪方法研究综述[J].陕西电力，2012（2）：18-22．LIU Guanqi，YOU Xiaoke，YANG Yuxin，et al．Study on maximum power point generation system[J]．Shaanxi Electric Power，2012（2）：18-22（in Chinese）．

[5] 周倩，薛建，于辰．基于Matlab的光伏并网系统的仿真分析[J]．陕西电力，2012，40（3）：19-22.ZHOU Qian，XUE Jian，YU Chen．Analysis and simulation for grid-connected photovoltaic system based on matlab[J]．Shaanxi Electric Power，2012，40（3）：19-22（in Chinese）．

[6] 刘承佳，李鹏，李婉娉，等．智能电网中光伏发电MPPT仿真分析[J]．陕西电力，2011（12）：31-35．LIU Chengjia，LI Peng，LI Wanpin，et al．Simulation analysis on photovoltaic generation with MPPT in smart grid[J]．Shaanxi Electric Power，2011（12）：31-35 （in Chinese）．

[7] 曹冲，卢永杰，佘小莉，等．智基于改进扰动法的光伏电池最大功率点跟踪研究[J]．陕西电力，2011（12）：62-67．CAO Chong，LU Yongjie，SHE Xiaoli，et al．Probe into photovoltaic cell maximum power point tracking based on improved perturbation method[J]．Shaanxi Electric Power，2011（12）：62-67（in Chinese）．

[8] 翟载腾，程晓舫，丁金磊，等．被部分遮挡的串联光伏组件输出特性[J]．中国科学技术大学学报，2009，39（4）：398-402．ZHAI Zaiteng，CHENG Xiaofang，DING Jinlei，et al．Characteristics of partially shadowed serial PV module output[J]．Journal of University of Science and Technology of China，2009，39（4）：398-402（in Chinese）．

[9] 徐保友，黄挚雄，焦晓雷．局部阴影下光伏阵列的建模与仿真分析[J]．电网与清洁能源，2012（4）：73-76．XU Baoyou，HUANG Zhixiong，JIAO Xiaolei．Modelbuilding and simulation analysis of photovoltaic arrays under partial shadow effects[J]．Power System and Clean Energy，2012（4）：73-76（in Chinese）．

[10]戚军，张晓峰，张有兵，等．考虑阴影影响的光伏阵列仿真算法研究[J]．中国电机工程学报，2012（32）：131-138．QI Jun，ZHANG Xiaofeng，ZHANG Youbing，et al．Study on simulation algorithm of PV array considering shade effect[J]．Proceedings of the CSEE，2012（32）：131-138（in Chinese）．

[11]朱啸行，袁越，傅质馨．考虑多点局部阴影的光伏阵列建模及复合型最大功率跟踪算法研究[J]．电网与清洁能源，2012（9）：56-61，67．ZHU Xiaoxing， YUAN Yue， FU Zhixin．Modeling of photovoltaic array with multi-partial shadows and study of the hybrid maximum power point tracking algorithm[J]．Power System and Clean Energy，2012（9）：56-61，67（in Chinese）．

[12]JI Y H，JUNG D Y，WON C Y，et al．Maximum power point tracking method for PV array under partially shaded condition[C]//Energy Conversion Congress and Exposition，2009．ECCE 2009．IEEE．IEEE，2009：307-312．

[13]LEI P，LI Y，SEEM J E．Sequential ESC-based global MPPT control for photovoltaic array with variable shading[J]．Sustainable Energy，IEEE Transactions on，2011，2（3）：348-358．

[14]刘邦银，段善旭，康永．局部阴影条件下光伏模组特性的建模与分析[J]．太阳能学报，2008，29（2）：188-192．LIU Bangyin，DUAN Shanxu，KANG Yong．Model and analysis of characteristics of PV module with partial shading[J]．Acta Energiae Solaris Sinica，2008，29（2）：188-192（in Chinese）．

[15]刘晓艳，祁新梅，郑寿森，等．局部阴影条件下光伏阵列仿真模型的研究[J]．系统仿真学报，2012，24（5）：1125-1131．LIU Xiaoyan，QI Xinmei，ZHENG Shousen，et al．Study on simulation model of PV array under partially shading[J]．Journal of System Simulation，2012，24（5）：1125-1131（in Chinese）．

[16]肖景良，徐政，林崇，等．局部阴影条件下光伏阵列的优化设计[J]．中国电机工程学报，2009，29（11）：119-124．XIAO Jingliang，XU Zheng，LIN Chong，et al．Optimal design of photovoltaic arrays under partial shading[J]．Proceedings of the CSEE，2009，29（11）：119-124（in Chinese）．

[17]NGUYEN D，LEHMAN B．A reconfigurable solar photovoltaic array under shadow conditions[C]//Applied Power Electronics Conference and Exposition，2008．APEC 2008．Twenty-Third Annual IEEE．IEEE，2008：980-986．

[18]峁美琴，余世杰，苏建徽．带MPPT功能的光伏阵列matlab通用仿真模型[J]．系统仿真学报，2005，17（5）：1248-1251．MAO Meiqin，YU Shijie，SU Jianhui．Versatile matlab simulation model for photovoltaic array with MPPT function[J]．Journal of System Simulation，2005，17（5）：1248-1251（in Chinese）．

[19]张化德．太阳能光伏发电系统的研究[D]．济南：山东大学，2007．

[20]NGUYEN D，LEHMAN B．An adaptive solar photovoltaic array using model-based reconfiguration algorithm[J]．Industrial Electronics，IEEE Transactions on，2008，55（7）：2644-2654．