基于RBF神经网络的交通生成预测模型

邓 捷，陆百川，刘权富，张 凯，马庆禄

（重庆交通大学交通运输学院，重庆 400074）

交通生成预测是通过预测算法，对城区社会经济特性、土地利用形态和居民个人及家庭属性进行综合分析，准确预测出对象地区未来的交通生成量，是正确进行交通宏观决策，制定交通发展战略，编制交通规划，以及制定道路可行性研究的重要前提。但是，由于影响交通生成量的因素较多，且各种因素之间的关系复杂，需要建立一个能包含所有影响因素的高精度预测模型，以使未来交通生成量的预测达到理想效果，这对交通规划具有重要的意义。

许多研究者进行了有关交通生成预测的研究，常见的有生成率模型、类别生成率模型、回归分析模型和类别回归分析模型等［1－4］，这些模型从简单到复杂，就其中具体利用何种方法建立模型，主要取决于对象区域的土地利用形态和社会经济特征，这些模型属于利用区域某一整体属性为依据的集计模型，因此该类模型缺少影响交通生成的行为基础这一主要因素，导致预测结果与实际值相差较大，不能满足实际应用的需要。在其后的研究中为克服集计模型缺陷，研究者们建立了随机效应模型、混合仿真模型和BP神经网络模型等［5－7］，这些是以离散数据为基础的离散模型，不仅拥有集计模型分析的优势，还能有效分析交通管理政策对交通出行者的影响，成为当前分析交通生成的主要模型。但是前面两种离散模型对数学推导要求较高，导致建模过程复杂，不利于实际操作，而BP神经网络模型，在学习过程中存在多个最佳逼近点，预测过程慢，以及预测结果与实际情况相差大等缺陷，不适宜实际应用［8］。随着RBF神经网络技术的不断成熟，充分利用RBF神经网络能无限逼近任何非线性映射关系，进行交通方面的研究已成为一种有效方法［9－10］。RBF神经网络具有成形的系统算法结构，不需要再利用数学公式推导，同时它是利用输入和输出的数据学习有用的知识，适合对无规则和多约束问题的研究，也是一种前馈式网络结构，适合多变量函数的逼近，具有唯一最佳逼近点，其独有的容错性和泛化能力能较好地进行预测。笔者以离散数据为基础，利用RBF神经网络进行研究，建立了基于RBF神经网络的交通生成预测模型。利用该模型进行交通生成预测，根据城区历史交通生成量，对其交通生成量的形成规律进行判断和学习，从而对未来交通生成量作出准确预测。

1 RBF神经网络原理模型及算法

RBF神经网络是一种具有拓扑结构的前馈式神经网络，由3层结构组成，包括输入层、隐含层和输出层。RBF神经网络拓扑结构如图1所示。

图1 RBF神经网络拓扑结构

输入层的作用是把来自外部的数据映射到隐含层，输入层与隐含层实现神经网络的非线性映射，不对数据进行任何处理。整个神经网络的中心处理层是隐含层，隐含层与输出层实现神经网络的线性映射，由于隐含层里包含径向对称的径向基函数，隐含层提供给输出层的数据在径向基函数作用后才输出。

最初隐含层的作用函数对输入数据只在局部响应，当输入数据接近作用函数的中央范围处时，隐含层就会产生较大的输出。径向基函数采用高斯函数:

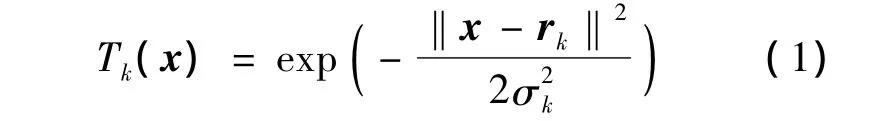
式中:x为输入向量；rk为隐节点的中心；‖x－rk‖为向量x－rk的范数；σk为第k个感知的变量，它决定该基函数围绕中心的宽度。

由于高斯径向基函数自身具有特殊的性质，使其能对输入变量某一范围具有选择性的反应能力，从而实现RBF神经网络的局部调谐能力。

选择输出层作用函数为求和函数时，输出为:

式中:Wjk为网络的输出权值；N为感知单元的个数（隐含层节点数）；Tk为径向基神经元。

利用RBF神经网络进行预测时，需要对基函数的中心、方差和隐含层与输出层间的权值进行学习。学习的方法很多，基于研究的需要，采用自组织选取中心法进行学习。

2 交通生成预测模型建立

2.1 交通生成量的影响因素

在分析交通量产生因素时，必须将宏观的区域影响和微观的个人及家庭影响同时考虑。如交通形成与土地利用之间的关系，交通小区内住宅区是重要的交通发生源，大型工厂的存在、机关事业单位片区、各类型学校的拥有量和商业圈中心等都是交通量形成的主要原因。从宏观和微观分别进行分析，宏观的区域影响主要指的是交通小区内用地情况、小区在城市中的地理位置、工作人员拥有量、各种人口总数、学生数量、工作岗位等居民特征和居民收入等社会发展水平，这两类影响因素变化量不会很大，但类型繁多。微观的个人及家庭影响主要指的是年龄、性别、职业、职务、自由时间、家庭职责、驾照拥有量和家庭规模，家庭收入、家庭人口构成和家庭交通工具拥有率等是交通量形成的基础，且这两类影响因素变化量较大，类型也繁多。

2.2 参数量化处理

影响交通生成的因素中，存在数值型和非数值型两种类型的参数，而最后结果需要的是总人口数量，不是具体某个参考因素，因此模型输入参数可以在同一参考因素具有多个特征值时进行相同的变换，且不会影响模型的预测结果。根据模型对输入参数的需求，数值型参数可以直接用作模型的输入参数，如人口总数、学生数量、工作岗位、年龄等；非数值型参数需要进行量化处理，通过量化后再作为模型的输入参数。为了便于数据处理，根据实际情况，将性别进行量化处理，用0代表男，1代表女。其他的非数值参数采取同样的处理方式进行量化。

2.3 基于RBF神经网络的交通生成预测模型

对选定预测区域内交通生成量的影响因素数据进行分析和整理，将各种影响因素分类作为模型的输入，并将输入分成不同的大类，包括选定对象地区的人口、土地利用形式、各项经济指标等，便于模型输入进行参考。将预测区域交通生成量作为输出，为简化模型，对输出进行归类，输出结果为各种目的出行次数的集合。通过上述分析，根据输入参数和对应的输出，假设存在关系式为:

式中:xm，t为土地利用形态影响因子；ym，t为社会经济特性影响因子；zm，t为个人及家庭特性影响因子；T（k）为交通生成总量；m为大区数目。

式（3）中的S为RBF神经网络进行预测的切入点，通过RBF神经网络内部求得S，就能预测求出未来交通生成量。因此，依靠原始模型样本训练得到可靠关系式S是整个模型的重点所在。在样本训练过程中，为保证预测精度，定义预测指标函数为:

对于单目标函数n=1，标定的目标是调整Wjk，使误差 e最小，即:

则权因子的调节公式为:

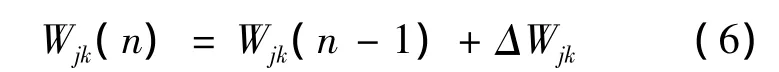
交通生成预测的原始RBF神经网络模型如图2所示。在进行原始RBF神经网络模型训练时，整个过程是通过神经元实现，因此，每个阶段都有相对应的神经元去参与处理。输入层的每种影响因素都存在一个神经元与其相互对应，以编号1～52表示输入层的神经元，编号53～54表示输出层的神经元。隐含层也存在大量的神经元，RBF神经网络训练时隐含层神经元由模型系统根据训练目的自身确定，因此隐含层的神经元不需要人为确定，而由模型自身确定其数量。前面将模型的输出进行了合并，因此输出层只存在两个神经元。

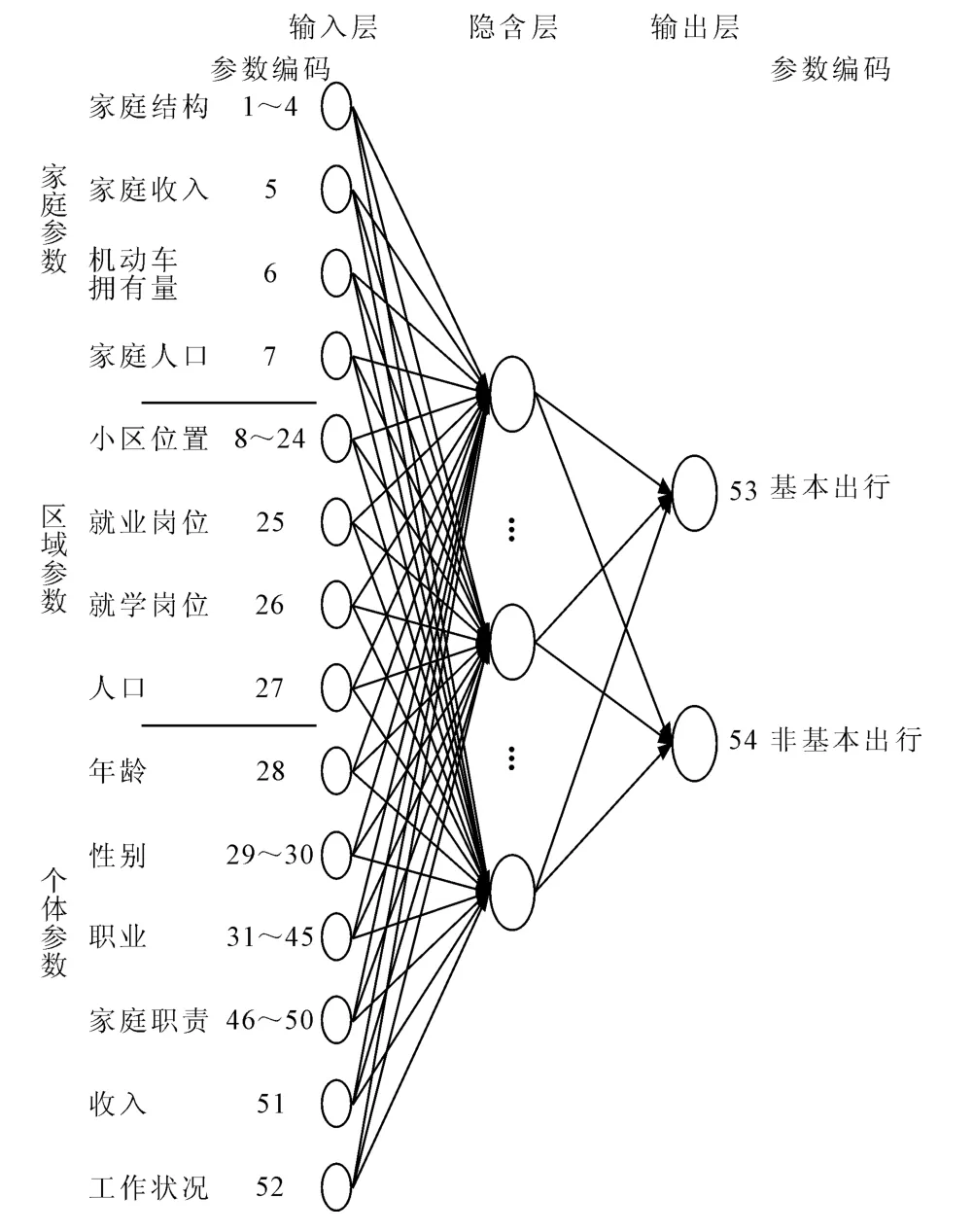
图2 交通生成预测的原始RBF神经网络模型

在原始RBF神经网络训练成功的状态下，将需要预测区域的影响因素作为输入参数，并输入到训练好的原始RBF神经网络中，通过RBF神经网络的处理，实现对未来交通生成量的预测，得到区域未来交通生成量T（k+1）。整个模型预测过程如图3所示。

2.4 具体算法步骤

（1）选择与出行生成相关性较强的原始数据，将其作为样本训练数据和预测数据；

（2）对数据进行归一化处理，使其变换为RBF神经网络需要的输入模式；

（3）构建RBF神经网络，并定义网络的相关参数；

（4）调整隐含层单元数和隐含层单元中心，用高斯函数计算隐含层权值，获得隐含层输出；

（5）通过隐含层与输出层的函数关系得出输出层的输出；

（6）计算训练误差；

（7）判断训练误差是否小于指定目标，是则转到步骤（9），否则转步骤（8）；

（8）利用最小二乘法进行权值调整，修改输出层权值，转入步骤（6）；

（9）全部样本是否训练完成，是则进行下一步，否则返回步骤（4）；

（10）利用神经网络对用于检验网络性能的归一化处理数据进行预测；

（11）对预测得到的数据进行反处理，获得真实预测值，并计算误差。

3 仿真实例

3.1 模型数据设定

选择重庆市江北区人口调查数据为模型仿真数据，该调查数据包含了该区常住人口的一日出行情况，以及每个片区土地利用状况和社会经济情况。为了仿真需要，根据实际情况，按交通小区把调查对象分为153个小区，共包括13429户家庭和46591个人的一日出行情况。其中调查内容包括每个小区出行者家庭结构、个体特性、出行目的、出行时间和出行方式，同时还调查出发地和目的地土地利用形态等特征。

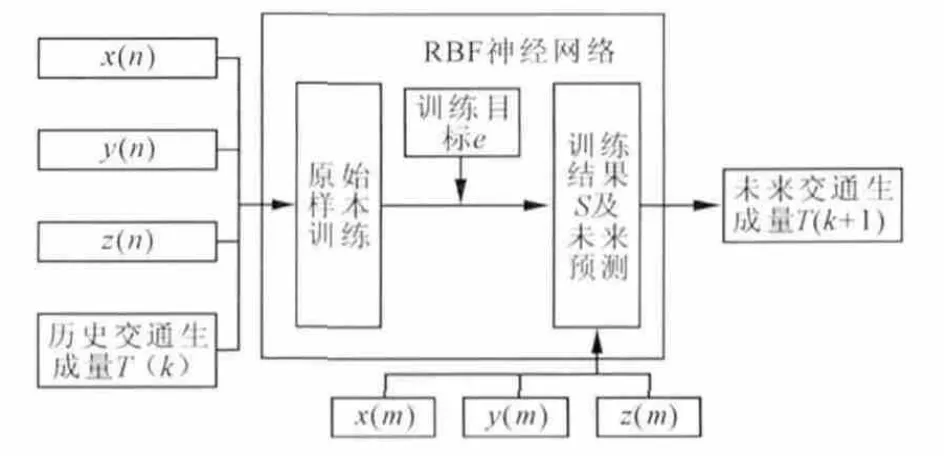
图3 基于RBF神经网络的交通生成预测过程

首先需要对原始调查数据进行预处理和分析，主要分两个方面:①调查对象的属性，主要有小区位置、人口总数、就业人数、学生人数、家庭结构、家庭收入、家庭人口、交通工具和数量、性别、年龄、职业、家庭职责、收入等构成的原始数据库；②出行目的合并，根据调查得到的出行结果，结果合并为基本出行（上班、上学）和非基本出行（购物、探亲访友、娱乐、旅游、就医、文化娱乐等）。

3.2 误差指标定义

相对误差绝对值的平均值为:

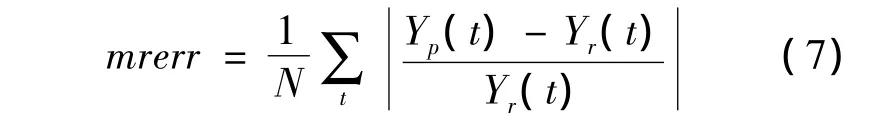
相对误差绝对值的最大值为:

均方根误差为:

式中:Yp（t）为交通生成量的预测值；Yr（t）为交通生成量的实际值。

3.3 模型数据的预处理

为使数据适合RBF神经网络特性，减小噪声干扰，先对样本数据进行归一化处理，其公式为:

式中:Xmax、Xmin分别为各因子的最大值和最小值；X为因子值。

3.4 模型应用与仿真

基于预测模型对数据的需要，将获得的数据分为训练与测试两个样本集合。为提高预测精度，在数据划分时增加训练样本的数据容量，以便加强对模型训练检验，其中随机选择60%的数据为训练样本，余下40%的数据为测试样本。

3.5 仿真结果及分析

现将随机选取的92个小区作为训练样本，剩下的61个小区作为测试样本。经过预测模型处理，将测试样本数据与实际数据进行比较分析，仿真结果及误差如图4所示。

从图4可以看出，基于RBF神经网络的预测模型能成功地进行交通生成量的预测，除少部分数据误差较大外，其余误差都很小。

为了与RBF神经网络预测模型进行对比，利用同样以离散数据为基础的BP神经网络进行交通生成预测。对相同的数据进行BP神经网络预测，其隐含层包含45个神经元，预测精度为0.001。将BP神经网络预测与RBF神经网络预测进行对比，两种神经网络的预测误差指标比较如表1所示。

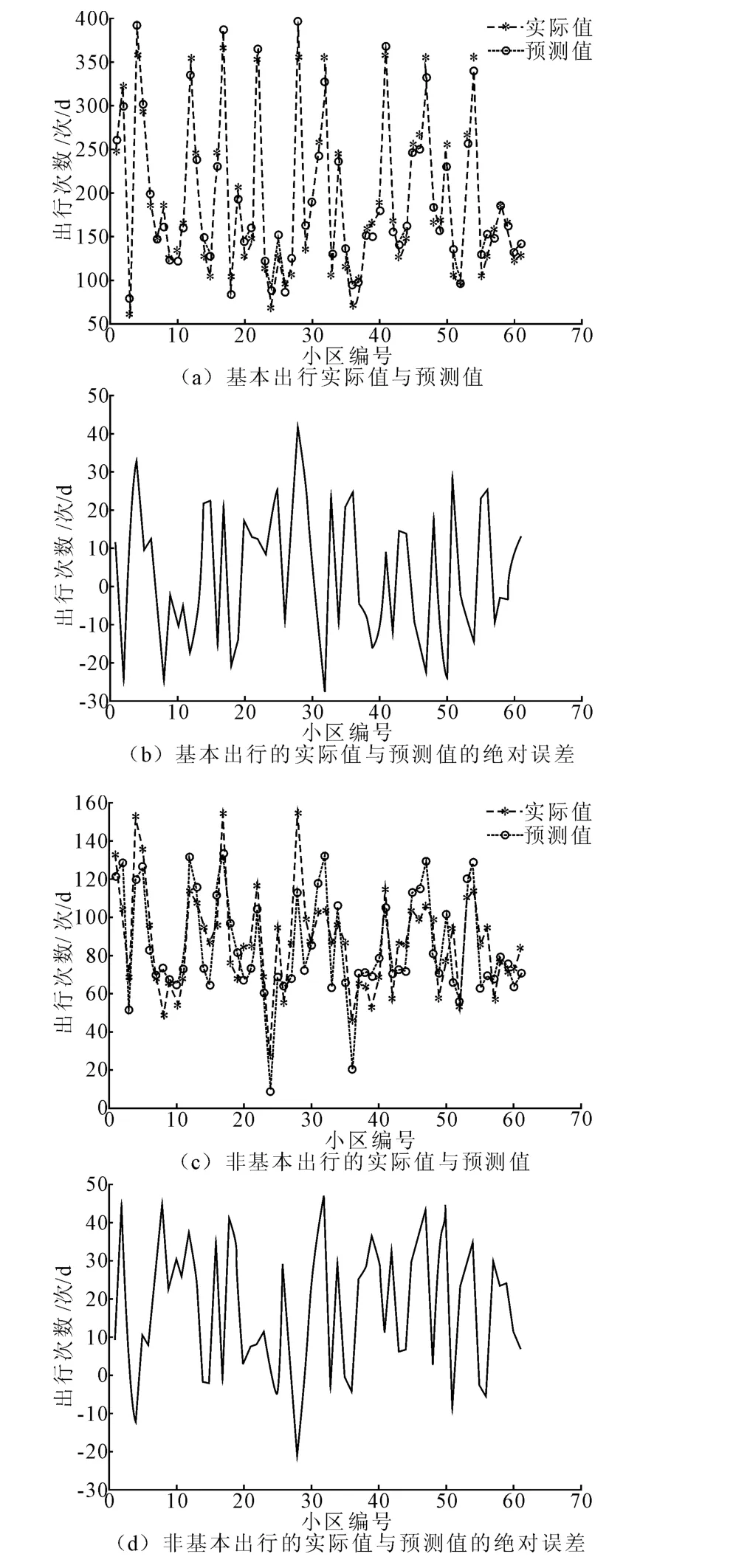
图4 RBF神经网络预测仿真结果及误差

通过两种预测模型预测误差指标对比可知，RBF神经网络的预测精度比BP神经网络的要高，基本出行和非基本出行的实际值与预测值差异要小，能满足交通生成预测的要求。

通过对仿真过程和仿真结果进行分析发现，在利用BP神经网络预测的过程中，由于BP神经网络不存在唯一最佳逼近点，导致需要进行多次预测才能得到最佳预测结果，预测过程繁琐，最佳的预测结果精度较低，与实际值差距大，而笔者提出的RBF神经网络预测模型明显优于BP神经网络预测模型，该交通生成预测方法比传统的交通生成预测方法准确性高，能有效地进行交通生成预测。

表1 两种神经网络交通生成预测误差指标比较

4 结论

通过模型仿真分析，采用RBF神经网络进行交通生成预测是可行的，算法实现简单，充分结合了RBF神经网络自学习、自组织、自适应和大范围数据融合的特性，进行交通生成预测，得到的结果比其他预测模型精度更高，可为交通规划的制定提供更完善和更准确的数据信息。

［1］刘小明，任福田.公路网规划中交通预测的思想方法［J］.中国公路学报，1994，7（3）:54 －59.

［2］石飞，王炜，江薇，等.基于土地利用形态的交通生成预测理论方法研究［J］.土木工程学报，2005，38（3）:115－118.

［3］GEORGE R P.A demand theory for numbers of trips in a random utility model of recreation［J］.Journal of Environmental Economics and Management，1992，2（9）:357－367.

［4］易汉文.城市分析与交通预测［M］.武汉:湖北科学技术出版社，1994:155－180.

［5］高为，陆百川，贠天鹂，等.基于时空特性和RBF神经网络短时交通流预测［J］.交通信息与安全，2011，29（1）:16 －24.

［6］陆化普，周钱.交通出行生成预测的神经网络模型［J］.交通运输工程与信息学报，2008，6（2）:6 －11.

［7］刘洪丽.城市居民出行生成预测方法研究［D］.南京:河海大学图书馆，2006.

［8］欧阳红祥，李欣，张信娟.人工神经网络在建筑材料价格预测中的应用［J］.武汉理工大学学报:信息与管理工程版，2013，35（1）:115 －118.

［9］张冬青，宁宣熙，刘雪妮.基于RBF神经网络的非线性时间序列在线预测［J］.控制理论与应用，2009，26（2）:151－155.

［10］吕晓玲，谢邦昌.数据挖掘方法与应用［M］.北京:中国人民大学出版社，2009:144－149.