基于彩色形态学的图像边缘检测算法
李雪林,彭斯俊,宋晓丽
(武汉理工大学理学院,湖北 武汉 430070)
边缘检测是图像处理与模式识别中一个重要课题,它广泛地应用于图像分割、目标识别和遥感等领域[1-2]。彩色图像比灰度图像包含更丰富的信息,在现实生活中的应用也越来越广。彩色图像中约有90%的边缘与其灰度图像的边缘是一样的,但仍有10%的边缘信息是在灰度图像中检测不到的[3]。因此,对彩色图像边缘信息的研究是近年来研究者关注的前沿课题之一。如ZENG[4]等运用VTV去噪和色差的彩色图像检测方法;MA[5]等提出的基于特征融合的彩色图像边缘检测方法;CHU[6]等运用颜色不变量进行边缘和角点检测方法。然而目前研究者大都是在RGB颜色空间中对图像进行边缘提取的,但RGB空间是一种不均匀、不直观的颜色空间,人们难以将某一RGB值与确定的颜色直观地对应起来,因此,也有研究者选取更加符合视觉感觉的HSI(hue,saturation,intensity)空间进行边缘提取,如高丽等的基于数学形态学HSI空间的彩色边缘检测方法[7]。该算法分别对 H、S、I 3个分量进行边缘信息检测,然后综合处理得到最后的边缘信息,但该算法的抗噪效果不甚理想。基于以上研究,笔者在HSI空间中提出了一种彩色边缘检测算法,并通过相关实验证明了该算法的可行性和适用性。
1 HSI颜色空间形态变换
HSI彩色空间是建立在人类可接受颜色的基础上的,并且其H、S、I 3个分量之间是相互独立的,这便可避免在RGB空间中3个分量存在高度相关性的问题。同时HSI彩色空间具有两个特点:①I分量与图像的彩色信息无关;②H分量和S分量与人类视觉感知颜色的方式紧密联系。这使得它可在彩色图像中消去彩色信息(色调和饱和度)强度分量的影响,使其成为开发基于彩色描述的图像处理的理想工具。由于形态变换注重图像的明暗变化,因此运用HSI颜色空间可以把彩色图像的明暗变化单独用I分量来表示,这可以充分体现出在HSI空间中进行形态变换与灰度形态学的相关性。
1.1 RGB空间与HSI空间的相互转换
经过多年的研究,许多学者已经给出了不同的RGB空间与HSI空间的相互转换方法,常见的有几何推导法、坐标变换法、分段定义法、Bajon近似算法,以及标准模型法。几种方法的比较分析如表1所示。笔者鉴于对分辨率及逆向还原性的考虑,选择几何推导法来实现RGB空间与HSI空间的相互转换。
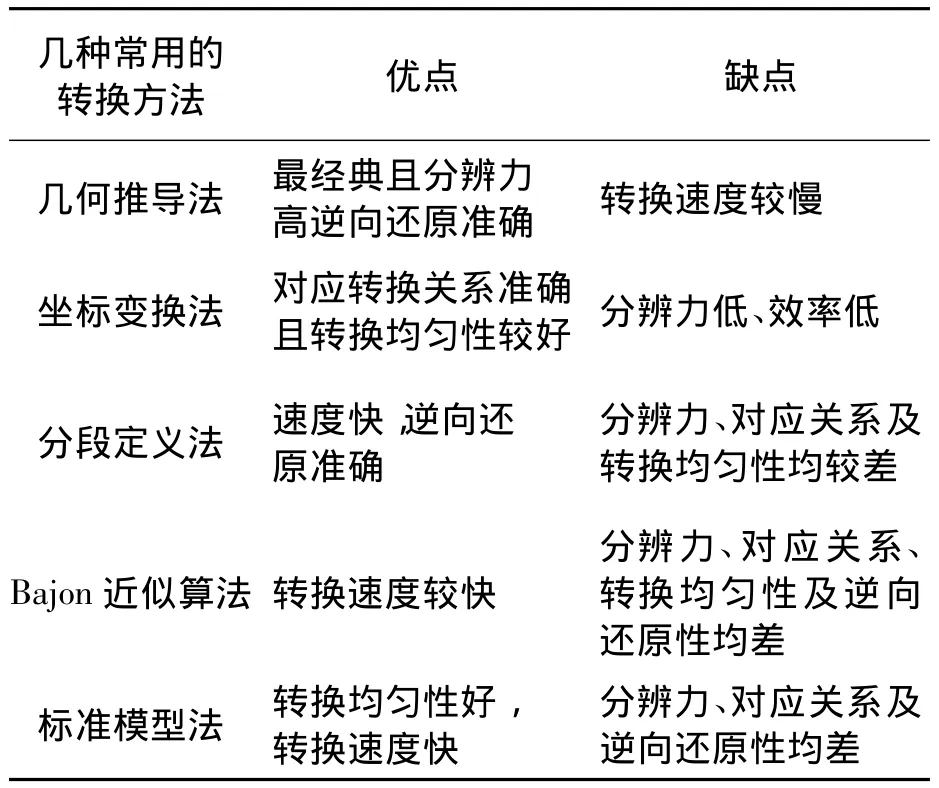
表1 几种常见RGB-HSI相互转换算法的应用比较
1.2 HSI颜色空间形态变换的相关定义
彩色形态膨胀V⊕cB与彩色形态腐蚀VΘcB的定义[8]为:
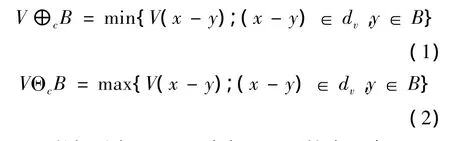
彩色形态开V◦cB和闭V·cB的定义为:

式中:V(x)为HSI空间中的输入图像;B为结构元。
基于以上几种基本的彩色形态学变换,可以相应地得到V(x)关于不同尺度结构元B1、B2的彩色多结构交替顺序开-闭和闭-开滤波算子的定义:
彩色多结构交替顺序形态开-闭滤波算子ASFOCc为:

彩色多结构交替顺序形态闭-开滤波算子ASFCOc为:
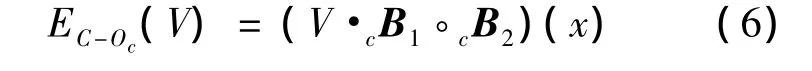
2 多结构多尺度的彩色形态边缘检测
过去大多数形态学边缘检测算法多采用单一的结构元,而单一的结构元很难有效地对复杂的边界信息进行处理。因此笔者采用多结构多尺度结构元的思想来构造彩色形态边缘检测算子,得到的公式如下:
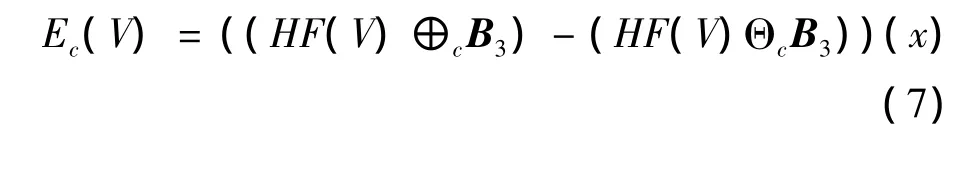
式中:HF(V)为得到的新的混合滤波器(如式(8));B3为结构元。


将式(8)用于平滑图像去除噪声。
由于结构元B1和B2的尺度不一样,尺度小的结构元的去噪能力弱,但能较好地保护图像的细节;而尺度大的结构元却与其相反。因此采用交替顺序滤波就可避免单一使用尺度大或尺度小的结构元的不足,因为它既能滤除噪声又可以保持图像的细节信息;同时依据ASFOCc和ASFCOc在不同强度高斯噪声下的信噪比(PSNR=10×lg( 10+),其中 V(x)、V(x)分0别为原图和加噪图)的大小可以看出:噪声强度在0.01~0.06 之间时,ASFCOc的PSNR 值均高于ASFOCc的相应值;而当噪声强度在0.07~0.09之间时,情况却与之相反。这说明单独使用彩色交替顺序形态开-闭或闭-开算子将不能有效地滤除掉图像中的所有噪声,并且在条件一定的情况下,ASFCOc的抗噪能力略优于ASFOCc。因此笔者经过多次实验研究最后决定将两者按30%和70%的比例进行融合,得到一种新的滤波算子,并通过实验可以看出该滤波算子在不同强度高斯噪声下的信噪比远远高于上述两种算子(信噪比的值越大说明算子的抗噪性能越强),如图1所示。

图1 不同滤波算子得到的图像信噪比比较
笔者引入了一种全方位形态学结构元,其中B31,B32,B33,B34为线性结构元,B35,B36,B37,B38为拐点保护结构元,每一个结构元都可以表示图像某一方向的结构特征。B3i(i=1,2,…,8)的具体形式如图2所示。
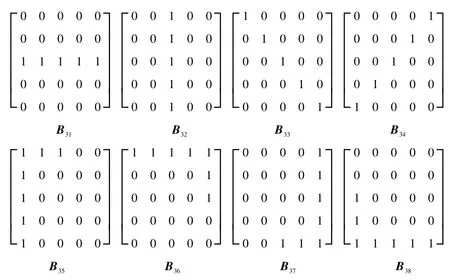
图2 全方位多结构元
同时笔者结合多尺度结构元的思想将B3i经过n次膨胀运算得到结构元nB3i,即:

并用nB3i对图像进行边缘检测,再将其结果叠加得到最后的边缘图像。边缘检测算法的具体实现步骤如下:
(1)将原图像从RGB颜色空间转换到HSI颜色空间。
(2)对HSI颜色空间中的图像用B1和B2进行交替顺序滤波,以滤除噪声。
(3)利用8个不同的全方位形态结构元B3i(i=1,2,…,8)经过 n次膨胀后的结构元 nB3i分别提取图像的边缘,得到:
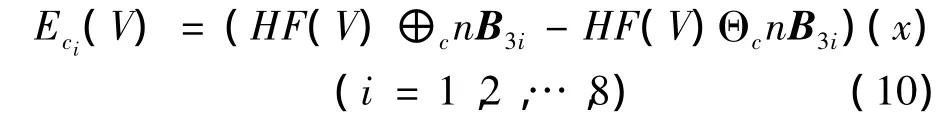
将各尺度下的边缘Eci(V)按照一定的权重进行合成,合成运算式为:
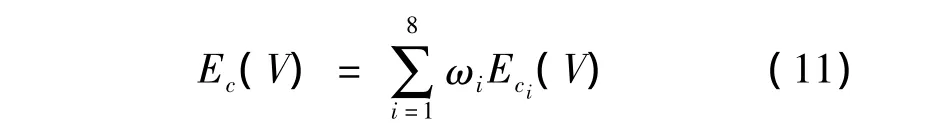
其中,ωi为各尺度的权重系数,计算式如下[9]:
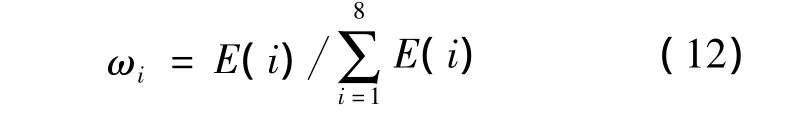
E(i)为用结构元nB3i提取的边缘Eci(V)的信息熵:

[0,l-1]为 HSI空间中 H(x)、S(x)、I(x)各分量按照p(H(x)+S(x))+(1-p)I(x)融合后得到的灰度值范围,p为加权因子,并设定n=0.4,p=0.3;Pi(j)为边缘图像 Eci(V)中融合后的灰度值为j的概率。
(4)把经过边缘检测后的图像从HSI颜色空间中转换到RGB颜色空间中,以便电脑显示。
3 实验及结果分析
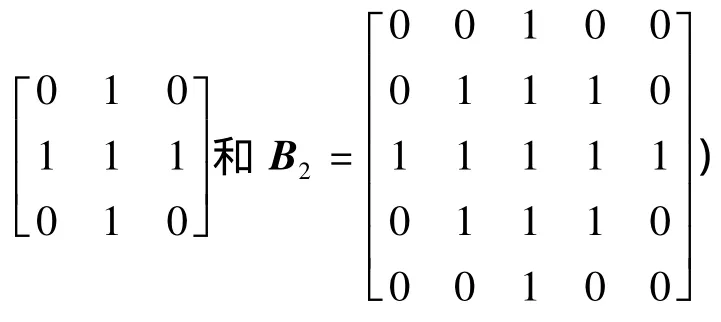

图3 加噪图像边缘检测

图4 笔者算法的图像边缘检测


表2 各种算子边缘提取的RMSE和PSNR对比表
4 结论
笔者基于对彩色图像形态学的研究,提出了一种基于HSI颜色空间的多结构元多尺度的彩色形态学边缘检测算法。不但充分利用了HSI空间的色度、饱和度和亮度信息,而且也充分运用了形态学在图像处理研究中的优势。该方法不仅拓宽了彩色形态学的应用范围,而且通过实验结果可以看出,与其他算法相比,笔者的算法不但有效地抑制了噪声的出现,而且能有效地检测复杂边缘,使检测出的边缘具有良好的完整性和连续性,同时不含伪边缘,为图像的进一步分析与研究奠定了较好的基础。
[1]DESHMUKH K S.Color image segmentation:a review[C]∥Proc.of SPIE.[S.l.]:[s.n],2010:1 -6.
[2]DARDAS N H,GEORGANAS N D.Real-time hand gesture detection and recognition using bag-of-features and support vector machine techniques[J].IEEE Trans Instrumentation and Measurement, 2011,60(11):3592-3607.
[3]NOVAK C L,SHAFER S A.Color edge detection[C]∥Proe of DARPA Image Understanding Workshop,Los Angeles.California:[s.n.],1987:35 -37.
[4]ZENG J,LI D H.Color image edge detection method using VTV denoising and color difference[J].Optik -Internal Journal for Light and Election Optics,2012,123(22):2072- 2075.
[5]MA Y,GU X D.Feature fusion method for edge detection of color images[J].Journal of Systems Engineering and Electronics,2009,20(2):394-399.
[6]CHU J,MIAO J,ZHANG G M,et al.Edge and corner detection by color invariants[J].Optics and Laser Technology,2013(45):756-762.
[7]高丽,令晓明.基于数学形态学的HSI空间彩色边缘检测方法[J].光电工程,2010,37(4):125 -129.
[8]刘晓,蒋刚毅,吴训威.基于HSL空间的彩色形态变换[J].电路与系统学报,2002,7(1):52 -56.
[9]徐国保,王骥,赵桂艳.基于数学形态学的自适应边缘检测新算法[J].计算机应用,2009,29(4):997 -1002.
[10]杨述斌,彭复员.噪声污染图像中的广义形态边缘检测器[J].计算机工程与应用,2002,38(17):91-92.

