边缘CPF算法及在重力梯度辅助导航中应用
(1. 哈尔滨工程大学 理学院,哈尔滨 150001;2. 哈尔滨工程大学 自动化学院,哈尔滨 150001)
(1. 哈尔滨工程大学 理学院,哈尔滨 150001;2. 哈尔滨工程大学 自动化学院,哈尔滨 150001)
惯导固有原因使得载体长时间航行累积大量误差。可通过重力梯度量测与惯导组合导航方法来修正导航误差。先对重力梯度仪与惯导组合导航原理进行阐述,提出重力梯度仪辅助 INS (GAINS)的系统框架图,对导航用重力梯度图和重力梯度仪进行分析,设定组合量测方程。然后根据状态空间方程的特点,提出使用边缘Cubature粒子滤波(CPF)进行融合估值。通过理论方法证明其对方差的减小,同时给出算法流程。相同条件下与已有APO-PF算法仿真进行经纬度RMSE结果对比,表明该算法估值精度更高;并用CEP对导航误差研究,得到在性能较低的惯导条件下、在梯度仪1E2和10 E2噪声下4h的CEP数值分别为0.044 n mile和0.072 n mile的结果。最后对状态方程简化,定性分析出其余状态量的估值效果。
重力梯度仪辅助惯性导航系统;边缘滤波;状态分解;Cubature粒子滤波;圆误差概率
精确可靠的导航系统是运载器航行关键技术。潜艇长时间水下航行会累积导航误差,而常用的矫正手段GPS信号在水下无法接收,所以需要增加其它的辅助手段。现在有重力/惯性、地形/惯性组合均为研究热点。但理想导航系统工作将是无源的、自动的,不需要发射和接收信号,其中,重力仪和重力梯度仪量测完全是无源的,不易受到外界干扰源干扰,且重力场空间分布特征比较稳定。因此重力和重力梯度辅助导航是水下无源辅助导航的重要方法。
重力辅助导航目前广泛采用的是基于最近等值线点匹配的(ICCP)方法,然而这种方法是在航行一段时间后对状态调整的方法,并且在较大初始误差下就发散[1],即便不发散也常会收敛到局部极小。重力的滤波方法由于重力图在重力变化平缓区域的相似性,经常造成误匹配而误差较大。与重力异常相比,重力梯度能反映重力场(重力加速度矢量)全空间变化率,有5个相互独立的张量。从技术发展角度看,重力量测很难再获得更高分辨率的重力场特征,重力梯度测量则可进一步提高重力场测量的精度和空间分辨率,量测高精度必然使组合导航精度进一步提高。高精度重力梯度图的实现目前在海洋测量领域越来越成熟,逼近程度也越来越精细。
已有重力梯度融合研究较少。非线性滤波方法主要有基于EKF的SITAN算法[2],但该算法在远离真值的位置进行线性化时经常发散;还有使用UKF直接进行非线性传递[3],但UKF使用Sigma样本点数量有限,并不能总是包含真正位置点。近期人工物理优化滤波方法被提出,它采用粒子滤波方法,通过调整在重采样阶段粒子间作用力,改变状态后验分布,克服粒子退化问题,取得了较稳定效果,位置定位误差在140 m左右[4]。虽然误差仍然较大,但说明非线性粒子滤波的可行性。
1 重力梯度辅助导航
重力梯度是重力加速度g的全空间导数,也是重力势的二阶导数[5],单位为厄特弗斯,用E或EU表示,1 E= 1 mGal/10 km。由于重力梯度具有对称性和泊松方程的存在,所以实际上有五个独立的张量Γij(i=x,y,z;j=x,y,z),分别对应不同方向上重力梯度分量。相比于重力异常,它包含了重力场高阶分量,“区别”和“特征”也更明显。已有重力异常滤波辅助导航定位精度不高,在300~500m之间,就是重力异常包含信息量少的缘故。
忽略垂直通道误差,GAINS导航原理说明如下:INS加速度计量测载体想要的加速度里含有重力分量,其中法向分量能够计算补偿,但异常分量无法获取,所以这时的加速度由于加速度计与陀螺仪误差使误差随时间的增长而发散。
重力梯度仪独立于运载器加速度而量测重力场,不含重力仪的厄特弗斯效应,所以其值可用来纠正惯导加速度计输出中异常重力分量。重力梯度仪结合 INS的导航性能相比于传统纯惯导情形有较大幅度提高。但由于惯导和重力梯度仪误差,无图情况下GAINS的东向位置误差仍然会有不断增长的情况。
重力梯度图获得条件下,实现惯导与重力梯度图匹配模式,这种情况下能将实时采集的重力场值和组合系统提供的指示位置在图上得到的计算值做差比较,通过相应滤波算法给出载体实时位置估计,以来限定位置和速度误差。所以图匹配模式是被广泛研究的组合方式[2-4]。
图模式间接反馈的系统框架图如图1所示。

图1 惯导/重力梯度仪导航结构图Fig.1 Configuration for INS/gravity gradiometer navigation
可见 GAINS系统三个重要组成部分为重力梯度数据库、重力梯度仪和数据融合算法。
导航重力梯度库图需事先存储装配到载体上,一般采用离散网格化的形式存储,量值与位置坐标一一对应。当前辅助定位基准梯度图采用实际量测完成的较少,主要是通过理论方法逼近重力梯度。数字高程模型(DEM)正演重力梯度是理论方法逼近重力梯度一种重要形式。DEM主要下载自美国国家地球物理数据中心,它通过假定地面密度常值获得重力场。另外一种是通过自由空间重力异常转化。由于自由空间重力异常包含了周围地形和地下介质共同作用引起的重力梯度,特征更明显。若自由空间重力异常数据分辨率较低时,单独构图反映不了梯度高频特征,这时可与DEM联合构图能取得精细效果[6]。本文所用导航梯度图示例如图3所示。
GAINS的重力梯度仪当前主要使用的是贝尔公司的一种旋转加速度计重力梯度仪。它安装在惯导组件平台上一个缓慢旋转的固定平台装置上,每一个重力梯度仪包含4~8个加速度计,加速度计垂直于旋转轴,其值通过对提取加速度计信号放大处理获取。为了量测5个独立重力梯度分量,需要3个重力梯度仪,单重力梯度仪只能量测重力梯度中的两个分量。
目前国外重力梯度仪有较快的发展和较高的精度。与国外相比,国内部分科研院所从2000年开始对国外重力梯度仪及相关技术跟踪论证和实验研究。但由于技术复杂,从目前已有文献看,国内还不具备制造能实际使用有较高精度重力梯度仪的能力。
融合就是滤波部分。融合算法本文仍然以粒子滤波为基础,根据重力梯度导航系统状态方程线性、量测方程是状态量非线性特点,提出采用边缘Cubature粒子滤波进行状态估计。CKF算法与粒子滤波结合在导航上能使粒子群更快向高似然区移动。
2 边缘Cubature 粒子滤波
2.1 Rao-Blackwell理论
边缘滤波又称Rao-Blackwellised滤波,它是根据统计上的Rao-Blackwell理论[7]。该理论说明统计量在某个函数条件下,通过计算条件均值能提高其估值。它的核心是表示统计量条件和非条件方差之间的关系。具体如下:
对两个变量 U,Y的估计量τ ( U,Y),非条件方差可以表示为条件方差的和:

此公式的理论依据是条件均值性质:

2.2 线性/非线性模型
包括重力梯度导航用一类线性非线性模型为:

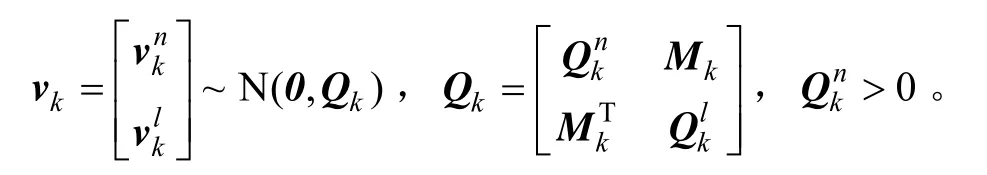




2.3 状态估计过程推导
粒子滤波虽然可以全空间采样而且计算快捷,但会出现样本贫化问题。这里将CKF引入时间更新的重要性采样函数中。CKF是根据Spherical-Radial Cubature准则,通过一组具有相同权重的点结合最新量测,经非线性系统转换后产生新的点给出下一时刻系统状态的预测,其精度可达到三阶[9]。该滤波方法与粒子滤波结合使粒子更快向高似然区移动,在导航应用中得到很高的精度。下面对两种滤波的结合进行推导。

线性状态估值在时间更新阶段为额外的噪声,时间更新分布是:
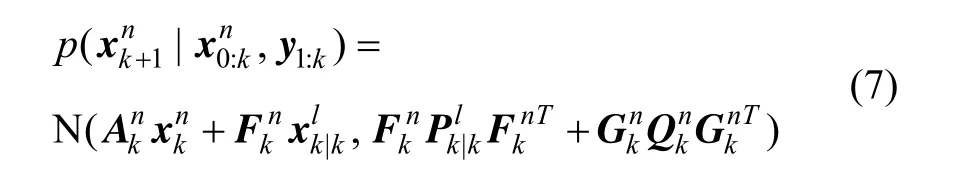
在时间更新阶段引入CKF,CKF作用的模型为:




① 计算Cubature点:


③ 自相关协方差阵:

④ 互相关协方差阵:

⑤ 近似卡尔曼增益:

⑥ 后验均值和协方差:




状态整体后验分布为:
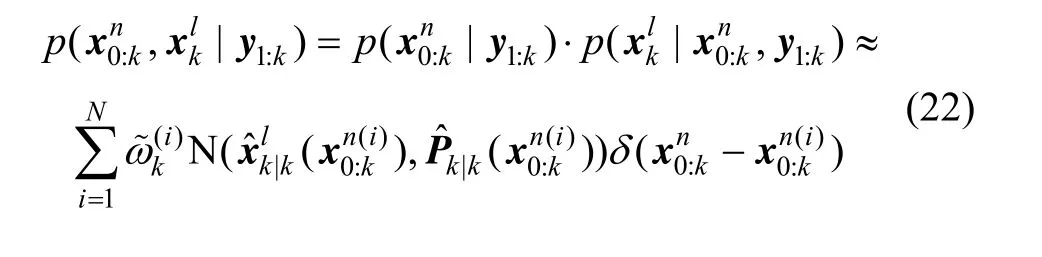
3 边缘CPF重力梯度辅助导航仿真实例
此处惯性导航系统为平台惯导,所用数据为船舶航行实际数据,潜艇潜航一般在24 h以上。这里进行仿真验证,数据时长取7 h,数据采样周期为1 s,并假设梯度图制图精准,不包含图误差。导航器件性能较低,如表1所示。载体轨迹、速度如图2所示。

表1 陀螺和加速度计主要性能参数Tab.1 Parameter of gyro and accelerometer
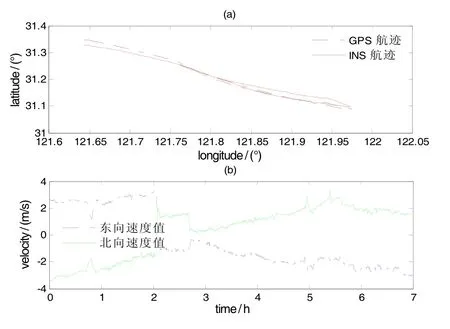
图2 载体轨迹速度图Fig2 Vehicle track and velocity
基准梯度图采用自由空间重力异常正演的重力梯度,分辨率30′。图3列出北向值沿北向分解的 Γxx和东向值沿北向分解的 Γxy两幅。

图3 导航用重力梯度图 Γ xx和 ΓxyFig.3 Gravity gradient map Γ xxand Γxy
重力梯度仪量测值这里采用真实位置的梯度值加上白噪声模拟。
3.1 滤波计算
此处采用平台惯导系统。状态是间接量纬度经度误差(δφ, δλ)、东向北向速度误差(δVx,δVy)、水平方位姿态误差(α,β,γ)、加速度计零位偏差(Δ Ax,Δ Ay)和陀螺常值漂移(εx,εy,εz),系统方程为:

式中,X表示12维状态,状态矩阵A和噪声矩阵G表达式参见文献[4]。系统噪声W为
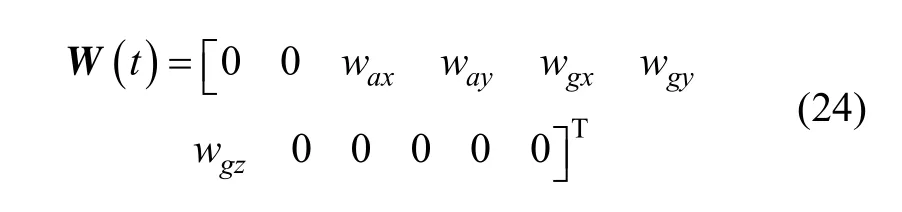
式中, wax、 way、 wgx、 wgy和 wgz均为零均值的高斯白噪声,分别对应加速度计误差和陀螺随机漂移。设滤波周期 Tf=10 s,将状态方程离散化,离散化后表达式:

其中,


由式(28)知,量测方程是状态δL和δλ的非线性函数,而且如果位置误差越小,则梯度之间的差值越小。经纬度误差用粒子集表示,如果粒子能代表位置的真实后验分布,则其对应权值就较大,反之较小。粒子滤波通过递推和更新,可不断估计惯导的位置误差,从而校正系统位置输出。
由于重力梯度数据库以网格形式给出,对于不在网格上坐标梯度值可通过双线性插值获得。海洋中能利用高精度重力梯度仪,噪声可达1Eotvos或更高精度,仿真中设置分量的量测噪声为ij= 10E2。
经纬度误差在量测方程中属于非线性状态,余下误差为线性状态,将状态方程 Ak按照式(3)进行分解:

将状态方程噪声矩阵分解:

滤波时设引入重力梯度辅助定位时的位置误差已达2000 m,仿真粒子数 N= 100,进行10次Monte Carlo仿真,相同条件下滤波稳定后位置均方根误差(RMSE)与APO-PF算法比较结果如图4所示。

图4 纬度经度误差比较Fig.4 Latitude and longitude RMSE comparison
由图4的经纬度RMSE可以看出,MCPF算法经纬度误差估计稳定且始终收敛,其精度高于APO-PF算法。同时MCPF单次运行时间为0.0113 s,高于APO-PF单次的0.418 s。
3.2 结果分析
3.2.1 圆概率误差定位精度分析
常用圆概率误差(CEP)评定导航定位误差,定位误差用到规定点(真实位置或均值)的径向距离表示,这一误差称为圆误差。根据国军标GJB729—1989《惯性导航系统精度评定办法》,船用惯导圆概率误差(CEP)评定试验数据通常以50%置信水平选取概率半径,即R50。它的意义是以真实位置为圆心,包围全部定位误差点一半的圆的半径为 R50,可通过在评定时间内各时刻采样点上位置误差的圆概率误差半径 Rpj中的最大值 Rp来衡量,即 Rp=max Rpj(1 ≤ j≤ m)。若令:

式中,Δ λij、Δ φij表示第i次仿真中第j个时间点的经纬度误差值, xij、 yij、 rij记作水平、垂直、径向位置误差,其中仿真次数 i= 5, j∈[2.7 h, 7 h],每隔10 s进行一次采样。

图5 MCPF 10E2噪声的CEP曲线图Fig.5 CEP curve graph of MCPF under noise of 10E2

图6 MCPF 1E2噪声的CEP曲线图Fig.6 CEP curve graph of MCPF under noise of 1E2
10 E2和1E2梯度仪噪声下4 h航迹CEP曲线如图5和图6所示。表2对1E2和10E2噪声下位置误差进行了比较计算。

表2 算法结果数值Tab.2 Value of algorithm
从表2可见, MCPF算法对所用数据梯度仪1E2噪声比10E2噪声CEP(单位:n mile)[12]及经纬度RMSE都有较大降低。由于使用惯导性能较低,所以当采更高精度的导航仪时,CEP定位精度将会进一步提高。
经纬度以外状态量的估计可通过 MCPF中的Kalman滤波给出。
3.2.2 定性分析
其余状态量估计效果也可通过状态阵简化进行简略定性分析。从图2速度图像可见,载体近似匀速运动,所以东向和北向加速度计值近似为0,即 ▽Ax≈0,▽Ay≈ 0。为明确可观测问题,把短时间内(1~2 min)可忽略不计的元素舍弃以简化系统方程,同时还忽略短时间内地球旋转和地球表面弯曲,≈03×1,≈03×1。简化后,状态转移阵为:

可见,航向失准角γ不可观,因为γ所对应列为零。

载体近似直线航行,因此 - gβ与加速度计偏差▽Ax的和以及gα与 ▽Ay的和是可观测的,即:但可观测性较低,通过载体速度变化可将两者估计出来。水平失准角与水平陀螺漂移耦合,通过转弯,水平失准角与水平陀螺漂移可观测。
陀螺漂移及水平失准角估计图像如图7和图8所示。

图7 陀螺漂移RMSE比较Fig.7 Gyro drifts RMSE comparison

图8 水平失准角RMSE比较Fig.8 Level misalignment angel RMSE comparison
4 结 论
本文使用能更充分利用地球物理场信息的重力梯度辅助惯性导航,对重力梯度辅助导航的基本原理及各部分组成进行了论述。设计了在图匹配下的框架图,并使用新的边缘CPF算法作为融合算法。从理论上证明了边缘粒子滤波能够降低线性状态估计方差。推导了CKF算法与MPF算法结合的MCPF算法流程,给出系统状态方程和量测方程,根据量测是经纬度误差非线性函数特点,状态方程分解。在较大初始误差下,计算表明,MCPF在梯度仪1E2和10E2噪声下,4 h CEP限制在80 m和133 m内。然后通过状态方程简化,对其余状态量估计结果进行了说明。
(References):
[1] 杨勇,王可东,吴镇,等. 不同参数对地形等值线匹配算法精度影响的评估分析[J]. 航空学报,2010,31(5):996-1003.
YANG Yong, WANG Ke-dong, WU Zhen, et al. Evaluation of performance of ICCP algorithm with different parameters[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(5): 996-1003.
[2] Richeson J A. Gravity gradiometer aided inertial navigation within non-GNSS environments[D]. Baltimore: University of Maryland, 2008: 20-32
[3] 王艳东,胡华峰,杨少帅. 重力梯度数据在导航系统中应用[J]. 电光与控制,2013,20(11):11-15.
WANG Yan-dong, HU Hua-feng, YANG Shao-shuai. The application of gravity gradient data to navigation system[J]. Electro Optics and Control., 2013, 20(11): 11-15.
[4] 刘繁明,钱东,刘超华. 一种人工物理优化的粒子滤波算法[J]. 控制与决策,2012,27(8):1145-1156.
LIU Fan-ming, QIAN Dong, LIU Chao-hua. An artificial physics optimized particle filter[J]. Control and Decision, 2012, 27(8): 1145-1156.
[5] Brown D, Mauser L, Young B, et al. Atom interferometric gravity sensor system[C]//2012 IEEE Position Location and Navigation Symposium. 2012: 30-37.
[6] 钱东,刘繁明,李艳,等. 导航用重力梯度基准图构建方法的比较研究[J]. 测绘学报,2011,40(6):736-744.
QIAN Dong, LIU Fan-ming, LI Yan, et al. Comparison of gravity gradient reference map composition for navigation[J]. Acta Geodaetica et cartographica Sinica, 2011, 40(6): 736-744.
[7] Casella G. Rao-Blackwellisation of sampling schemes[J]. Biometrika, 1996, 83(1): 81-94.
[8] Wang Zong-yuan, Sun Feng. Decentralized estimation of nonlinear target tracking based on nonlinear filter[C] //Proceedings of the 2ndInternational Conference on Mechatronic Science, Electric Engineering and Computer. 2013: 22-26.
[9] Arasaratnam I, Haykin S. Cubature Kalman filter[J]. IEEE Transactions on Automatic Control, 2009, 54: 1254-1269.
[10] Affleck C A, Jircitano A. Passive gravity gradiometer navigation system[C]//1990 IEEE Position Location and Navigation Symposium. 1990: 60-66.
[11] Jircitano A, White J, Dosch D. Gravity based navigation of AUV’s. Proceedings of the symposium on autonomous underwater vehicle technology. Washington, 1990: 177-180
[12] 袁赣南,张红伟,袁克非,吴简彤. 基于重力梯度辅助定位的概率神经网络改进方法[J]. 中国惯性技术学报,2013,21(3):369-374.
YUAN Gan-nan, ZHANG Hong-wei, YUAN Ke-fei, WU Jian-tong. Improved probabilistic neural network method based on gravity gradient aided location[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 369-374.
边缘CPF算法及在重力梯度辅助导航中应用
王宗原1,2,孙 枫2
Marginal cubature particle filter and its application in gravity gradient aided navigation
WANG Zong-yuan1,2, SUN Feng2
(1. College of Science, Harbin Engineering University, Harbin 150001, China; 2. College of Automation, Harbin Engineering University, Harbin 150001, China)
INS has large accumulated errors after long journey owing to its inherent reason, which can be decreased by integrating INS with gravity gradient measurement. In this paper, the theory of gravity gradiometer aided INS is described, and its framework chart is presented. Then the gravity map and gradiometer is analyzed, and its measurement equation is set. Based on the feature of state-apace function, a marginal cubature particle filter is proposed to provide estimation in information fusion, and then its variance is proved to be reduced by statistical theory. In addition, the flowchart of algorithm is given, and the simulation is performed. Under the same condition, the position accuracy of the proposed algorithm is higher than that of the existing APO-PF algorithm based on the comparison of their attitude and longitude’s RMSE results. The CEP is used for assessing navigation errors, and it is shown that the gradiometer’s 4 h CEPs under 1E2and 10E2noises are 0.044 n mile and 0.072 n mile, respectively, in low-accuracy inertial navigation system. Finally, the state equation is simplified and used to qualitatively analyze the estimation effect of other state variables.
gradiometer aided inertial navigation system; marginal filter; state decomposition; cubature particle filter; CEP
1005-6734(2014)06-0734-07
10.13695/j.cnki.12-1222/o3.2014.06.007
U666.1
A
2014-07-14;
2014-11-21
中央高校基本科研业务费资助;国家自然科学基金项目(61001154)
王宗原(1977—),男,博士研究生,从事组合导航、非线性滤波研究。E-mail:wangzongyuan@hrbeu.edu.cn
联 系 人:孙枫(1944—),男,教授,博士生导师。E-mail:w0164@sina.com

