自然贮存环境下某型加速度计贮存寿命评估

牛跃听，穆希辉，姜志保，杨振海

（1. 总装备部 军械技术研究所，石家庄 050000；2. 北京工业大学，北京 100022）

自然贮存环境下某型加速度计贮存寿命评估

牛跃听1，穆希辉1，姜志保1，杨振海2

（1. 总装备部 军械技术研究所，石家庄 050000；2. 北京工业大学，北京 100022）

某型加速度计贮存于我国亚湿热、亚干热、温和、干燥4个典型气候区。针对历年统计的加速度计的成败型、不完全故障数据，假设其服从指数分布族、Weibull分布族、极值分布族、对数正态分布族，结合工程实际处理异常数据、“倒挂”数据，采用极小χ2估计对分布函数的参数进行估计，采用极小χ2检验对各分布函数的合理性进行了验证，计算“服从不同自由度下的χ2分布随机变量”检验的拟合优度，得到了加速度计贮存可靠性分布函数。通过统计的故障数据，验证了所提出的数学模型评估方法的适用性和正确性，得到了置信度0.90、可靠度0.95条件下加速度计自然贮存寿命。

加速度计；自然贮存；寿命评估

加速度计是为武器惯导平台提供运动载体加速度信息的关键部件，其显著特点是长期贮存，一次使用。围绕武器系统关键部组件贮存寿命的评估问题是近年来研究热点之一。如果没有长期贮存期间的加速度计检测数据，通常在一些假设前提条件下，采用加速寿命试验的方法，预估其寿命[1-5]。

某型加速度计贮存于我国亚湿热、亚干热、温和、干燥4个典型气候区，至今已经自然贮存接近10年时间，期间积累了大量的检测数据。自然贮存使加速度计受到各种环境因素的综合作用，可以真实、直观地反映其在多环境因素作用下的性能变化规律[6]。那么，加速度计的贮存寿命到底有多长？这是生产和使用单位都十分关注的问题。本文旨在评估加速度计可靠寿命指标，为决策部门提供加速度计订购生产、储备布局、使用维护决策的依据。

1 自然贮存加速度计故障统计

分别抽取自然环境中贮存9年、8年、7年、6年、5年、4年、3年的加速度计样本进行性能检测，检测结果如表1。

在贮存期间加速度计每2年检测一次，检测数据为成败型数据，并且不知道加速度计在检测周期内出现故障的具体时间。因此，加速度计抽样检测数据属于成败型不完全数据。

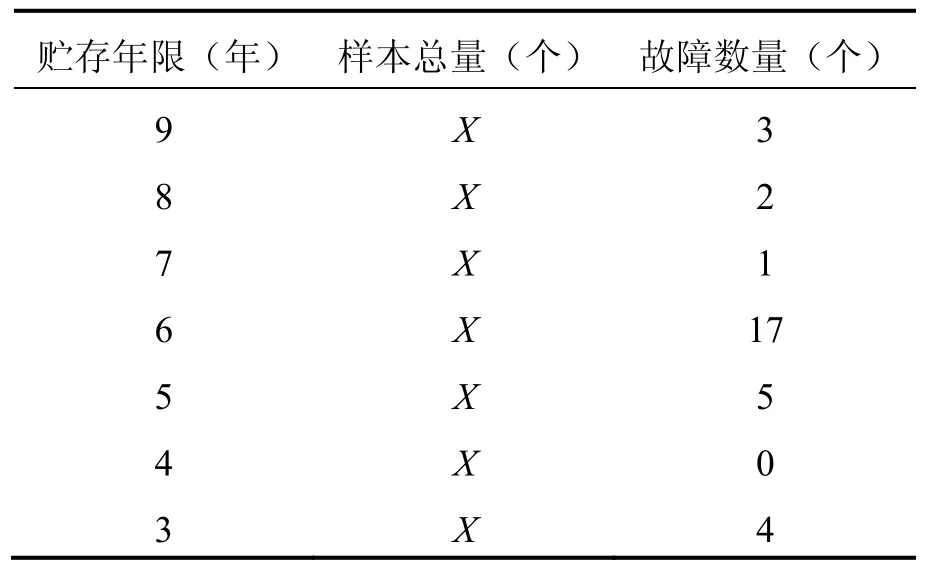
表1 加速度计故障统计表Tab.1 Accelerometer fault statistics

根据加速度计故障统计结果，结合工程实际，运用数理统计的方法评估其自然贮存寿命。

2 贮存可靠性分布函数类型选择及参数确定

为了合理地评估加速度计在自然贮存环境下的贮存寿命，首先需要研究其贮存可靠性的变化规律，确定贮存可靠性分布函数。

下面给出问题的统计模型：

设产品的贮存寿命为X，X的分布函数为F(X,θ)。在时刻ti对X作了ni次观察，其中有Yi次观察值大于或等于ti，ni-Yi次小于ti，但未观察到X的准确值。将X≥ti视为成功，X＜ti视为失败，对连续变量X，观察数据(ni, Yi, ti)是成败型不完全数据，易见：

贮存可靠性分布函数的确定归结为以下两个基本问题：

2.1 分布函数类型的选择

即检验假设H0: F∈p0，p0={F( · ;θ)，θ∈Θ}是分布族，Θ是参数空间。对于贮存可靠性，常见的分布族有指数分布族、威布尔分布族、极值分布族、对数正态分布族等，这一问题称为模型检验。

指数分布族：

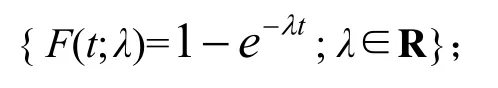
威布尔分布族：

极值分布族：

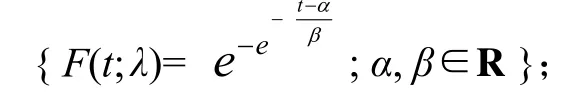
对数正态分布族：

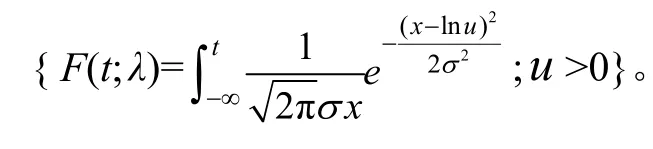
2.2 分布函数中参数的确定

在F∈p0的假设下，基于成败型不完全数据(ni, Yi, ti)，1≤i≤m，估计 F(X, θ)中的未知参数θ。

记时刻ti的第j个样品的贮存寿命为X（iji=1,2,…; j=1,2,…，Xij)独立同分布，其共同的分布函数为F( · ;θ)，θ=(θ1,θ2,…,θs)′∈Θ⊂RS，θ为参数，Θ为参数空间。令：

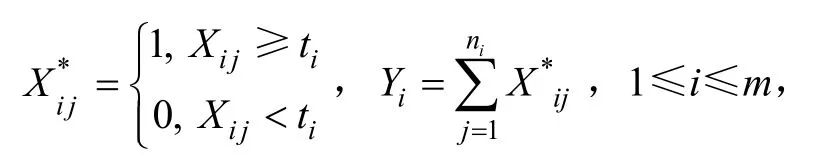
则：Yi～B(ni, Pi)，Pi= Pi(θ)=1-F(ti, θ)，1≤i≤m。

1) 构造χ2统计量

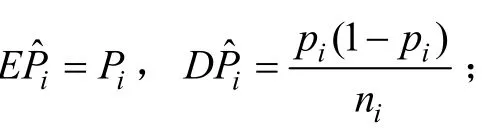
假定贮存寿命X的分布函数F(t, θ)为某一分布族，基于数据(ni, Yi, ti)，1≤i≤m，可以得到在ti时刻：

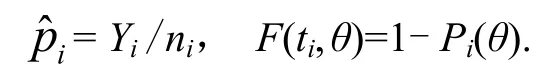
将以上诸式代入式(1)，即可算得χ2统计量。

2) 分布函数中参数的估计

易见，若真实参数为θ0，当ni→ ∞，1≤i≤m，χ2(θ0)渐近于自由度为m的χ2分布。若满足：则称是θ 的极小χ2估计。

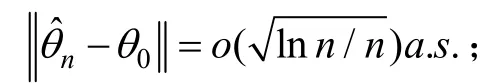
② 当n→∞时，

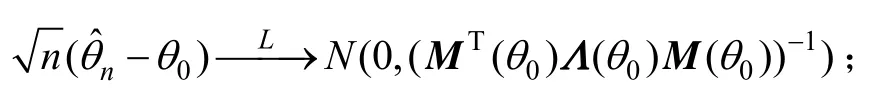
③ χ2()的极限分布（n→∞）为自由度为m-s的分布，其中m是观测样本的次数，s是分布函数中未知参数的个数。

利用上述定理就可以选择较为合适的贮存可靠度分布类型，并对其中的未知参数进行估计。

4) χ2统计量的最小值χ2()及检验

对上述χ2统计量关于θ求最小值，得到极小χ2估计和极小χ2统计量χ2()。利用定理的第三条结论进行极小χ2检验，对于给定的检验水平α，确定拒绝域为：

为明确检验的置信度，可以在作出拒绝或接受原假设的结论的基础上，进一步计算检验的p值。记服从自由度为m-s的分布的χ2随机变量为χ2(m-s)，则：P=P(χ2(m-s)＞χ2())，p为检验的拟合优度，衡量了假定的分布与数据的拟合程度。一般说来，p值越大，拟合程度越好。

对于贮存可靠性中的四种常见分布族：指数分布族、威布尔分布族、极值分布族和对数正态分布族，可以逐一按上述方法进行检验，从中选择一种最为合适的分布类型。

3 贮存寿命评估的理论与方法

记R(t)为某一贮存对象的贮存可靠度，RL为给定的可靠度下限，1-α为置信度，欲求贮存年限T，使得P(R(t)≥RL)=1-α，易见：

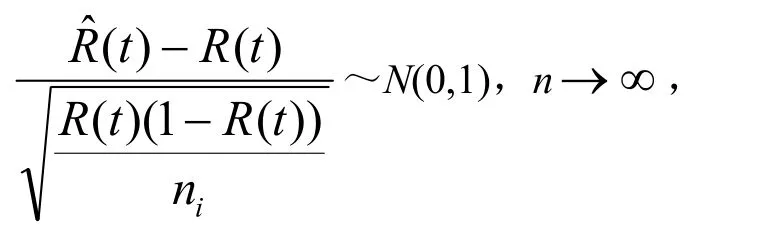
其中，N(0,1)是均值为0，方差为1的标准正态分布。

由于其满足正态分布，则可以推出：

再通过求解不等式可以得到R(t)的下限：

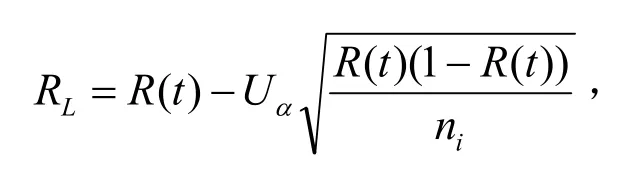
式中，Uα为标准正态分布的 α的上分位数。上面的式子中假定ni全相等。但在本问题中，由于ni不全相等，为了得到较为保守的R(t)下限，可用下式求得：

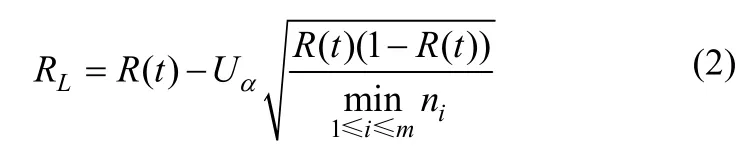
从式(2)中解出R(t)，即可得到所要的T。

4 故障统计数据预处理

4.1 异常的统计数据

分析表1发现：由于抽样误差、检测误差、加速度计批次质量等方面的原因，现有的性能检测数据存在一些问题，主要表现在：

图1 加速度计可靠度分布Fig.1 Accelerometer reliability distribution

为了确定合理的贮存可靠度分布，进而对贮存寿命进行比较可靠的评估，在计算过程中我们针对不同情况对所需的检测数据进行了必要的工程处理。

4.2 异常的统计数据的处理

1）剔除某些异常值。

对于加速度计，个别年份的故障数过高或过低会给分布的选择、确定及寿命预测带来严重影响。对明显的异常数据，能确定产生原因的应予以剔除[7]。

由表1可知：贮存6年的加速度计故障数量为17。通过对贮存 6年的不同批次加速度计故障进行统计（表2）。发现第g、i批次的部件A故障数量明显高于其他批次，说明该批次质量存在问题，处理数据时应剔除该故障数据。同时，也要在贮存6年检测样本总量中去除这两个批次数量（300个）。

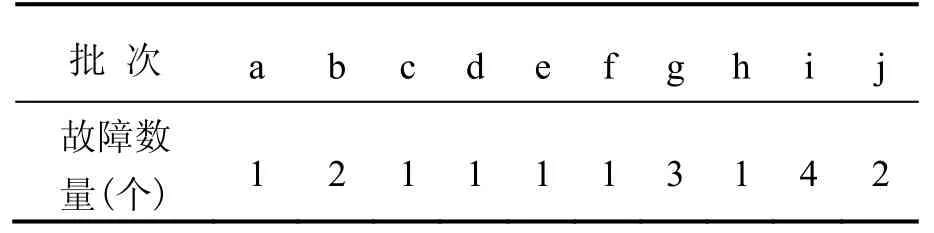
表2 贮存6年的不同批次部件A故障统计表Tab.2 Fault statistics of part A in different batch after storage for 6 years

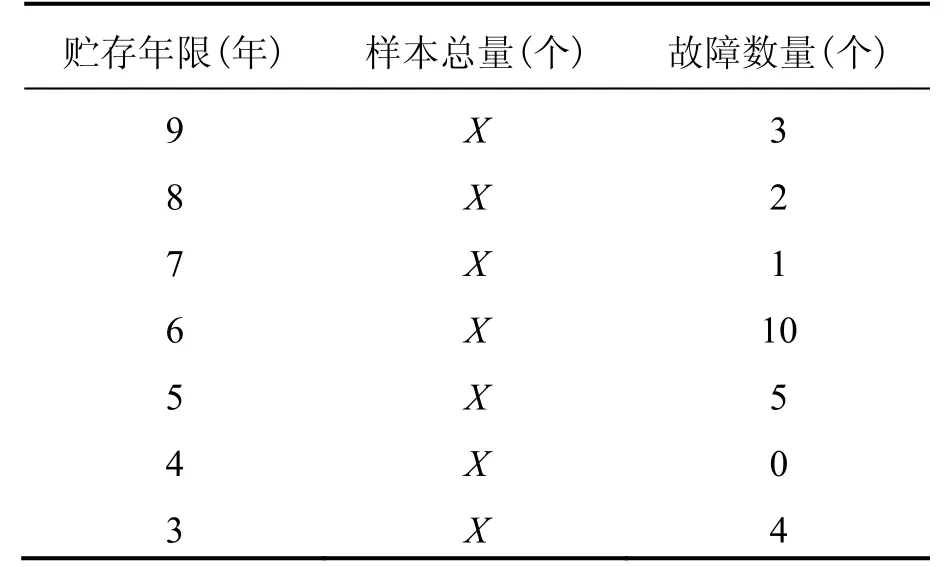
表3 剔除异常值后的加速度计部组件故障统计表Tab.3 Accelerometer fault statistics after eliminating outliers

剔除异常值后的统计表如表3所示。

2）尽量不采用数据倒挂年份数据。

3）基于连续年份的数据进行计算。

在计算过程中还遵循了这样的原则：尽量使用连续几个年份的数据，以减少由于外推产生的误差。

5 计算结果

各假设分布类型、假设检验、拟合优度、贮存寿命评估结果如表4所示。比较表4计算结果可知：极值分布的χ2统计量中，0.2569最小，p值最高，并且极小χ2检验结果为接收，所以判定加速度计符合极值分布。取置信度 1-α=0.90，RL=0.95，利用式(1)算得加速度计的贮存寿命为12.94年。

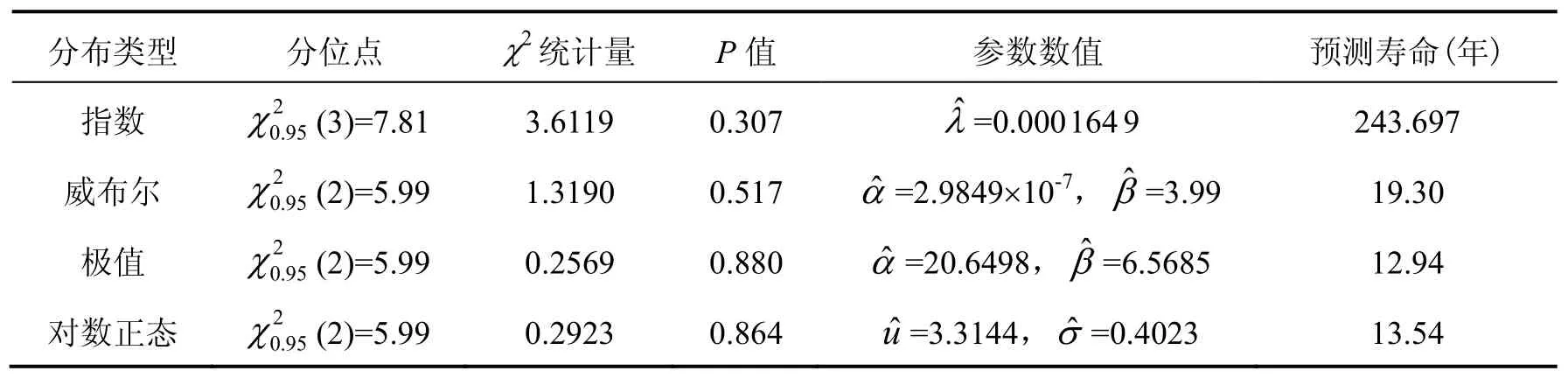
表4 加速度计备选分布类型相关计算情况Tab.4 Related calculation situations of accelerometer’s alternative distribution types

6 验证与评价

我们从以下几个方面进行了分析和考察，以验证和评价计算结果的合理性。

6.1 拟合优度评价

在应用极小χ2检验选择贮存可靠度分布类型时，计算了检验的p值，即拟合优度[8-9]，其p值在0.3065至0.880之间，拟合得比较好[10]。

6.2 可靠度分布函数计算与年度统计数据可靠度比较

利用确定的分布函数对各年份的可靠度进行了预测，与检测数据得到的可靠度估计进行了比较。

以贮存3年的加速度计为例，其年度统计数据可靠度为：

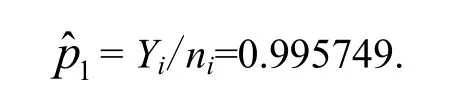
加速度计服从极值分布，由其可靠度分布函数计算得到贮存3年时的可靠度为：

极值分布族：

两者的相对误差为：

同理，可求得加速度计的年度统计数据可靠度、可靠度分布函数年度可靠度，以及两者相对误差，见表5。可见两者相对误差较小，预测精度较高。

表5 加速度计各年份可靠度预测值与估计值的比较Tab.5 Comparison of accelerometer reliability between the predicted values and the estimated value each year

（References）：

[1] 袁宏杰，李楼德，段刚，吴浩. 加速度计贮存寿命与可靠性的步进应力加速退化试验评估方法[J]. 中国惯性技术学报，2012，20(1)：113-116.

YUAN Hong-jie, LI Lou-de, DUAN Gang, WU Hao. Storage life and reliability evaluation of accelerometer by step stress accelerated degradation testing[J]. Journal of Chinese Inertial Technology, 2012, 20(1): 113-116.

[2] Lee Jinsuk, Pan Rong. Analyzing step-stress accelerated life testing data using generalized linear models[J]. IIE Transactions, 2010, 42(8): 589-598.

[3] Bae S J, Kim S-J, Park J I, et al. Lifetime prediction through accelerated degradation testing of membrane electrode assemblies in direct methanol fuel cells[J]. International Journal of Hydrogen Energy, 2010, 35: 9166-9167.

[4] Wohlgemuth J H, Kurtz S. Using accelerated testing to predict module reliability[C]//IEEE Photovoltaic Specialists Conference, 2011: 3601-3605.

[5] LI Xiao-yang, JIANG Tong-min. Optimal design for stepstress accelerated degradation with competing failure modes [C]//Annual Reliability and Maintainability Symposium, 2009: 64-68.

[6] 杨振海，安保社. 基于成败型不完全数据的参数估计[J].应用概率统计，1994, 10(2): 142-147. YANG Zhen-hai, AN Bo-she. Parameter Estimation Based on Binary Date[J]. Chinese Journal of Applied Probabi1ity and Statistics, 1994, 10(2): 142-147.

[7] 李东阳. 弹药储存可靠性分析设计与试验评估[M].北京：国防工业出版社，2013. LI Dong-yang. Ammunition storage reliability analysis design and test assessment[J]. Beijing: Defense Industry Press, 2013.

[8] Su Y, Shi H F. Goodness-of-fit analysis for uniformity in a bounded solid region[C]//Proceeding of the Ninth International Conference on Machine Learning and Cybernetics, 2010(1): 231-235.

[9] ZHAG Feng, GAO Yuan-Ning, HUO Lei. A viable method for goodness-of-fit test in maximum likeihood fit[J]. Chinese Physics C, 2011, 35(6): 580-584.

[10] 杨振海，程维虎，张军舰. 拟合优度检验[M]. 北京：科学出版社，2011.

Storage life assessment of an accelerometer under natural storage environment

NIU Yue-ting1, MU Xi-hui1, JIANG Zhi-bao1, YANG Zhen-hai2
(1. General Armament Ordnance Technology Institute, Shijiazhuang 050000, China; 2. Beijing University of Technology, Beijing 100022, China)

In our country, a certain type of accelerometer is stored in four typical climate zones which are sub humid, Asia hot, mild and dry zones. In view of the historical statistics (accelerometer's success or failure, and incomplete failure data), assuming that they are subject to exponential distribution, Weibull distribution, extreme value distribution and logarithmic normal distribution, and by combining with the engineering data to handle the exceptions and "upside down" data, a minimum χ2estimation method is used to estimate the parameters of the distribution function, and the fit goodness of “obey distributed random variables under different degrees of freedom χ2” test is calculated. In this way the storage reliability distribution function of an accelerometer is obtained. The fault data statistics verify the applicability and validity of the proposed mathematical model assessment method, and the accelerometer natural storage life is obtained under the condition of confidence 0.90 and reliability 0.95.

accelerometer; natural storage; life evaluation

1005-6734(2014)04-0552-05

10.13695/j.cnki.12-1222/o3.2014.04.024

TJ760.6

A

2014-04-18；

2014-07-28

中国博士后科学基金资助项目（2013M532181）

牛跃听（1978—），男，博士后，主要研究方向为信息化弹药寿命评估与延寿技术。E-mail：nyt369@sina.com