基于学生行为分析的兴趣课程推荐系统的研究

袁文翠，于文娟，赵建民

0 引言

网络教学方兴未艾，各大高校也纷纷推出自己网络教学平台，但大多数都只是给予学生被动接受式教育，没有充分从学生个人角度出发考虑学生的兴趣、需求及认知风格,造成了交互性差,学习效率低等问题。本文从学生个人角度出发，通过对学生行为特征的调查分析，评估其兴趣课程并对具有相同兴趣的学生聚类，为其提供个性化课程推荐服务，从而建立个性化课程推荐系统，为学生选课做出参考。本系统的构建有助于提高学生的学习效率，避免耗费过多时间寻找课程，实现自主学习，因材施教。

通过查阅文献，主要有以下研究与本文相关：文献1基于协同过滤技术对相关课程的评分进行聚类,以此为基础根据学生对相似课程的评分高低预测学生的兴趣课程。这种方法的缺点在于只根据课程评分单方面的数据推断学生兴趣度过于片面，而且很多用户对自己的兴趣课程也不一定很明确，特别是当课程领域较复杂时，即使用户愿意提供评分,也不一定是准确的[1]。文献2提出一种隐式的用户兴趣度获取方法。该方法用多元线性回归模型来计算用户对某网页的兴趣度 ,以用户浏览时间和拉动滚动条次数作为主要影响因素，较准确地计算了用户对网页的兴趣度[2][3]。本文将以学生为主体，分析其行为特征，运用聚类分析和线性回归模型，将兴趣课程相似的学生聚类到同一个学生群中，并找出其中的关联性，最终完成兴趣课程的推荐[4]。

1 学生行为分析与过程

学生行为信息可分为两大类，第一类为可以直接获取的静态信息，由学习者通过信息注册或填写问卷调查来完成，这是最直接的获得学生兴趣和需求的方式，但缺点是依赖于学生的主动提供，而学生通常不注意或不愿意花时间去认真填写，这在很大程度上降低了可用性。第二类为间接获取的动态信息，包括学生的学习历史、学习时间或出勤率、考试成绩等，这些信息可通过现有的教务系统直接获取。另外，我们将学生划分为新用户和老用户，老用户有自己的修课记录，通过访问学生行为信息数据库，可以得到学生的动态信息，如选课记录、出勤率、考试成绩等，将这些信息进行处理和挖掘，便可提供个性化课程推荐；新用户没有动态行为信息，因此，必须依据学生填写的静态数据，测评其兴趣课程，从而给予推荐服务。

基于学生行为分析的个性化课程推荐系统分为 3个步骤，如图1所示：

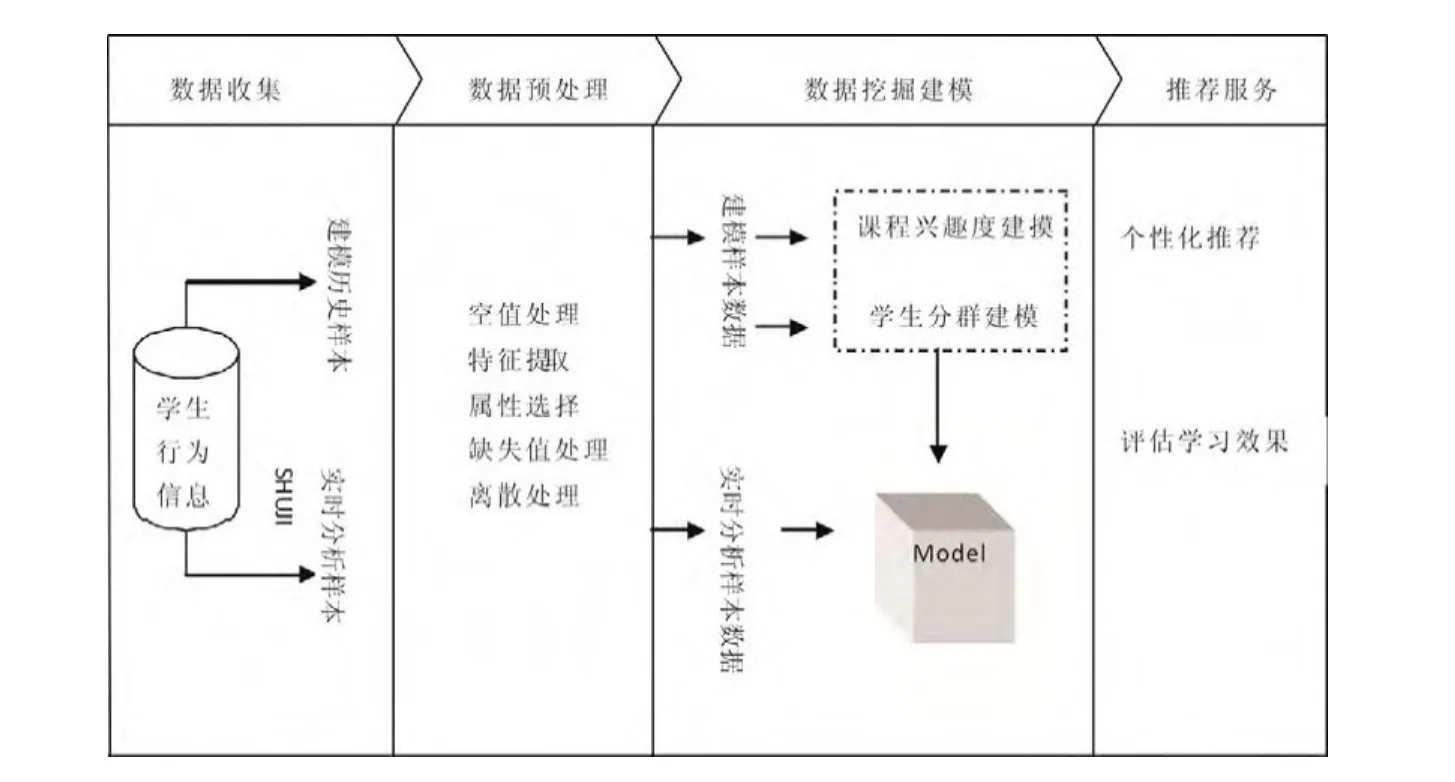
图1 兴趣课程推荐流程

（1）数据收集与预处理

当学习者注册成为用户时,系统会从已有教务系统中获取与该学习者相关的信息，并存入学生行为信息库。这些信息包括选课记录、出勤率、考试成绩，以及系统自身提供的静态信息。对于注册过程中可能出现的数据项空缺、数据类型不一致等问题，需要进行有效的数据预处理，预处理包括转换整合、抽样、随机化、缺失值处理等。

（2）数据挖掘建模

为了确定向目标学习者推荐哪些课程，首先，要确定学生对选修课程的兴趣度模型，兴趣度模型通过分析前面处理后的学生动态信息和静态信息，利用多元线性回归方程建立。其次，需要建立学生分群模型，分群模型是通过上一步计算得到的不同课程的兴趣度，结合 K-means聚类分析算法，确定学生群模型。

（3）个性化推荐服务

两个学生属于同一个簇（学生群）表明他们感兴趣的课程是相似的，但某学生选修了某门课程并通过学习后，对该课程的评价也可能会非常低，而另一个学生可能恰恰相反。因此，还需要将评价信息进行反馈更新，预测目标学习者对候选课程集合中每门课程的评价，取评价值高、兴趣度高的课程推荐给学生。

2 兴趣课程的推荐

学生学习过程中的心理活动与其表现出的行为密切相关，心理活动在某一层面上可以理解为课程兴趣度；学生在学习时的各种行为特征同样决定了课程兴趣度，这些相关因素之间存在某种线性关系，为了量化兴趣度，本文建立多元线性回归模型，计算课程兴趣度，并采用K-means聚类分析算法构建学生群细分模型实现个性化课程推荐功能。

2.1 课程兴趣度的建模

从直观看，能够揭示用户对课程的兴趣度的行为有很多，为了找到学生行为信息与课程兴趣度之间的定量关系，本文查阅了大量文献，发现起关键作用的是两种行为：选修课出勤率和考试成绩，最终将多元线性回归的方法应用到获取学生对课程的兴趣度中[6]。设I(P)（课程兴趣度）是与t(P)（某选修课出勤率）、o(P)（某选修课考试成绩）有关的随机变量，方程如公式（1）所示：

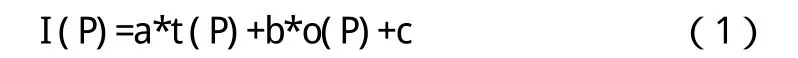
其中，a、b、c都是与t(P)和o(P)无关的未知参数，服从正态分布，a和b称为回归系数（本文称a、b、c为学生行为影响因子），通过代入具体的行为参数值与兴趣值求出。对一组样本点用最小二乘法得到一线性回归方程（1），但它未必有意义。当且仅当 I(P)与 t(P)、o(P)之间的确存在线性相关关系时，回归方程才有意义，因此必须对回归方程和回归系数分别进行显著性检验，只有得到有效性验证后，才可将其用作课程兴趣度的量化估算公式。根据收集到的用户数据，利用最小二乘法求得 a=0.1112，b=0.0056，c=0.0794，r=0.9440，其中r为相关系数，r越接近于1说明相对误差越接近于0，线性回归的效果也就越显著。为了检验该模型的正确性，再随机选择其他10个学生，处理他们的行为特征数据，利用求得的方程计算他们对某课程的兴趣度，与预测的课程兴趣度作比较,分析结果如图2所示：

图2 课程兴趣度

从图2中可以看出，计算出的课程兴趣度结果与预估课程兴趣度的结果非常接近,计算可得两者的比值有60%在0.9以上，最低的也可达到69.57%，平均值达到88.11%，这说明了通过回归模型计算得到的学生课程兴趣度与预估的课程兴趣度比较一致，同时验证了采用回归模型来计算学生对选修课程兴趣度的合理性及准确性。

2.2 学生的分群建模

学生群细分是根据学生对每一门课程的兴趣度将学生划分成为同类群体的过程。细分的目的是按照学生之间的密切关系或相似程度划分到各个学生群中。这里我们将课程兴趣度作为样本数据，采用K-means聚类[5]分析的算法将具有相同爱好的学生分到同一学生群中，实现思路是：

给定一个数据集D（包含n个学生对每一门课程的兴趣度，兴趣度的值由前面的兴趣度模型算出），把D中的n个对象（学生）分配到k个簇（学生群）中，使得评分函数E在此划分下取值最小，即该评分函数E是以簇内学生感兴趣课程高相似性，和簇间学生感兴趣课程低相似性为目标,定义为公式（2）：

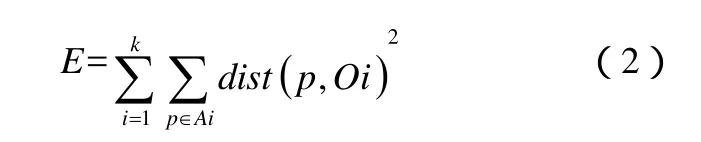
其中，E是数据集中所有对象（学生）的误差的平方和；p是空间中的点（代表某个特定学生）表示给定的数据对象；Oi是第i个簇的中心点（任意选择k个学生）。对于每个簇中的每个对象，求对象到簇中心点距离的平方，然后求和。算法流程如下：

从n个学生样本中，任意选择k个对象作为初始的簇的中心点k-center；

利用公式（2）计算数据集D中的每个学生 p 到 k 个中心点学生的距离；

（3）把每个学生 p分配到距离他最近的中心点所属的簇中；

（4）重新计算选取每个簇（学生群）的中心点；

（5）重复（1）（2）（3）步骤遍历完所有对象之后，直到算法收敛，即平方误差最小。

根据得出的学生群分类就可以对目标学生的兴趣课程进行预测，生成推荐结果。通常根据推荐目的不同，可以进行多种形式的课程推荐。基于学生行为分析的个性化课程推荐系统可以说是从学生个人的角度来进行相应推荐的，而且是自动的，即学生获得的推荐是系统从学生行为信息隐式获得的，不需要用户努力地去找到自己感兴趣的推荐信息。

3 实验验证

本文采用MATLAB统计工具包对学生课程推荐的准确性进行验证，我们随机抽取42名学生对11门选修课程的兴趣度作为实验数据集，根据课程的关联性将簇（代表学生群个数）分为4类，运用k-means算法构建学生群细分模型。

当聚类准确率达到最高 0.8333时，可以得出聚类结果如表1所示：

表1 聚类结果

学生群1对CAD、flash动画制作、计算机维护课程比较感兴趣，对其他课程关注一般。

学生群2对卫生学、养生学课程比较感兴趣，对其他课程不太关注。

学生群3对哲学、心理学课程比较感兴趣，对其他课程不太关注。

学生群4对篮球、排球、网球课程比较感兴趣，对其他课程不太关注，如表2所示：

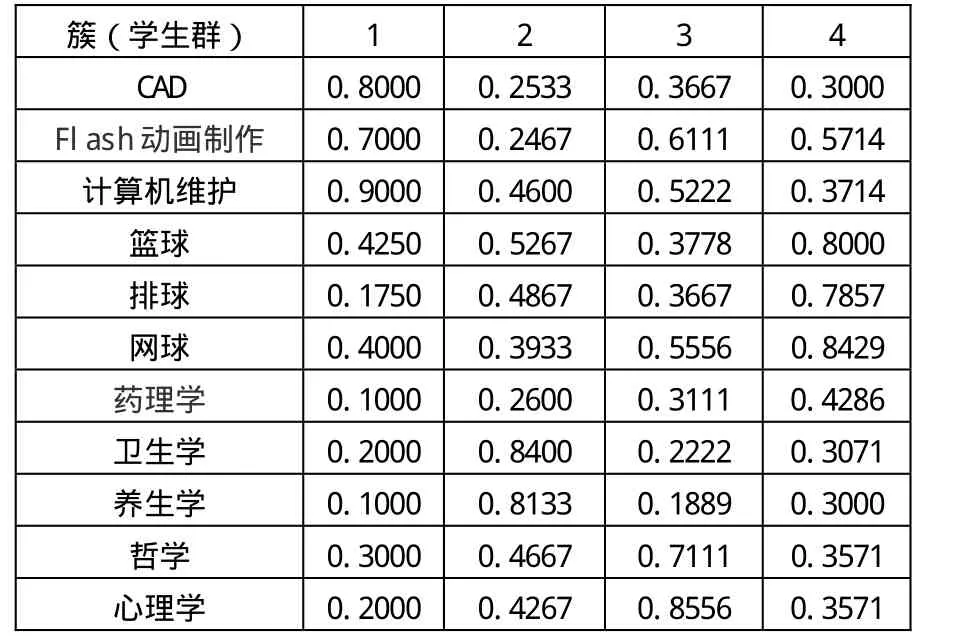
表2 簇中心学生对课程的兴趣度

4 总结

本文提出了一种基于线性回归模型和聚类分析算法的兴趣课程推荐方法，首次将数据挖掘技术和线性回归模型相结合引入到兴趣课程推荐中来。实验证明，该方法可以为学生准确地提供课程推荐服务，有效提高学生学习效率，减少了学生选课的盲目性。本研究的特色：（1）为学生建立一个课程推荐机制，让学生不用再凭主观臆想随便选课，本系统的建立希望可以为学生最优选课做参考；（2）将学生个人的出勤率和考试成绩等行为信息作为学生最优选课推荐的依据；（3）将多元线性回归模型和聚类分析算法相结合，将具有相同兴趣爱好的学生聚集到同一群中，从而有效的区别对待不同学生，达到最优化配置学习资源的目的。

在未来研究中可加入更多的课程、兴趣课程推理算法以及评价反馈策略使系统更加完善，从而提供全方位的课程推荐服务；也可以在学校教务系统中挂接此系统，为学生选课提供有效的参考。

[1]周丽娟,徐明升,张研研,张璋.基于协同过滤的课程推荐模型[J].计算机应用研究,2010,27(4):1316-1318

[2]付关友,朱征宇.个性化服务中基于行为分析的用户兴趣建模[J].计算机工程与科学, 2005, 27(12): 76-78.

[3]赵银春,付关友,朱征宇.基于 Web浏览内容和行为相结合的用户兴趣挖掘[J].计算机工程,2005, 31(12): 93-108.

[4]郝兴伟,苏雪 E-learning中的个性化服务研宄[J]山东大学学报理学版2005, 40(2) ：67-71

[5]MacQueenJ.Some Methods for Classification and Analysis of Multivariate Observations [C].In: Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability.Berkeley，University of California Press，1967: 281-297.

[6]刘兆兴，张宁，李季明.基于协同过滤和网络结构的个性化推荐算法[J].复杂系统与复杂性科学，2011，8（2）：45-50.