应力阴影效应对水平井压裂的影响
才 博 唐邦忠 丁云宏 杨振周 何春明 唐术华 陈春霞
1.中国石油勘探开发研究院 2.中国石油勘探开发研究院廊坊分院 3.中国石油华北油田公司4.中国石油吐哈油田公司温米采油厂 5.中国石油吐哈油田公司鄯善采油厂
近年来,国内外非常规领域水平井及体积压裂技术的进步与规模应用,使非常规油气资源得以高效经济开发并发挥出革命性作用[1-2]。但在水平井压裂设计中,裂缝间距及分簇间距这一影响产量、采收率和经济效益的重要因素仍尚不清楚,其核心在于水力裂缝产生的应力阴影效应(stress shadow)的表征与计算仍不明朗。自20世纪80年代,Warpinski和Teufel已开始研究平行裂缝之间的相互作用,并给出开启一条恒定裂缝高度、有限裂缝长度的裂缝后,裂缝周围产生应力场的解析解[3];2004年 Fisher和2006年 Mayethofer在微地震的矿场研究中证实这一现象;2009年Olson得出这一效应的一个明显作用效果是在多条平行裂缝中,中间的裂缝的裂缝宽度最小,这是因为两边的裂缝对中间的裂缝都产生压缩应力[4]。2010年Bunger等在研究Barnett页岩气时进一步证实这种效应的存在,并将这种效应称为应力阴影效应[5];2011年Roussel和Sharma指出水平井改造中,一定裂缝间距内前一条支撑裂缝会导致下一条裂缝附近的应力转向,在下一相邻段裂缝中出现与主缝向切的裂缝系统[6]。国内学者赵金洲等也在研究我国页岩气压裂设计中,指出压裂在单一裂缝脆弱面上将产生诱导应力,并指出产生应力阴影的诱导应力可以改变最大与最小主应力的分布,使裂缝发生转向[7]。前人多数研究集中在静态条件下的两条平行裂缝间的相互作用上,对多段多条裂缝下如何表征应力阴影及其影响因素仍是有待解决的问题,研究也进一步证实应力阴影效应及其影响因素是合理设计并利用人工裂缝最大限度发挥裂缝作用和效果的重要科学问题。因此,笔者在上述前人研究的基础上进行了深入研究。
1 应力阴影效应
随着工具设备及水平井改造技术的不断进步,储层多段改造的规模、段数等越来越多[8-9]。水力压裂设计师可利用分簇射孔将分段改造距离设置得越来越近,但往往过多的分簇与分段未必就带来理想的效果,Roussel认为应力阴影效应的产生机理主要在于支撑剂的填充导致人工裂缝附近引起了应力场的变化,蒋廷学等也在研究我国页岩气压裂设计中指出,压裂在单一裂缝脆弱面上产生诱导应力的存在,并指出产生应力阴影的诱导应力可以改变最大与最小主应力的分布,使裂缝发生转向[10]。上述研究表明,应力阴影效应可引起人工裂缝从水平井的横切缝中开始偏离朝向或远离以前的裂缝方向延伸,使得下一裂缝发生转向。Barnett页岩裂缝间距30m时水平井压裂裂缝产生的应力阴影效应如图1-a所示,可见从第二条裂缝开始裂缝出现了与主缝向切的裂缝系统,而Eagle Ford页岩压裂的裂缝监测情况,同样是30m的裂缝间距没有出现裂缝应力阴影效应(图1-b)。因此研究阴影效应的产生机理,建立分析数学模型并进行其影响因素分析对水平井分段体积改造优化设计及效果的提升具有重要研究与应用价值。

图1 同等裂缝间距、不同储层条件下裂缝延伸示意图
2 数学模型
2.1 假设条件
假定流体流动满足应力—渗流耦合连续性方程、运动方程和状态方程[11]。裂缝的扩展与延伸模型复合经典的Perkins、Kern和Norgren(PKN)与Khristianovic、Geertsma和Dekerk(KGD)理论模型,具体假设条件为:①油气藏为均质无限大且各向同性;②流动流体为牛顿流体;③不考虑地层温度对裂缝内流体的影响;④暂不考虑裂缝系统内启动压力的影响;⑤岩石破裂满足摩尔库伦屈服准则;⑥岩石的变形为弹性变形,不考虑岩石蠕变。
2.2 单缝应力场模型
为能合理有效研究多条裂缝间应力阴影效应引起的诱导应力变化情况,首先建立以单一裂缝为主的均质,各向同性,弹性和有界的三维裂缝模型(图2),在此基础上,利用应力叠加原理进行多条裂缝模型研究。假设岩石上下隔层的杨氏模量和泊松比为Eb、vb,生产层油层的杨氏模量和泊松比为Eb、vp,裂缝高度并没有失控(即hf<hp),裂缝的闭合压力可以利用净压力和最小水平应力计算得到。即

因此对于单一裂缝,可通过上述方程计算裂缝诱导应力大小计算。

图2 裂缝示意图
2.3 多缝应力场模型
基于第1条裂缝应力分析基础,对下一条形成的裂缝进行应力分析,由于应力阴影效应,第2条裂缝净压力的模型为:

则第n条裂缝内的净压力为:

因此,上述力学模型中对第n条缝的应力阴影效应为前面裂缝的综合诱导应力叠加,只需要求得前面的综合诱导应力就可以得到n条缝内的净压力。
2.4 应力阴影求解
考虑裂缝平面上的应力变化,假设二维人工垂直裂缝(图3)。
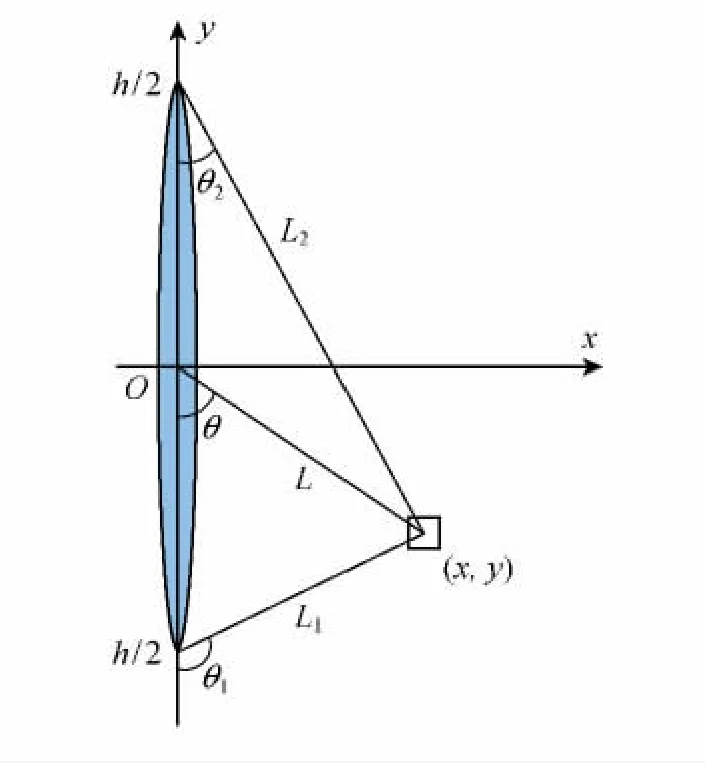
图3 二维垂直裂缝示意图
则在水平面上人工裂缝所引起的不同位置的诱导应力为:


由广义Hook定律计算得:

同时,各几何参数间存在以下关系:

利用式(1)~(6)可计算裂缝诱导应力大小,上述研究表明在地层最小水平主应力不变的情况下,诱导应力大小与裂缝内的净压力具有直接关系,应力阴影诱导应力对裂缝网络扩展形态的影响具有双重作用。首先,在压力和宽度叠加的过程中,由于应力阴影的影响,附加的正应力改变每个裂缝单元原始的就地应力值,这直接影响裂缝内压力和宽度的分布,导致裂缝的扩展发生改变。其次,考虑应力阴影诱导应力(正应力和剪应力)后,裂缝扩展端部的局部应力场发生改变,可引起局部主应力方向发生改变。局部主应力方向发生改变又会引起裂缝发生转向,进一步影响裂缝网络扩展形态。因此,研究应力阴影影响因素指导压裂设计显得尤为重要。
3 影响因素分析
以某口致密储层x水平井为例,水平段长度1 043 m,储层有效孔隙度8%,有效渗透率0.12mD,地层孔隙压力29.0MPa,杨氏模量25 000MPa,泊松比0.2,最小水平主应力43.2MPa,抗张强度3.5MPa。分段改造设计6~10段。利用上述数学模型计算水平井10段改造下不同段内的净压力及裂缝形态表明:100 m的段间距内裂缝将发生转向(图4、5)。
3.1 杨氏模量和泊松比

图4 水平井10段改造各段内裂缝净压力图

图5 水平井10段改造裂缝形态图
为进一步研究储层岩石力学参数对应力阴影的影响,设置不同泊松比和杨氏模量进行研究。考察泊松0.2、0.35、0.45比时,结果表明泊松比对应力阴影的影响较小,即便在泊松比为0.5的极端情况下,导致的净压力变化幅度仍不大,因此产生的应力影响很小(图6)。考察杨氏模量20 000MPa、25 000MPa、30 000 MPa等3种情况,研究表明:杨氏模量对裂缝内净压力值的变化影响较大,产生的应力阴影现象越强烈,杨氏模量越高对裂缝应力阴影效果影响也较大(图7)。因此,储层岩石力学参数中杨氏模量对应力阴影现象的影响最敏感。

图6 不同泊松比下缝内净压力变化特征图
3.2 水平主应力差
在给定储层条件下变化水平主应力差值,考察水平主应力差值1MPa、3MPa、6MPa等3种条件对应力阴影的影响。结果表明:随着应力差的增大净压力值变小,所形成的应力阴影效应也逐级变小,储层应力差的越小,形成的诱导应力范围越大,对邻近段裂缝改造的阴影效应越大,导致裂缝间的相互作用越强,促使裂缝发生转向,形成复杂裂缝网络。

图7 不同杨氏模量下缝内净压力变化特征图
3.3 施工排量与砂比
考察同等施工规模条件下,施工排量对应力阴影效应的影响程度,施工排量在5~12m3/min变化时,结果表明随着排量的增大净压力增大,所形成的应力阴影效应的也显著增加,因此施工排量对应力阴影效应的影响敏感性强,同样的研究表明施工砂比对应力阴影效应的影响敏感性较弱。
3.4 分段间距的影响
在水平井单段同等规模、同等施工参数条件下,考察水平井裂缝间距为100m、125m、200m等3种不同分段裂缝间距下对应力阴影效应的影响。结果表明:在同等条件下,随着裂缝间距的增大,形成的应力阴影效应显著变小,对邻段的改造裂缝的阴影效应减小,利于裂缝长度的延伸但不利于复杂裂缝网络的形成,但过近的裂缝间距可使得缝内诱导应力过大,对施工安全不利。
4 矿场试验
在上述优化研究的基础上,利用文中模型及研究结论,对本井进行分段设计与工艺参数优化,按照设计参数对本井进行现场6段大型压裂改造施工,注入总液量4 480m3、加砂320m3。微地震监测结果表明:利用人工裂缝应力阴影效应进行分段改造后,人工裂缝出现多处转向裂缝,说明利用应力阴影效应实现了6段压裂下最优改造体积,较以往未考虑应力阴影下节约3~4段改造井段,降低成本30%以上,为水平井多段的体积改造优化提供重要技术指导。
5 结论
笔者借鉴Bunger提出的应力场分析假设条件,从水平井单一横切缝入手,建立考虑应力阴影的应力场叠加数学模型并推出数学公式,在此基础上得出简化的水平井多段应力阴影效应应力场模型。影响因素分析表明:储层地质参数中杨氏模量,水平主应力差对应力阴影效应的影响大,而泊松比对应力阴影效应的影响几乎很小;施工参数中施工排量对应力阴影效应的影响明显,在一定储层条件下,分段及簇间距越小,应力阴影效果对水平井裂缝附近其他裂缝的扩展产生应力阴影影响越大。
利用文中研究结果对致密层水平井进行优化设计与现场施工。微地震表明结果:利用应力阴影效应只压裂6段就实现了以往10段压裂的改造体积,较以往未考虑应力阴影下节约3~4段,降低30%以上成本,对合理利用应力阴影效应进行水平井体积改造裂缝尺寸设置及工艺参数优化具有重要指导意义。
符 号 说 明
pnet为裂缝内净压力,MPa;pc为裂缝内压力,MPa;σhmin为最小水平主压力,MPa;σf为岩石抗张强度,MPa;σy诱导为人工裂缝引起的诱导应力,MPa;wo为裂缝缝宽;Ep为油层的杨氏模量,MPa;vp为储层的泊松比;hf为裂缝高度,m;p2net为第2条裂缝内净压力,MPa;σ1y诱导为第1条裂缝引起的诱导应力,MPa;pnnet为第n条裂缝内净压力,MPa;i为变量;C为裂缝半缝高度,m;x为缝长方向距离,m;y为缝宽方向距离,m;如θ、θ1和θ2为负,则用θ+180°、θ1+180°和θ2+180°代替。
[1] 赵政璋,杜金虎.致密油气[M].北京:石油工业出版社,2012.ZHAO Zhengzhang,DU Jinhu.Tight oil and gas[M].Beijing:Petroleum Industry Press,2012.
[2] 贾承造,张永峰,赵霞.中国天然气工业发展前景与挑战[J].天然气工业,2014,34(2):1-11.JIA Chengzao,ZHANG Yongfeng,ZHAO Xia.Prospects of and challenges to natural gas industry development in China[J].Natural Gas Industry,2014,34(2):1-11.
[3] 潘林华,张士诚,程礼军,等.水平井“多段分簇”压裂簇间干扰的数值模拟[J].天然气工业,2014,34(1):74-79.PAN Linhua,ZHANG Shicheng,CHENG Lijun,et al.A numerical simulation of the inter-cluster interference in multi-cluster staged fracking for horizontal wells[J].Natural Gas Industry,2014,34(1):74-79.
[4] OISON J E,DAHI T A.Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures[C]∥paper 119739presented at the SPE Hydraulic Fracturing Technology Conference,19-21January 2009,Woodlands,Texas,USA.New York:SPE,2009.
[5] BUNGER A P,ZHANG X,JEFFREY R G.Parameters affecting the interaction among closely spaced hydraulic fractures[C]∥paper 140426presented at the SPE Hydraulic Fracturing Technology Conference,24-26January 2011,the Woodlands,Texas,USA.New York:SPE,2011.
[6] ROUSSEL N P,SHARMA M M.Strategies to minimize frac spacing and stimulate natural fractures in horizontal completions[C]∥paper 146104presented at the SPE Annual Technical Conference and Exhibition,30October -2 November 2011,Denver,Colorado,USA.New York:SPE,2011.
[7] 赵金洲,任岚,胡永全.页岩储层压裂缝成网延伸的受控因素分析[J].西南石油大学学报:自然科学版,2013,35(1):1-7.ZHAO Jinzhou,REN Lan,HU Yongquan.Controlling factors of hydraulic fractures extending into network in shale formations[J].Journal of Southwest Petroleum University:Science & Technology Edition,2013,35(1):1-7.
[8] 曾凡辉,郭建春,刘恒,等.北美页岩气高效压裂经验及对中国的启示[J].西南石油大学学报:自然科学版,2013,35(6):90-98.ZENG Fanhui,GUO Jianchun,LIU Heng,et al.Experience of efficient fracturing of shale gas in North America and enlightenment to China[J].Journal of Southwest Petroleum University:Science & Technology Edition,2013,35(6):90-98.
[9] 张涛,郭建春,刘伟.清水压裂中支撑剂输送沉降行为的CFD模拟[J].西南石油大学学报:自然科学版,2014,36(1):74-82.ZHANG Tao,GUO Jianchun,LIU Wei.CFD Simulation of proppant transportation and settling in water fracture treatments[J].Journal of Southwest Petroleum University:Science & Technology Edition,2014,36(1):74-82.
[10] 蒋廷学,贾长贵,王海涛,等.页岩气网络压裂设计方法研究[J].石油钻探技术,2011,39(3):36-40.JIANG Tingxue,JIA Changgui,WANG Haitao,et al.Study on network fracturing design method in shale gas[J].Petroleum Drilling Techniques,2011,39(3):36-40.
[11] 叶源新,刘光廷.岩石渗流应力耦合特性研究[J].岩石力学与工程学报,2005,24(14):2518-2523.YE Yuanxin,LIU Guangting.Research on coupling characteristics of fluid flow and stress within rock[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(14):2518-2523.

