一种改进对称波束的低仰角闭环跟踪算法

李涛护，高保生

(中国电子科技集团公司第五十四研究所，河北石家庄 050081)

0 引言

采用阵列天线能够进行同时跟踪处理多个空间信号，具有良好的应用前景。无线电测控系统跟踪低仰角目标时，由于地形环境反射、折射产生的多路径效应，会引起接收信号在幅度和相位上的变化，导致跟踪目标的精度降低，甚至导致跟踪目标丢失，因此，需要解决阵列天线的低仰角跟踪问题［1，2］。

如何减少多路径效应对低角目标跟踪性能的影响，目前主要有降低旁瓣、分集、数据引导和单轴跟踪等方法［3－5］，但这些技术都是在某些特定环境下使用的，阵列天线一般使用空域滤波技术降低多路径效应的影响。文献［6，7］研究了通过控制天线波束的照射方向，使低仰角跟踪目标的仰角与镜像目标的仰角关于波束中心对称，然后再利用和差波束的对称性，抵消掉多路径信号的影响。这种方法能够有效抑制镜面反射引起的多径影响，但也存在明显的局限性。首先需要估计出波束中心的指向角，然后要求目标和镜像同时处于和波束的照射范围内，应用范围较窄。本文根据在相邻脉冲内低仰角目标运动特征基本保持不变的事实，提出了一种利用连续的脉冲轮流指向目标和镜像以实现对称波束的改进方法，该方法有效突破了照射波束对角度的限制，能够在更大仰角范围内抑制多径的影响，具有良好的应用价值。

1 镜面反射多径效应模型

多径反射包括镜面反射和漫反射两部分。在平坦地面或者平静海面上以镜面反射为主，镜面反射信号与直射信号具有较强的相关性，其信号相位随目标位置的改变呈现出有规律的变化;在城市、山区等地势起伏较大的环境中以漫反射为主，漫反射信号是由各点散射形成的反射信号，信号相位呈现明显的随机性。由于漫反射和地形因素密切相关，难以建立典型的模型，为了方便研究，本文假设工作环境为平坦地面环境，即只考虑镜面反射。

镜面反射的几何模型［8，9］如图1所示，A表示天线中心高度，B表示目标高度，接收机接收来自目标仰角θt的直射信号，同时接收镜像从反射角θi进入的反射信号，γ表示天线波束中心指向与水平面的夹角。

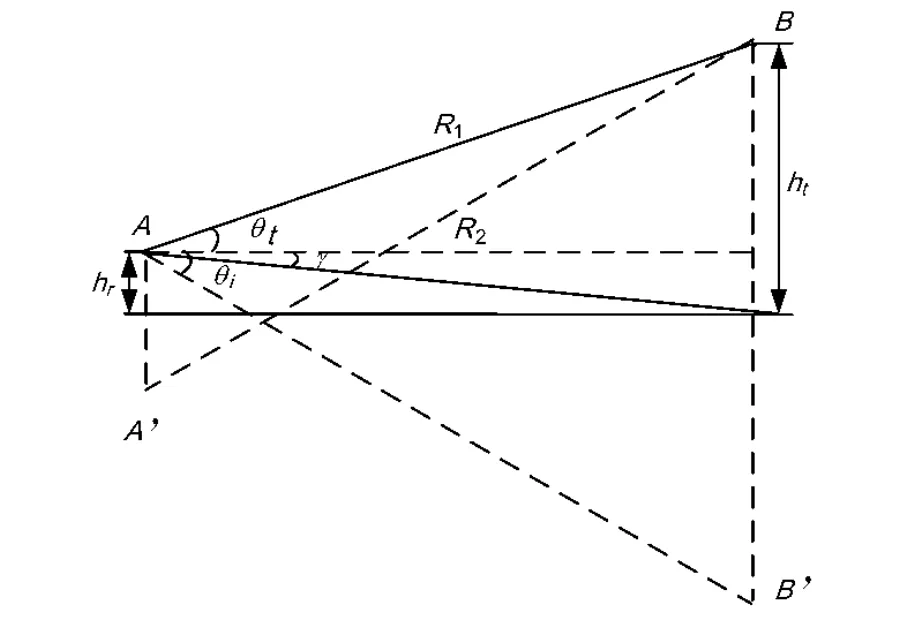
图1 镜面反射几何模型

2 低仰角多径消除算法

2.1 对称波束法消除多径原理

单脉冲体制利用天线的和、差方向图函数对目标进行跟踪测量。在不存在多径信号时，设ε表示目标相对于天线波束中心的偏转角，和波束电压增益为 FΣ(ε)，差波束电压为 FΔ(ε)，经过跟踪接收机的信号接收后产生误差控制电压驱动，天线向差方向图为零的方向运动实现对目标的跟踪。

在低仰角或负仰角条件下，天线接收包括来自目标的直射波和经各种地形反射的反射波。假设只考虑镜面反射的影响，当阵列天线的波束中心指向水平角时，系统的和信号强度和差通道信号强度分别为［10］:

式中，ES为天线方向图与输出信号强度间的比例因子;θt为天线仰角;θi为地面反射角;ρ为地面反射的模，其值在0～1之间变化;φ为接收点处直射波与反射波的相位差:

式中，Φ0为反射波相角;δ0为直射信号和反射信号路径差。

当天线波束中心指向目标与镜像之间夹角的角平分线时，目标仰角和镜像仰角大小相等，方向相反，即关于波束中心对称。令θ0=θt+γ表示相对于波束中心的目标仰角，则θi－γ=－θ0表示镜像仰角。此时，式(1)、式(2)可改写为:

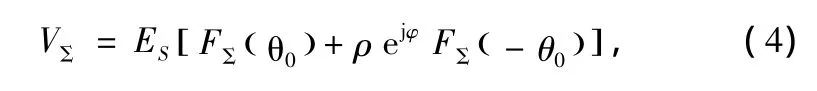
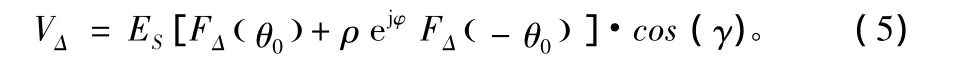
式中，γ根据不同波束指向在0和π之间取值。

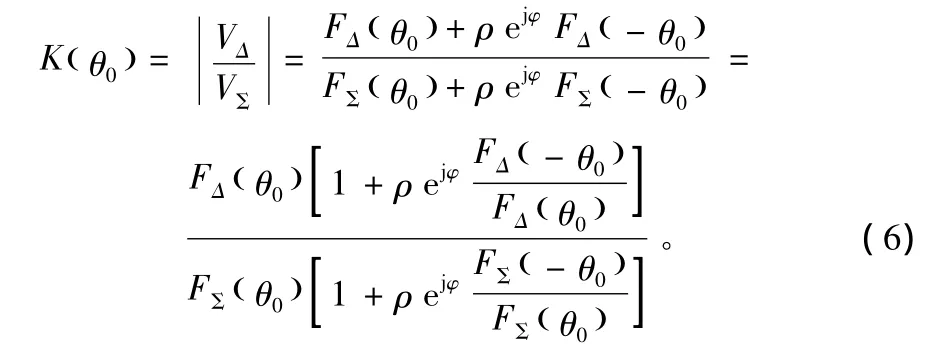
当波束方向图的幅度满足对波束中心偶对称时，有

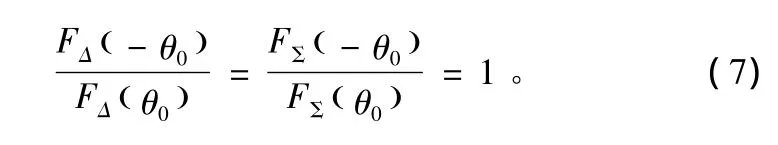
此时从式(6)可以得出:

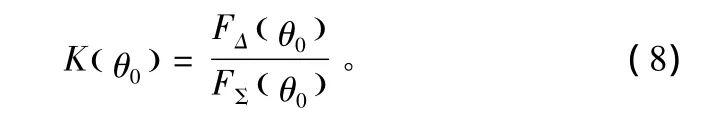
式(8)表明，当天线波束中心指向目标与镜像的角平分线时，即差波束与和波束方向图之比满足偶对称条件时，对称波束法可消除多径干扰，提高系统抗多径能力。

2.2 对称波束法性能分析

对称波束法的应用前提是需要目标和镜像同时处于和波束的照射范围内。为了提高对称波束法的适用范围，往往需要展宽波束主瓣，但宽主瓣波束会带来几个问题:①降低跟踪精度;② 会增加来自地平线附近的漫反射分量和随机误差;③是降低了波束的角度分辨率，当跟踪波束无法区分目标和镜像时，此时将难以消除多径影响。

下面根据仿真说明了镜面反射多径对对称和差波束跟踪性能的影响。均匀线阵波束阵元数为32，接收天线中心高度为5 m，目标飞行高度为300 m，水平距离从2～20 km，和差波束分别用Taylor加权和Bayliss加权，旁瓣抑制度为30 dB，从图2中可以看出，当镜像仰角为3°左右时，跟踪波束已不具备区分目标和镜像所需的角度分辨率，多径信号引起了较大的跟踪误差，且随着目标仰角的降低，这种不利影响逐渐加大，跟踪误差表现出逐渐扩大的趋势。

图2 多径效应对对称波束跟踪性能的影响

3 改进对称波束的闭环跟踪算法

单脉冲跟踪系统利用天线和差波束方向图函数测出目标方向。当目标和镜像之间夹角很小时，若和差波束不具有能区分该夹角的角分辨能力，就会引起较大的跟踪误差，甚至导致跟踪系统不可用。但从镜面反射多径效应模型可以看出，目标和镜像具有比较明确的几何关系，因此可以根据该特点通过误差补偿，消除多径的影响。

3.1 相邻脉冲差波束跳变实现对称波束

在单脉冲体制跟踪系统中，相邻脉冲内目标运动特征基本保持不变，在不改变和差波束工作模式的前提下，使相邻的差波束指向每次均跳变180°，在2个相邻脉冲内实现对称波束，其原理图如图3所示。

图3 相邻脉冲差波束跳变法原理

在不存在多径信号的情况下，差波束的对称中心直接指向直射信号，保持跟踪误差为零。当在脉冲1中多径信号从 －θi方向进入差波束方向图，若经过一个脉冲时间后多径信号基本维持不变，则在脉冲2中差波束进行了相位跳变，使得此时多径信号的仰角变为+θi，从而通过补偿消除该方向多径的影响。

容易看出，改进的对称波束法不再要求目标和镜像同时处于和波束的照射范围内，有效突破了照射波束对角度的限制。

3.2 改进对称波束的闭环跟踪算法

闭环跟踪指天线波束连续跟踪目标，利用角误差信号控制天线波束对目标的随动。根据单脉冲跟踪体制的原理，每个脉冲输出一次角误差信号。差波束跳变补偿的本质是将目标和镜像之间的几何关系引入，并对跟踪结果进行误差补偿。

设闭环跟踪的第k个脉冲时测得的目标仰角为θtk，则根据图一给出的目标和镜像之间的几何关系，容易推出镜像目标的仰角为θik，并令跟踪误差为ek，由于相邻脉冲之间信号特征保持不变，不考虑ES的影响，则k+1个脉冲各分量可以表示为:

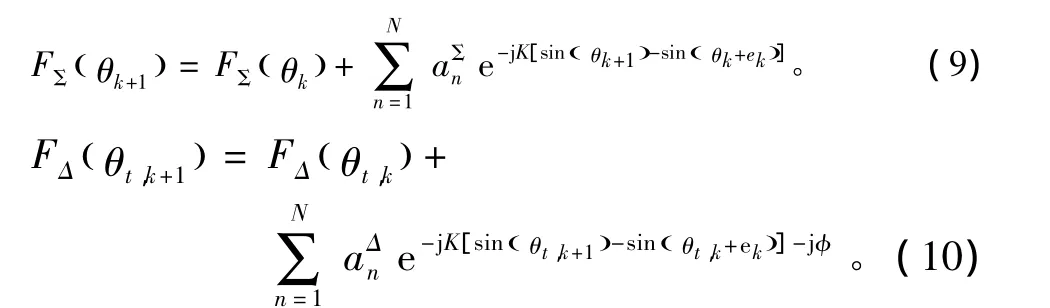
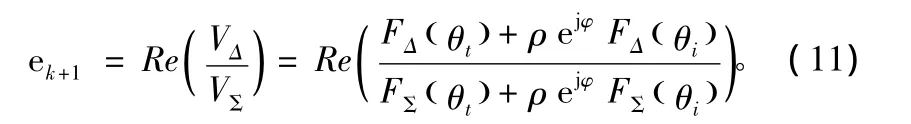
3.3 开环跟踪误差对闭环性能的影响

闭环跟踪法的实质是波束中心瞄准线指向目标仰角和镜面反射角的角平分线、使差波束保持对称的稳态过程，当跟踪正常状态，闭环跟踪误差趋向于零值。当在跟踪初始阶段，或者跟踪过程中出现了信号中断导致不能进行正常的闭环运行，瞄准线必须保持在某一预先确定的角度上或程序给定的角度上，则此时可利用式(8)推断出误差信号，闭环跟踪算法将引导环路重新收敛。图4给出了初始时刻开环误差分别为5°和2°时闭环跟踪环路的收敛过程。

其中测角误差为:

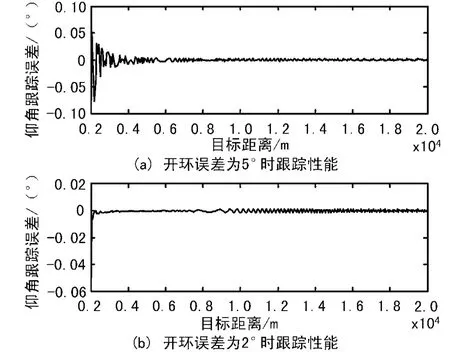
图4 存在开环误差时闭环跟踪性能

可以看出，算法有比较明显的收敛过程，且随着开环误差的降低，收敛过程明显加快。

3.4 算法性能分析

仍采用2.2节的仿真参数对改进对称波束的闭环跟踪算法进行了性能分析。跟踪误差如图5所示。

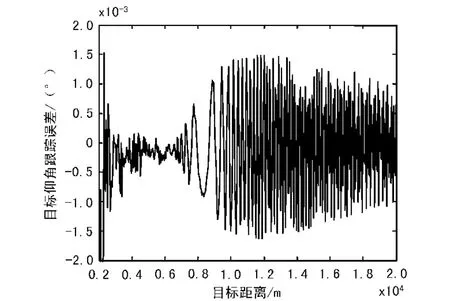
图5 改进对称波束的闭环跟踪性能

容易看出，采用了改进对称波束的闭环跟踪算法后，因波束角分辨能力不足引起跟踪误差得到了明显抑制，且跟踪性能并没有因为目标仰角降低而恶化，具有较强的适应性。

4 结束语

简要分析了对称波束在低仰角环境下的性能和局限，提出了利用2个连续波束构造对称波束的新思想，给出了闭环跟踪算法，并通过了仿真结果验证了算法性能。 ■

［1］王英玲.低仰角跟踪技术研究及应用［J］.无线电工程，2008，38(2):44 －47.

［2］张永泰.多径效应与低仰角跟踪［J］.遥控遥测，2000，21(2):26－32.

［3］朱庆和.克服多路径效应的自适应偏轴跟踪方法［J］.火力与指挥控制，2000，25(4):20 －23.

［4］杨世海，胡卫东，万建伟，等.多径反射下低空目标检测研究［J］.电子与信息学报，2002，24(4):492－498.

［5］DAEIPOUR E，BLAIR W D.Bias Compensation and Tracking with Monopulse Radars in the Presence of Multipath［C］∥Aerospace and Electronic Systems，IEEE Trans，1997:863 －882.

［6］BARTON D K.Low-angle Radar Tracking［J］.Proc.IEEE，1974，62(6):687 －704.

［7］刘建华.DMC雷达低空目标探测与仰角测量方法研究［D］.长沙:国防科技大学研究生院，2001.

［8］BAR S Y，KUMAR A.Tracking Low Elevation Targets in the Presence of Multipath Propagation［J］.IEEE Trans.on AES，1994，3(30):973 －979.

［9］WANG Xi-qing，PENG Ying-ning，MA Zhan-ge.An Algorithm Based on Elevation for Geometric Mean for Monopulse Radars to Track a Target at Low Altitude［J］.CIE Inter.Confer，1996(10):739 －742.

［10］SEBT M A.SHEIKHI A.Nayebi.Robust Low-angle Tracking by Beamforming［C］∥Radar Conference，2009 IET International，2009:1－6.