临海既有混凝土氯离子侵蚀及钢筋初锈时间预测

张俊芝， 庄华夏， 伍亚玲， 刘如泰

（浙江工业大学 建筑工程学院，浙江 杭州 310014）

随着服役期的不断延长，海洋环境下的混凝土结构存在的耐久性问题会越来越严重.沿海混凝土结构的耐久性问题主要表现为氯盐侵蚀引起的钢筋锈蚀［1－2］.然而，临海混凝土结构不仅承受氯盐侵蚀，还受潮水冲刷和荷载作用等其他因素的影响，室内试验一般很难模拟这些自然环境因素共同作用下的氯离子侵蚀过程［3］.因此，研究临海既有混凝土结构氯离子侵蚀特征，分析其实际抗侵蚀性能，是自然环境下混凝土结构耐久性研究的重要手段之一.

本文以浙江省温州市瓯江口的既有混凝土水闸闸墩为背景工程，取得该水闸闸墩混凝土芯样，对闸墩混凝土的配合比进行了推定，测试了芯样中不同深度处的自由氯离子浓度；根据实测的混凝土中自由氯离子浓度，分析了该水闸混凝土中氯离子侵蚀的规律，并对该水闸闸墩混凝土的氯离子扩散性能、钢筋初锈的临界氯离子浓度和钢筋初锈时间等抗氯离子侵蚀性能进行了分析.

1 既有临海水闸工程及混凝土

1.1 既有水闸工程概况

本文研究的既有水闸处于浙江省温州市龙湾区瓯江口的自然环境下，距离河流入海口约1km.该水闸建成于1998年4月，之后投入运行.水闸为1孔，净宽5.0m，钢闸门；设计过流流量为50.2m3／s，闸底板高程（吴淞高程）1.48m.在服役15a后，水闸左右两侧有一定的沉降.

1.2 混凝土芯样

结合该水闸的加固改造，2012年12月18日取得该水闸闸墩混凝土芯样.该水闸直接拦挡潮水，退潮时内河水位排泄至下游，两翼墙混凝土冲蚀严重.内河水质受到污染，在氯离子等侵蚀介质作用下，钢闸门及翼墙混凝土腐蚀严重，闸门槽混凝土有冲蚀及钢筋锈胀裂缝，裂缝最大宽度不大于1.0mm，如图1.

图1 既有水闸闸墩混凝土的冲蚀Fig.1 Erosion of concrete of existing sluice pier

取样位置均在闸墩下部，以闸门槽为界，上、下游各取5个芯样；高度距离闸底板77～180cm，具体取样位置见图2.混凝土芯样直径6cm，长度为10～20cm不等.

图2 既有水闸闸墩混凝土芯样的取样位置Fig.2 Concrete cores'location of existing sluice pier（size：mm）

1.3 既有混凝土配合比

既有混凝土的历史性能是耐久性研究的依据，其配合比是室内模拟试验的基础.根据该水闸的施工竣工验收资料，此水闸闸墩混凝土的配合比为：mC∶mW∶mS∶mG＝1.00∶0.53∶2.00∶3.88.

本文参考文献［4］的方法，对所取得的闸墩混凝土水灰比进行了推定.根据推定结果，上游3号芯样2组混凝土的配合比分别为：mC∶mW＝1.00∶0.57，mC∶mW＝1.00∶0.53.下游4号芯样2组混凝土的配合比分别为：mC∶mW＝1.00∶0.54，mC∶mW＝1.00∶0.57.取4组芯样的平均值，则该水闸闸墩混凝土的水灰比为0.55.施工竣工验收时的水灰比为0.53，两者较为接近，推定结果能较好地反映既有混凝土原有的水灰比，说明文献［4］的推定方法对既有混凝土水灰比的推定是可行的.

2 既有混凝土氯离子侵蚀特性

2.1 闸墩混凝土中氯离子浓度分布

将取得的混凝土芯样用HDM－150混凝土研磨机，按2mm厚度的规格逐次从其表面一侧向内侧研磨，所得粉末过0.63mm筛，直至距混凝土外表面以下30mm时结束.每个芯样取得15个深度处的粉末.将这些粉末置于烘箱内烘2h，取出冷却至室温待用.混凝土中自由氯离子浓度1）本文中的氯离子浓度均指其占混凝土质量的百分数.利用美国THERMO Orion DUAL Star PH／离子浓度测量仪测定［5］.

由于取芯位置接近，以取得的上、下游芯样对应深度处氯离子浓度的平均值作为该环境因素下闸门槽上游与下游混凝土中的氯离子浓度样本值.测得混凝土中的自由氯离子浓度分布如图3所示.

图3 闸门上、下游混凝土中的自由氯离子浓度与深度关系Fig.3 Free chloride ion concentration in concrete vs.depths

分析图3可知，在闸门槽上、下游两种含氯环境下，闸墩表面混凝土均存在明显的氯离子对流区，上游混凝土氯离子对流区厚度为26mm，下游混凝土氯离子对流区厚度为24mm.上述情况说明，氯离子对表面混凝土的主要侵入方式是对流作用而不是扩散作用.在24～26mm以后，混凝土中自由氯离子浓度呈明显的下降趋势，氯离子的侵入以扩散方式为主.另外，下游混凝土中的自由氯离子浓度总体上比上游混凝土中高，主要原因是下游环境水体中的氯离子浓度比上游高.

2.2 临海既有混凝土的氯离子扩散系数

众多研究表明，氯离子在既有混凝土内部的扩散符合Fick第二定律，则该水闸闸墩混凝土氯离子浓度可用扩散方程表示为［6］：

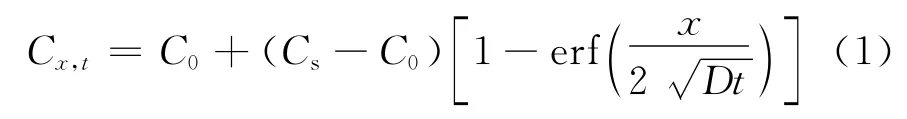
从该水闸建成运行到取芯样时共计运行5 350d（14年零8个月），方程（1）中的侵蚀时间t＝5 350×24×3 600＝4.622 4×108s.再根据测得的自由氯离子浓度，用上述方程以最小二乘法拟合既有混凝土中的氯离子扩散系数，即将每个混凝土芯样在不同深度处的坐标值（xi，Cxi，t）代入方程（1）.由于氯离子在混凝土表面并不符合扩散规律，故排除对流区数据，以稳定扩散区的最高氯离子浓度处作为扩散表面，要求相关系数R2尽可能接近1作为拟合优度的检验，拟合以下方程：

式中：C1为对流区与扩散区界面处的自由氯离子浓度，%；X1为对流区厚度，mm.

用图3中的氯离子浓度数据可拟合得到：上游混凝土 D＝1.985×10－13m2／s，相关系数 R2＝0.992；下游混凝土D＝2.515×10－13m2／s，相关系数R2＝0.972.这与文献［6］中同样侵蚀时间下混凝土中氯离子扩散系数的数量级吻合，其结果是可信的.从计算结果来看，下游混凝土中的氯离子扩散系数较上游稍大，其差异主要在于下游混凝土所处环境的氯离子浓度比上游大，且取芯的位置比上游要高，此处水位变化频繁，干燥时间较长.

3 临海既有闸墩混凝土钢筋的初锈时间预测

3.1 混凝土钢筋初锈时间预测的 Monte Carlo方法

利用排除对流区氯离子浓度值的扩散参数，则以氯离子扩散系数为常数的钢筋初锈时间可以从氯离子扩散自对流区与扩散区的界面开始来进行预测［6－7］.对式（2）进行变换，可得到钢筋初锈时间的预测表达式为：

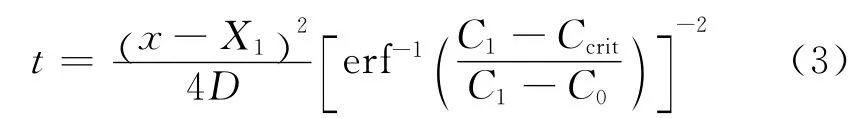
式中：t为钢筋初锈时间，d；Ccrit为钢筋初锈的临界氯离子浓度，%.

3.2 既有水闸闸墩混凝土钢筋锈蚀预测

根据所取闸墩混凝土芯样，测得钢筋保护层厚度均值为35mm，钢筋的初锈时间即为钢筋表面达到临界氯离子浓度的时间.对上、下游各5个芯样的对流区厚度取平均值，得到上游X1＝23.6mm，下游X1＝22.0mm.经调查，此水闸施工时以当地自来水为混凝土拌和用水，故认为C0＝0.

分别以0.18%，0.12%和0.06%为临界氯离子浓度均值，取标准差均为0.02%［8］，将上述扩散参数及其统计分布（均为正态分布，但有研究认为除混凝土保护层厚度为正态分布外，其余变量为对数正态分 布［8］），利 用 式 （3）即 Monte Carlo 法 模 拟10 000次，求得闸墩上游混凝土中钢筋初锈时间分别为3 513，3 440，964d（即35mm处的氯离子浓度达到临界浓度的时间）.临界氯离子浓度均值不同时，上游混凝土中钢筋初锈时间概率密度如图4所示.运用同样的方法对下游5个芯样进行分析，模拟10 000次得出闸墩下游混凝土钢筋初锈时间分别为3 382，2 710，1 017d.临界氯离子浓度均值不同时，下游混凝土中钢筋初锈时间概率密度如图5所示.

图4 上游混凝土中钢筋初锈时间的概率密度Fig.4 Probability density of the initial corrosion time of steel bar in upstream concrete

图5 下游混凝土中钢筋初锈时间的概率密度Fig.5 Probability density of the initial corrosion time of steel bar in downstream concrete

从上述模拟结果得知，当临界氯离子浓度均值为0.12%～0.18%时，混凝土中钢筋初锈时间约为3 000d；当临界氯离子浓度均值为0.06%时，钢筋初锈时间只有1 000d左右.该水闸从1998年建成服役5 350d后，闸门及翼墙混凝土腐蚀较严重，混凝土中有钢筋锈胀裂缝.采用0.12%～0.18%为钢筋锈蚀的临界氯离子浓度所预测的钢筋初锈时间，与实际情况是较为吻合的.由此可见，在氯离子侵蚀、荷载作用和潮水冲刷等多种作用下，该临海水闸混凝土的抗氯性能严重降低，使用寿命大为减少，其钢筋锈蚀的临界氯离子浓度为0.12%～0.18%.计算结论也表明，用Monte Carlo法预测钢筋初锈时间是可行的.

3.3 用氯离子平均扩散系数预测钢筋初锈时间

上述计算是将该水闸在服役5 350d后的氯离子扩散系数作为恒定的扩散系数.实际上，混凝土中的氯离子扩散系数随暴露时间t的延长而不断降低［9－10］.因此，采用当前时刻氯离子浓度所拟合的扩散系数来预测钢筋初锈时间，其结果将比实际时间要晚.

文献［10］将混凝土中的氯离子扩散系数随时间增加而降低的现象用幂函数表征，得到的氯离子扩散系数模型为：

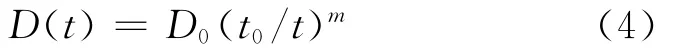
式中：m为时间衰减系数，与水灰比有关；t0为混凝土养护龄期，d；D0为参考期（一般为28d）扩散系数，m2／s.

已有研究表明，水灰比对m的影响大致呈线性下降关系［6，9］.文献［8］中分别计算了服役37a，混凝土水灰比为0.59的甲水闸，以及混凝土水灰比为0.61且服役27a的乙水闸氯离子扩散系数，得到这两座水闸闸墩混凝土中氯离子扩散系数随时间的衰减系数，甲水闸为0.603，乙水闸为0.562.由此，可得到混凝土中氯离子扩散系数的时间衰减系数m与混凝土水灰比mW／mC的关系为：

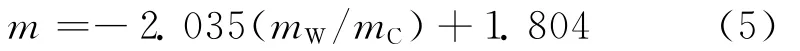
再结合本文背景工程推定的混凝土配合比，得出水灰比为0.55的该临海既有水闸闸墩混凝土中氯离子扩散系数随时间的衰减系数为0.684，则该水闸闸墩混凝土中氯离子扩散系数随时间变化的模型为：

在已知t0，t和闸墩混凝土在当前时刻的氯离子扩散系数Dt的情况下，可以由式（6）推出初始氯离子扩散系数D0.因此，可得出此水闸闸墩混凝土在服役期内的氯离子平均扩散系数Dav：

将上述氯离子平均扩散系数Dav代入式（3）中来计算钢筋初锈时间，其结果应与实际情况更为吻合.对于本文的既有水闸闸墩混凝土，取t0＝28d，t＝5 350d，在模拟求出每个芯样的Dt后先用式（6）求出其初始扩散系数D0；将D0代入式（7）中，分别求出闸门上、下游混凝土中氯离子平均扩散系数Dav的5个样本值.以上游3号芯样为例，由式（2）得到当前时刻的Dt＝2.772×10－13m2／s，再用式（6）计算出D0＝1.008×10－11m2／s，最后用式（7）得出其氯离子平均扩散系数Dav＝7.113×10－13m2／s.

分析闸门上游和下游混凝土中氯离子平均扩散系数Dav的统计参数，其结果符合对数正态分布.取临界氯离子浓度均值为0.18%，0.12%，0.06%，仍然利用式（3）即Monte Carlo法模拟10 000次，得出上游混凝土中钢筋初锈时间分别为3 445，3 351，946d，下游混凝土中钢筋初锈时间分别为3 270，2 609，995d.

在临界氯离子浓度均值相同的情况下，采用当前氯离子浓度拟合的扩散系数Dt所计算的钢筋初锈时间比采用Dav计算的结果要迟100d左右.从计算结果分析，两者比较接近，其主要原因是既有混凝土在自然环境下承受多种因素作用，混凝土早期的氯离子扩散系数衰减十分显著，而后期则变化极为缓慢并趋于稳定［9，11］，以致其平均值与当前时刻的Dt值相差不大.

3.4 考虑氯离子扩散系数时变性的钢筋初锈时间

预测

将式（6）代入式（3）中，可得到考虑氯离子扩散系数随时间变化的钢筋初锈时间t的预测公式：

式中的混凝土养护龄期t0＝28×24×60×60＝2 419 200s.根据式（6）依次求出上游和下游芯样的初始氯离子扩散系数D0，并分析其统计参数，取临界氯离子浓度均值为0.18%，0.12%和0.06%，利 用Monte Carlo法计算式（8），模拟10 000次后得出上游混凝土中钢筋初锈时间分别为3 092，2 115，823d，下游混凝土中钢筋初锈时间分别为2 859，2 180，818d.

在临界氯离子浓度均值相同的情况下，采用平均氯离子扩散系数Dav所计算的钢筋初锈时间比采用当前时刻氯离子浓度拟合的扩散系数所直接计算的钢筋初锈时间要早，而采用考虑扩散性能随时间衰减的D（t）值所计算的钢筋初锈时间则最早.但3种情况总体上较为接近，因为混凝土早期的氯离子扩散系数衰减十分显著，后期则变化缓慢，计算时其对钢筋初锈时间的贡献逐渐减少，因此三者相差并不大.

根据CECS220：2007《混凝土结构耐久性评定标准》，本文中闸墩混凝土可按墙、板（非角部钢筋）来计算临界钢筋锈蚀深度δcrit.计算时，闸墩混凝土中所用钢筋直径为20mm，混凝土强度等级为C20（立方体抗压强度标准值fcu，k取20MPa），保护层厚度为35mm，得到临界钢筋锈蚀深度为0.08mm.而水闸运行5 350d后，计算得到的上、下游混凝土中钢筋锈胀裂缝宽度分别为0.62，0.78mm，与取样时裂缝最大宽度不大于1.0mm较为吻合.

4 结论

（1）处于自然临海环境下使用5 350d的临海水闸闸墩混凝土中存在明显的氯离子对流区，其厚度约为24mm，其后氯离子浓度随深度逐渐下降.

（2）在自然临海环境下，混凝土中钢筋锈蚀的临界氯离子浓度为0.12%～0.18%，预测的钢筋初锈时间约为3 000d，与实际情况吻合.

（3）用服役期内混凝土的氯离子平均扩散系数Dav能有效预测钢筋初锈时间，其结果与用当前时刻氯离子浓度拟合的扩散系数Dt所计算的结果相近.但采用考虑扩散性能随时间衰减的D（t）值所计算的钢筋初锈时间则最早.

（4）采用Monte Carlo方法，用当前时刻氯离子浓度拟合的氯离子扩散系数来预测钢筋初锈时间是可行的.

［1］ 赵羽习，王传坤，金伟良，等.混凝土表面处氯离子浓度时变规律试验研究［J］.土木建筑与环境工程，2010，32（3）：8－13.ZHAO Yuxi，WANG Chuankun，JIN Weiliang，et al.Experimental analysis on time－dependent law of surface chloride ion concentration of concrete［J］.Journal of Civil，Architectural ＆Environmental Engineering，2010，32（3）：8－13.（in Chinese）

［2］ LINDVALL A.Chloride ingress data from field and laboratory exposure—Influence of salinity and temperature［J］.Cement ＆ Concrete Composites，2007，29（2）：88－93.

［3］ 张俊芝，王建泽，孔德玉，等.既有水工混凝土氯离子扩散系数的时变模型［J］.水利水运工程学报，2010（2）：14－20.ZHANG Junzhi，WANG Jianze，KONG Deyu，et al.Time variation model of chloride ions'diffusion coefficient for existing concrete［J］.Hydro－Science and Engineering，2010（2）：14－20.（in Chinese）

［4］ 张俊芝，孔德玉，王建泽，等.一种推定硬化混凝土配合比的方法：中国，200910098028.2［P］.2010－12－08.ZHANG Junzhi，KONG Deyu，WANG Jianze，et al.An inferring method of mix proportion of hardened concrete：China，200910098028.2［P］.2010－12－08.（in Chinese）

［5］ 鲁列.荷载与氯盐环境下混凝土构件的腐蚀试验研究［D］.杭州：浙江工业大学，2010.LU Lie.Study on penetration experiment of RC members under loading and chloride environment［D］.Hangzhou：Zhejiang University of Technology，2010.（in Chinese）

［6］ 金伟良，袁迎曙，卫军，等.氯盐环境下混凝土结构耐久性理论与设计方法［M］.北京：科学出版社，2011：58－67.JIN Weiliang，YUAN Yingshu，WEI Jun，et al.Durability theory and design method of RC structure in chloride environment［M］.Beijing：Science Press，2011：58－67.（in Chinese）

［7］ 张俊芝，郑辉，周建民，等.自然扩散法预测感潮环境下混凝土氯离子侵蚀［J］.建筑材料学报，2011，14（2）：164－168，179.ZHANG Junzhi，ZHENG Hui，ZHOU Jianmin，et al.Erosion prediction of chloride ions in existing concrete under the natural tidal environment by the natural diffusion method［J］.Journal of Building Materials，2011，14（2）：164－168，179.（in Chinese）

［8］ 郑辉.自然环境下混凝土氯离子侵蚀的随机性及寿命预测［D］.杭州：浙江工业大学，2009.ZHENG Hui.Randomness of chloride ion erosion in concrete and service life prediction under natural environment［D］.Hangzhou：Zhejiang University of Technology，2009.（in Chinese）

［9］ 张俊芝，周剑，鲁列.暴露与养护时间对混凝土氯离子扩散性能的影响［J］.自然灾害学报，2011，20（1）：1－5.ZHANG Junzhi，ZHOU Jian，LU Lie.Influence of exposure and curing time on performance of chlorine ion diffusion inconcrete［J］.Journal of Natural Disasters，2011，20（1）：1－5.（in Chinese）

［10］ MANGAT P S，MOLLOY B T.Prediction of long term chloride concentration in concrete［J］.Materials and Structure，1994，27（6）：338－346.

［11］ 刘文军，王军强.氯离子对钢筋混凝土结构的侵蚀分析［J］.混凝土，2007（4）：20－22.LIU Wenjun，WANG Junqiang.Analysis of chloride ion diffusion in reinforced concrete structures［J］.Concrete，2007（4）：20－22.（in Chinese）