基于不同算法的道路混凝土干缩神经网络预测

周胜波， 申爱琴， 张 远， 万晨光， 赵洪基

（1.长安大学 公路学院，陕西 西安 710064；2.广西交通科学研究院 广西道路结构与材料重点实验室，广西 南宁 530007）

混凝土的干缩预测通常采用基于数学回归分析方法的数学模型，主要包括ACI干缩预测模型［1］，Bazant－Panula模型［2］以及 CEB－FIP 模型［3］等.然而，这些模型仅适用于特定条件下的研究对象，限制了其广泛应用.人工神经网络［4］是一种类似于大脑神经突触的连接结构，可以进行信息处理的非线性分析，利用其网络的自学习、联想及存储功能，同时借助计算机高速运算能力可很快找到最优解.基于人工神经网络理论建立混凝土干缩率预测模型，不仅可以避免猜测表达式的烦恼，而且可以综合分析所有试验数据，得到的参数也更加可信，并且便于推广应用到一般情况.近年来，国内外学者开展了神经网络用于混凝土研究的实践.Ghaboussi等［5］应用神经网络方法研究了结构损伤问题；Eldin等［6］采用神经网络模型对橡胶混凝土的抗压强度和抗弯强度进行了预测；孙名松等［7］用人工神经网络方法研究钢筋混凝土双向偏心受压构件的强度计算，建立了一个四层网络；王恒栋等［8］用人工神经网络方法计算混凝土的碳化值；Song等［9］用神经网络算法预测高性能混凝土的氯离子渗透系数；Parichatprecha等［10］用人工神经网络对高性能混凝土耐久性进行了分析；Atici［11］用多元线性回归分析方法和人工神经网络方法对掺有矿物掺合料混凝土强度进行了分析比较，指出人工神经网络模型在处理非线性问题具有更优异的性能；许利惟等［12］用反向传播神经网络对高性能混凝土自收缩进行了预测；Bal等［13］用四层神经网络对混凝土干缩进行了预测.但是，用神经网络进行道路混凝土干缩预测的研究报道很少.误差反向传播神经网络（简称BP神经网络）是人工神经网络中应用最广泛的一种神经网络，本文针对混凝土早期收缩在水泥用量、用水量、粗细集料体积比、骨料体积含量、减水剂和引气剂等多种因素影响下数学模型难以建立的难题，开展了道路混凝土干缩试验，基于BP神经网络理论建立了用于道路混凝土干缩预测的神经网络模型，并通过试验数据对该模型的有效性进行了验证.

1 试验设计及方法

试验原料选用秦岭P·O42.5R水泥；细集料为西安灞河中砂；粗集料为陕西泾阳碎石，最大粒径31.5mm；减水剂为山西恒升高效减水剂，减水率（质量分数）16%～25%；引气剂为Sky型高效引气剂；自来水.干缩试验按照JTG E30—2005《公路工程水泥及水泥混凝土试验规程》进行，测试龄期为1，2，3，4，5，6，7d.道路混凝土配合比如表1所示.

表1 道路混凝土配合比Table 1 Mix proportion of pavement cement concrete

2 BP神经网络模型设计

根据Kolmogorov定理，给定任一连续函数f：X→Y，其中X是闭区间［0，1］.由于f可通过1个三层前馈网络实现，因此本文选择含有输入层、隐含层和输出层的三层神经网络结构.p为输入向量，p＝p1，p2，…，p6，分别对应混凝土材料组成中的6个变量：水泥用量，用水量，粗细集料体积比，粗骨料体积分数，引气剂掺量和减水剂掺量，故输入单元个数m为6；t为输出向量，对应干缩率，因此输出单元个数n为1；隐含层神经单元个数对神经网络性能有一定影响，节点数过少会使网络容错性差，节点数过多会增加网络训练时间，且降低泛化能力，本文根据经验公式l＝（l为隐含层节点数，α为1～10的条件常数）进行设计，在4～14之间根据网络训练情况确定l值.

神经网络结构层之间的传递通过激励函数实现，不同的隐含层和输出层传递函数对BP神经网络的预测精度有较大影响［14］，本文隐含层节点传递函数选择Tansig，考虑到Sigmoid函数将整个网络输出限制在一个较小的范围，输出层节点传递函数选为Purelin函数.预测道路混凝土干缩神经网络算法流程见图1.

混凝土干缩试验共计27个配合比，每个配合比测试7个龄期的干缩数据，随机选取23个配合比即161组试验数据作为神经网络训练样本，剩余4个配合比的28组试验数据作为验证样本.为避免因输入、输出数据数量级差别造成神经网络预测误差大的问题，本文用最大最小法把数据归一化成［0，1］，最大最小法函数如下：x′k＝ （xk－xmin）／（xmaxxmin），式中xmin为数据序列中最小数，xmax为序列中最大数.

网络训练基于Matlab7.0软件通过编程实现.为了比较不同算法下神经网络的性能差异，共选择了 Traingd，Traingdm，Traingda，Traingdx，Trainlm这5种函数进行训练，学习速率在0.01～0.50之间取值，动量因子在0.75～1.05之间取值，训练最大迭代次数为20 000次，误差目标均方差为0.03.BP神经网络的Matlab实现过程见图2.

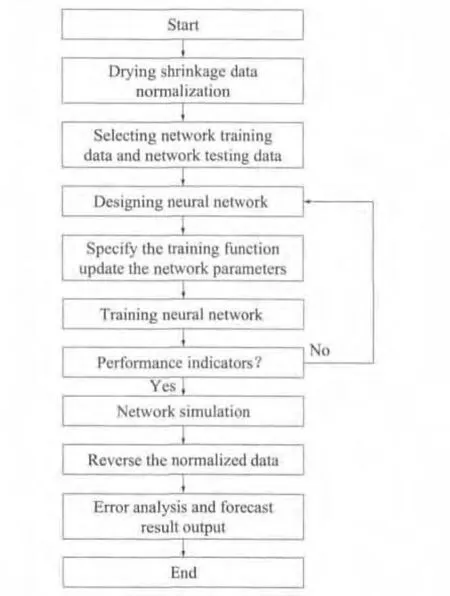
图2 BP神经网络的Matlab实现过程Fig.2 Matlab process of BP neural network

3 干缩预测神经网络模型分析

为了优化BP神经网络模型，提高其泛化能力，本文对5种算法训练神经网络的性能指标进行了综合比较，结果如表2.由表2可见，不同算法下神经网络都能满足收敛目标0.03的要求，相比之下收敛速度较快的Trainlm函数经4～300次可结束训练，Traingd和Traingdm函数收敛速度较慢，而Traingda和Traingdx函数的训练速度居中.但是，过于追求训练速度的Trainlm函数在预测道路混凝土干缩时误差较大，因此不适合作神经网络训练函数.由均方差（MSE）、误差平方和（SSE）以及最大相对误差（MAX RE）综合分析可知，Traingda和Traingdx函数不仅训练速度快、误差小，且其MSE，SSE和另外3种函数相当，道路混凝土干缩预测的最大相对误差为7.05%.表2为不同算法训练神经网络综合性能比较.

采用不同算法优化后的神经网络预测道路混凝土干缩率与试验值对比见图3.由图3可见，除Trainlm存在较大的波动外，其他算法训练的神经网络均可较好预测不同龄期道路混凝土的干缩率，尤其是用Traingda函数训练的神经网络预测道路混凝土干缩效果更优.

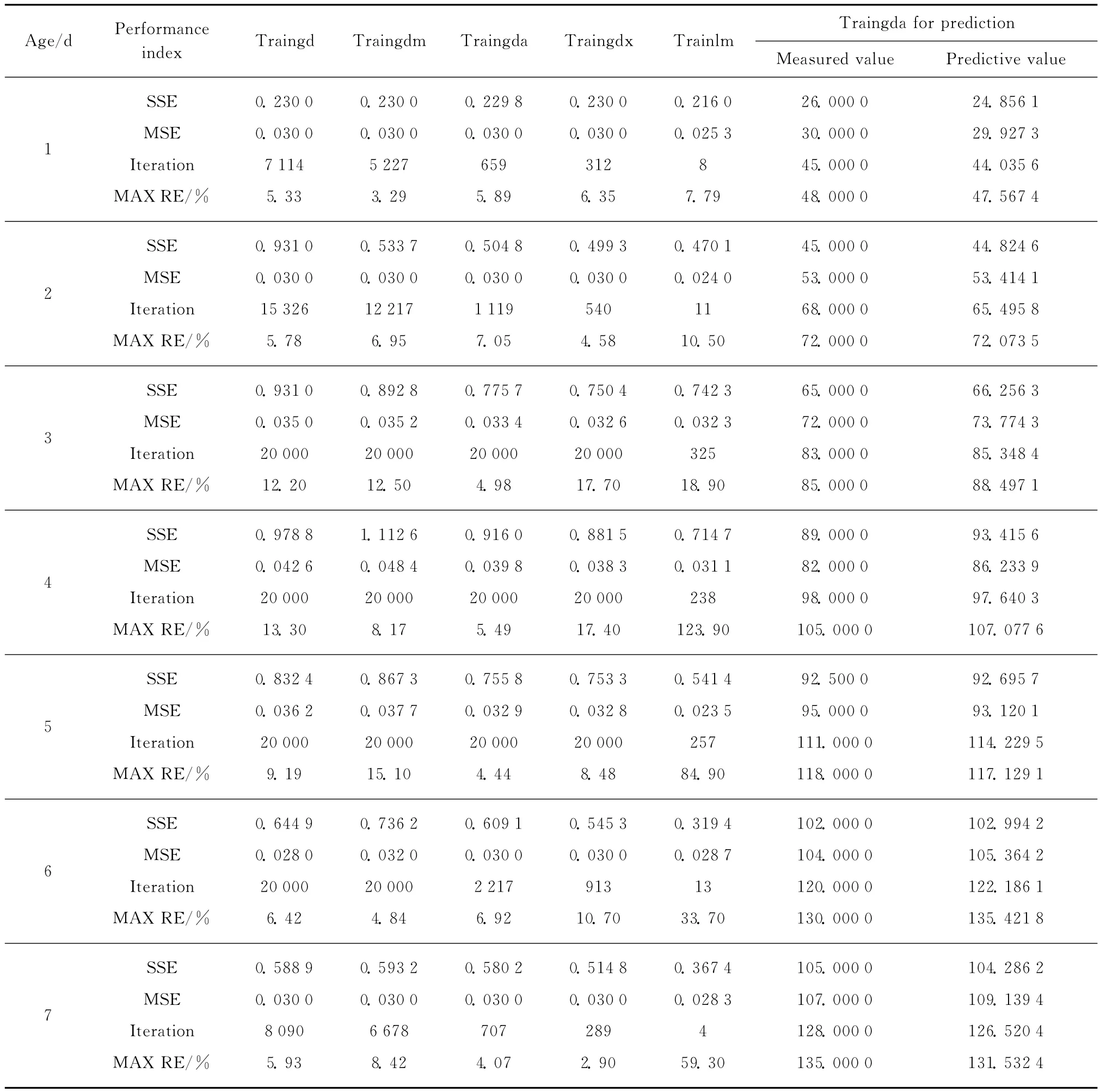
表2 不同算法训练神经网络综合性能比较Table 2 Comprehensive performance comparison of neural network using different algorithms for training

本文选择已有的干缩预测模型对4个配合比道路混凝土干缩率进行了预测，这些干缩预测模型包括 ACI模型、Bazant－Panula模型、CEB－FIP模型.在进行预测时，由于没有测量最大应变，只好用其他龄期的应变和2d龄期的应变进行比较以消除最大应变的影响，结果见表3，其中ε的右下标数字表示第几天.由表3可见，采用上述3个模型预测道路混凝土干缩误差较大（2.00%～30.00%），而神经网络模型的干缩预测效果最佳，最大误差为6.84%.因此，基于不同混凝土配合比采用神经网络能够映射其与干缩率的非线性关系，不仅克服了其他干缩预测模型中人为猜测函数形式及其参数难以确定的困难，而且能够准确描述混凝土的干缩程度.

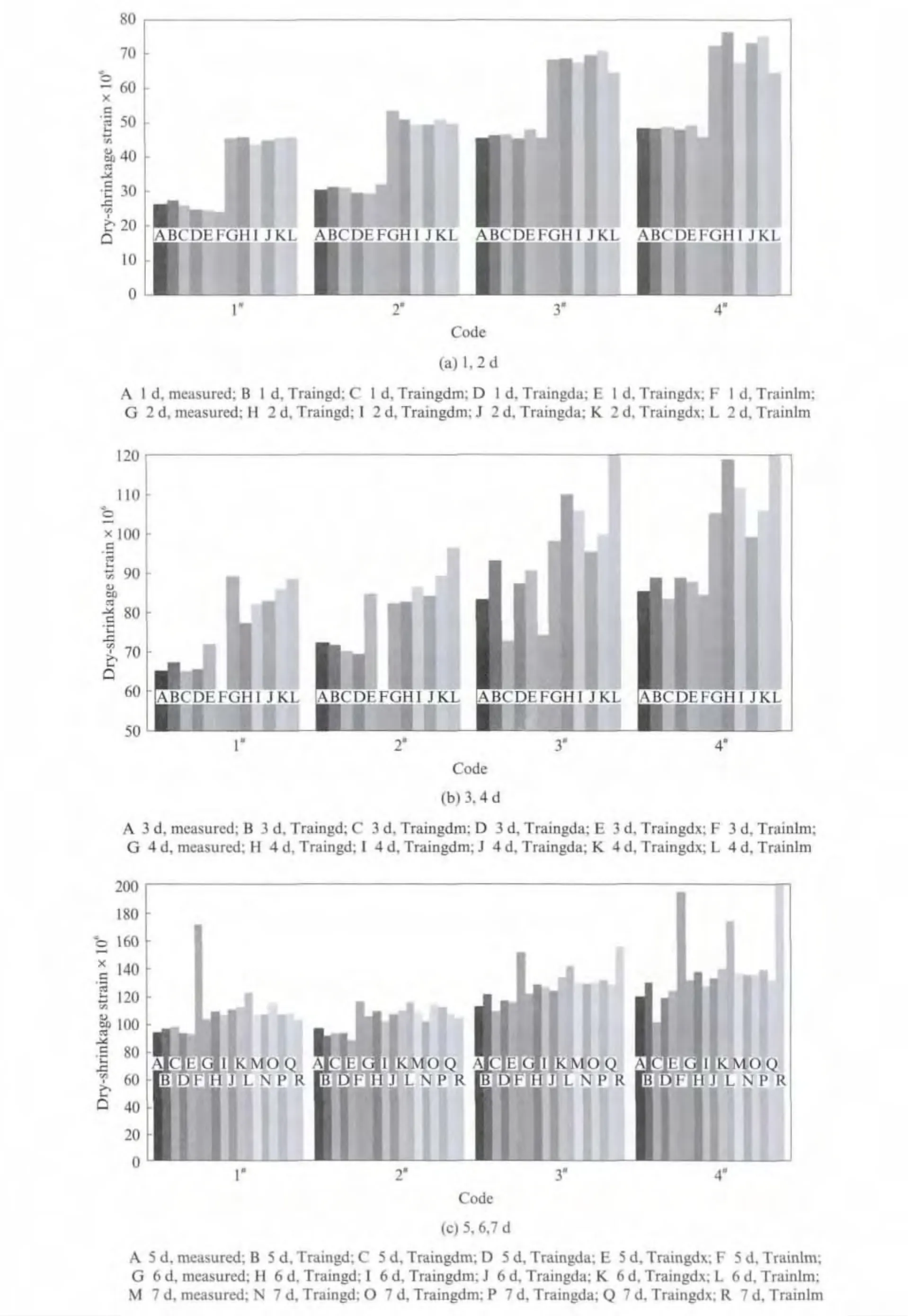
图3 道路混凝土干缩率预测值与试验值对比Fig.3 Comparison of predicted value and measured value of dry shrinkage using different training function

表3 不同干缩模型预测值与试验值比较Table 3 Comparison of predicted value and measured value from different prediction model for dry shrinkage

4 结论

（1）基于道路混凝土原料组成，运用BP神经网络进行相应的干缩率预测可以得到比较精确的结果.

（2）在5种训练函数中，用Traingda函数训练的神经网络进行道路混凝土干缩率预测效果最佳，在本试验范围内，其最大相对误差为7.05%.

（3）用神经网络方法建立道路混凝土干缩预测模型可有效避免其他预测模型建立的难题及人为因素造成的误差.

［1］ ACI209－82 Prediction of creep，shrinkage and temperature effects in concrete structures［S］.

［2］ BAZANT Z P.Creep and shrinkage prediction model for analysis and design of concrete structures－model B3［J］.Materials and Structure，1995，28（3）：357－365.

［3］ CEB－FIP Model code for concrete structures［S］.

［4］ HAGAN M T，DEMUTH H B.神经网络设计［M］.戴葵译.北京：机械工业出版社，2002：25－44.HAGAN M T，DEMUTH H B.Neural network design［M］.Translated by DAI Kui.Beijing：China Machine Press，2002：25－44.（in Chinese）

［5］ GHABOUSSI J，GARRETT J H.Use of neural networks in detection of structural damage［J］.Computers and Structures，1992，42（4）：649－659.

［6］ ELDIN N N，SENOUCI A B.Measurement and prediction of the strength of rubberized concrete［J］.Cement and Concrete Composites，1994，16（4）：287－298.

［7］ 孙名松，宿延吉.人工神经网络在钢筋混凝土试验研究中的应用［J］.哈尔滨电工学院学报，1995，18（1）：67－72.SUN Mingsong，SU Yanji.Application of artificial neural network in the research of reinforced concrete testing［J］.HIET Journal，1995，18（1）：67－72.（in Chinese）

［8］ 王恒栋，赵国藩.基于人工神经网络的混凝土碳化分析［J］.水运工程，1996（1）：9－11.WANG Hengdong，ZHAO Guofan.Analysis of concrete carbonation based on artificial neural network［J］.Port ＆ Waterway Engineering，1996（1）：9－11.（in Chinese）

［9］ SONG Hawon，KWON Seungjun.Evaluation of chloride penetration in high performance concrete using neural network algorithm and micro pore structure［J］.Cement and Concrete Research，2009，39（9）：814－824.

［10］ PARICHATPRECHA R，NIMITYONGSKUL P.Analysis of durability of high performance concrete using artificial neural networks［J］.Construction and Building Materials，2009，23（2）：910－917.

［11］ ATICI U.Prediction of the strength of mineral admixture concrete using multivariable regression analysis and an artificial neural network［J］.Expert Systems with Applications，2011，38（8）：9609－9618.

［12］ 许利惟，郑建岚.基于BP神经网络的高性能混凝土早龄期自干燥收缩预测［J］.福建工程学院学报，2008，6（1）：8－12.XU Liwei，ZHENG Jianlan.Prediction of high performance concrete self－desiccation shrinkage at early age based on BP neural network［J］.Journal of Fujian University of Technology，2008，6（1）：8－12.（in Chinese）

［13］ BAL L，BUYLE－BODIN F.Artificial neural network for predicting drying shrinkage of concrete［J］.Construction and Building Materials，2013，38（1）：248－254.

［14］ 史峰，王小川.Matlab神经网络30个案例分析［M］.北京：北京航空航天大学出版社，2010：11－20.SHI Feng，WANG Xiaochuan.Matlab neural network and 30 case analysis［M］.Beijing：Beijing University of Aeronautics and Astronauties Press，2010：11－20.（in Chinese）