开放体系中抗体- 抗原复合物生长的Monte Carlo模拟

张平

（承德医学院生物医学工程系，河北承德 067000）

开放体系中抗体- 抗原复合物生长的Monte Carlo模拟

张平

（承德医学院生物医学工程系，河北承德 067000）

为了研究更接近于真实的免疫反应系统中抗体 抗原复合物的生长，提出了一个开放的抗体 抗原系统模型，在这一体系中抗体、抗原分子能以一定的方式产生并参与反应.通过Monte Carlo模拟方法分别考察了线性体系和支化体系的演化过程，所采用的算法包含了一个自洽的叠代方法计算等待时间，以此算法为基础，研究了抗体和抗原分子不同输入方式对复合物数均和重均聚合度的影响，发现不同体系在演化过程中的相关统计特征都可以反映输入方式的变化，因而可以通过观测平均物理量来识别输入方式.

抗体-抗原复合物；开放体系；Monte Carlo模拟

抗体与抗原的相互作用导致抗体 抗原复合物的形成和生长，这一过程在生物体的免疫机制中起着非常重要的作用［1－3］.在医学临床应用上，抗体抗原反应是免疫检测的基础［4］.因此，长期以来，人们对抗体与抗原的相互作用及抗体 抗原复合物的研究表现出极大的关注［5－14］.

对抗体 抗原复合物平衡性质及时间演化的研究，一般除了采用等活性和忽略内环化这样的近似之外，还要求系统是封闭的，这使其应用受到一定的限制.为了解抗体-抗原复合物对免疫应答的调解作用机制，对于动态开放的抗体-抗原体系的研究是非常必要的.

对于一个更为实际的体系而言，在抗体-抗原复合物生长过程中，抗体和抗原分子往往均能以一定的方式产生并参与反应.例如，按照克隆选择学说，当有一定的抗原进入体内时，抗原和B细胞表面受体结合可以使B细胞激活，激活的B细胞不断繁殖并可产生和分泌抗体.相对于此前的“封闭”系统而言，这种在反应过程中允许不断加入抗体和抗原分子的体系可被称作“开放”体系.为了更加直观地说明“开放”体系的相关特征，本文以图1示意如下：在“开放”的抗体 抗原体系中，描述抗体-抗原复合物生长的动力学方程将有别于“封闭”体系的动力学方程.因此，可以预期抗体 抗原体系相关的统计特征亦将有别于“封闭”体系的相应结果.对“开放”的抗体 抗原体系而言，抗体和抗原分子的不断输入实际上可以视作是外界对体系的一种“刺激”.相应地，作为对外部刺激的响应，体系的一些相关统计特征应该可以反映抗体或抗原分子输入方式的变化.

图1开放的抗体 抗原体系示意Fig.1 A schematic figure of the growth of Ab-Ag complexes in open system

应该指出的是，“开放”体系模型更加接近于体内的抗体 抗原反应过程，因此相应的研究更具实际意义.本文以Monte Carlo模拟方法来研究抗体和抗原分子不同输入方式对复合物数均和重均聚合度的影响，从而为相关实验提供定量或半定量的理论依据，深化对抗体-抗原相互作用的认知.

由于“开放”体系中抗体、抗原分子不断以不同方式输入，因此在确定等待时间tW的问题上必须谨慎对待，这同时也是“开放”体系Monte Carlo模拟算法的关键所在.为此，在模拟中采用了一种自洽迭代计算的方式来确定等待时间tW.进一步，为了考察不同输入方式对复合物数均和重均聚合度的影响，模拟中人为地设定了正弦输入、方波输入、三角波输入和匀速输入等几种连续输入方式.模拟结果正如所期待的那样，通过考察体系的数均和重均聚合度随时间的变化情况的确可以区分不同的输入方式，从而实现了确定体系“刺激-响应”因果关系的目的.

1 模拟方法

考虑一个动态开放的抗体 抗原相互作用系统，假设系统最初包括一定数目的价性为b的抗体分子和价性为g的抗原分子，此后，抗体、抗原单体分子按一定方式输入.显然，这样动态开放体系中的抗体 抗原复合物的生长动力学必然与输入方式直接相关.为了探讨输入方式的影响，需要对体系的平均特征予以研究.不失一般性，以Cm，l（t）表示t时刻由m个抗体分子和l个抗原分子形成的复合物，则抗体 抗原复合物生长过程可表示为

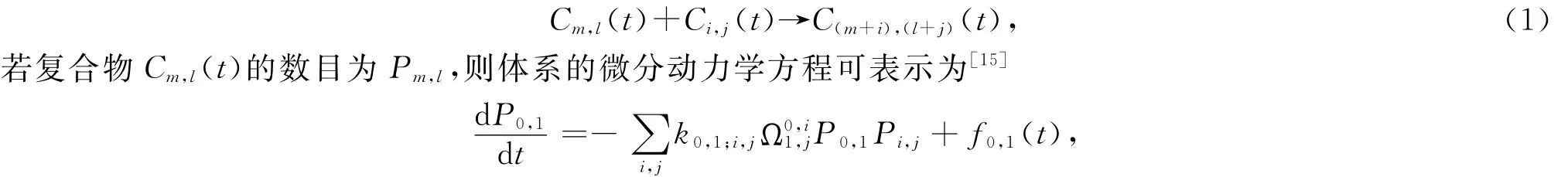
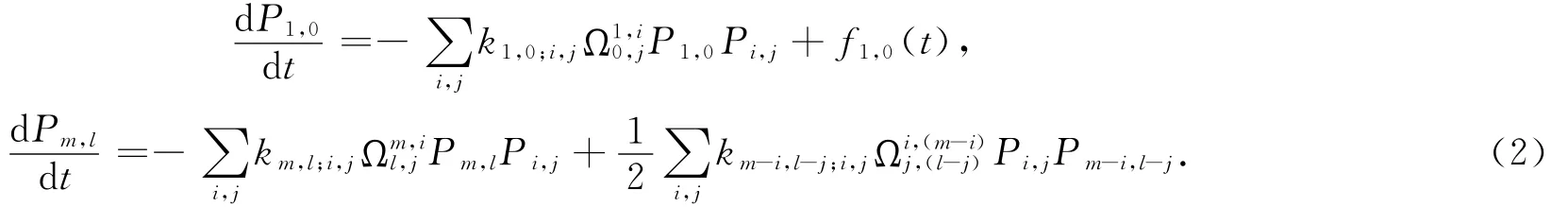
上面各式描述了体系中各种成分的确定性的时间演化方式，其中f0，1（t）和f1，0（t）分别是抗体和抗原单体输入速率函数表示Cm，l（t）和Ci，j（t）间的结合方式数，而km，l；i，j是相应的结合速率常数.一般情况下，各个km，l；i，j值并不相等，为此可以引入反应活性参数R＝k1，1／kP，P，其中k1，1表示单体-单体的结合常数，kP，P表示单体-多聚体及多聚体-多聚体的结合常数.当R＝1时，系统中各成分的结合速率常数都相等，此时各km，l；i，j可以统一用k表示.本文中为了使问题简化，笔者只就R＝1的情况进行研究.

对于开放体系，由于抗体、抗原分子不断输入，通过微分动力学方程一般无法获得体系数量分布函数的解析解，因此通过随机模拟方法［16－17］来研究体系的演化过程便充分显示出其必要性和有效性.本文中所用的Monte Carlo模拟算法较此前我们的方法［18］有了较大的突破，即在确定等待时间tW的问题上给予了特别的考虑，对不同的输入方式进行了区别对待.下面对模拟算法予以简要说明.

假定体系最初仅存在抗体和抗原分子（单体），此后抗体-抗原复合物按照方程（2）所示的方式演化.若以｛Pm，l（t）｝表示t 时刻系统中抗体-抗原复合物的状态，则此后dt 时间内抗体 抗原复合物形成的转变概率为

由此可知，等待时间tW是满足指数分布的一个随机变量，此即反应时间的随机性.通过直接抽样方法，可将等待时间tW与一个随机数r1通过下式关联在一起：

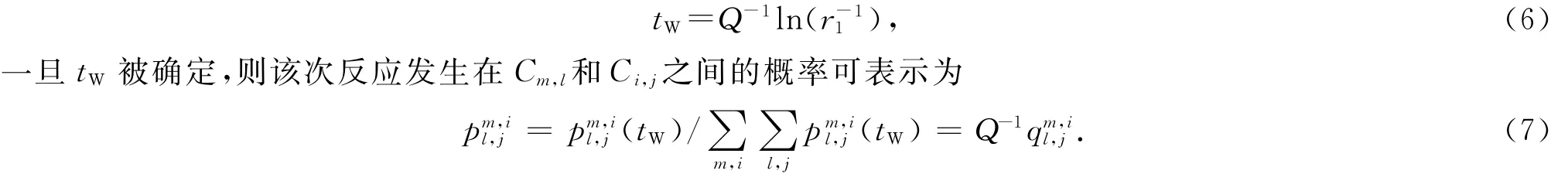
对于有单体不断输入的动态体系，如何确定tW的问题变得比静态封闭体系复杂得多，因为在tW间隔内可能会有一定数量的抗体、抗原单体加入体系，使Q发生改变，进而又对等待时间产生影响.为此，在模拟中采用了一种自洽迭代计算的方式来确定等待时间tW.在这种情况下，通过直接抽样方法可以得到如下方程：

然后通过用迭代方法求方程近似解便可以得到tW，同时也得到了调整后系统中的抗体和抗原的单体数目.一旦tW被确定，便可以获得Q（tW），则该次反应发生在Cm，l（t）和Ci，j（t）之间的概率可表示为＝Q（tW）－1.在此基础上确定反应类型，此时可通过另一个单位区间均匀分布的随机数r2对样本空间中随机事件进行直接抽样来决定.

根据以上分析，可得开放体系的抗体-抗原复合物生长过程的Monte Carlo算法如下：

1）系统初始化（输入初始分子数、价性和确定单体输入方式等）；2）给出随机数r1，通过迭代方法计算tW，调整单体数，确定和Q；3）通过随机数r2确定反应事件类型；4）按照反应事件类型更新系统状态；5）回到步骤（2），直至体系满足预定条件.

2 结果和讨论

2.1 对［Ab］2－［Ag］2体系的模拟

在［Ab］2－［Ag］2体系中，忽略环化反应并设定初始反应条件：在一定体积V中，初始单体数Nb＝1 000，Ng＝1 000；反应速率常数k＝10－6.

模拟中所用各种连续输入方式的函数形式和参数分别为

a）正弦输入方式：设定其函数形式为f（t）＝v［1＋sin（ωt）］，抗体、抗原单体的输入速率皆为v＝1 000，输入周期为T＝2π／ω＝10；

c）三角波输入方式：设定其函数形式为f（t）＝v（t－nT）（n＝0，1，2，…），抗体、抗原单体的输入速率皆为v＝200，T＝10；

d）匀速输入方式：设定其函数形式为f（t）＝v，抗体、抗原单体的输入速率皆为v＝1 000.

以上各种输入方式和参数的选择已经考虑到了简单性和清晰性，为此已使各种输入方式在1个周期内平均输入速率相同，从而便于对比输入方式对体系演化的影响.根据不同的输入方式，并依据相应的Monte Carlo模拟算法可对所研究的体系进行模拟.模拟中主要考察了体系数均聚合度（Dn）和重均聚合度（Dw）的变化，所得结果分别如图2中a，b，c，d各图所示，相应插图是各种输入方式的速率波形.

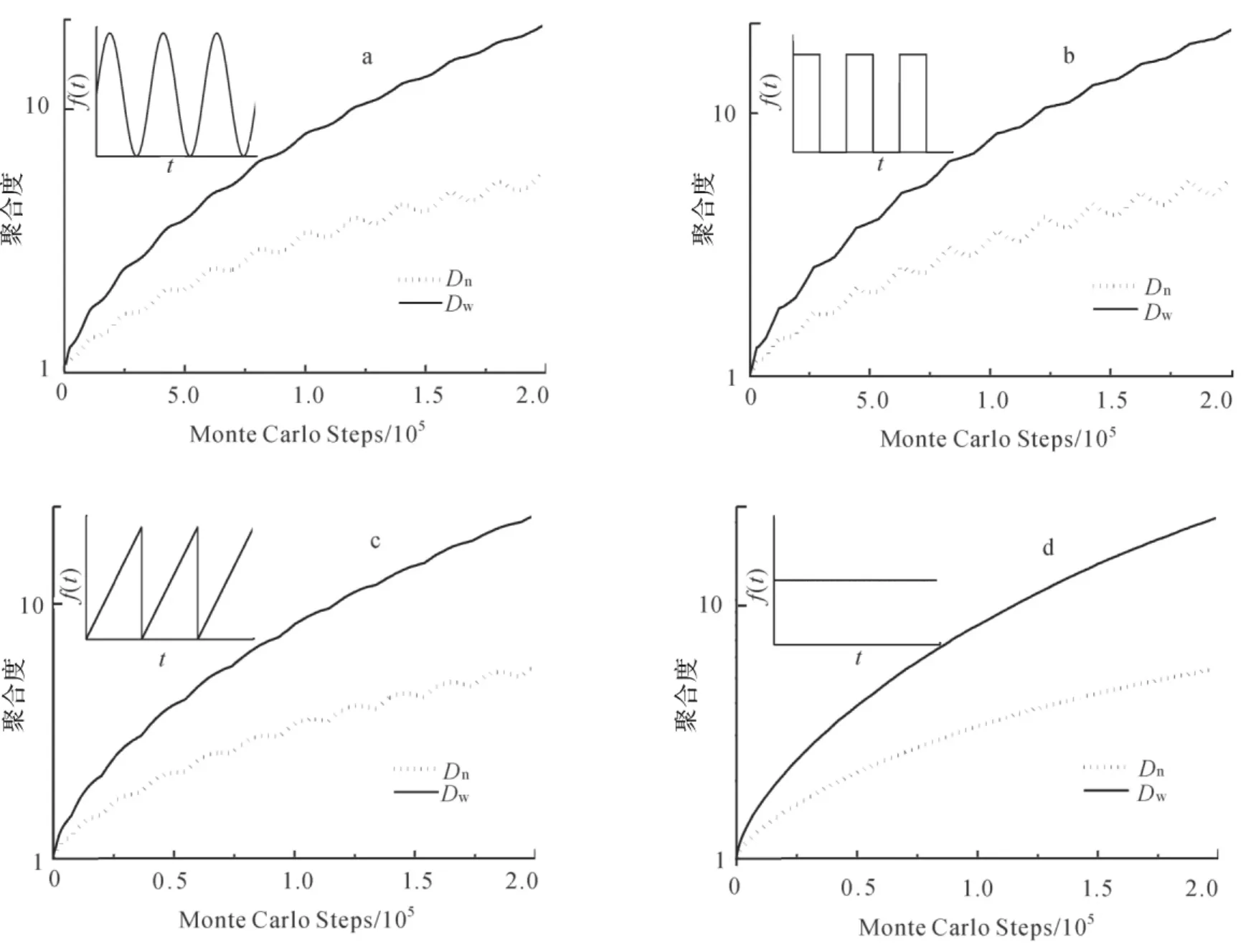
图2 ［Ab］2－［Ag］2体系各种连续输入方式下数均、重均聚合度的演化Fig.2 Evolution of number-and weight-average binding degrees of［Ab］2－［Ag］2 system under the continuous input patterns

由于以上各种输入方式的平均输入速率相同，从图2中可以看到在各种输入方式下体系的数均聚合度和重均聚合度演化曲线总体上具有相似性.然而，在图中一个有趣的特征是平均聚合度随着输入方式的不同而表现出明显不同的波动特性，这说明平均聚合度的演化在一定程度上反映了输入方式的变化，在抗体、抗原的输入和平均聚合度的演化之间，存在着“刺激-响应”因果关系，因而可以通过对平均聚合度的观测来了解、并区分抗体、抗原分子加入体系的不同输入方式.此外，在明确了输入方式和平均聚合度演化的“刺激-响应”关系后，可以据此对体系演化特点的细节加以观察和分析.在以上各图中平均聚合度的波动周期与演化时间相对应，而Monte Carlo Steps 与体系中的抗体-抗原结合对数量相对应.

在此基础上，通过对图2中模拟结果的细节进行观察可知，在体系演化进程中，最初形成抗体-抗原结合对的速率较慢，随后速率逐渐增加并趋于平稳.在整体上，线性体系重均聚合度的增长趋势平缓，且对输入单体数量变化的响应有相对减弱的趋势.而对于数均聚合度而言，其对单体输入变化的响应却随体系中结合对的增加而显著.这是由于随着演化的进行，体系中出现越来越多高聚合度的复合物，同时总的结构单元数增多，从而使单体的输入对重均聚合度演化的影响相对降低；而数均聚合度取决于总分子数和总的结构单元数的比值，因而受单体数变化的影响较明显.

2.2 对［Ab］2－［Ag］3体系的模拟

根据上节提到的相应输入方式，也可以［Ab］2－［Ag］3体系为例对抗体-抗原复合物支化生长过程进行模拟.同样地，模拟中也忽略环化反应并令各种连续输入方式下的反应条件与［Ab］2－［Ag］2体系中相对应的情况完全相同.对于各种瞬时输入方式，为了便于观察其特点，输入量和输入间隔的选取与［Ab］2－［Ag］2体系中对应的情况相比减小一半.各种连续输入方式下系统的数均、重均聚合度的演化模拟结果分别如图3中a，b，c，d各图所示.

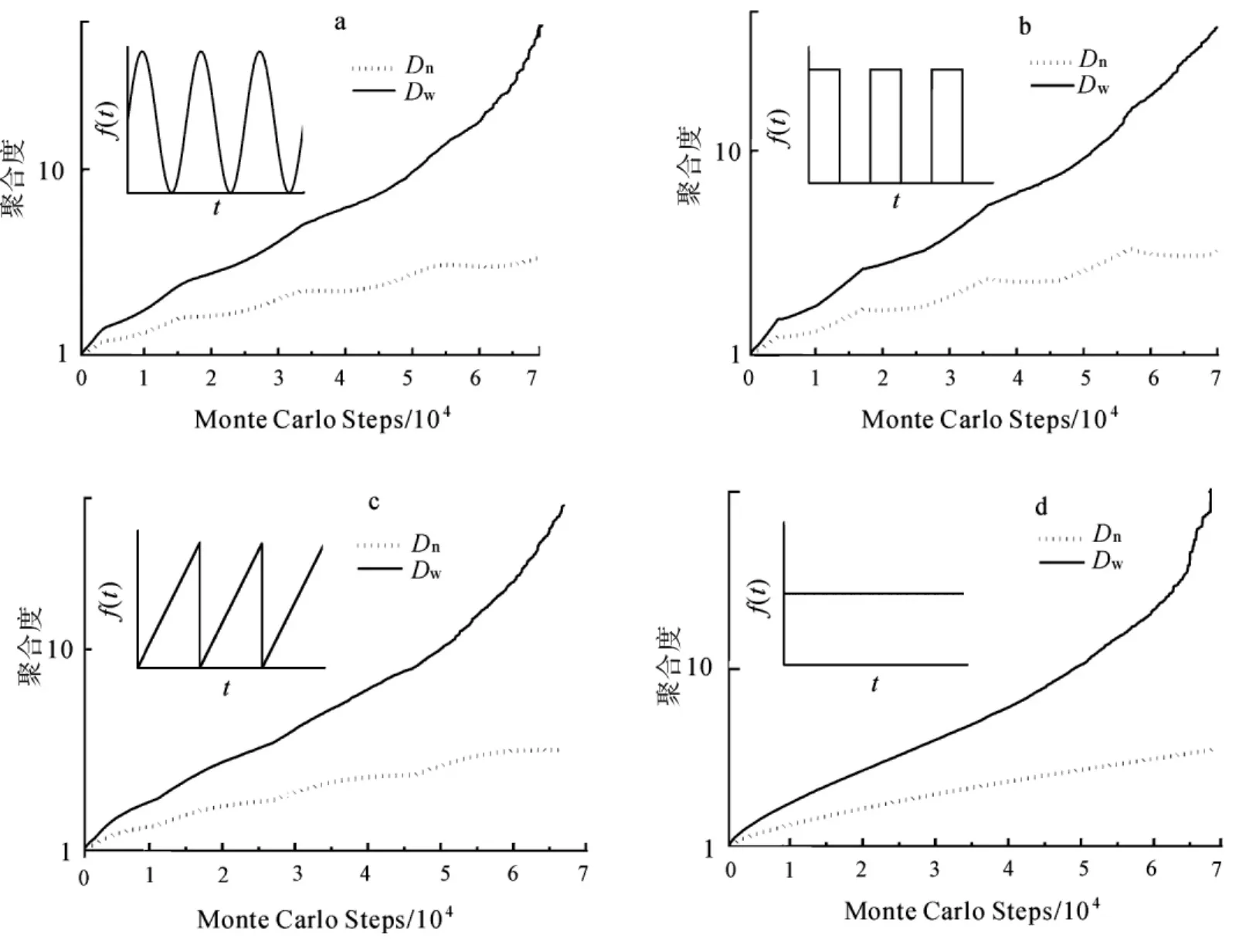
图3 ［Ab］2－［Ag］3体系各种连续输入方式下数均、重均聚合度的演化Fig.3 Evolution of number-and weight-average binding degrees of［Ab］2－［Ag］3 system under the continuous input patterns

对于非线性的抗体-抗原体系而言，平均聚合度的演化同样也在一定程度上反映出输入方式的影响，亦即通过对平均聚合度的观测可以区分不同的输入方式，如图3所示.然而，与线性生长体系相比显著的不同之处在于支化生长体系中复合物的重均聚合度增长较快，在结合对数量相对较少时，重均聚合度已经较大且随着结合对数量的增加有发散趋势.相对而言，在抗体 抗原支化体系的演化过程中，其重均聚合度对单体输入方式的响应弱于线性体系，这是由于对支化生长过程而言，较大的复合物更容易生成，由此产生的结果就是重均聚合度增加较快并且随机性增加，因而体系对单体输入这种刺激所产生的响应随即减弱.

通过考察不同体系及不同输入方式下的平均聚合度演化曲线，可知抗体、抗原分子的输入对体系的相关统计特征产生了影响，因而可以通过观测平均物理量来识别输入方式.鉴于体内环境的复杂性，抗体 抗原体系的开放模型更为接近实际情况.本文所提出的Monte Carlo模拟方法对于深入认识体内抗体与抗原反应形成复合物的过程提供了有益的线索，为了解实时动态的抗体-抗原体系提供了一种研究工具.

［1］ ABBAS A K，LICHTMAN A H.Cellular and Molecular Immunology［M］.Philadelphia：W B Saunders，2003.

［2］ PAUL W E.Fundamental Immunology［M］.Philadelphia：Lippincott Williams ＆Wilkins，2008.

［3］ 林学颜，张玲.现化细胞与分子免疫学［M］.北京：科学出版社，1999.

［4］ 王廷华，李官成，ZHOU Xinfu.抗体理论和技术［M］.北京：科学出版社，2009.

［5］ GOLDBER R J.A theory of antibody-antigen reactions.Ⅰ.Theory for reactions of multivalent antigen with bivalent and univalent antibody［J］.J Am Chem Soc，1952，74：5715-5725.

［6］ GOLDBER R J.A theory of antibody-antigen reactions.Ⅱ.Theory for reactions of multivalent antigen with multivalent antibody［J］.J Am Chem Soc，1953，75：3127-3131.

［7］ PALMITER M T，ALADJEM F.The antigen-antibody reaction.Ⅳ.A quantitative theory of antigen-antibody reactions［J］.J Theo Bio，1963，5：211 -235.

［8］ ALADJEM F and PALMITER M T.The antigen-antibody reaction：Ⅴ.A quantitative theory of antigen-antibody reactions which allows for heterogeneity of antibodies［J］.J Theor Biol，1965，8：8-21.

［9］ ARCHER B G and KRAKAUER H.Thermodynamics of antibody-antigen reactions.2.The binding of bivalent synthetic random coil antigens to antibodies having different antigen precipitating properties［J］.Biochemistry，1977，16：618 -627.

［10］ STEENSGAARD J，JACOBSON C，LOWE J，et al.Theoretical and ultracentrifugal analysis of immune complex formation between monoclonal antibodies and human IgG［J］.Immunology，1982，46：751-760.

［11］ SHIAU L D.A systematic analysis of average molecular weights and gelation conditions for branched immune complexes：the interaction between a multivalent antigen with distinct epitopes and many different types of bivalent antibodies［J］.Biopolymers，1996，39：445 -454.

［12］ LAURENZI I J，DIAMOND S L.Kinetics of random aggregation-fragmentation processes with multiple components［J］.Phys Rev E，2003，67：051103.

［13］ YANG J，MONINE M I，FAEDER J R，et al.Kinetic Monte Carlo method for rule-based modeling of biochemical networks［J］.Phys Rev E，2008，78：031910.

［14］ MONINE M I，POSNER R G，SAVAGE P B，et al.Modeling multivalent liand-receptor interactions with steric constrains on configurations of cell-surface receptor aggregates［J］.Biophysical Journal，2010，98：48 -56.

［15］ 唐敖庆，江元生.三向缩聚反应中的凝胶化问题［J］.科学记录，1958，2（3）：100 -105.

［16］ GILLESPIE D T.Stochastic simulation of chemical kinetics［J］.Annu Rev Phys Chem，2007，58：35-55

［17］ 杨玉良，张红东.高分子科学中的Monte Carlo方法［M］.上海：复旦大学出版社，1993.

［18］ ZHANG Ping，WANG Haijun.Monte Carlo simulation on growth of antibody-antigen complexes：the role of unequal reactivity［J］.Chin Phys Lett，2010，27：038701.

（责任编辑：梁俊红）

Monte Carlo simulation on growth of antibody-antigen complexes in open system

ZHANG Ping
（Biomedical Engineering Department，Chengde Medical College，Chengde 067000，China）

A model of open antibody-antigen system close to the real immune reaction system is put forward，in which antibody（Ab）and antigen（Ag）molecules can be produced someway to take part in the reaction.The growth of antibody-antigen complexes in the linear and branched open systems is studied by the Monte Carlo simulation method，in particular，the algorithm adopted involves a self-consistent iteration method to calculate the waiting time.Then the influence of various input patterns on the number-and weight-average binding degrees of the antibody-antigen complexes is investigated，and it is found that the input pattern can be reflected by the average binding degrees.

antibody-antigen complex；open system；Monte Carlo simulation

O641

A

1000 -1565（2014）05 -0502 -06

10.3969／j.issn.1000 -1565.2014.05.011

2014 -05 -10

河北省教育厅资助项目（z2011136）

张平（1968-），男，河北承德人，承德医学院副教授，主要从事生物物理及高分子化学与物理方向研究.E＿mail：zhangping6810＠126.com