基于偶对约束和马氏距离的半监督模糊聚类算法

李凯，王亮，周宇飞

（河北大学数学与计算机学院，河北保定 071002）

基于偶对约束和马氏距离的半监督模糊聚类算法

李凯，王亮，周宇飞

（河北大学数学与计算机学院，河北保定 071002）

研究了基于偶对约束的半监督模糊聚类，将马氏距离引入到半监督模糊聚类SCAPC（semi-supervised fuzzy clustering algorithm with pairwise constraints）中，获得了一种新的半监督模糊聚类目标函数，通过求解优化问题，提出了一种基于偶对约束和马氏距离的半监督模糊聚类算法M-SCAPC（Modified-SCAPC）.针对选择的标准数据集和人工数据集，对提出的算法M-SCAPC进行了实验研究，并与FCM（fuzzy C-means）、AFCC（active fuzzy constrained clustering）和SCAPC算法的聚类性能进行了比较，表明了提出的算法M-SCAPC在收敛速度和正确率方面的有效性.

半监督聚类；偶对约束；度量学习；马氏距离

1 引入马氏距离的半监督聚类算法M-SCAPC

给定一个具有N个样本的数据集X＝｛xi｜i∈｛1，…，N｝｝，假设集合X中的样本点被分为c个簇S1，S2，…，Sc，并记vk（k∈｛1，…，c｝）表示c个聚类中心，uik表示样本点xi属于簇Sk的隶属度，V和U分别表示由聚类中心构成的集合与由隶属度构成的矩阵.

欧氏距离较适用于球形数据，然而该度量受样本间的相关性影响较大，在处理非球形数据或高维数据时聚类效果较差，同时聚类速度也较慢，而马氏距离在处理相关性较大的数据集时具有较好的效果［6］.针对这种情况，研究了使用马氏距离的半监督聚类，获得了如下的目标函数：

下面给出算法M-SCAPC的描述：

1）初始化最大簇数Cmax，设置簇的阈值e和ε，并初始化簇中心和隶属度；

2）计算协方差矩阵Ck和马氏距离；

3）利用式（3）和（4）分别计算参数β和参数α；

4）计算各簇的势，如果簇的势小于阈值e，则删除该簇，并减少相应簇的数目；

5）根据式（2）计算新的隶属度矩阵，使用（5）更新簇中心；

2 实验结果和分析

为了验证算法M-SCAPC的有效性，选择了UCI中的数据集Iris，Diabetes和Wine；同时也人工生成了数据集Data，该数据集是一个具有3维且包括150个样本点，其簇数为3，每个簇包括50个样本点.实验中选取e＝7，ε＝0.001，从所有样本点中选取10对约束样本点，从而获得约束点对集M和C集合.

2.1 参数α和β与迭代次数的关系

由目标函数可知，参数α和β是M-SCAPC算法中决定约束惩罚项的重要程度的参数，为此通过Iris数据集对提出算法进行了实验研究，随着迭代次数的增加，α值先增加后减少，直至α值趋于稳定.另外，随着迭代次数的增加，β值逐渐减小，并且在迭代的初期，β值比较大，说明聚类还不稳定，对势的影响比较大，随着迭代的进行，聚类数和β值都逐渐稳定下来.另外，β值也受η0的取值影响，η0的取值将影响最终的聚类数目和迭代次数，结果如表1所示.

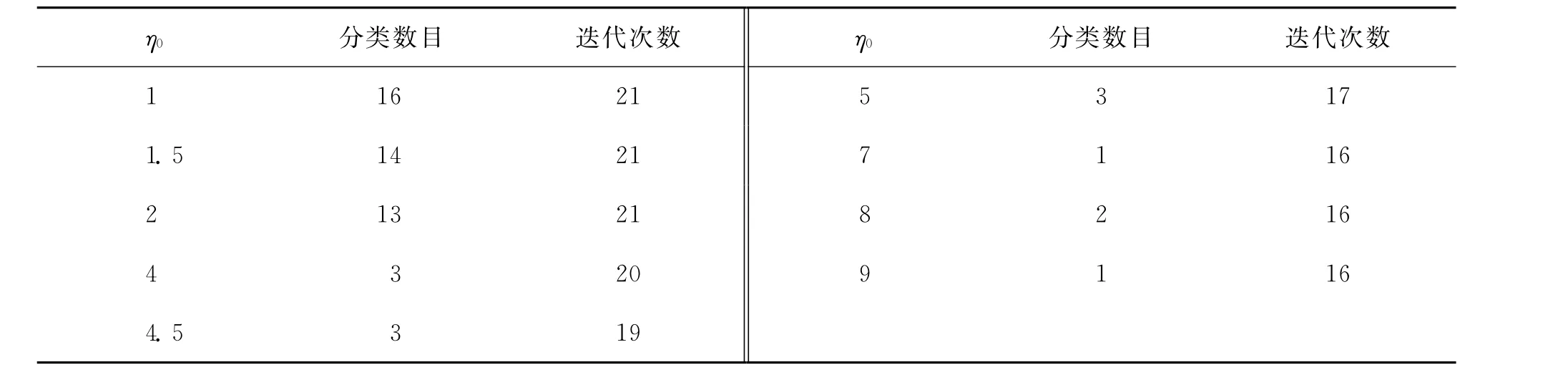
表1 η0值对分类数目和迭代次数的影响Tab.1 Influence ofη0on the number of clusters and the number of iterations

从表1中可以看出，η0的取值会影响到算法最终的聚类数目和收敛速度.Iris正确的簇数为3，但是当给定初始化最大簇数Cmax＝18和η0取值在［1，2］时，Iris数据集的簇数分别为16，14，13，说明没有得到正确的簇数，此时目标函数迭代21次.当η0取值在［4，5］时，最终聚类数为3，得到了正确的聚类结果，并且此时平均迭代次数为18左右.当η0取值在［7，9］时，算法得到的簇数是1或2，小于正确的簇数3，说明此时平衡因子的值太大使竞争超过了正常的范围，此时的迭代次数为16次.这表明当η0的值越大，算法的迭代次数越小，实验结果表明，当η0在［4，5］取值时会有比较好的聚类结果.

2.2 聚类收敛速度的比较

针对Iris，Diabetes，Wine和Data数据集对算法的聚类收敛速度进行了实验研究.在对这些数据集聚类时，Cmax分别初始化为18，13，18和18，ε＝0.001，η0＝4.图1至图4分别给出了SCAPC和M-SCAPC算法关于聚类收敛速度的实验结果.由图1可知，SCAPC算法经过24次迭代才使目标函数值稳定下来，而MSCAPC算法仅用17次迭代就稳定下来，且对于M-SCAPC算法，在第7次迭代时获得了正确簇数，而SCAPC算法在第8次得到正确的簇数.同样，由图2至图4的实验结果可以获得同样的结论.这就表明，MSCAPC算法的收敛速度要优于SCAPC算法.

2.3 点对约束与聚类性能的关系

由目标函数JM－SCAPC及算法可知，当给定样本点的标签信息和实际划分出来的类属信息不一致时，则目标函数中的惩罚项会变大，此时惩罚项会不断的被调整，从而在迭代过程中一些错误的样本点会被分到正确的类之中.为了验证这个结论，对给定的4个数据集，实验研究了点对约束数目和聚类结果的关系.针对Iris， Diabetes，Wine和Data数据集，实验中η0分别被置为4，5，5.5和6，Cmax＝18，ε＝0.001，实验结果如图5所示.

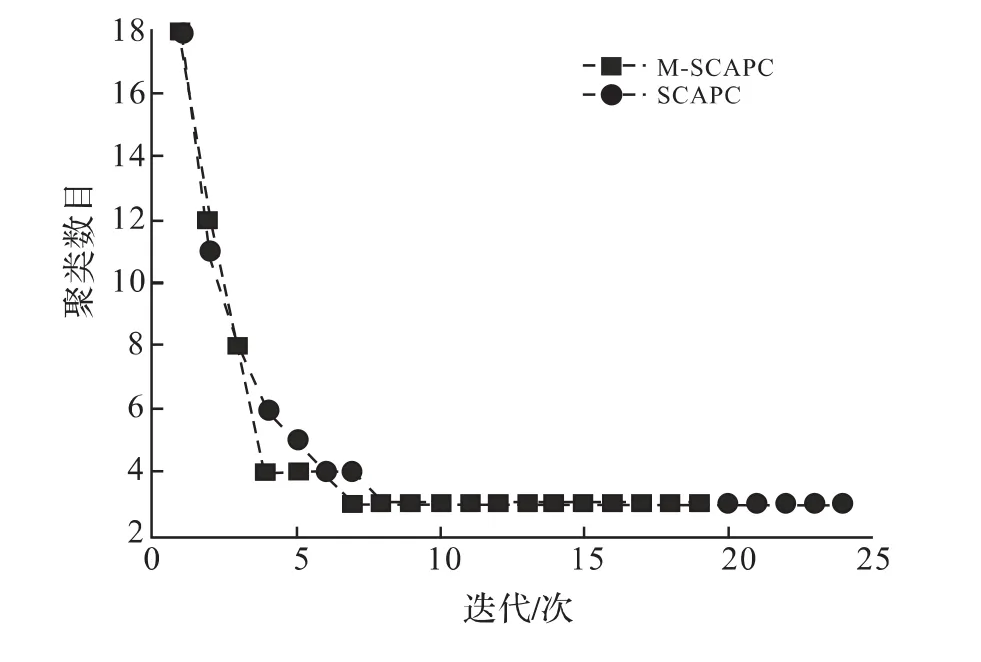
图1 SCAPC算法和M-SCAPC算法在Iris数据集上的聚类收敛速度Fig.1 Comparison with convergence speed between SCAPC and M-SCAPC on the Iris data set

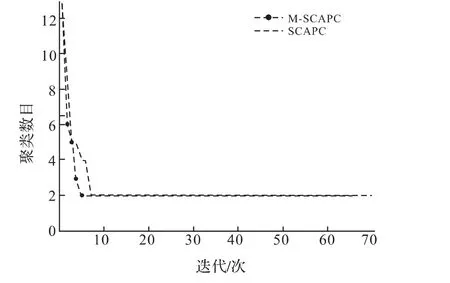
图2 SCAPC算法和M-SCAPC算法在Diabetes数据集上的聚类收敛速度Fig.2 Comparison with convergence speed betweenSCAPC and M-SCAPC on the Diabetes data set

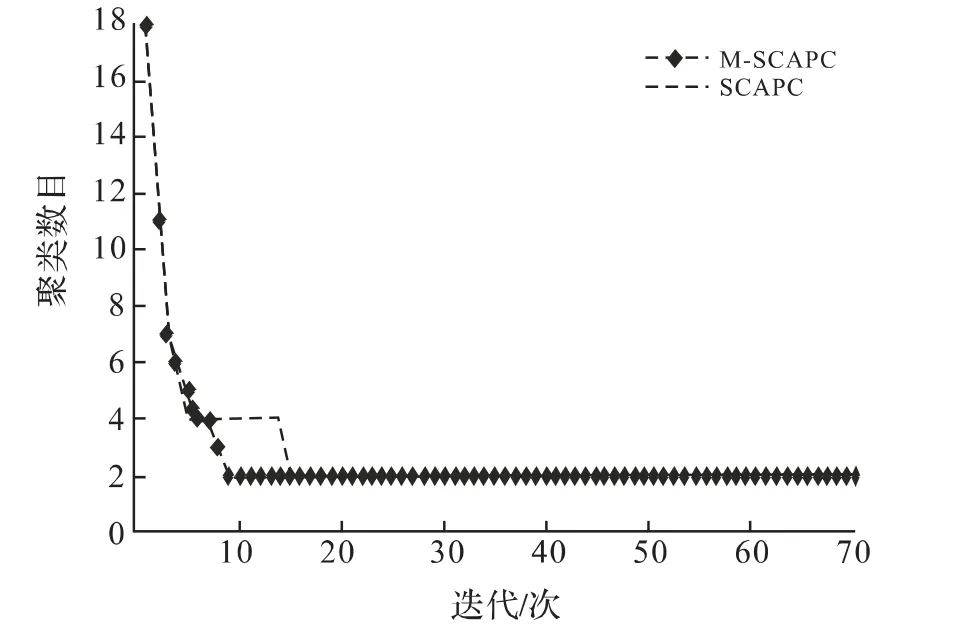
图3 SCAPC算法和M-SCAPC算法在Wine数据集上的聚类收敛速度Fig.3 Comparison with convergence speed between SCAPC and M-SCAPC on the Wine dataset

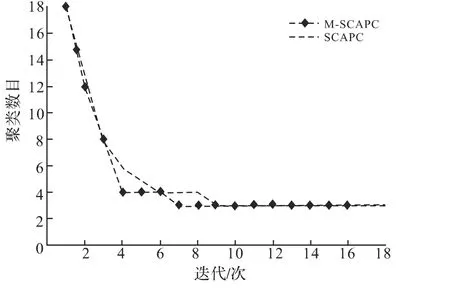
图4 SCAPC算法和M-SCAPC算法在Data数据集上的聚类收敛速度Fig.4 Comparison with convergence speed between SCAPC and M-SCAPC on the Data dataset

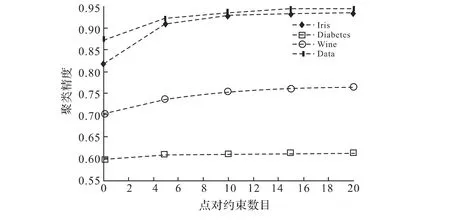
图5 不同数目的点对约束下的聚类正确率Fig.5 Clustering accuracy with different number of constraints

由图5可以看到，随着点对约束（must-link和cannot-link）数量的增加，M-SCAPC算法的正确率逐渐增高，这表明了约束惩罚项对目标函数有显著的调整作用.当点对约束数目较少时，聚类结果的正确率相对较低；当点对约束数量增加时，聚类结果的正确率有显著的提升；当点对约束数量达到一定值时，聚类结果逐渐稳定，此时，点对约束的数目对聚类结果的影响较小.

2.4 不同算法的聚类正确率比较

为了进一步验证M-SCAPC算法的有效性，选取FCM，AFCC和SCAPC算法进行了实验比较.实验中选取10个点对约束，表2给出了不同算法的实验结果.可以看出改进的M-SCAPC算法在Iris，Diabetes，Wine和Data数据集上明显提高了聚类结果的正确率，尤其是对于一些高维数据集如Diabetes和Wine获得了较好的聚类结果.

表2 不同算法的聚类结果Tab.2 Clustering results using different algorithms

3 结论

本文通过应用马氏度量且修改半监督模糊聚类算法的目标函数，得到一个改进的半监督模糊聚类算法M-SCAPC，并且针对不同的数据集Iris、Diabetes、Wine和Data进行了实验研究.实验结果表明改进的算法M-SCAPC显著地提高了聚类结果的正确率和收敛速度.另外，与聚类算法FCM，AFCC和SCAPC进行了实验比较，表明了M-SCAPC算法的有效性.

［1］ XIANG Shiming，NIE Feiping，ZHANG Changshui.Learning a Mahalanobis distance metric for data clustering a classification［J］.Pattern Recognition，2008，41（12）：3600-3612.

［2］ BAR-HILLEL A，HERTZ T，SHENTAL N，et al.Learning a Mahalanobis metric from equivalence constraints［J］.Journal of Machine Learning Research，2005，6：937 -965.

［3］ YIN Xuesong，SHU Ting，QI Huang.Semi-supervised fuzzy clustering with metric learning and entropy regularization［J］.Knowledge-Based Systems，2012，35：304-311.

［4］ YEUNG D Y，CHANG H.Extending the relevant component analysis algorithm for metric learning using both positive and negative equivalence constraints［J］.Pattern Recognition，2006，39（5）：1007-1010.

［5］ FRIGUI H，KRISHNAPURAM R.Clustering by competitive agglomeration［J］.Pattern Recognition，1997，30（7）：1109-1119.

［6］ GRIRA N，CRUCIANU M，BOUJEMAA N.Semi-supervised fuzzy clustering with pairwise constrained competitive agglomeration［Z］.IEEE International Conference on Fuzzy Systems，Reno，Nevada，USA，2005.

［7］ GRIRA N，CRUCIANU M，BOUJEMAA N.Active semi-supervised fuzzy clustering［J］.Pattern Recognition，2008，41（5）：1834 -1844.

［8］ GAO Cuifang，WU Xiaojun.A new semi-supervised clustering algorithm with pairwise constraints by competitive agglomeration［J］.Applied Soft Computing，2011，11（8）：5281-5291.

（责任编辑：孟素兰）

A semi-supervised fuzzy clustering algorithm based on pairwise constraints and Mahalanobis distance

LI Kai，WANG Liang，ZHOU Yufei
（College of Mathematics and Computer Science，Hebei University，Baoding 071002，China）

The semi-supervised fuzzy clustering based on pair-wise constraints which introduces Mahalanobis distance into SCAPC（Semi-supervised fuzzy Clustering Algorithm with Pairwise Constraints）algorithm is mainly studied.And a new semi-supervised fuzzy clustering objective function is obtained.By solving the optimization problem，a semi-supervised fuzzy clustering algorithm M-SCAPC（Modified SCAPC）based on pairwise constraints and Mahalanobis distance is proposed.And some experimental researches are conducted for M-SCAPC algorithm using the selected standard data set and the artificial data set.Besides，clustering performance on M-SCAPC algorithm are compared with that of FCM（Fuzzy C-Means），AFCC（Active Fuzzy Constrained Clustering）and SCAPC algorithms.From the results，M-SCAPC is effective in the convergence speed and the accuracy.

semi-supervised clustering；pairwise constraints；metric learning；mahalanobis distance

半监督聚类是半监督学习的一个重要研究方向，它将监督聚类和无监督聚类的优势结合起来，利用少量具有监督信息的样本和大量无标签样本进行聚类.一般来说，监督信息主要有2种形式：一种是偶对约束，例如must-link和cannot-link；另一种是直接给出样本点的分类标记信息.目前，针对这2种监督信息，研究人员提出了许多不同的半监督聚类算法，这些方法大体可以归结为2种类型：1）将监督信息引入到现有的聚类算法中，以此获得半监督聚类算法；2）利用监督信息对度量进行学习［13］.例如，Bar-Hillel等［2］利用mustlink约束通过学习马氏度量提出了一种非迭代方法RCA（relevant component analysis），之后，Yeung等［4］针对RCA方法进行了扩展研究，在该方法中同时考虑了must-link约束和cannot-link约束.对于大多数聚类算法，不论是无监督聚类和半监督聚类，在聚类时通常都需要事先指定要聚类的簇数，然而在实际问题中，这个值是很难被确定的.关于这个问题，Frigui等［5］提出了CA（competitive agglomeration）算法，主要通过竞争方法自动计算合适的聚类数目，遗憾的是该算法的聚类效果较差.为了提高聚类的性能，Grira等［67］将半监督聚类方法与CA算法进行有效的结合，提出了AFCC（active fuzzy constrained clustering）算法.鉴于AFCC算法中的偶对约束惩罚项和CA算法的目标函数在数量级上不一致，在聚类过程中可能引起样本点的隶属度调整过度问题.在2011年，Gao等［8］进一步改进了AFCC算法的目标函数，并在此基础上提出了SCAPC（semi-supervised fuzzy clustering algorithm with pairwise constraints）算法.可以看到，不论AFCC算法还是SCAPC算法，在优化问题中的目标函数都是基于欧氏距离，而欧氏距离仅对球形数据有比较好的聚类效果，对于那些非球形或者椭圆形的样本点数据，使用这些算法并不能得到较好的聚类结果.针对这种情况，本文将马氏距离引入到算法SCAPC的目标函数中，提出了一种基于马氏距离的半监督模糊聚类算法M-SCAPC（Modified SCAPC）.

TP391

A

1000-1565（2014）05-0535-06

10.3969／j.issn.1000 -1565.2014.05.016

2014-01 -09

国家自然科学基金资助项目（61375075）；河北省自然科学基金资助项目（F2012201014）

李凯（1963-），男，河北满城人，河北大学教授，博士，主要从事机器学习、数据挖掘等方向研究.E-mail：likai＠hbu.edu.cn