基于无裂纹直耳片接头接触问题的非线性分析

徐 丹，李朝光，王学强，朱亲强

（中航工业洪都，江西南昌330024）

0 引言

耳片型接头是飞机结构中常用的连接型主要构件，其使用环境较恶劣，极易造成疲劳损伤，引起失效，是飞机结构中最具断裂危险的原件之一。关于耳片损伤容限设计，需要在新结构的危险部位存在小的初始缺陷时，进行预计结构的疲劳裂纹扩展寿命和剩余强度。而在含有初始裂纹连接耳片的分析中，普偏关心的基本项目是无裂纹状态下的应力分布[1]。

无裂纹耳片结构形式虽然简单，但耳孔周围的应力状态却较复杂。耳片连接件主要通过螺栓给耳片传递载荷，随着载荷的增加，耳孔与螺栓的接触由线接触变化到半个螺栓面的接触。螺栓和耳孔内表面传力过程属于接触应力问题，是典型非线性问题，采用常规的弹性力学的解析方法很难确定边界形状及接触状态，因此对于耳孔周围的应力状态也很难分析。

目前已有一些文献[2]，给出了一些特定参数下规则的直耳片的应力强度因子。本文从有限元分析的方法出发，采用弹簧元来模拟螺栓和耳片的接触形式，调节弹簧元的接触刚度，分析计算了耳片的孔边应力。给出了规律性的结果，为含初始裂纹连接耳片分析提供了探讨性研究，为耳片损伤容限设计做铺垫。

1 有限元模型及方法

接触问题属于典型非线性问题，接触问题所特有的接触截面非线性有两个方面的原因[3]：其一，接触区域截面大小和位置以及接触状态不仅事先都是未知的，而且随着时间的变化，需要在求解过程中确定；其二，接触条件的非线性，即接触物体的不可相互侵入、接触力的法向分量只能是压力、切向接触的摩擦条件。

接触问题的关键与难点在于接触界面条件的定义。弹性接触理论方法都是通过一些简单的数学公式来解决接触问题，对于一些接触形状复杂的问题很难用解析公式表示。有限元法将接触截面划分为一系列的单元，单元之间以节点连接。这些单元结构形状简单，易于用平衡关系或能量关系建立节点之间的边界条件，为求解工程中的复杂接触问题提供了有利手段。

1.1 有限元模型

为了使结构具有代表性，模型选择了飞机耳片接头中典型对称的直耳片进行分析。螺栓和耳片均采用六面体单元，分别取不同的R0/Ri值，螺栓载荷作用在0°方向。本文给定耳片与螺栓的初始间隙均为0.01mm。

1.2 接触边界处理

采用弹簧元来处理螺栓和耳片接触点间的位移协调问题，假设螺栓和耳片之间是光滑净配合，不考虑摩擦力。

借助于赋予弹簧元在压缩时很高的刚度和在拉伸时很低的刚度，通过迭代，使接触点对之间满足法向接触协调条件。

假设任一可能接触点对为i、j[4]，见图1，法向位移分别为δni、δnj，接触间隙为ΔXij，初始间隙为ΔX0ij，法向节点弹簧力为Pi,则接触判定条件表示为：

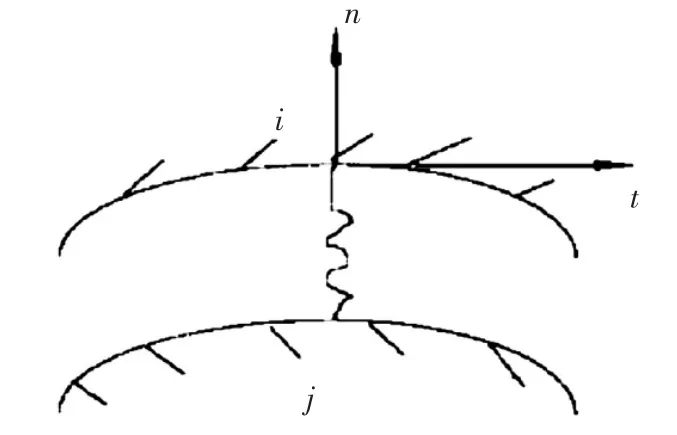
图1 接触点对示意图

通过接触的判定条件，判别耳片与螺栓的接触面。由于模型选择在0°方向加载，接触面积为耳片与螺栓接触的半圆周上。因此有限元模型中定义了半个圆周上的弹簧元。

1.3 耳片外载荷分配

耳片通过与螺栓的相互挤压来传递载荷，应力分析时，假设载荷和应力沿耳片厚度方向保持不变，载荷按余弦规律分布[2]在螺栓和耳片相互作用的挤压面上，见图2。

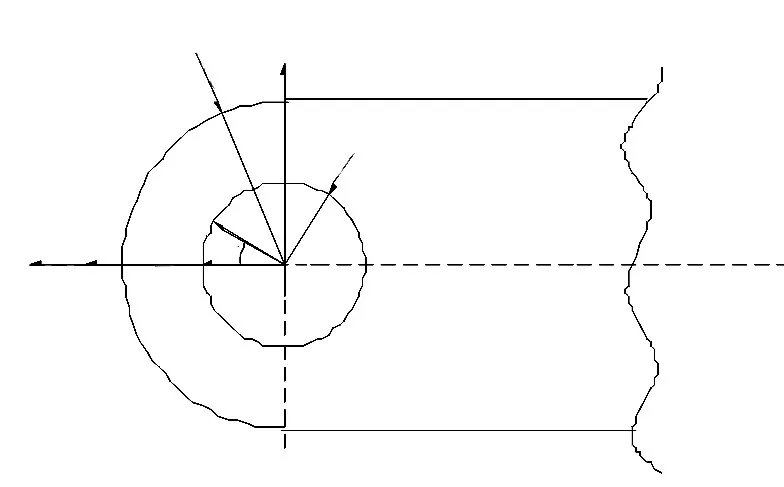
图2 沿耳孔挤压面上的载荷示意图

挤压面上i的径向载荷为：

径向沿x,y方向的载荷为：

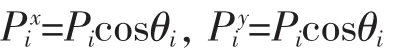
因此，沿0°加载的总合力为：

式中：Pi为外载荷P作用线通过挤压面上A单元分配的载荷；θi为耳孔挤压面上i点偏离外载荷方向的角度。

因此可根据外载荷来获得沿耳孔挤压面上每个弹簧元分配的载荷，进而调节弹簧元的刚度来协调位移。

1.4 弹簧元刚度的定义

假设螺栓移动微小位移ΔX,即整个耳片向载荷加载的方向平移ΔX，见图3。那么在螺栓和耳片相互作用的挤压面i点的径向位移为：

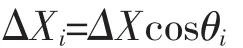
则，在螺栓与耳片相互作用的挤压面i上的弹簧元刚度应为：

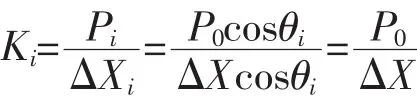
2 有限元计算结果及分析

2.1 应力集中系数的理论算法

根据文献[2]提供直耳片孔边应力集中系数的计算的经验公式为：

注：Kt为孔边最大切向应力按平均挤压应力正则化所得。

依据上式，现给出不同R0/Ri情况下的孔边应力集中系数，见表1。

表1 不同耳片对应的应力集中系数

2.2 有限元计算结果与理论结果比较

选取三种不同半径的接头耳片进行计算分析，三种计算模型的几何尺寸如表2所示。

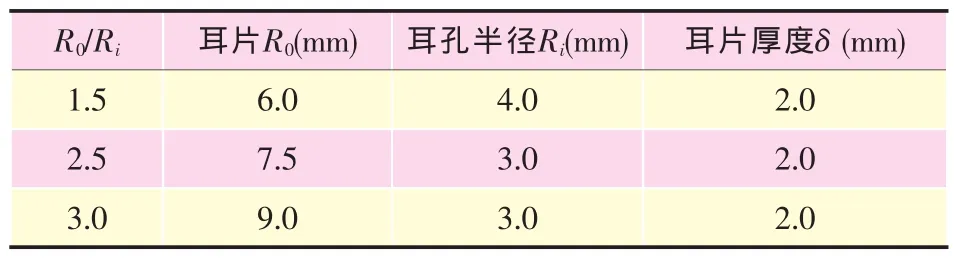
表2 两种情况计算模型几何参数

计算结果见图3、图4、图5，图中所示为最大剪切应力云图。

图3 R0/Ri=1.5有限元应力云图

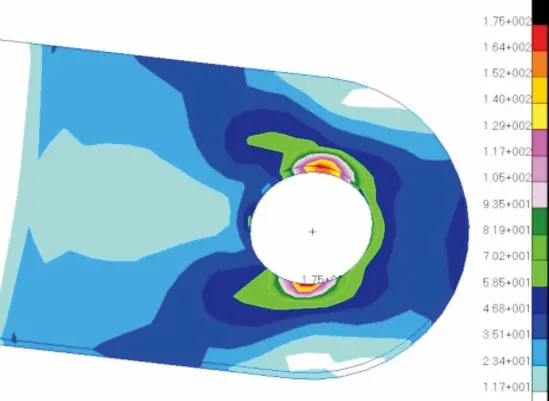
图4 R0/Ri=2.5有限元应力云图

图5 R0/Ri=3有限元应力云图

比较有限元计算结果与理论计算结果对应的孔边应力集中系数，见表3。

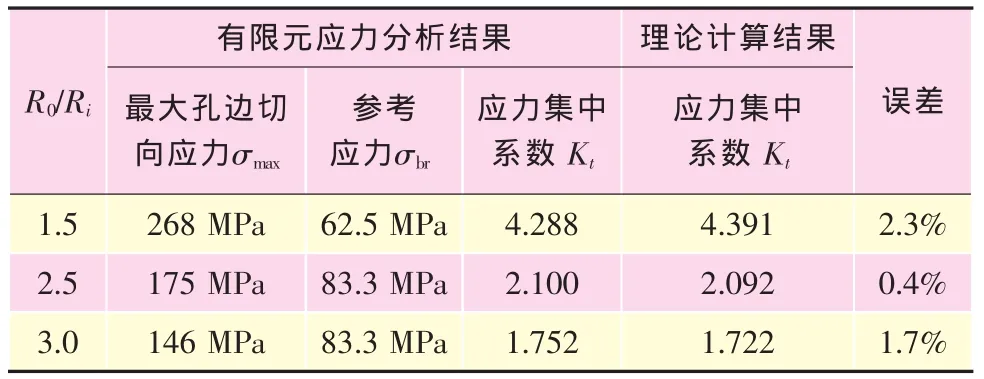
表3 有限元应力分析结果与理论计算结果比较

从表3中数据可以看出：有限元应力分析结果与理论计算的结果相近，说明运用弹簧元能够较真实地模拟耳片与螺栓之间的接触问题。

2.3 几何尺寸对应力集中系数的影响

1）相同 R0/Ri情况比较

相同R0/Ri情况下两种耳片的几何参数与对应的计算结果见表4。

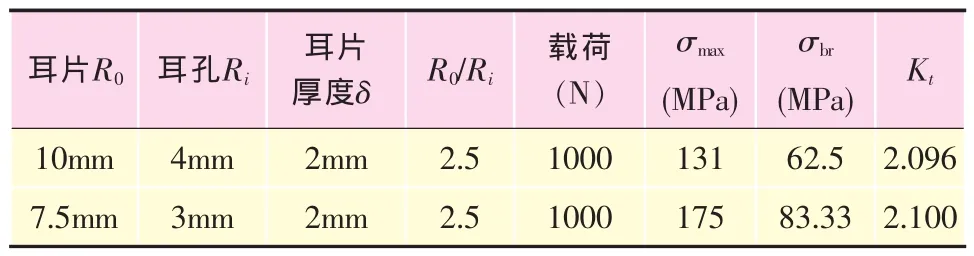
表4 两种耳片几何参数及加载结果比较

根据表4比较结果可以看出，具有相同值的不同耳片，其孔边最大剪切应力集中系数一致。

2）厚度对应力集中系数的影响

根据表5比较结果可以看出，不同厚度耳片，其孔边最大剪切应力集中系数趋于一致，说明耳片的厚度对耳片的应力集中系数不影响。

表5 两种耳片几何参数及加载结果比较

3 结语

1）本文采用弹簧元处理螺栓和耳片接触点间的位移协调问题。通过外载荷获得沿耳孔挤压面上每个弹簧元分配的载荷，调节弹簧元的刚度来协调位移。

2）通过有限元方法建立了三种不同大小的耳片，计算得到危险点的应力集中系数与理论计算结果较一致的应力集中系数和耳片应力分布情况，能够较真实地模拟无裂纹直耳片与螺栓之间的接触问题。

3）具有相同值的不同耳片，有相同的应力集中系数和应力分布情况；耳片厚度不影响耳片的应力集中系数，与理论经验公式相符合。

[1]吴富民.结构疲劳强度[M].西安：西北工业大学出版社，1985.

[2]樊东黎.热处理工程师手册.北京：机械工业出版社，2004,9.

[3]飞机结构强度研究所.航空结构连接件疲劳分析手册.南京：飞机结构强度研究所,1985.

[4]黄其青.对称与非对称斜削耳片危险部位及应力强度因子的有限元分析.航空学报,1998,19(4).