基于多元GARCH模型的可转换债券市场与股票市场的波动关系研究*

马瑛琪，周远翔，张 晶

（1.安徽财经大学金融学院，安徽蚌埠 233030；

2.安徽财经大学统计与应用数学学院，安徽蚌埠 233030）

基于多元GARCH模型的可转换债券市场与股票市场的波动关系研究*

马瑛琪1，周远翔2，张 晶1

（1.安徽财经大学金融学院，安徽蚌埠 233030；

2.安徽财经大学统计与应用数学学院，安徽蚌埠 233030）

可转换债券作为一种混合型的金融衍生品，已经成为金融市场中重要的组成成分，并且其市场与股票市场之间又是互相影响的，它们的共同发展对金融市场的繁荣和企业竞争力的提高方面起到了积极的推动作用.因此，对可转债市场与股票市场之间关系的实证研究具有一定的理论与现实意义.基于上证指数（000001）与上证转债指数（000139），运用BEKK形式的多元GARCH模型来实证研究可转债市场与股票市场之间的波动关系及其溢出效应.实证结果发现，这两个市场之间有正相关的关系，并且存在双向的波动溢出效应.

可转债市场；多元GARCH模型；收益率波动；波动溢出效应

近几年，可转换债券市场的发展，在一定程度上解决了我国证券市场上存在的股权融资比例过高，债券类和权益类金融产品缺乏创新等问题.又可转债具有债性和股性以及看涨期权等特点，灵活的选择权再加上融资成本低和风险规避功能，使其越来越受到投资者、上市公司的关注和热捧.因此，可转债势必对国家经济的发展和金融市场的稳定产生重要的影响.从长远来看，随着我国资本市场的逐步完善、金融自由化的发展、市场间信息传递速度的加快以及投资者套利行为的影响，金融市场之间必然会呈现出显著的互动关系，可转债市场与股票市场之间自然也不例外.因此，研究可转债市场与股票市场的波动特征及其两者之间的溢出效应，能够促进证券市场的稳定，同时可为投资者构建跨市场投资组合、分散风险和融资者进行融资提供指导.

1 文献综述

衍生金融产品与其标的资产之间，以及不同的衍生品之间在价格上存在一定的关系，国外对此进行了大量的研究.根据B－S期权定价模型的原理，期权价格与标的股票价格之间有一定的关系，并检验了CBOE市场的有效性［1］；通过对芝加哥证券交易所中进行交易的股票看涨和看跌期权进行研究，也验证了衍生产品与标的资产之间的关系以及期权平价的关系［2］；从股票以及期权市场的交易量上看，标的股票的交易要比看涨期权的交易滞后一天［3］.此外，国外学者还对期货做了研究，比如股指期货价格与现货价格之间的关系，进一步分析了市场的有效性［4］.

国內的衍生金融产品不多，而且可转债发展的时间并不长，大部分人对其衍生产品的特性还不熟悉.国内学者对可转债的研究主要集中在对其定价上，如我国沪深两市的可转债是在考虑其条款设计特殊性的基础上进行定价的［5］.但是对可转债与标的股票之间关系的研究不多，如根据无风险套利原理研究可转换债券价格与基础股价之间的关系，以此来检验市场的有效性［6］.运用误差修正模型得到两者之间有协整关系，不过其传导存在时滞效应［7］.关于可转债市场与股票市场的联动关系，一方面研究发现两者之间存在长期稳定的协整关系［8］，并且两个市场有相似的波动特征和收益率变化程度［9］；另一方面采用Granger因果关系检验和方差分解的方法也得出两市场间有显著的联动关系［10］.如果把利率考虑在内，运用VAR－（BV）EGARCH模型发现两者之间存在波动溢出效应［11］.其他学者是基于GARCH模型也对此进行计量研究［12－14］.

综合以上分析，多元GARCH模型可以更好地刻画市场之间的波动及风险传递.目前，相关研究很少，因此为了更深刻地了解可转债市场与股票市场之间的关系，运用多元GARCH模型来求出两市场间的相关系数及其波动溢出效应，进一步分析两市场的动态传导关系，以此给投资者提供建议.

2 理论背景

可转债市场与股票市场是资本市场的两个重要子市场，它们同时受到国家宏观经济政策、公司的基本情况以及市场管理制度等因素的影响，再加上投资者在两个市场上追逐套利的行为和投资资金流动的加快，使得可转债市场与股票市场具有很强的关联性.

可转债可在转股期内根据转换比例和转股价格转换成相应公司的股票.直观上讲，它可以被看成在债券的基础上附加了一个看涨期权，这就决定了可转债价格随着标的股价的变动而变动，因为转股价值与股票价格之间呈正相关的关系，股价上升会使转股价值增加，进一步推动可转债价格上升，尤其当股价超过转股价格后，差额越大，可转债持有人则越愿意转股并抛售股票来获取套利收益，此时可转债表现的是股性，这说明可转债价格与股价有着高度的敏感性，可转债与基础股票的关系紧密.同时，可转债价格的变动也会通过认股权证影响股价的波动.

3 研究设计

3.1 研究假设

由于可转债可以看作把该公司股票的看涨期权内嵌于一张普通债券中，所以我们对可转债与股票之间的关系作出如下假设：

（1）股票市场的走势指引着可转债市场，前者对后者有预测作用；

（2）可转债市场与股票市场的收益率之间的波动存在相关关系；

（3）股市与可转债市场间有波动溢出效应，而且是双向的.

3.2 样本数据说明

样本数据均来自于大智慧软件和Wind金融资讯终端.为了反映沪市可转债的总体情况，我们选取上证转债指数（000139）为研究指标，这是因为其样本由在沪市上市的可转债构成.又上证指数（000001）可以综合反映上交所股票的走势，再加上发行可转债公司的股票几乎全为上证指数的成分股，因此，研究上交所的可转债市场与股票市场的波动关系，选取上证转债指数与上证指数具有很好的代表性和合理性.为了统一时间口径，样本日期选取2004年1月8日至2013年12月31日，取指数的日收盘价，得到2421个数据.

本文所考察的时间序列是指数收益率序列，所以首先对原始数据进行处理，我们定义指数日收益率Rt＝ln ptln pt－1，其中pt是指数的日收盘价.用rp代表上证指数日收益率，rz代表可转债指数日收益率，将其收益率序列在Eviews 6.0软件中进行处理.

3.3 分析方法

一般假设股价或指数的运动是随机游走的，但其收益率序列是平稳的，且股价的走势呈现出尖峰粗尾现象以及其收益率的波动具有集聚性，故我们选择GARCH类模型进行分析.

一元GARCH模型是在ARCH模型的基础上得到的，弥补了ARCH模型的不足.标准的GARCH模型为：

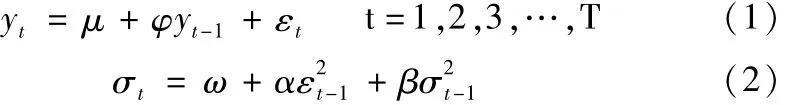
其中，（1）为均值方程，（2）为条件方差方程，ε2t－1是ARCH项，σ2t－1是GARCH项，即为上一期的预测方差.

多元GARCH模型是在一元GARCH模型的基础上发展而来的，但相比传统的一元GARCH模型只能刻画单一金融资产风险的纵向传递，多元GARCH模型不仅能刻画多个金融资产沿时间方向的波动集聚，还能有效捕捉不同金融资产之间的风险交叉传递.本文采用的模型是BEKK形式的多元GARCH模型.BEKK模型最初由Baba等提出的，它可以在比较弱的情况下保证协方差矩阵的正定性，而且所需估计的参数相对较少，是一个比较实用且方便的表达式.本文研究的

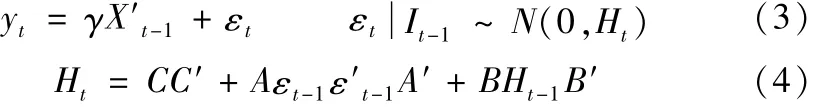
其中，（3）为均值方程，（4）为BEKK形式的多元GARCH形式的方差方程.yt是2×1维的收益率向量，Xt是1×（k＋1）维解释变量向量，γ是2×（k＋1）维系数矩阵，C为下三角常数矩阵，A代表ARCH项的系数矩阵，B代表GARCH项的系数矩阵，Ht为2×2维对称矩阵，表示条件残差在t时刻的方差协方差矩阵，其表达式为：是可转债市场与股票市场这两个市场的波动关系，所用到的是二元BEKK模型，该模型的设定形式为：

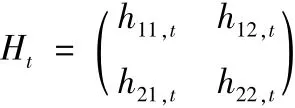
4 实证分析

4.1 数据的基本分析与诊断性检验

4.1.1 可转债指数收益率与股指收益率的波动

为了考察可转债市场与股票市场的波动特征，首先对其收益率序列进行描述，作上证指数收益率和上证转债指数收益率图，如图1，2所示.

图1 上证指数收益率图

从图1，2可知，两个收益率的波动有聚类的现象，在一些时间内较平稳，一些时间内较剧烈，说明其可能具有条件异方差.

4.1.2 格兰杰因果关系检验

通过ADF方法对上证指数收益率和可转债指数收益率序列的平稳性进行检验之后，对它们进行Granger因果关系检验，结果如表1所示.

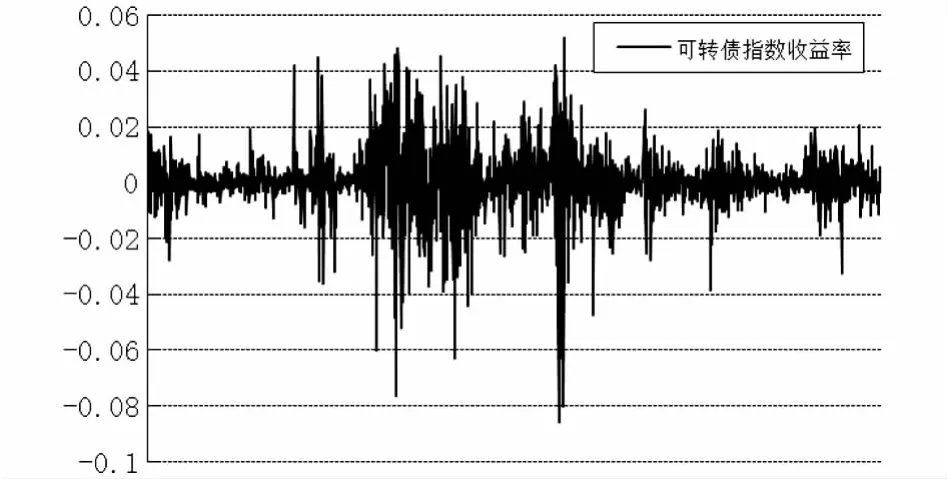
图2 上证转债指数收益率图

表1 Granger因果关系检验结果

从表1可以看出，由F统计量的伴随概率可知，0.12346＞0.05＞0.01335，rp是rz的格兰杰原因，而rz不是rp的格兰杰原因，这说明股票市场引导着可转债市场的走势，也明确了股票市场的基础导向作用.

4.1.3 ARCH效应检验

检验指数收益率序列是否存在ARCH效应，对收益率序列均值方程的残差进行ARCH－LM检验，检验结果如表2.

表2 指数收益率序列的ARCH效应检验结果

从表2可知，两个收益率序列的P值均为0，说明rz和rp序列的残差存在显著的ARCH效应，故可用GARCH模型进行进一步建模分析.

4.2 BEKK形式的多元GARCH模型的建立

分别对可转债指数收益率和上证指数收益率序列建立均值方程和方差方程，估计结果如下所示：可转债指数收益率的GARCH模型：均值方程：

从（6）式和（8）式中可以看出，条件方差方程中的ARCH项和GARCH项都是高度显著的，说明收益率序列的波动具有集聚性.两市场中的ARCH项和GARCH项系数之和均为0.99，小于1，满足参数的约束条件，这表明过去的波动对预期的影响力是越来越弱的.又由于其系数之和与1高度接近，这说明条件方差受到持久的冲击.

继续利用多元GARCH模型分析两个市场之间的波动反馈关系，研究它们之间是否存在动态波动率依赖.因此，利用BHHH算法对可转债指数收益率和上证指数收益率序列建立BEKK形式的方差方程，考虑到本文的目的是考察方差间的影响，所以只给出了方差方程的估计结果，如（8）式所示：

从未对参数施加任何限制的BEKK模型的估计结果（9）式看，方差方程的ARCH项系数矩阵A和GARCH项系数矩阵B的对角元素α11，α22，β11，β22均显著不等于零，说明可转债市场和股票市场的波动均受自身以往波动的影响，波动集聚性显著.

4.3 股票市场和可转债市场的波动溢出效应研究

所谓波动溢出效应是指一个市场的波动不仅对自身未来有影响，还可能对其它市场未来的波动产生影响，其实是“金融传染”的表现，反映的是收益率条件二阶矩之间的格兰杰因果关系.在前面研究的基础上，从GARCH模型的残差项中分别提取条件方差VP（股票市场）和VZ（可转债市场），用以代表股市和可转债市场的波动性.在Eviews6.0软件中进行处理，首先计算得出两者之间的相关系数为0.5，说明股票市场和可转债市场的波动呈现出正相关关系，两市同时大起大落.然后考察两市波动的Granger因果关系，其检验结果表3所示.

表3 两市波动的Granger因果关系检验结果

从表3可以看出，我们均可以拒绝原假设，即VZ是VP的格兰杰原因，并且VP也是VZ的格兰杰原因，这说明了股票市场和可转债市场的波动之间存在双向的溢出效应，即股票市场的波动会导致可转债市场的波动，同时可转债市场的波动也会导致股票市场的波动.波动溢出效应的检验结果与通过Wald检验的结果相一致.

4.4 实证结果分析

本文以上证转债指数和上证指数为指标，运用GARCH模型实证探讨了可转债市场与股票市场之间的波动关系，基于实证分析，我们得出以下结论：

第一，由股票市场与可转债市场的指数收益率序列的格兰杰因果关系检验结果可知，股票市场的走势引导着可转债市场，这是因为，股票市场具有相对完善的信息传递机制，这使得股价的轻微变动便可通过转股价值对可转债价格产生影响.

第二，由股票市场和可转债市场的BEKK模型可知，可转债市场和股票市场的收益率序列均受自身以往波动的影响，但前者的波动幅度要小于后者，这是由可转债本身所具有的特性决定的.

第三，由实证研究的第三部分可知，可转债市场与股票市场之间存在双向的波动溢出效应，这是由它们之间的本质联系所导致的.因为可转债具有债权和看涨期权的特点，其价格的波动肯定会通过其期权的特性影响股票市场.反之，股市通过其价格的波动，使其转股价值发生变化，影响投资者的决策，进而影响可转债的价格，传递到可转债市场.此外，投机者在两市场间的套利也促进了两者之间的波动传递.

5 结语

可转换债券作为一种新兴的金融衍生产品，在我国的发展还不完善，市场规模还比较小，但随着可转债的种类和数量日渐丰富，股票市场和可转债市场间的动态传导将会更加紧密.因此，国家在制定相关政策时，应充分考虑可转债市场与股票市场的波动特征及其风险传递，促进可转债市场与股票市场的协调发展.同时，投资者在进行投资决策时，也应充分了解可转债市场与股票市场的波动溢出效应，从而构建合理的投资组合，以达到分散投资风险的目的.

［1］Galai D.Tests ofmarket efficiency of the Chicago board options exchange［J］.Journal of Business，1977，（2）：167－197.

［2］Klemkosky R C，Resnick B G.Put-call parity and market efficiency［J］.The Journal of Finance，1979，（5）：1141－1155.

［3］Anthony JH.The interrelation of stock and optionsmarket tradingvolume data［J］.The Journal of Finance，1988，（4）：949－964.

［4］Peters E.The growing efficiency of index futuresmarkets［J］.The Journal of Portfolio Management，1993，（4）：52－56.

［5］赖其男，姚长辉，王志诚.关于我国可转换债券定价的实证研究［J］.金融研究，2005，（9）：105－121.

［6］黄建兵.中国的可转换债券与市场价格有效性研究［J］.系统工程理论方法应用，2002，（1）：63－67.

［7］吴谦.可转债价格与股票价格动态传导关系实证研究——基于多变量协整方法和非对称误差修正模型的检验分析［J］.财经研究，2007，（5）：134－142.

［8］张秀艳，张敏，闵丹.我国可转换债券市场与股票市场动态传导关系实证研究［J］.当代经济研究，2009，（8）：52－55.

［9］张秀艳，张敏.可转换债券市场与股票市场的波动关系——基于二元GARCH模型的实证研究［J］.吉林大学学报，2009，（4）：133－140.

［10］张苏凤.中国可转债市场与股票市场间联动关系研究［D］.西安：陕西师范大学硕士学位论文，2011.

［11］胡秋灵，张苏凤，王宁.可转债市场与股票市场间的溢出效应研究［J］.北京理工大学学报（社会科学版），2011，（3）：55－59.

［12］何启志，范从来.中国通货膨胀的动态特征研究［J］.经济研究，2011，（7）：91－101.

［13］He Q，Shen H，Tong Z.Investigation of inflation forecasting［J］. Applied Mathematics＆Information Sciences，2012，（3）：649－655.

［14］何启志.国际因素有助于中国通货膨胀水平预测吗［J］.管理世界，2012，（11）：172－173.

（责任编校：晴川）

Research on the Volatility Relation Between Convertible Bond Market and Stock M arket Based on GARCH M odel

MA Yingqi1，ZHOU Yuanxiang2，ZHANG Jing1
（1.School of Finance，Anhui University of Finance&Economics，Bengbu Anhui233030，China；2.School of Statistics and Applied Mathematics，Anhui University of Finance and Economics，Bengbu Anhui233030，China）

Convertible bond has become an important partof financialmarketas amix－typed financial derivative and itsmarket is regarded as an importantmarket segmentof capitalmarketalong with stock market.The twomarkets have influence on each other，their mutual development can promote the prosperity of financialmarket and improve the competitiveness of corporations.Therefore，researches on the relation between convertible bond and stock are of particular empirical and practical significance.Based on Shanghai composite index（000001）and Shanghai bond index（000139），this article conducts an empirical study on the volatility relationship between convertible bond market and stock market aswell as the spillover effect by usingmultivariate GARCH model.The empirical results find that there are positive correlation between the twomarkets and bidirectional volatility spillover effect.

convertible bond market；multivariate GARCH model；yields fluctuate；volatility spillover effects

F830.91

A

1008－4681（2014）05－0096－04

2014－08－10

马瑛琪（1992－），女，安徽宿州人，安徽财经大学金融学院硕士生.研究方向：宏观金融、金融工程.