石墨烯量子点二聚物的等离激元激发

尹海峰, 张 红, 刘丹丹

(1.凯里学院物理与电子工程学院,贵州凯里556011； 2.四川大学物理科学与技术学院,四川成都610065；3.中原工学院理学院,河南郑州450000)

自2004年石墨烯的发现以来,石墨烯的可控制备、新奇物理效性的揭示,以及它们的新应用探索等研究内容一直备受关注[1-2],其中,石墨烯等离激元方面的研究尤其受到重视[3].与金属相比,通过外加静电场等方法,可以有效、方便地调控石墨烯中的等离激元[3].石墨烯光子器件,可以从太赫兹波段到可见光不同频率范围内工作.同时,它还可以把等离激元共振局限于空间很小的区域.利用这一特性,石墨烯有望应用于变换光学,并最终有望应用于光计算和超高速信息处理等领域中的全光逻辑门器件[4].人们目前正在积极探究石墨烯等离激元的共振机制[3],包括用半经验理论对纯石墨烯纳米带等离激元引起的空间局域电场增加的研究[5],经典的电磁理论对纯石墨烯纳米带之间表面等离激元耦合特性的研究等[6-7].由于量子尺寸效应,同宏观二维石墨烯相比,石墨烯量子点具有不一样的光电特性.已有研究表明,边界构型[8]和量子点尺寸[9]对石墨烯量子点光电特性有较大影响.大部分吸收光谱峰对应的共振能量,随着石墨烯量子点的平均尺度增加时,发生单调降低；而对于可见光范围的光谱,在量子点尺度增加到17 nm时有一个最小值[9].理论上,基于含时密度泛函理论,对于石墨烯量子点等离激元激发的研究表明[10]:由于量子点的尺寸和量子受限效应,在低能共振区,石墨烯量子点的光谱线发生展宽和劈裂.石墨烯量子点的等离激元激发依赖于边界的构型.沿矩形石墨烯量子点扶手椅边界方向激发时,低能共振区光谱线发生较大的展宽.此外,对称性对于石墨烯量子点的等离激元激发也起着重要的作用.沿六角石墨烯量子点所在平面不同方向激发时,吸收光谱线的线形和各吸收峰的强度基本相同.目前,实验上已经可以制造出不同形状和掺杂的石墨烯量子点[11-15].

纳米颗粒对即量子点二聚物,对量子点二聚物等离激元的研究有助于理解更复杂的量子点之间等离激元的杂化机理.作为一般的特征,文献[16-18]的研究发现金属量子点二聚物间存在3种截然不同的相互作用区.当量子点之间的间距较大,二聚物在外场的作用下发生等离激元共振时,由于量子点之间的势垒较大,2个量子点仍然保持电中性.二聚物中的等离激元共振能量点随着量子点间距的减小,发生单调的红移.该相互作用区可以称为经典作用区.当量子点之间的间距进一步减小,在经典和量子的交叉区域,由于2个量子点间的势垒降低了,电子可以较容易地隧穿过势垒,在2个量子点间来回运动,量子效应开始发挥作用.当2个金属量子点之间的间隙只有几埃时,在量子点二聚物中电荷转移等离激元激发模式将会形成[16].该等离激元共振模式随着间隙的进一步减小发生蓝移.由于量子点的等离激元激发特性依赖于量子点的材料和形状,因此人们开始研究不同形状和材料的量子点二聚物中表面等离激元的特征[19].到目前为止,还未公开发表关于小尺度石墨烯量子点二聚物等离激元激发的研究结果,所以本文对小尺度石墨烯量子点二聚物的等离激元激发特性进行了理论研究.采用含时密度泛函理论,主要探究随着间隙改变时,小尺度石墨烯量子点二聚物等离激元激发演变的规律.

1 计算方法

采用含时密度泛函理论计算石墨烯量子点二聚物的吸收光谱,具体是由OCTOPUS软件来实现[20].与密度泛函理论不同[21-22],含时密度泛函理论计算吸收光谱时,体系的运动方程是电子波函数ψ(r,t)服从的含时Kohn-Sham方程[20]

其中,n为电子密度,νHartree为 Hartree 势,νlaser为作用于体系的外场.在计算中,采用Troullier-Martins形式的模守恒赝势.对于交换关联势νxc,采用局域密度近似(LDA)即

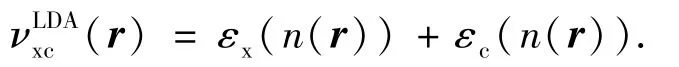
εx和εc分别为每个电子的交换和关联能,只依赖于r点处的电子密度,等于电子密度为n(r)的均匀电子气的局域交换关联能.在计算中,采用文献[20]提出的具体形式.在激发态计算中,采用绝热的LDA,νxc(r,t)=νxc(n(r,t)),交换关联势只依赖于时刻t的电子密度.

在团簇的基态计算得到电子的占据态信息后,可以通过时间演化波函数的方法来计算电子的激发态.在t=0时刻,使所有波函数有个瞬时的相位移动[23]

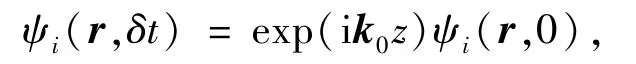
其中,k0为沿z方向所加的微扰外场动量.这相当于加E(t)=k0δ(t)的微扰外场.然后,Kohn-Sham波函数进行时间演化,可以得到含时偶极距d(t).通过对偶极距求傅立叶变换得到动态极化率α(ω),吸收光谱可以用偶极子强度函数S(ω)来表示,它与极化率的关系为

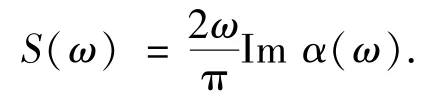
模拟时在每个原子上构建一个球,球的半径为0.8 nm,模拟空间为每个原子周围空间的并集.在模拟盒子内使用间距为0.03 nm的均匀格点.时间演化步长为3.3×10-18s,电子波函数的演化总时间为1.98×10-14s.石墨烯边界处碳原子的悬挂键用氢原子进行饱和.此外,还计算了通过石墨烯量子点二聚物间隙处的电流,计算公式为

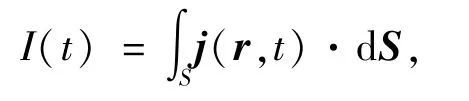
其中,S为间隙处电流通过的一个面,电流密度为

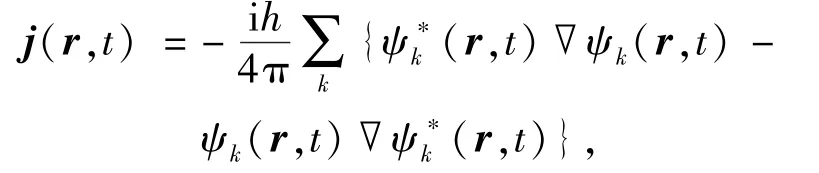
依赖于共振频率的电流大小(对电流在某些共振频率做傅立叶变换)公式为

2 结果与讨论

采用笛卡尔直角坐标系,石墨烯量子点位于XY平面内.对于具有Z字型边界的六角形石墨烯量子点,有2条边平行于Y坐标轴,如图1所示.对于矩形石墨烯量子点,其Z字型边界平行于Y坐标轴,如图2所示.主要讨论沿石墨烯量子点所在的平面方向,体系低能共振区的等离激元激发特性.

2.1 六角石墨烯量子点二聚物的等离激元激发图1给出了沿X轴方向,六角石墨烯量子点和六角石墨烯量子点二聚物的吸收光谱.从上向下,六角石墨烯量子点二聚物的间隙分别为0.8、0.4和0.1 nm.图1为六角石墨烯量子点和六角石墨烯量子点二聚物的结构示意图.对于尺度较小的六角石墨烯量子点,沿石墨烯量子点所在的平面方向,体系中仍有2个主要的等离激元共振带[10],其中,一个等离激元共振带位于能量点16 eV附近,称为π+σ等离激元；另一个等离激元共振带位于能量点5 eV附近,称为π等离激元.同较大尺度的六角石墨烯量子点相比[10],体系中主要的低能共振吸收峰发生了蓝移,分别位于3.69和6 eV.这和已有的实验研究结果一致,随着石墨烯尺寸的减小,低能区吸收光谱峰对应的共振能量单调增加[24].当间隙d比较大时,2个六角石墨烯量子点之间的相互作用是电容性的,没有电子可以穿过量子点之间的势垒.当2个六角石墨烯量子点之间的间隙d=0.8 nm时,其光谱主要的低能吸收峰分别位于3.68和5.98 eV.该结果表明,当2个六角石墨烯量子点靠近,通过电容性的相互作用时,二聚物低能共振区中主要的等离激元共振能量随着间距的减小发生了红移,即低能区主要的π等离激元共振模式随着间距的减小发生了红移.这种结果和J.Zuloaga等[16]对于金属量子点二聚物的研究结论一样.他们也发现当2个量子点之间的距离较大、在经典相互作用区时,二聚物的等离激元共振能量点随着间距的减小发生红移.在低能共振区,电容性相互作用时,石墨烯量子点二聚物光谱的线形和单个石墨烯量子点光谱的线形一样,并且石墨烯量子点二聚物吸收峰的强度约等于单个石墨烯量子点相应吸收峰强度的两倍.当2个六角石墨烯量子点之间的距离进一步减小时,量子点间的势垒降低,电子可以隧穿过势垒,在2个量子点之间运动.与金属量子点二聚物不同,随着间隙的减小,虽然在低能共振区,六角石墨烯量子点二聚物光谱吸收峰的强度进一步增加了,但是光谱的线形没有发生变化[14]；并且,随着间隙的继续减小,低能共振区的吸收光谱没有发生蓝移,而是进一步发生了红移.比如,当间隙d=0.1 nm时,其光谱主要的低能吸收峰分别位于3.62和5.88 eV,即随着间隙的减小、量子点之间势垒的降低,电子可以隧穿过势垒在2个量子点之间运动,在低能共振区,六角石墨烯量子点二聚物中,电容性耦合的等离激元共振模式虽然发生了改变,但共振能量仍然在3.68和5.98 eV附近；六角石墨烯量子点等离激元共振模式之间的耦合较弱.

为了更进一步说明六角石墨烯量子点二聚物低能等离激元共振的物理机制,我们计算了每个共振频率所对应的诱导电荷密度分布和依赖于共振频率的电流大小.图3给出了依赖于共振频率的电流随着2个六角石墨烯量子点之间的间隙d的演变过程.计算中电流通过的平面位于2个六角石墨烯量子点中间,与2个六角石墨烯量子点中心的连线垂直.当间隙d比较大时,图3表明六角石墨烯量子点二聚物的等离激元激发时,2个六角石墨烯量子点保持电中性,相互之间的耦合是电容性的,π电子不能够在2个六角石墨烯量子点之间来回运动.比如,d=0.6 nm时,其光谱主要的低能吸收峰分别位于3.68和5.97 eV.图3中与其对应的电流I为零.当间隙d减小,2个六角石墨烯量子点中间的势垒降低时,电子可以隧穿过中间的势垒.2个六角石墨烯量子点之间的作用形式发生了改变.当间隙d=0.1 nm时,六角石墨烯量子点二聚物的低能等离激元共振模式对应的电流强度分布,和图1所示的吸收光谱相对应,即共振强度比较大的等离激元模式对应的电流强度也较大.虽然六角石墨烯量子点二聚物的低能等离激元共振能量变化不大,但是由于电子的隧穿,二聚物的等离激元共振模式发生了变化,已经不再是电容性相互作用.实际上,由于电子隧穿,电容性耦合的等离激元共振模式逐渐演变成另外一种新的等离激元共振模式.这种新的等离激元共振模式可以看作是长程电荷转移激发共振模式和电容性耦合等离激元共振模式的杂化耦合结果.

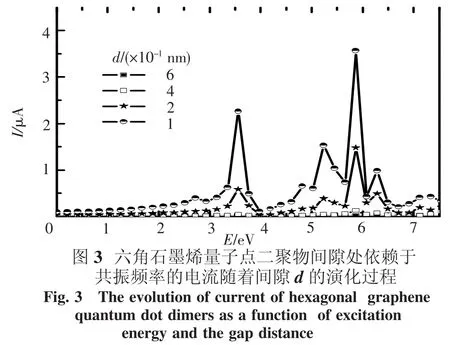
图4分别给出了单个石墨烯量子点(图4(a))和间隙为0.1 nm的六角石墨烯量子点二聚物(图4(b)),在能量为3.69和3.62 eV的等离激元傅立叶变换诱导电荷密度分布.傅立叶变换的诱导电荷密度计算公式为

通过变换,可以得到该频率集体激发所对应电荷的空间分布.图4给出的诱导电荷密度平面平行于石墨烯量子点所在的平面,两平面间的垂直距离为0.09 nm.对于单个六角石墨烯量子点,该等离激元共振模式的诱导电荷密度分布在量子点的边缘区域,具有类偶极子共振的特征.这主要是由于单个石墨烯量子点低能区的等离激元激发是一种长程电荷转移激发,沿激发方向,电子可以在很长一段距离内来回振动[10].图4(b)是在2个六角石墨烯量子点之间的间隙较小时,3.62 eV处低能等离激元共振模式对应的诱导电荷密度分布.该等离激元共振模式的诱导电荷密度分布,类似于2个单独排列的六角石墨烯量子点在3.69 eV处等离激元共振模式对应的诱导电荷密度分布.虽然量子点间的势垒降低了,图4(b)的结果再次表明,大部分π电子仍然主要在单个量子点中振动.由于间隙较小时,少部分电子可以隧穿过量子点间的势垒,在2个量子点之间运动,所以2个六角石墨烯量子点之间的耦合形式发生了变化,形成了一种新型的杂化等离激元共振模式.参与该杂化等离激元共振模式的大部分电子分别在2个石墨烯量子点中来回振动,少部分电子在2个石墨烯量子点之间来回振动.与金属纳米结构二聚物相比,石墨烯量子点间的耦合作用较弱.对于不同的间隙,在3.65 eV附近,六角石墨烯量子点二聚物中主要存在如图4(b)所示的这种等离激元共振模式.

2.2 矩形石墨烯量子点二聚物的等离激元激发图2给出了沿X轴方向,矩形石墨烯量子点和矩形石墨烯量子点二聚物的吸收光谱.从上向下,矩形石墨烯量子点二聚物的间隙分别为0.5、0.3和0.1 nm.插图为矩形石墨烯量子点和矩形石墨烯量子点二聚物的结构示意图.对于单个矩形石墨烯量子点,沿扶手椅方向激发时,体系中主要的低能共振吸收峰分别位于3.63和5.36 eV.对于矩形石墨烯量子点二聚物,当间隙d比较大时,2个量子点之间的相互作用是电容性的,没有电子可以穿过量子点之间的势垒.在间隙d=0.5 nm,沿扶手椅方向激发时,其光谱主要的低能吸收峰分别位于3.62和5.3 eV.同六角石墨烯量子点二聚物一样,当矩形石墨烯量子点靠近,通过电容性的相互作用时,二聚物低能共振区中主要的等离激元共振能量随着间距的减小发生了红移.随着间隙继续减小,量子点间的势垒降低,电子可以隧穿过势垒,在2个量子点之间运动.在低能共振区,矩形石墨烯量子点二聚物光谱吸收峰的强度进一步增加了,光谱的线形同样没有发生变化；并且,随着间隙的继续减小,低能共振区的吸收光谱也进一步发生了红移.由于电子隧穿,电容性耦合的等离激元共振模式逐渐演变成杂化等离激元共振模式.这种新的等离激元共振模式是长程电荷转移激发共振模式和电容性耦合等离激元共振模式的杂化耦合结果.与六角石墨烯量子点二聚物不同的是,随着间隙的减小,矩形石墨烯量子点二聚物在低能共振区2.92 eV附近出现了一些强度较弱的吸收峰.这种区别主要来源于石墨烯量子点形状不同引起的.

3 结论

用含时密度泛函理论系统地研究了,随着2个石墨烯量子点间的间距改变时,六角石墨烯量子点二聚物和矩形石墨烯量子点二聚物等离激元共振模式的演化规律.通过对计算结果的分析,得出以下主要结论.对于大的间隙,由于石墨烯量子点之间的势垒较大,π电子很难穿过势垒,二聚物中2个石墨烯量子点之间存在电容性的相互作用.在低能共振区,与金属纳米结构二聚物相同,石墨烯量子点二聚物的等离激元共振能量随着间隙的减小也发生了红移.当间隙进一步减小时,由于2个石墨烯量子点之间的势垒降低,电子可以隧穿过势垒在2个石墨烯量子点之间来回运动.对于小的间隙,吸收光谱、诱导电荷密度分布以及依赖于共振频率的电流分布表明,在石墨烯量子点二聚物中形成了杂化等离激元共振模式.该等离激元共振模式可以看作是长程电荷转移激发共振模式和电容性耦合等离激元共振模式的杂化耦合结果.与金属纳米结构二聚物中的长程电荷转移激发模式不同,石墨烯量子点二聚物中的杂化等离激元共振模式,随着间隙继续减小时并没有发生蓝移,而是继续红移.此外,随着间隙改变时,不同形状石墨烯量子点二聚物等离激元共振模式的演化规律基本相同,不依赖于石墨烯量子点的形状.石墨烯量子点等离激元共振模式之间的耦合较弱.

致谢感谢凯里学院规划课题基金(BS201301和Z1308)对本研究给予资助,谨致谢意.

[1]Novoselov K S,Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306(5696):666-669.

[2]曾晖,赵俊,韦建卫,等.含有碳链通道的石墨烯纳米带电子特性的第一性原理研究[J].四川师范大学学报:自然科学版,2013,36(1):87-91.

[3]Grigorenko A N,Polini M,Novoselov K S.Graphene plasmonics[J].Nature Photonics,2012,6(11):749-758.

[4]Vakil A,Engheta N.Transformation optics using graphene[J].Science,2011,332(6035):1291-1294.

[5]Cocchi C,Prezzi D,Ruini A,et al.Optical excitations and field enhancement in short graphene nanoribbons[J].J Phys Chem Lett,2012,3(7):924-929.

[6]Christensen J,Manjavacas A,Thongrattanasiri S,et al.Graphene plasmon waveguiding and hybridization in individual and paired nanoribbons[J].ACS Nano,2012,6(1):431-440.

[7]Ong Z Y,Fischetti M V.Theory of interfacial plasmon-phonon scattering in supported graphene[J].Phys Rev,2012,B86(16):165422.

[8]Ritter K A,Lyding J W.The influence of edge structure on the electronic properties of graphene quantum dots and nanoribbons[J].Nature Materials,2009,8(3):235-242.

[9]Kim S,Hwang S W,Kim M K.Anomalous behaviors of visible luminescence from graphene quantum dots:interplay between size and shape[J].ACS Nano,2012,6(9):8203-8208.

[10]Yin H F,Zhang H.Plasmons in graphene nanostructures[J].J Appl Phys,2012,111(10):103502.

[11]Li M,Wu W,Ren W,et al.Synthesis and upconversion luminescence of N-doped graphene quantum dots[J].Appl Phys Lett,2012,101(10):103107.

[12]Jin S H,Kim D H,Jun G H,et al.Tuning the photoluminescence of graphene quantum dots through the charge transfer effect of functional groups[J].ACS Nano,2013,7(2):1239-1245.

[13]Yan X,Cui X,Li B S,et al.Large,solution-processable graphene quantum dots as light absorbers for photovoltaics[J].Nano Lett,2010,10(5):1869-1873.

[14]Yan X,Cui X,Li L.Synthesis of large,stable colloidal graphene quantum dots with tunable size[J].J Am Chem Soc,2010,132(17):5944-5945.

[15]Li Y,Zhao Y,Cheng H,et al.Nitrogen-doped graphene quantum dots with oxygen-rich functional groups[J].J Am Chem Soc,2012,134(1):15-18.

[16]Zuloaga J,Prodan E,Nordlander P.Quantum description of the plasmon resonances of a nanoparticle dimer[J].Nano Lett,2009,9(2):887-891.

[17]Song P,Meng S,Nordlander P,et al.Quantum plasmonics:symmetry-dependent plasmon-molecule coupling and quantized photoconductances[J].Phys Rev,2012,B86(12):121410.

[18]Song P,Nordlander P,Gao S W.Quantum mechanical study of the coupling of plasmon excitations to atomic-scale electron transport[J].J Chem Phys,2011,134(7):074701.

[19]Tsai C Y,Lin J W,Wu C Y,et al.Plasmonic coupling in gold nanoring dimers:observation of coupled bonding mode[J].Nano Lett,2012,12(3):1648-1654.

[20]Marques M,Castro A,Bertsch G F,et al.Octopus:a first-principles tool for excited electron-ion dynamics[J].Comput Phys Commun,2003,151(1):60-78.

[21]李雪梅,李权,赵可清.外场作用下含羟乙基活性基团的噻唑生色分子的光谱和二阶非线性光学性质[J].四川师范大学学报:自然科学版,2010,33(2):231-234.

[22]刘芳玲,张红梅,廖显威.萘及其1-卤素取代化合物的荧光光谱的量子化学研究[J].四川师范大学学报:自然科学版,2009,32(4):490-492.

[23]Yabana K,Bertsch G F.Time-dependent local-density approximation in real time[J].Phys Rev,1996,B54(7):4484.

[24]Kim S,Hwang S W,Kim M K,et al.ACS Nano,2012,6(9):8203-8208.