可信性空间上变动生存年金的精算现值模型

杨 静

(北京航空航天大学，北京100191)

一、问题的提出

传统的寿险精算模型是建立在概率空间上，视人的寿命为随机变量，用概率测度进行度量［1-3］.然而，在现实世界，寿险中的不确定性往往表现为模糊性不确定性.如文献［4］指出，就寿命分布而言，由于人的生存和死亡的不确定性是十分复杂的，而概率是一种满足可加性(可列可加性)的测度，要描述一个人在某年龄的生存或死亡的可能性，概率的可加性条件是难以满足，因此用模糊测度——可信性测度代替概率测度，建立了可信性空间上的寿险精算模型.可信性测度是描述模糊性的新方法，文献［5］视寿险中的生命为可信性空间上的模糊变量，用具有自对偶、次可加性、正定性的可信性测度去度量，讨论了其中的一些基本问题，将寿险精算理论扩展到可信性空间上.本文在在可信性空间上，基于文献［5-6］讨论可信性空间上变动生存年金的精算现值模型，分别建立每年期初支付变动终身年金，期初支付变动n年年金，期末支付变动终身年金，期末支付变动n年年金.

二、预备知识

定义1［6］设Θ是一非空集合，P(Θ)为Θ的幂集，P(Θ)中每一个元素称为一个事件.若集函数Cr:P(Θ)→[0，1]满足:

(i)Cr{Θ}=1;

(ii)当 A⊂ B 时，Cr{A}≤Cr{B};

(iii)对于任意A∈P(Θ)，Cr{A}+Cr{Ac}=1;

(iv)对于任何Ai∈P(Θ)，若，有.则称Cr为一个可信性测度.

三元组(Θ，P(Θ)，Cr)称为可信性空间［7］.

定义2［7］设ξ为一从可信性空间 (Θ，P(Θ)，Cr)到实直线R上的函数，则称ξ为一模糊变量.

定义3［8］设ξ为模糊变量，函数Φ:R→ [0，1]满足

则称Φ为模糊变量ξ的可信性分布.

定义4［7］设ξ是定义在可信性空间(Θ，P(Θ)，Cr)上的模糊变量.那么，由可信性测度Cr可以导出其隶属度函数为

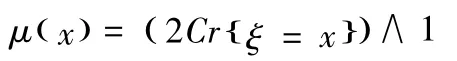
定理1［9］设ξ为模糊变量且可信性分布为Φ，假设Cr{ξ≤x}≠Cr{ξ≤x+t}(t＞0 )，则有

定义5 设T(x)为x岁的人的余寿，则称Φx(t)=Cr{T(x)≤t}(t＞0)为余寿分布函数

Φx(t)表示x岁的人在未来的t年内死亡的可信性，实际反映0岁的人活过x岁的条件下在x+t岁前死亡的可信性.

可信性空间中国际精算符号的定义［8］:

tqx表示x岁的人活不过x+t岁的可信性，即tqx=Φx(t)=Cr{T(x)≤t}

tpx表示x岁的人活过x+t岁的可信性，即tpx=1-tqx=Cr{T(x)＞t}=Sx(t)当t=1时，我们记1qx=qx，1px=px

t|uqx表示x岁的人在x+t岁与x+t+u岁之间死亡的可信性，即

当u=1时，我们记

定理2［7］ξ为可信性空间上的离散型模糊变量，若其隶属度函数为

不失一般性，不妨假设a1≤a2≤…≤an.则模糊变量ξ的期望值

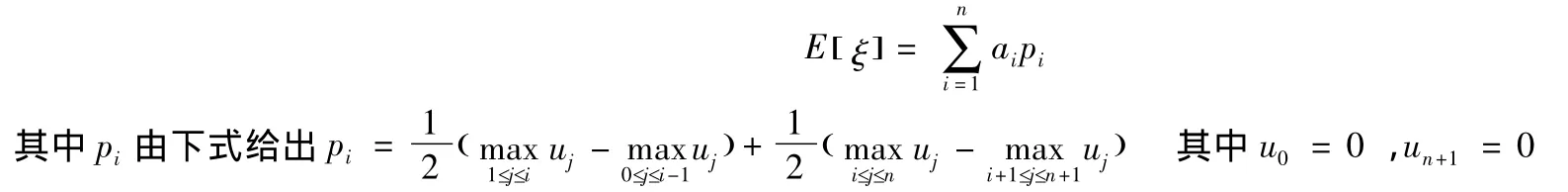
三、主要结果

(一)期初付变动终身生存年金的精算现值模型

一些符号规定如下:

K——x岁的被保人自保单生效后的取整余寿

Y——到被保险人死亡之时保险人所付的年金现值

v——折现因子

这里的K，Y均为可信性空间的离散型模糊变量

变动的生存年金:

在第一年支付1单位元的现值，第二年支付2单位元的现值，以此下去直至被保险人死亡.

需要说明的是人的寿命是有限的，我们假设被保人在整数极限年[W]岁上死亡，另对被保人来说，其第k+1年死亡的可信性为

x岁的被保人取整余寿K，则到死亡发生时为止的所有已支付的年金现值

这里的模糊事件{Y=yk+1}等介于事件{k(x)=k}

故有uk+1=[2cr{Y=yk+1}]∧1=[2cr{K(x)=k}]∧1=(2k|qx)

不失一般性，不妨假设y1≤y2≤…≤yk+1≤….于是由定理2的结论，得该年金的精算现值模型

(二)期初付变动n年生存年金的精算现值模型

(三)期末付变动终身生存年金的精算现值模型

(四)期末付变动n年生存年金的精算现值模型

四、结论

通过对可信性空间上年金的讨论，给出了可信性空间上生存年金精算现值模型，分别建立了年初，年末支付变动终身生存年金精算现值模型和年初，年末支付n年变动生存年金精算现值模型.从而使得可信性空间上寿险精算模型进一步得到完善.

［1］N.L.Bowers，H.U.Gerber，J.C.Hickman，D.A.Jones，C.J.Nesbitt，Actuarial Mathematics.The Society of Actuaries，Itasca，IL，1986.

［2］M.S.Dorfman，S.W.Adelman，Life Insurance.2nd ed.Dearbom Financial Publishing，Inc.1992.

［3］Y.Lei，Life Insurance Actuarial Science(in Chinese).Beijing:Beijing University Press，1998.

［4］H.J.Li，M.HmHa，Basic formations and model of life assurance on Quasi-probability space(in Chinese)，Journal of Hainan Normal University(Natural Science)，vol.21，no.4，pp.357–361，Dec.2008.

［5］M.Y.Yuan，Credibility distribution of a fuzzy variable that takes vale on interval.

［6］M.Y.Yuan，Basic formations of life function based on credibility measure.

［7］B.Liu，Y.K.Liu，Expected value of fuzzy variable and fuzzy expected value models，IEEE Transactions on Fuzzy Systems，vol.10，no.4，pp.445–450，2002.

［8］雷 宇.寿险精算学［M］.北京:北京大学出版社，1998.

［9］柏满迎，郑海涛.寿险精算学教程［M］.北京:人民邮电出版社，2007.