基于多因素模糊综合评价的最优旅游线路分析

徐永琳，王斐然

(1.西北民族大学数学与计算机科学学院，甘肃兰州730030;2.上海理工大学理学院，上海200090)

随着西部旅游事业的不断发展，兰州市自助旅游开始被越来越多的人选择.以兰州市10个景点的旅游路线选择问题为例，通过相关数据研究兰州市及其附近的10个景点的最短游览路线;对这10个景点的旅游价值作出较为合理的评估;结合评估结果，对追求旅游价值的游客给出合理的建议.

1 模型的建立与分析

从goolge上查到兰州市的电子地图如图1所示，从中确定10个景点作为研究对象，抽象出图2所示的网络图.

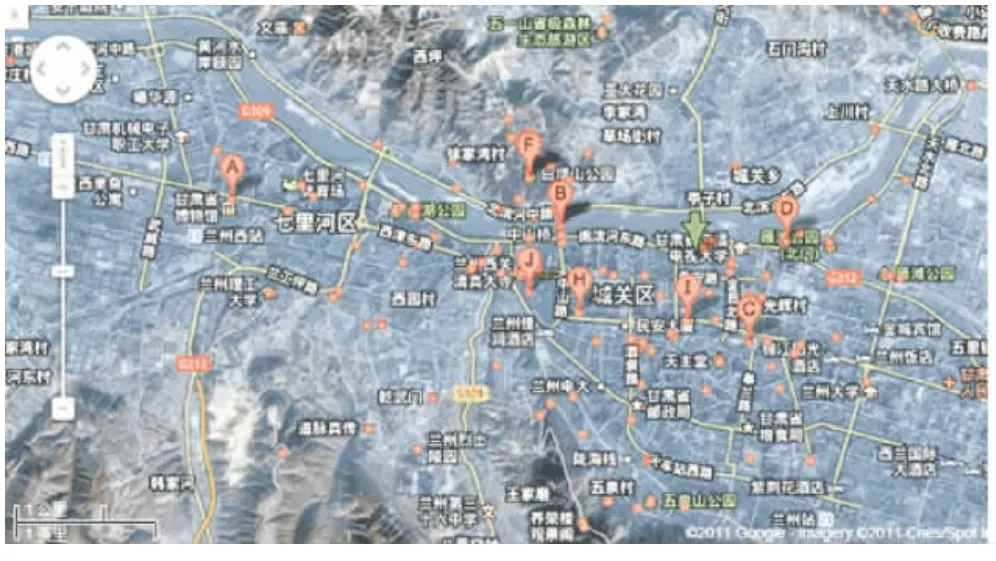
图1 兰州市电子地图Fig.1 Lanzhou electronic map

图2 兰州市网络图Fig.2 Lanzhou city network diagram

1.1 Kruskal算法求解

对于图2的网络图，根据Kruskal算法找出连通各点间的最短路径.由Kruskal算法［1－4］得出图3就是连通这10个景点的最短路径1.结合实际计算出D－E，E－F来回的路程为11.4 km，而J－F，F－E连线的路程为9.3 km，G－I来回的路程为4.6 km，而I－H之间的路程为4.1 km.得出如图4的最短路径2:即建议旅客从A点或从E点出发沿图4所示的路线的路程最短.

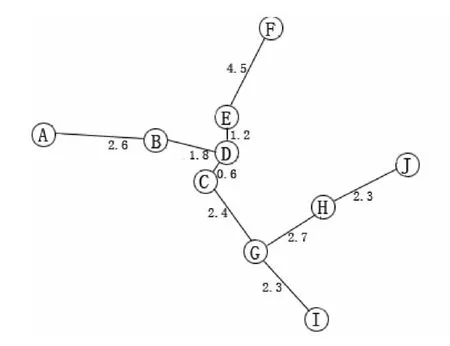
图3 景点最短路径1Fig.3 A shortest path 1

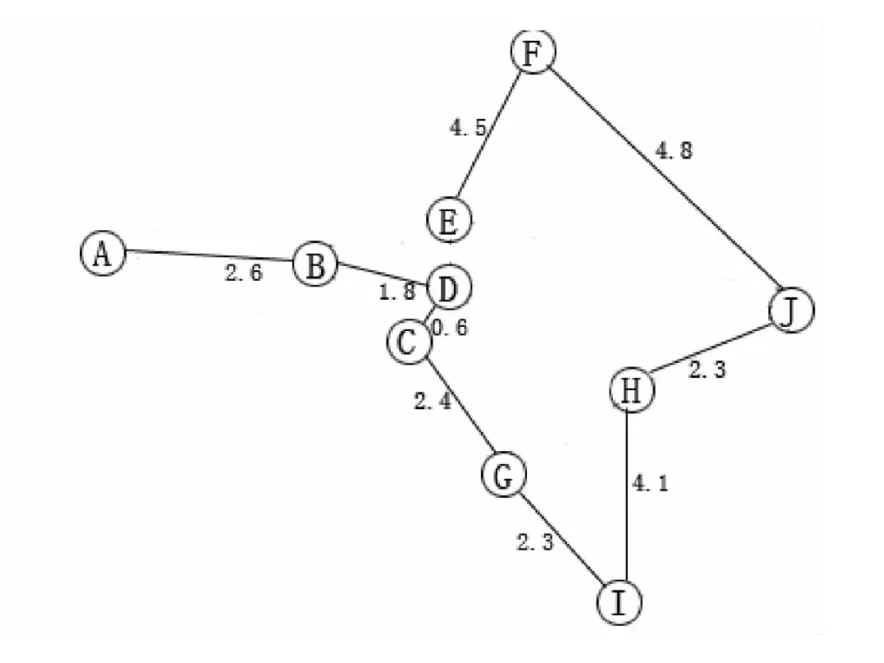
图4 景点最短路径2Fig.4 A shortest path 2

1.2 Dijkstra算法求解

对于图2所示的网络图，根据Dijkstra［5－7］算法求解，最终得出结果如图5所示.可以看出，根据Dijkstra和Kruskal算法所求解的结果一样，但这仅是理论上得出的最短连通路径，根据实际情况进行调整，计算出D－E，E －F来回的路程为11.4 km，而 J－F，F－E 连线的路程为9.3 km，G －I来回的路程为4.6 km，而 I－H之间的路程为4.1 km，得出如图6的最短路径4.

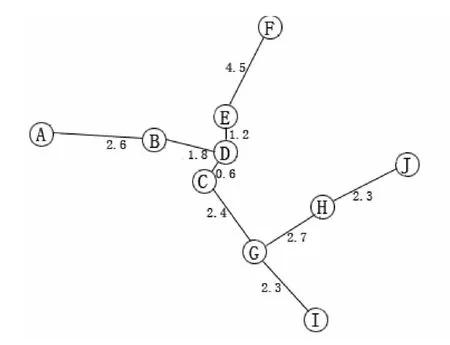
图5 景点最短路径3Fig.5 The shortest path 3

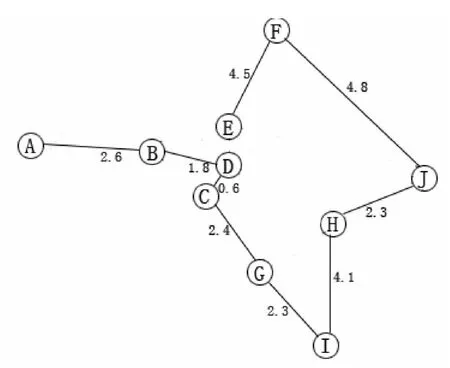
图6 景点最短路径4Fig.6 The shortest path 4

2 旅游价值模型的建立及求解

由于较难用价格来量化旅游价值，因此根据各个旅游景点的实际情况，综合考虑各景点的异同点，给出如下模型:取评价集为:V={很值得去，值得去，去过，没兴趣};因素集为:R～={服务态度，设施，好客度，门票};

由上述模糊集构成模糊矩阵为:

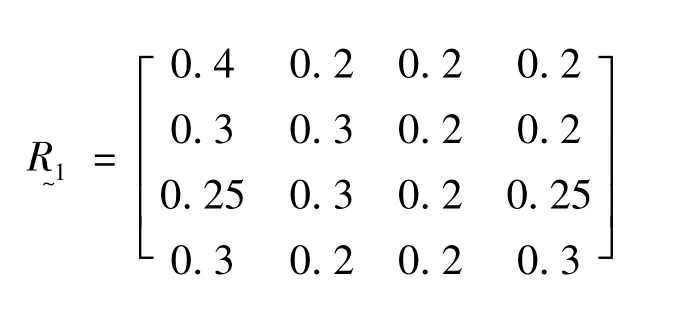
则对此景点的模糊综合评价为:

由于 0.4+0.3+0.2+0.2=1.1≠1，将综合评价结果归一化后变为:18，0.18).

这一评价结果表明37%的人觉得甘肃博物馆很值得去，27%的人觉得值得去，18%的人去过，18%的人感觉没兴趣.将这些评价集看成变量X，并且用(1～4)的具体值将其进行量化，最后求出变量X的期望值如下: E(X1)=0.37 ×4+0.27 ×3+0.18 ×2+0.18 ×1=2.83.

因此将此期望值作为该景点的旅游价值.

对兰州其它各旅游景点的旅游价值采用类似的方法，最终求得结果如下:

B:兰州西关清真寺

评价结果表明25%的人觉得兰州西关清真寺很值得去，30%的人觉得值得去，25%的人去过，20%的人感觉没兴趣. E(X2)=0.25 ×4+0.3 ×3+0.25 ×2+0.2 ×1=2.6.

C:兰州西湖公园

评价结果表明32%的人觉得兰州西湖公园很值得去，27%的人觉得值得去，27%的人去过，14%的人感觉没兴趣. E(X3)=0.32 ×4+0.27 ×3+0.27 ×2+0.14×1=2.77.

D:兰州黄河铁桥

评价结果表明33%的人觉得兰州黄河铁桥很值得去，25%的人觉得值得去，25%的人去过，17%的人感觉没兴趣. E(X4)=0.33 ×4+0.25 ×3+0.25 ×2+0.17×1=2.74.

E:兰州白塔山公园

评价结果表明33%的人觉得兰州白塔山公园很值得去，24%的人觉得值得去，24%的人去过，19%的人感觉没兴趣. E(X5)=0.33 ×4+0.24 ×3+0.24 ×2+0.19×1=2.71.

F:兰州五一山升级森林生态旅游区

评价结果表明27%的人觉得兰州白塔山公园很值得去，23%的人觉得值得去，27%的人去过，23%的人感觉没兴趣. E(X6)=0.27 ×4+0.23 ×3+0.27 ×2+0.23×1=2.54.

G:兰山公园

评价结果表明40%的人觉得兰州白塔山公园很值得去，20%的人觉得值得去，20%的人去过，20%的人感觉没兴趣. E(X7)=0.4 ×4+07.2 ×3+0.2 ×2+0.2 ×1=2.8.

H:兰州博物馆

评价结果表明29%的人觉得兰州白塔山公园很值得去，30%的人觉得值得去，19%的人去过，19%的人感觉没兴趣. E(X8)=0.29×4+0.3 ×3+0.19 ×2+0.19 ×1=2.63.

I:兰州五泉山公园

评价结果表明25%的人觉得兰州五泉山公园很值得去，25%的人觉得值得去，30%的人去过，20%的人感觉没兴趣. E(X9)=0.25 ×4+0.25 ×3+0.3 ×2+0.2 ×1=2.55.

J:兰州雁滩公园

评价结果表明30%的人觉得兰州雁滩公园很值得去，30%的人觉得值得去，20%的人去过，20%的人感觉没兴趣. E(X10)=0.3 ×4+0.3×3+0.2 ×2+0.2 ×1=2.7.

3 结论与建议

根据以上模型的求解得出下表1.

由于在一天之内，游客并不能将十个景点游遍，上述模型所求结果可以作为其路线选择的参考，对于具体的路线选择问题的解决，则采用0－1背包算法进行求解.为了便于算法的实现，将上述旅游价值表1中的数据进行放大100倍后得到表2.

为了便于研究，将各景点的旅游价值进行由大到小排序:

A:283、G:280、C:277、D:274、E:271、J:270、H:263、B:260、I:255、F:254.

对于于最求旅游价值最大化的游客而言，假设该游客的旅游起点为A，由于行驶路线多数处在市区中，因此综合考虑各种交通因素的影响，假设该游客乘坐的交通工具的时速为5 km/h，并且在每个景点停留一小时，一天的旅游时间最多为10小时.在一天所行驶的路程为25 km，则没有游遍十个景点.

采用0－1背包算法找出游客所能获取的最大旅游价值，因此，将25 km作为背包的容量C.则在此容量内，考虑如何能使游客所经过的景点的旅游价值总和最大，即在25 km的路程范围内所能囊括的景点的总价值最大.

方案1:

先选旅游价值最大的景点放入背包中，根据上述各景点的旅游价值大小顺序，则其旅游路线为:

A→G→C→D→E→J→H→B→I→F

按此路线旅游，则在旅游总路程S≤25的约束条件下，该游客只能到达B景点，因为A→G→C→D→E→J→H→B→I的总路程为28.5km﹥C，因此A→G→C→D→E→J→H→B的总路程为21.6km，则其获得总的旅游价值为:1908.

方案2:

按照Kruskal算法得出的最短旅游路径作为旅游的路线为:

A→B→D→C→G→I→H→J→F→E，由于总路程为25.4 km＞C，则该游客所能经过的景点为:A→B→D→C→G→I→H→J→F，其总路程为20.9 km，所能获的总的旅游价值为2146.因此，通过比较分析，无论对于追求旅游路线最短还是追求旅游价值最大，方案二比方案一更优.因为方案二不仅旅游路程较短，而且所获得旅游价值较大.

表1 各景点的旅游价值Tab.1 The scenic spots in the tourism value

表2 各景点的旅游价值Tab.2 The scenic spots in the tourism value

［1］ 刁在筠，刘桂真，宿洁，等.运筹学［M］.北京:高等教育出版社，2007:201－203.

［2］ 李士勇.工程模糊数学及应用［M］.哈尔滨:哈尔滨工业大学出版社，2004:96－101.

［3］ 王晓东.算法设计与分析［M］.北京:北京教育出版社，2008:92－94.

［4］ 赵静，但琦.数学建模与数学实验［M］.北京:高等教育出版社，2009:181－187.

［5］ 李涛.Matlab工具箱应用指南——应用数学篇［M］.北京:电子工业出版社，2000.

［6］ 姜启源，谢金星，叶俊.数学模型［M］.北京:高等教育出版社，2003.

［7］ 林浩，皮军德.有向网络上单源多汇的最优连接问题［J］.系统工程学报，2008，23(1):162－168.