Trie树路由查找算法在网络处理器中的实现
张 琦,金胤丞,李 苗,章建雄
(中国电子科技集团公司第三十二研究所,上海 200233)
1 概述
国际互联网络规模的高速增长对 IP(Internet Protocol)路由查找算法处理大容量路由表的适应性提出了更高要求,骨干路由器每秒所需转发的报文数随之剧增,IP路由查找算法的优劣直接影响了当前和未来互联网的整体性能[1]。此外,随着网络系统的发展,现有网络系统的瓶颈越来越明显,为了解决这些问题,研究者提出了网络处理器(Network Processor, NP)解决方案。网络处理器是面向网络应用领域的专用指令处理器,是面向数据分组处理的、具有特定电路的软件可编程器件。它将RISC(Reduced Instruction Set Computer)处理器的低成本、灵活性与ASIC (Application Specific Integrated Circuit)专用网络处理芯片的高性能、可扩展性很好地结合在一起[2]。网络处理器中查找微引擎的设计是处理速度提升的关键,所以,查找微引擎中路由查找算法的研究对实现高速网络处理器具有直接和重要的意义。
另外,在此网络环境下查找算法应满足下列条件:(1)存储器访问最坏情况下应不大于一个合理的、确定的次数,平均访问次数应满足转发速率的要求。(2)确定合理的最坏情况路由表更新操作,不影响正常转发速率所要求的路由表查找操作。(3)具有较高的存储空间利用率。对于一定的路由表表项深度,所占的存储空间应尽可能小,且路由表的大小对算法的查找性能影响不大。(4)实现所需的物理器件应有较低的成本,适合应用于实际的产品。(5)数据结构与查找操作相对简单,适合于硬件实现[4]。
本文提出一种 IP路由查找算法应用于交换速率为10 Gb/s的网络处理器中,按照每个数据包长度为80 Byte计算,如果要实现线速转发,则至少需要达到10 Gb/s/((80+12)×8)=13.58 Mb/s的路由查找速率[3]。
2 路由查找算法分析
实现地址最长前缀匹配是路由查找算法的难点,在前缀匹配的过程中要考虑地址前缀的长度以及地址前缀的值,现有的路由查找算法都可以归结为这 2个方面的匹配查找过程。具体的,基于地址前缀长度的路由查找算法考虑的是在长度空间内进行查找,可以在查找过程中使用线性遍历法或者二分遍历法;基于地址前缀值的路由查找算法为消除地址前缀长度对查找的影响,采取穷举整个地址前缀空间地址关键字的方法。
常用的路由查找算法主要有基于线性表查找结构的线性查找算法、基于Hash表结构的路由查找算法、基于Trie结构的路由查找算法[5]。
基于 Trie树的算法[6]因为具有较好的查找速度、时间复杂度和空间复杂度,并且还能适应不断提高的路由器性能要求,所以现代快速的路由查找算法都是基于Trie树算法优化实现的,如路径压缩Trie树算法、多分支Trie树算法以及基于Trie树的前缀扩展等策略的算法。假设地址关键字长度为 W,地址前缀表中前缀数目为 N,则有如表 1所示的典型算法复杂度分析列表。
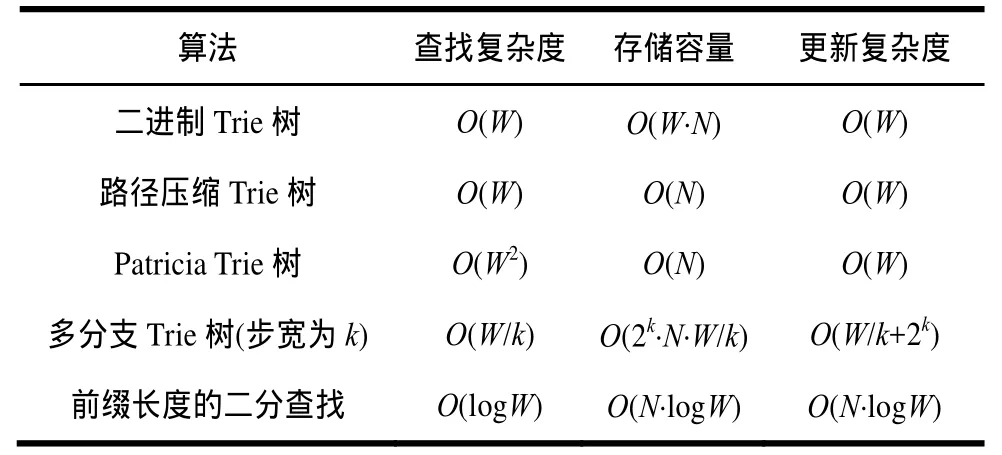
表1 典型算法的复杂度分析
对于基于Trie树的算法,树高决定了访存次数,从而决定了算法的时间性能。对于路径压缩Trie树算法,与二进制树算法一样,查找过程中需要大量的存储器访问操作。对IPv4来说,一颗完整Trie树的深度是32,最坏情况下需要32次存储器访问。而多分支Trie树算法采用大于1的查找步宽,从根本上降低了树的高度,查找性能得到很大程度的提高。
事实上,IP路由查找算法很难同时满足查找速度、更新速度、空间利用率等 3个方面的要求。传统上仅采用一种算法或者方法会导致查找性能受到一定的限制,即便可以实现很快的查找速度,往往也有转发表更新困难或者扩展性差等问题[7]。
本文提出基于查找速度快且易于硬件实现的Trie树的路由查找算法,吸取压缩Trie树和多分支Trie树的优点,通过一些软件建树和硬件查找策略,以在上述 3个方面取得平衡优势。
3 路由算法实现
3.1 IP地址前缀的树型结构表示
本文提出一种基于最优平衡、多层存储的Trie树算法,即建立一种平衡的压缩树结构;然后将该树中相邻的多层节点压缩到一个存储节点中。其中借鉴了Patricia Trie树数据结构思想[8],即通过路径压缩算法删除路径上的一些单去向节点,经过选列(即被选测试位)压缩了冗余节点,而树搜索时仅对被选位进行测试比较,大大减少了测试比较次数,以及内存占用空间和访存次数。一个Patricia Trie树结构如图1所示。
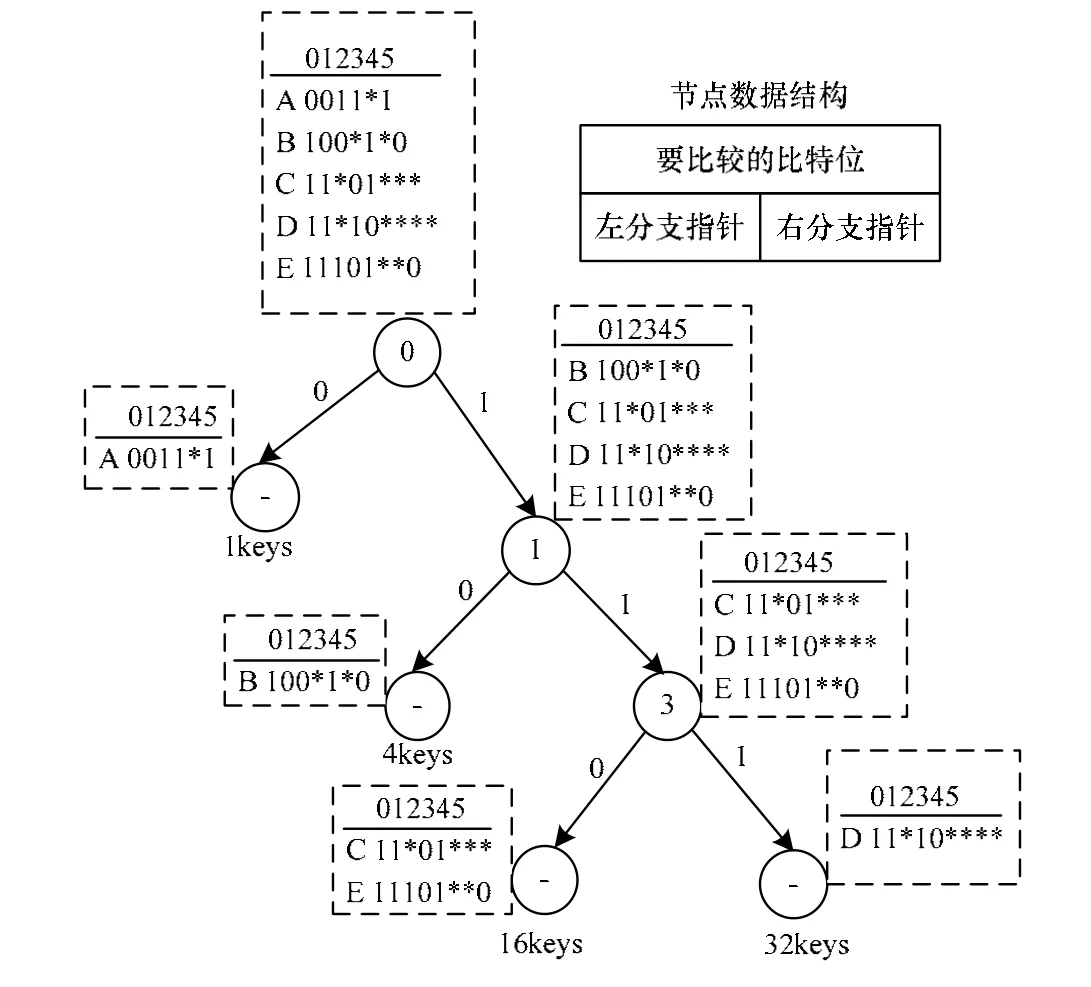
图1 Trie树结构举例
建树过程的具体实现步骤如下:
(1)每次建立一颗子树后,开始消除不考虑的条目。即从所有条目中剔除不能够和其他条目区分的条目,压缩冗余信息。
(2)选列。即查找条目中的一个或多个有不同的指定值的列。首先,被选列必须是既有“0”又有“1”的列(才有分支的可能)。其次,列中“0”和“1”的数目应较多且相近,以把较多的规则分开到 2个不同的组中,“0”表示走向左子树或叶子;“1”表示走向右子树或叶子;“*”表示范围域的范围之内,或是掩码值域的掩码未作屏蔽,故走向左、右子树或叶子均可。
(3)若步骤(2)查找条件匹配,应先选择含有通配符“*”数目最少的列。若这样的列仅有一个,直接进入步骤(5)。若满足条件的列有多个,则采用子树内部关键字的最优平衡准则建树。
图2是采用平衡准则建立的一颗子树,与图1中普通的Patricia Trie子树相比较,平衡准则优先把含通配符数目较多的关键字置于深度较小的子树中,以达到降低关键字平均搜索深度的目的。

图2 最优平衡子树建立
(4)若步骤(2)查找条件不匹配,算法检查当前条目集合是否能插入一个叶子。若可以,则建立叶子并定义为叶子节点,子树建立完成。否则,如当条目集合超过1000个时,超过了硬件限制的叶子数量则无法插入新的叶子。
(5)选择条目的值为 0建立左子树,选择条目的值为 1建立右子树,然后采用递归的方式回到步骤(1)。每当建立新子树,将新子树链接为当前节点的孩子,并且定义为内部节点,内部节点不含关键字路由信息。所提出的树的结构和算法中建树部分解决了 2个问题:含有通配符条目的编入与不同长度条目的编入。
当树建立之后,将其按照如图3所示的结构进行存储,在图3(a)中,树结构被分成若干子树进行存储,每一棵子树放在一个存储单元中,只需要进行一次访存操作,一棵子树包含多个存储节点,能实现多位关键字查找;故而在进行数据查找的过程中,一次访存可以进行多次数据查找,如图 3(b)所示,在该子树结构所代表的结构中,一个存储单元为256位,代表了树结构中3层,即可以对关键字进行3次查找,缩短访存时间。
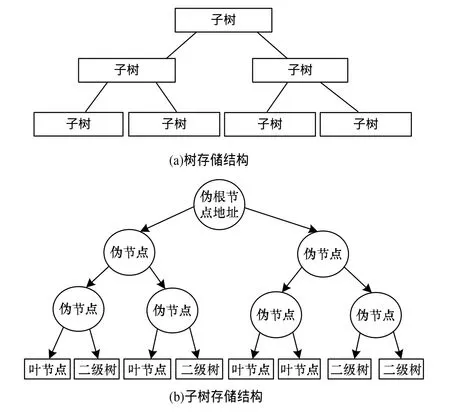
图3 树形结构
3.2 硬件路由查找过程
子树信息位于存储器中,首先提取一个子树的地址,然后根据地址从内部存储器中取出相应的数据。根据解析表相应位,确定该树型结构的拓扑图。解析拓扑结构图,判断是否为该子树的叶节点。若是继续下一步,否则继续解析。接着判断是否为整棵树的叶节点。若是,从外部存储器中读出相应的数据。若否,递归方式重新提取子树地址。最后将读出值的叶子节点值比较。若一致,返回查找结果,若不一致,返回默认值。
基于Trie的硬件路由查找过程状态机如图4所示。

图4 树查找状态机
硬件路由的查找过程如下:
(1)MEM_ACCESS
首先确定根节点的值,根节点地址都存储在片内寄存器中。提取一个子树的地址,然后根据地址从内部存储器中取出相应的 256位数据。每一棵子树的存储信息为256位,其代表的含义如图5所示。
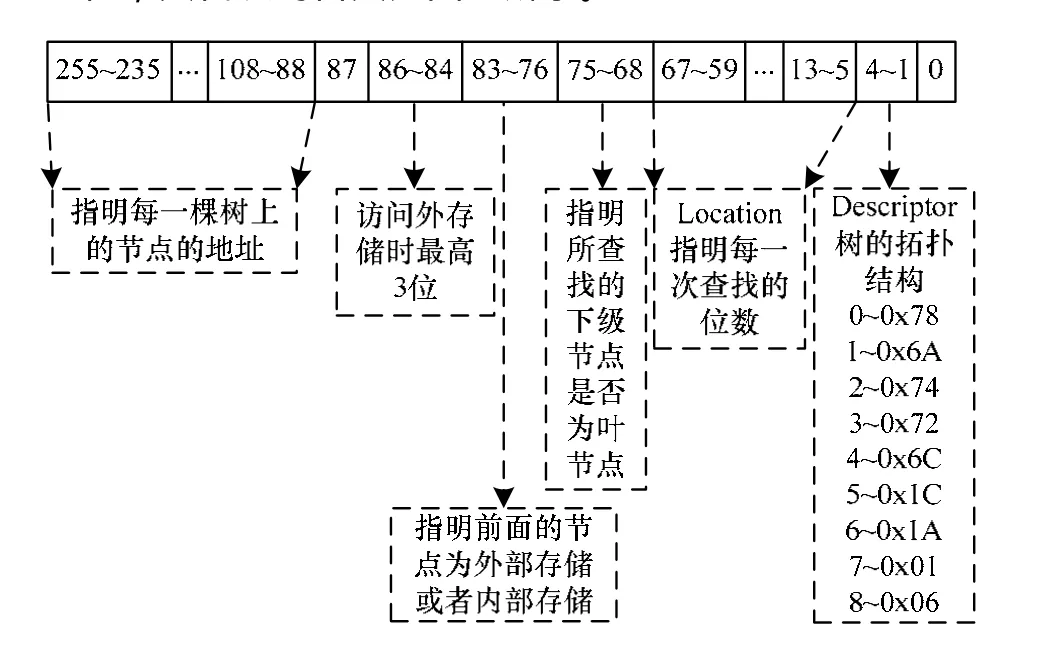
图5 节点数据字段解析
(2)SUB_LEAF
读出该节点的值后,根据图中拓扑结构描述符Descriptor[4:1],判断每一棵子树所对应的拓扑图,解析出该4位所对应的值value[7:0],根据value的值从低位到高位,确定拓扑结构,value[i]的值表明该节点是否为该子树的叶子节点,1表示是;0表示否;非叶子节点可以挂接另外2个伪节点;在叶子节点上,挂接2个另外的二级子树的根地址或者整棵树的叶子。例如:Descriptor[4:1]为0001时,value[7:0]为 01101010,那么该的树的拓扑结构如图 6所示,同理,还存在其他8种树的拓扑结构。

图6 子树拓扑结构
根据解析的拓扑结构图,判断是否为该子树的叶节点。若是,继续下一步,否则继续解析直到叶节点为止。
(3)TREE_LEAF
判断是否为整棵树的叶节点。对读出值进行判断是否为整棵树的叶子节点时,即根据图 2中[75:68]位,判断二级子树中对应的结构为整棵树叶子节点或者二级子树,1表明为叶子,0表明为二级子树。若是,当为整棵树的叶子节点时,利用图 2中[83:76]位确定从内部或者外部存储器中读出数据,读出该地址所对应的值。若否,递归回到步骤(1)。
(4)COMPARE
将读出值与上一级输入的 key(包含 IP地址的关键字)的相应值比较。
(5)OUT
如果相等,则证明查找到结果,返回查找结果result(包含路由等信息的结果);如果不相等,则证明查找出错,返回默认的值。当为二级子树时,返回到步骤(1)继续开始做,直至找到叶子节点的值为止。
3.3 算法硬件的实现
该网络处理器有解析、查找、解决、修改 4种类型的微引擎,每个都被优化执行一个特殊的任务,实现对数据包的分类、转发和修改,本文算法在查找微引擎中实现。微引擎采用一种独特的体系结构,带一个定制的、特殊功能的数据通路和指令集。这减少了复杂数据包操作需要的时钟周期数目,提供相当快速的数据包处理。微引擎性能受益于超标量结构,多个实例在每个流水段并行运行。查找微引擎接收解析微引擎输入的查找关键字key,以及各种查找结构的匹配,执行对表的查找。查找结构存储在若干内部和外部存储器中。查找微引擎将最终的查找结果result传递到下一级微引擎处理。
如图 7所示,算法硬件采用 65 nm工艺实现,包含三大模块:处理器模块,I/O模块,存储器模块。处理器模块包含 4个并行处理查找微引擎;存储器模块包含指令存储器和数据存储器,数据存储器分为内部存储器和外部存储器,分别采用SRAM和DRAM实现,微引擎从数据存储器中的树型结构中获取所需要的信息。

图7 算法实现的硬件结构
4 仿真与性能分析
4.1 算法仿真验证
查找算法采用 Verilog HDL语言编写,开发环境为Xilinx公司ISE14.1软件,仿真工具为QuestaSim 6.6a。通过随机输入key=0h09004200进行测试,即作为输入的目的IP地址(在存储器中key的存储是按低字节在左)。如图8方框所示,该key(0h00420009)在路由表中对应的路由查找信息 result为 0h0300000009000009000000410009FC00。图 9为路由查找的时序仿真图,key_reg和result_reg分别为查找key和查找最终返回值。图8和图9的结果验证了查找电路时序正确,实现了所设计的路由查找功能[9]。
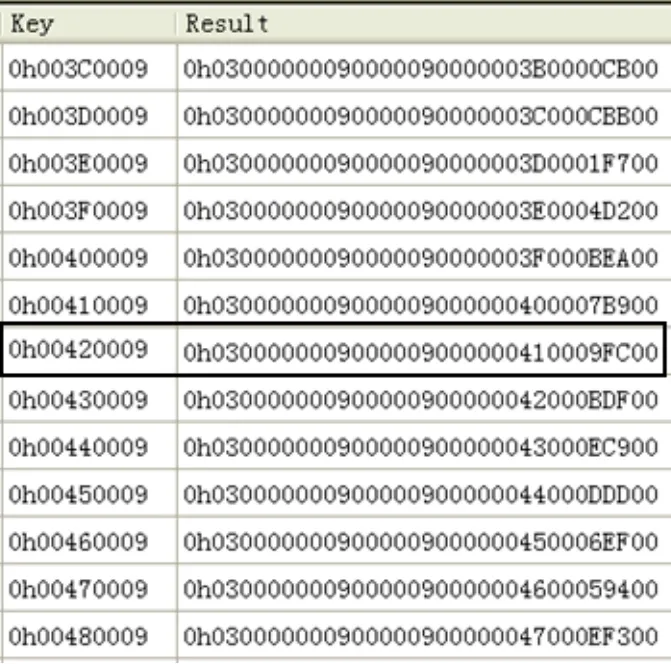
图8 存储器中的路由表信息

图9 仿真验证结果
4.2 算法性能分析
影响路由查找算法性能的主要因素是查找时间复杂度、存储器复杂度和更新时间复杂度[10]。对于查找时间复杂度,首先实现了创新压缩算法,减少查找的地址前缀长度。其次提议算法比其他压缩二进制树更进一步,本文一次访存可以进行 3次数据查找,减少典型查找的次数到正常需要查找操作的 1/3,即存储器访问次数为原来 1/3。对于子树的查找,查找步长可变,其查找时间复杂度为O(子树的深度)≈O(logN),存储空间复杂度为 O(1)。对于整棵树,若查找步长为 k,时间复杂度为 O(W/k),节点数为O(N),故存储器复杂度为O(N)。地址前缀更新操作首先要进行一次查找过程确定更新节点的位置,因此更新时间复杂度和查找过程相同,为O(W/k)。
为对算法性能有一个更加直观的认识,对几种常用快速软件路由算法进行了仿真比较[11],测试数据使用 http://www.meri.edu/ipma/routing_table提供的 MAE-EAST路由表,其中包含路由表项 38项和 816项,该测试系统使用2.8 GHz(Pentium4)处理器,求出查找不同前缀长度路由信息所消耗时间的统计平均值,经过换算后的比较结果如表2所示。本文设计算法在最坏情况下查找一次需要访问10次SRAM和1次DRAM,如果使用500 MHz的SRAM和800 MHz的 DRAM,访问一次存储器分别需 5个周期和100个周期,那么需要的时间是225 ns,存储容量为220 KB。
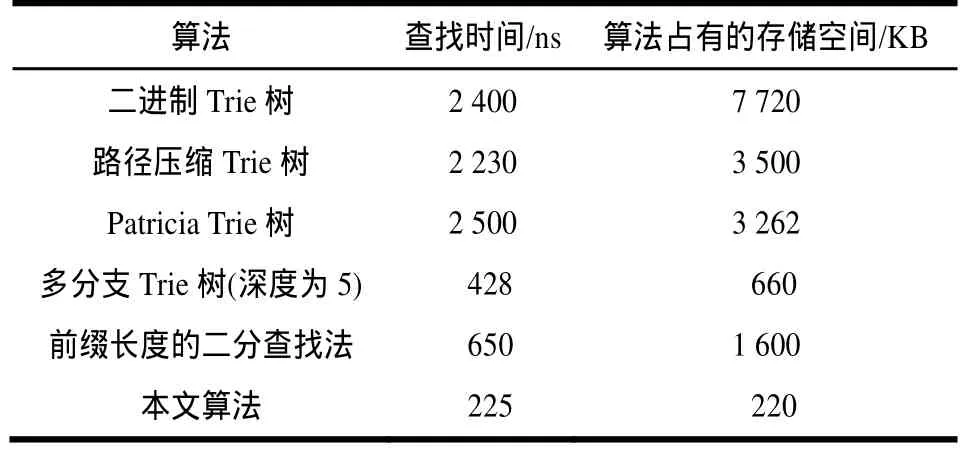
表2 算法实际运行性能比较
从表2的对比中可以看出,提议Trie树算法比传统快速Trie算法在路由查找速度方面有较大的提升,在IPv4的环境下,提议算法比二分查找算法速度也有明显提升;算法存储空间比这些传统的快速路由算法较为节省。使用提议算法一次查找过程只需 225 ns,因此,查找速度可达到4.4 Mb/s,应用于4个并行处理的微引擎中,可使网络处理器达到万兆的交换速率。
5 结束语
高效的IP路由查找算法应该综合考虑查找速度、路由表更新的开销,以及所需存储空间的大小等方面,以取得较佳的综合性能为主要目标[12]。本文提出一种基于Trie树的路由查找算法,通过硬件查找机制具有查找速度快、所需存储空间小、更新速度快、硬件实现简单等特点,已成功应用于 10 Gb/s带宽的网络处理器设计中。由于下一代Internet协议采用IPv6协议,路由地址扩展为128位,因此在网络处理器的实际应用中,该算法对IPv6的支持是下一步要展开的工作。
[1]Chang Y K , Lin Y C.A Fast and Memory Efficient Dynamic IP Lookups Algorithm Based on B-tree[C]//Proc.of International Conference on Advanced Information Networking and Applications.Bradford, UK: IEEE Press, 2009:278-284.
[2]李 韬, 孙志刚.基于SoPC的粗粒度数据流网络处理器原型设计[C]//第五届中国通信集成电路技术与应用研讨会论文集.西安: 中国通信学会, 2007.
[3]刘英臣, 傅光轩.路由查找技术的分析及研究[J].贵州大学学报: 自然科学版, 2006, 23(3): 294-299.
[4]刘永锋, 杨宗凯.高速路由器中基于树型结构路由查找算法的研究与实现[J].计算机工程与科学, 2004, 26(1): 22-25.
[5]华 泽, 马 涛.基于Trie的路由查找设计与实现[J].计算机与现代化, 2006, 22(2): 42-45.
[6]科 默.网络处理器与网络系统设计(英文版)[M].北京:电子工业出版社, 2004.
[7]郜国良, 李广军.一种基于Trie的快速IP路由查找算法[J].微电子学与计算机, 2011, 28(6): 163-167.
[8]吴 强, 苏金树, 王勇军.基于 Patricia树的快速多维分组分类算法[J].计算机工程, 2004, 30(21): 50-52.
[9]田 园, 张曙光, 乔庐峰, 等.路径压缩查找算法的 FPGA实现[J].军事通信技术, 2012, 33(3): 48-52.
[10]郭文文.基于 Trie的软转发路由查找模块的设计实现[D].南京: 南京邮电大学, 2011.
[11]张 毅, 郭玲丽.基于FPGA的高速路由查找算法[J].电子元器件应用, 2009, 11(9): 22-27.
[12]谭明锋, 高 蕾, 龚正虎.IP路由查找算法研究概述[J].计算机工程与科学, 2006, 28(6): 77-80.

