两车间可调度工序均衡处理的综合调度算法
谢志强,郑付萍,朱天浩,周含笑
(哈尔滨理工大学计算机科学与技术学院,哈尔滨 150080)
1 概述
产品制造调度问题是NP难问题[1],目标是在满足约束条件的前提下,使产品的加工时间尽可能少。以往对大批量相同产品采用流水线方式生产制造的调度方法主要是纯加工调度[2-3]和纯装配调度[4-5],但随着社会对产品多样化的需求,多产品小批量的生产计划越来越多。对多品种小批量产品,特别是单件复杂产品,如果按以往先加工后装配的方式制造,必然要割裂产品内在的加工与装配的并行关系,文献[6]提出产品制造的第3种调度方式:加工和装配一同处理的综合调度。随着综合调度研究的深入,目前有关综合调度的研究已解决了一般综合调度问题[7]、工序间存在特殊约束关系[8]、柔性产品[9]、存在相同设备[10]和存在批处理设备[11]等的综合调度问题,但所解决的综合调度问题仅限于设备资源在单车间的情况,目前还无人考虑单件复杂产品在相同设备资源两车间制造的分布式综合调度的实际问题。
对于单件复杂产品在两车间分布式制造的调度问题,主要的研究目标是设计使产品尽早完成的调度方案。为了使产品尽早完成,需要解决以下问题:(1)两车间充分并行处理,即让两车间工序加工的时间差尽量小;(2)工序在两车间移动的次数尽量少。
对于问题(1),考虑到叶节点工序为可同时加工工序[12],即叶节点工序可充分并行处理,本文首先将原始叶节点工序成批调度处理,再将每次动态生成的叶节点工序分批处理,即可调度工序分批处理。考虑到两车间充分并行处理,即减少在两车间形成的工序加工时间差,将每批工序按加工时间尽量均衡地分为 2组。借鉴单车间综合调度中的设备均衡策略[13],在相同设备的两车间上,提出使得分配工序时间之和尽量相等的可调度工序车间均衡策略。对于问题(2),采取将已分组的工序分配到其紧前工序个数较多车间的方法,以降低工序的位移次数,为此提出分组工序车间确定策略。
2 问题描述
对于树状结构的单件复杂产品,叶节点工序为初始时可加工的工序,根节点工序为最后加工的工序。由于产品加工过程中形成的紧前工序集为空的动态叶节点工序为可调度工序,于是设动态叶节点工序集为可调度工序集。为了减少产品完成时间,计划将每批可调度工序进行适当合理的分组并分配到两车间,为此定义可调度工序分组的相关概念:工序设备分组,车间均衡和设备均衡组。
定义 1(工序设备分组) 对于动态形成的一批可调度工序,按设备种类进行分组称为工序设备分组。
定义 2(车间均衡) 将按设备形成的分组再按车间均衡分配,使分配到两车间的工序占用设备的时长差△T相对较小。
定义 3(设备均衡组) 通过车间均衡处理产生的车间分组称为设备均衡组。
根据定义 2与可调度工序集的特征,通过对可调度工序集均衡处理可使产品在两车间分布式加工充分并行,达到减少产品加工时间的目的,于是提出了两车间可调度工序分组均衡处理的综合调度算法,并建立相关的数学模型。
由于综合调度是将产品加工工序和装配工序统一为加工工序,加工设备和装配设备统一为设备一同处理的调度方式,于是一个有n道工序的产品在m台设备上进行分批综合调度的约束条件如下:
(1)一台设备在某一时刻只能加工一道工序,且一旦加工某道工序,必须满足该工序加工完毕后,这台设备才可以加工其他工序。
(2)某道工序在某一时刻只可以占用两车间中相同设备中的一台设备进行加工。
(3)可调度工序集加工完毕才可以开始下批可调度工序加工。
(4)允许工序之间等待,允许设备在工序到达之前闲置。
由于本文讨论的综合调度算法是在满足上述约束条件下,按动态形成的可调度工序集分批调度,每批可调度工序加工开始的时间为上一批可调度工序加工完毕的时间,每批可调度工序加工完毕的时间为按工序设备分组后在两车间中设备完工的最大时间值,于是本问题的数学描述为:
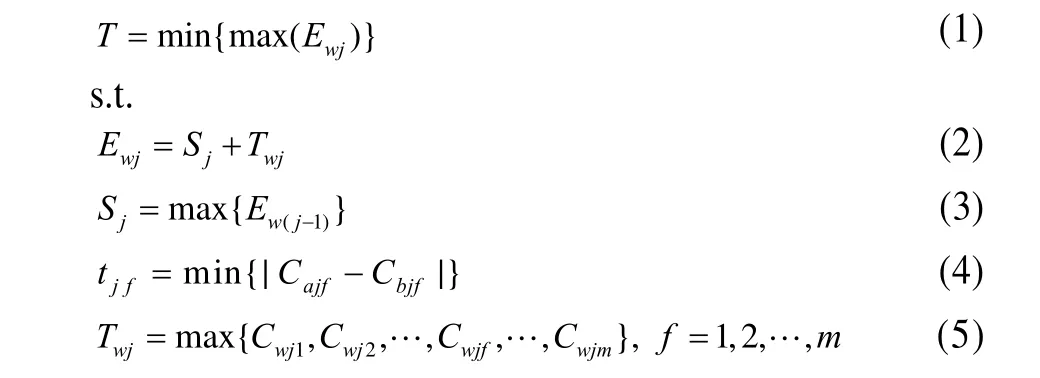
其中,w代表a、b两车间,可调度工序批次为j=1,2,…,k;Ewj是每批的完成时间;Ewk为产品完成时间;Sj为每批可调度工序的开始加工时间,即上批可调度工序的完成时间,第1批可调度工序的开始加工时间为S1=0;Cwjf为第j批可调度工序在 w车间的设备 f上组合工序的加工时间和;tjf是设备均衡组工序加工时间差;式(5)表示第 j批可调度工序在w车间各设备完工的最大值。
3 分配方案设计与分析
为减少产品两车间分布式综合制造的时间,可从 2个方面考虑:(1)使产品在两车间充分并行制造;(2)减少两车间工序移动占用的时间。于是研究使产品工序在两车间加工时间差相对小和工序在两车间移动次数少的调度方案。
由于每批可调度工序可并行处理,为了减少两车间加工时间差和工序移动次数,设计了可调度工序车间均衡策略和分组工序车间确定策略。
为方便按批调度工序,本文设置工序的属性:qi|Mwi|ti|Fi|ei|Li,其中,qi为工序名;Mwi为工序 qi所在车间 w(a或b)的加工设备;ti为工序qi的加工时间;Fi为工序qi的紧前工序集;ei为集合 Fi中工序的个数;Li为工序 qi的紧后工序,i∈{1,2,…,n}。一般情况下,工序属性只需前3项就可以实现产品加工的策略和方案,本文添加了紧前工序集、紧前工序个数和紧后工序,可根据紧前工序个数为空动态生成可调度工序。
3.1 可调度工序车间均衡策略
一般产品充分并行制造要求设备均衡加工,根据文献[13],设备均衡是指工序的加工设备不唯一时,选择已加工时间和最小的设备作为该工序的加工设备。对于相同设备两车间的产品制造,当要求两车间所有相同设备对每批可调度工序都均衡加工时为车间均衡,因此,车间均衡是基于设备均衡提出的。由定义2,车间均衡与设备均衡区别如下:
(1)相同点:2个均衡都是针对设备的。
(2)不同点:设备均衡是针对一种设备且考虑以往工序加工情况,车间均衡是针对两车间中所有的相同设备且只考虑同批可调度工序。
对每批可调度工序进行分配时,根据定义 1对设备进行分组,针对每个工序设备分组采用本文设计的车间均衡策略达到车间均衡。下面详细说明车间均衡策略:
(1)当某工序设备分组中工序唯一,此时该设备无需考虑均衡;
(2)当某工序设备分组中仅有 2个可调度工序,将这2个工序分别分配到两车间;
(3)当某工序设备分组中可调度工序数大于等于3时,有以下2种方案。
方案1 工序动态调整。
因为两车间工序设备分组中设备m上工序均衡分组的重要指标是该工序设备分组中所有工序的加工时间和除以车间数2的值Pm,即在本文中为该工序设备分组中所有工序的加工时间和的一半,所以该均衡方案的目标是让设备均衡组的2个组合工序加工时间值与Pm的差值尽量小。具体实现步骤如下:
步骤1 分组时考虑有序序列比无序序列针对工序调整的确定性强、对后续的工序调整的操作便捷以及时间复杂度小,于是先将工序设备分组中的工序按加工时间ti升序排序得序列H。
步骤2 按序将H中的值累加到D中,直到首次满足均衡差△T=D–Pm≥0,记录累加的工序序列为 G,将其他工序存放到升序序列B中。
步骤3 对均衡差△T进行处理。若△T=0或△T值小于H中的第1个工序的加工时间,已达到最优均衡,记录设备均衡组;否则将△T与 G中的其他项进行比较,若△T等于G中某项,则将此项调整到序列B;若△T介于G中某相邻两项值之间,则将G中与△T接近的工序调整到B中。
方案1可调度工序车间均衡策略实现流程如图1所示。
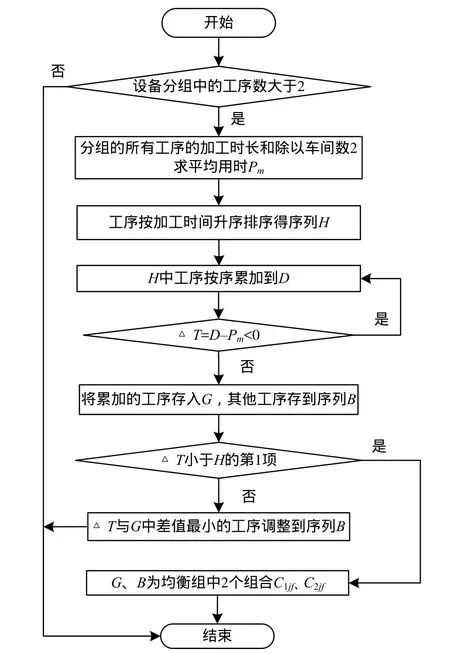
图1 可调度工序车间均衡策略实现流程
方案2 根据幂集值确定。
具体方法是:首先确定设备m的最优均衡时间Pm;然后求该工序设备分组的幂集;其次计算每个幂集中的工序按属性ti累加和D并计算均衡差△T=D–Pm,记录△T最小的值;最后将△T值最小的幂集作为设备均衡组的一部分。
由于方案2在确定均衡差△T时比方案1考虑的情况多,因此方案2的结果可能优于方案1。但由于方案2的时间复杂度是指数级的,而方案 1的时间复杂度在二次多项式内,考虑调度方法的实用性和时效性,针对工序设备分组中可调度工序大于等于3的情况时,选择方案1进行车间均衡。
3.2 工序车间确定策略
产品在两车间分布式加工制造,存在工序在两车间移动的情况,关于工序的移动提出以下相关概念:
定义 4(工序移动) 产品加工时,当工序 qi的紧前工序Fi与其不在同一车间,需将Fi的加工结果移动到qi所在的车间,称其为工序移动。
定义5(位移数) 由工序移动产生的次数称为位移数。
由于工序移动会增加产品完工的时间,当确定设备均衡组后,需确定设备均衡组 2个组合的加工车间,以减少位移数,于是根据工序相关性[14]提出分组工序车间确定策略。工序车间策略实现流程如图2所示。
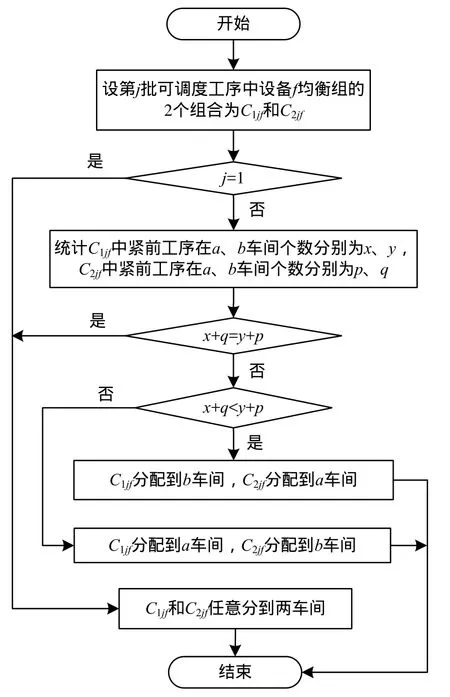
图2 工序车间策略实现流程
工序车间确定策略描述如下:
设第j批可调度工序中设备f均衡组的2个组合为C1jf和C2jf,对C1jf和C2jf中工序的紧前工序所在车间进行统计。设组合C1jf中工序的紧前工序在a、b车间的总数分别为x、y,组合C2jf中工序的紧前工序在a、b车间的总数分别为p、q。若C1jf组合中的工序在a车间加工,C2jf组合中的工序在b车间加工,则产生的位移数为y+p,反之产生的位移数为x+q。于是工序车间确定策略是选择产生位移数较少的将两组合分配到两车间的方式。即通过min{x + q, y + p}确定C1jf和C2jf所在车间;若x+q和y+p相等,即工序的紧前工序在两车间分布数相同,则任意分配两组合到两车间。
4 可调度工序分组处理的实现与分析
4.1 算法实现
为了实现产品在两车间分布式加工缩短产品完成时间和减少工序移动次数的目标,提出两车间可调度工序分组均衡处理的综合调度算法。该算法的主要思想是将原始叶节点工序和每次动态生成的叶节点工序分批处理,再将每批工序按设备加工时间尽量均衡地分为 2组,再将已分组的工序分配到其紧前工序个数较多的车间,对分组中的工序依次按序调度并在相应设备上确定尽早开始加工时间,最后修改当前已调度工序的紧后工序、紧前工序个数属性。
对可调度工序按批进行分配调度时,既考虑了可调度工序车间均衡又考虑了减少位移数,因此该算法可使产品尽早完成且控制工序位移次数。算法的描述如下:
(1)输入设备数和产品信息。
(2)根据工序 qi紧前工序个数属性 ei为 0确定可调度工序。
(3)根据上一批可调度工序在a、b车间中各设备完成时间 Ea(j–1)、Eb(j–1)的最大值,即 Sj=(Ea(j–1)≤Eb(j–1)?Eb(j–1):Ea(j–1)),确定每批可调度工序的开始加工时间Sj。
(4)可调度工序按设备进行分组。
(5)如果工序设备分组中工序数小于等于 2,将工序依次存入两组合,此时组合可以为空集;若分组中工序数大于2,依据车间均衡策略进行均衡分组。
(6)判断所有的工序设备分组是否达到车间均衡,不均衡则执行步骤(5)。
(7)判断可调度工序的批次j是否为1,若为1则转到步骤(9)。
(8)根据分组工序车间确定策略确定设备均衡组的加工车间,方法是对设备均衡组中的工序,根据已加工工序紧后工序属性 Li,依次寻找紧前工序并确定紧前工序所在车间 w,同时累加对应车间工序数,并根据工序数的多少确定设备均衡组的加工车间。
(9)各设备均衡组中的工序按序调度,且开始加工时间为Sj。
(10)判断此批可调度工序的紧后工序Li是否为空,为空转到步骤(14)。
(11)计算此批工序在两车间的结束时间Eaj和Ebj。方法是由问题描述中的式(3)有:Eaj=Sj–1+Taj或 Ebj=Sj–1+Tbj;根据式(6)有:Taj=max{Caj1,Caj2,…,Cajf,…,Cajm}或 Tbj=max{Cbj1,Cbj2,…,Cbjf,…,Cbjm}。
(12)修改此批可调度工序的紧后工序、紧前工序个数属性,配合完成下批可调度工序的确定。方法是对当前批次可调度工序的紧后工序、紧前工序个数依次进行减1操作。
(13)删除此批可调度工序,并将可调度工序的批次j值加1且转到步骤(2)。
(14)输出甘特图。
(15)结束。
算法流程如图3所示。
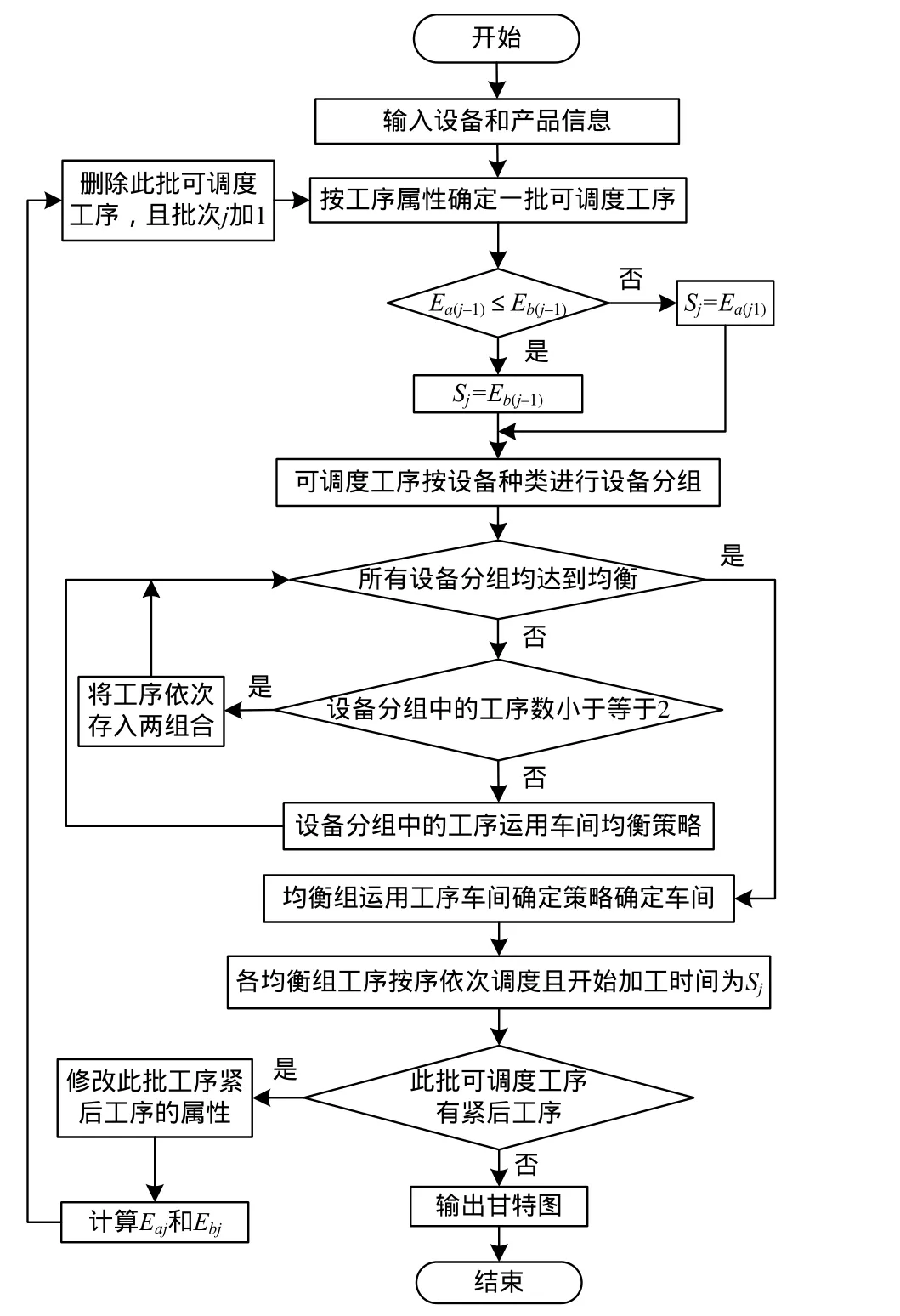
图3 本文算法流程
4.2 算法复杂度分析
本文算法特点是动态生成可调度工序,并按批进行调度处理,所以,下面针对一批可调度工序调度处理的复杂度进行分析。
(1)可调度工序确定。根据工序qi紧前工序个数的属性ei确定可调度工序,方法是当ei=0,qi为可调度工序。对n个工序需进行n次判断处理,所以,可调度工序确定的复杂度为O(n)。
(2)工序设备分组及排序。根据工序qi加工设备属性Mwi先进行工序设备分组,此时需判断 n次;然后进行工序设备分组中工序排序,设工序设备分组中每个设备工序数平均为 n/m,于是每个设备上工序升序排序的操作次数是,所有工序设备分组并排序的操作次数是 n+,由于1 ≤ m<<n,因此工序设备分组并排序的复杂度为O(n2)。
(3)车间均衡。工序设备分组中工序要达到车间均衡,对每个工序设备分组工序加工时间求和,再除以 2求得平均时间Pm,需运算n/m次;工序设备分组中的工序依次累加到D且与Pm比较,最多需计算和判断2n/m次;均衡差△T与G中工序,最多进行比较和调整次数为n/m+1。每个工序设备分组达到车间均衡的操作次数是4n/m+1。所有工序设备分组处理的次数为m(4n/m+1),因此,车间均衡的复杂度为O(n)。
(4)分组工序车间确定。若工序qi已加工调度,可通过工序属性Mwi确定其加工设备和加工车间。一批可调度工序得到的某设备均衡组中的工序数平均小于n/m,已加工工序最坏情况下为n。
确定设备均衡组中一个工序的紧前工序及紧前工序所在车间,需判断已加工的n个工序紧后工序属性n次,再确定其所在的车间最多n次,在累加车间工序数最多n次,所以确定设备均衡组中一个工序的紧前工序及紧前工序所在车间最多需处理3n次。
确定设备均衡组的组合中 n/m个工序的紧前工序及紧前工序所在车间最多需处理3n2/m次,于是一个设备均衡组分组工序车间确定的次数为6n2/m,所有设备均衡组确定车间的次数为6n2。因此,分组工序车间确定的复杂度为O(n2)。
(5)分组中工序的依序调度。设备均衡组的一个组中工序按序调度,由于平均每个组中工序个数小于n/m,组中工序需要比较的次数为,一个设备均衡组工序按序调度需比较次数为。因此所有分组中工序依序调度的比较次数为,即复杂度为O(n2)。
(6)工序紧后工序属性的修改。当前批次可调度工序个数最多为n,每个工序查找其紧后工序且紧后工序的紧前工序个数属性进行一次减 1操作。由于被查找的工序数最多为n,因此查找紧后工序的操作最多为n×n次,修改一批可调度工序的紧后工序紧前工序个数属性的修改次数最多为n。因此,修改一批可调度工序的紧后工序紧前工序个数属性的操作次数的数量级最多为O(n2)。
综上所述,在最坏情况下,对一批可调度工序调度处理的时间复杂度为O(n2)。设产品分k批调度,因此,本文算法复杂度应为O(kn2)。
5 调度实例
若有单件复杂产品A,其加工工艺树如图4所示,框内符号分别表示:产品的工序名|加工设备名|工序加工时间。
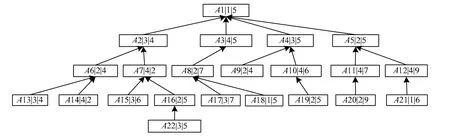
图4 产品A的加工工艺树
由工序紧前工序个数属性为0确定第1批可调度工序{A13, A14, A15, A22, A17, A18, A19, A9, A20, A21};根据定义 1进行工序设备分组且分组中工序 qi按加工时间属性 ti升序排序(Mf表示工序设备分组的工序组):M1{A18, A21},M2{A9, A19, A20}, M3{A13, A22, A15, A17}, M4{A14}。
M1组中两工序依次分配到两车间;M2组工序数大于2,需进行车间均衡,A9与A19的加工时间和与平均值Pm相等,所以设备均衡组两组合C112{A9, A19}、C212{A20};M3组工序(A13, A22, A15)累加和D首次满足大于Pm,即15>11时,两组合C113{A13, A22, A15}、C213{A17},均衡差值△T=D –Pm=4,△T与累加工序A13的加工时长相等,于是应调整到C213中,所以C213改为{A13, A17},C113改为{A22, A15},M4{A14}任意分配。
最后分到 a车间加工调度的工序{A18, A9, A19, A13,A17, A14},b车间加工调度的工序{A21, A20, A22, A15}。由于此批可调度工序无紧前工序,因此开始加工时间S1为0,对此批可调度工序进行加工调度。根据已加工工序可知此批可调度工序在a、b车间加工结束时间均为11个单位。
修改此批可调度工序的紧后工序、紧前工序个数属性,并删除此批可调度工序。根据工序、紧前工序个数属性 ei为0确定下一批可调度工序{A6, A16, A8, A10, A11, A12},按工序设备分组,分组中工序按加工时长升序排序M2{A6,A16, A8}、M4{A10, A11, A12}。
M2组进行车间均衡,A6和A16的加工时间和D与Pm的关系9>8,△T =D–Pm=1,△T小于累加工序中第1项,所以不需调整,最后组合C122{A6, A16}、C222{A8};M4组车间均衡后均衡组的两组合C124{A10, A11}、C224{A12}。
由于此批工序有紧前工序,因此需根据分组工序车间确定策略进行车间选择。首先统计两组合C122、C222中紧前工序在两车间的个数。C122、C222在a车间的个数分别为x=2、p=2,在 b车间的个数分别为 y=1、q=0;若组合 C122在a车间加工产生的位移数为1,C222在b车间加工产生的位移数为2,总位移数3;反之产生的总位移数2;选择位移数少的方式进行分配,即选择位移数为2的方式将C122分配到b车间,C222分配到a车间;同理C124分配到a车间,C224分配到b车间。
于是,此批分到 a车间加工的工序{A8, A10, A11},b车间加工的工序{A6, A16, A12}。此批工序的开始加工时间为上一批工序加工结束时间即11,调度此批可调度工序。由于Ta2为13、Tb2为9,因此Ea2为24、Eb2为20。
按照上面的处理方法对每批工序分配和调度直到最后一个工序处理结束,产品在a、b车间调度的甘特图如图5和图6所示。
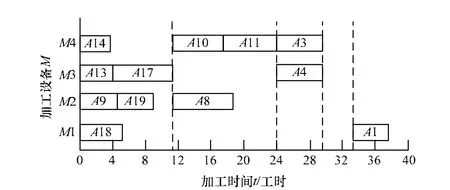
图5 车间a所得甘特图
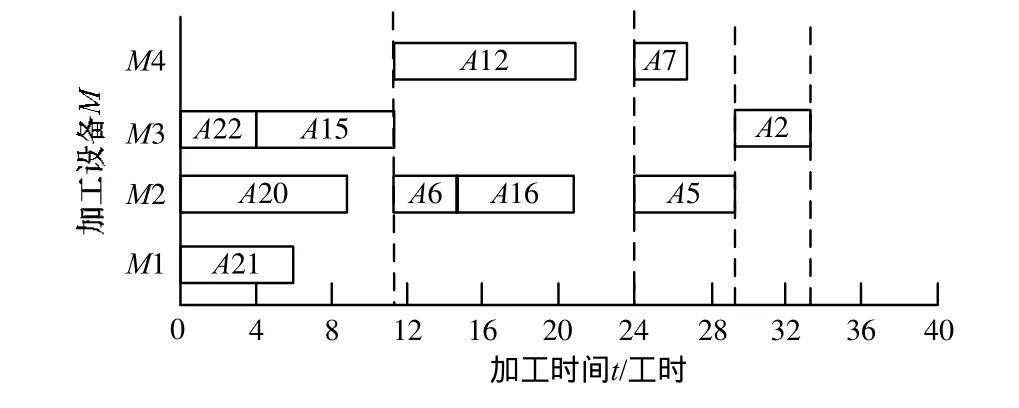
图6 车间b所得甘特图
若对每批可调度工序处理时不采用上文提出的策略,即先进行设备均衡处理,而是将工序降序排序后通过考虑设备均衡进行工序车间分配。
对第 1批可调度工序并按路径长度降序排序为{A20,A21, A17, A18, A22, A19, A13, A15, A14, A9}。依次将工序按尽早加工要求分配到两车间,分到 a车间的工序为{A14,A17, A15, A19, A9, A21}、b车间的工序为{A22, A13, A20,A18}。
依次类推得到该方法a和b车间产品调度甘特图如图7和图8所示。
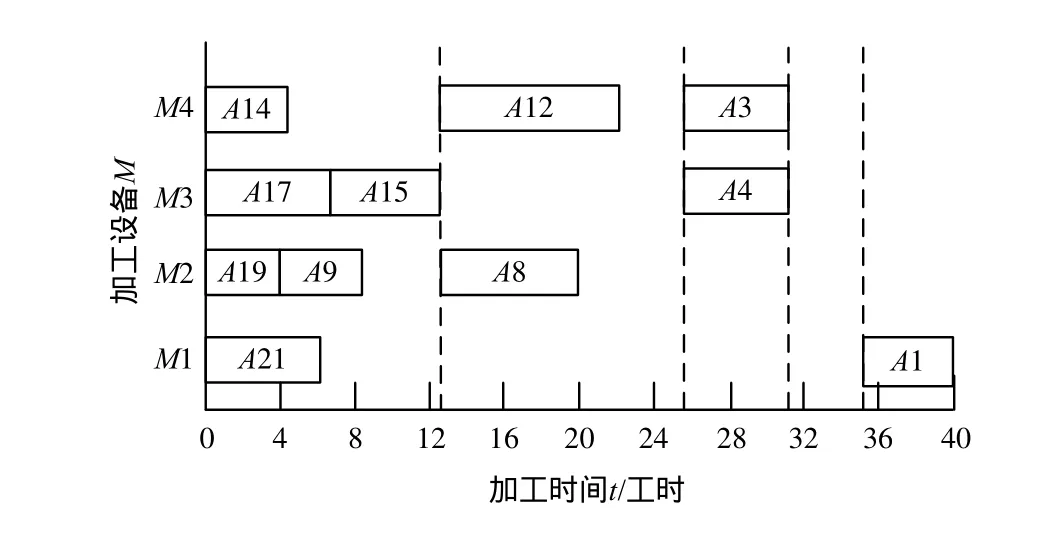
图7 对比方法所得a车间甘特图
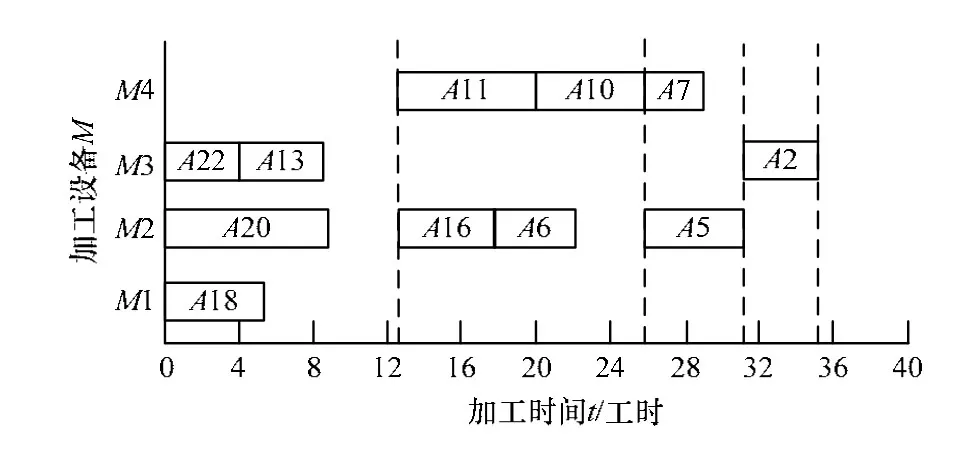
图8 对比方法所得b车间甘特图
由图5、图6与图7、图8对比可以看出,采用本文的算法产品加工完成时间是38工时,产生的位移数为6,采用另外一种方案的加工时间是40工时,产生的位移数为8。
之所以第1个方案效果更好,是因为第2个方案既没有真正地实现设备均衡,也没有考虑工序移动次数。例如,第1批结束时间方案1是11,而方案2是13。
6 结束语
针对单件复杂产品在两车间分布式制造问题,本文根据动态生成可并行处理的可调度工序和两车间的资源属性提出了 2个方案:设备均衡策略和工序确定车间策略,通过 2个策略的结合应用,实现了两车间分布式制造调度的综合调度。主要结论如下:
(1)按可调度工序分批处理,再按工序设备分组和车间均衡处理,算法简单,效果较好,且算法复杂度不超过二次多项式。
(2)按分组工序车间确定策略确定工序所在车间,减少了工序在两车间的移动次数,缩短了产品加工时间。
本文为解决具有相同资源的两车间分布式调度提供了解决方案,对研究多车间分布式综合调度问题有一定的借鉴作用。
[1]黄启春, 陈 奇, 俞瑞钊.一种面向作业的快速调度算法[J].软件学报, 1999, 10(10): 1073-1077.
[2]Brucker P, Sotskov Y N, Werner F.Complexity of Shop-scheduling Problems with Fixed Number of Jobs: A Survey[J].Mathematical Methods of Operations Research,2007, 65(3): 461-481.
[3]张维存, 郑丕谔, 吴晓丹.蚁群遗传算法求解能力约束的柔性作业车间调度问题[J].计算机集成制造系统, 2007, 13(2):127-131, 156.
[4]羌 磊, 肖田元.应用扩展贝叶斯进化算法求解混流装配调度问题[J].计算机集成制造系统, 2007, 13(2): 111-116.
[5]李 原, 张开富, 王 挺, 等.基于遗传算法的飞机装配序列规划优化方法[J].计算机集成制造系统, 2006, 12(2): 30-33.
[6]谢志强.工件间有约束的复杂产品工序调度研究[D].哈尔滨:哈尔滨理工大学, 2009.
[7]谢志强, 辛 宇, 杨 静.基于设备空闲事件驱动的综合调度算法[J].机械工程学报, 2011, 47(11): 139-147.
[8]谢志强, 李志敏, 郝淑珍, 等.工序间存在零等待约束的复杂产品调度研究[J].自动化学报, 2009, 35(7): 983-989.
[9]Xie Zhiqiang, Hao Shuzhen, Ye Guangjie, et al.A New Algorithm for Complex Product Flexible Scheduling with Constraint Between Jobs[J].Computers & Industrial Engineering, 2009, 57(3): 766-772.
[10]Xie Zhiqiang, Ye Guangjie, Zhang Dali, et al.New Nonstandard Job Shop Scheduling Algorithm[J].Chinese Journal of Mechanical Engineering, 2008, 21(4): 97-100.
[11]谢志强, 王 悦, 杨 静.存在批量为2的批处理设备的综合调度算法[J].北京工业大学学报, 2011, 37(10): 1470- 1476, 1481.
[12]谢志强, 杨 静, 杨 光, 等.可动态生成具有优先级工序集的动态Job-Shop调度算法[J].计算机学报, 2008, 31(3): 502-508.
[13]谢志强, 邵 侠, 杨 静.存在设备无关延迟约束的综合柔性调度算法[J].机械工程学报, 2011, 47(4): 177-185.
[14]熊禾根, 李建军, 孔建益, 等.考虑工序相关性的动态Job Shop调度问题启发式算法[J].机械工程学报, 2006, 42(8): 51-55.

