面向地图综合的矢量曲线弯曲识别研究
李朝奎,骆文芳,张 强,严雯英
(1. 湖南科技大学 地理空间信息湖南省工程实验室,湖南 湘潭 411201;2. 湖南科技大学 地球空间信息科学研究中心,湖南 湘潭 411201)
对于大部分GIS软件而言,数据多以矢量形式存在,矢量曲线的综合是地图制图综合非常重要的内容之一[1]。曲线综合的关键是在保持原曲线基本形态特征的情况下,删除那些次要的小弯曲,并同时保持弯曲特征转折点的精确性和不同地段弯曲程度的对比[2]。随着制图综合技术的不断发展,已经出现了各种各样的曲线化简算法[3-5],如D-P算法、Li-Openshaw算法和James算法等,这些算法都是通过保留某些相对重要的特征点而删除矢量曲线上的某些坐标点来进行化简的。然而矢量曲线并不仅仅是点的集合,它更是一种具有几何形态的地理要素的表达。因此,矢量曲线的化简综合不是简单的点的取舍操作,而应充分考虑曲线的弯曲特征,顾及曲线表达的地理语义。
曲线形态的基本结构单元划分方法很多,相对其他曲线结构单元,弯曲更易于被人们理解和接受,按弯曲单元进行曲线划分符合认知规律[6]。只要矢量曲线的弯曲结构描述清楚,线状要素综合则表现为由低层小弯曲到上层大弯曲的化简、合并、删除过程,从而能够保证曲线整体结构特征不被破坏,同时曲线低层细节又得到简化。本文对矢量曲线弯曲识别的几种常用算法进行介绍,并在Visual Studio 2008和ArcEngine 9.3基础上编程对各种识别算法进行实例验证。
1 矢量曲线弯曲识别方法
1.1 基于通视性的弯曲识别
通视性是指在一个简单弯曲内,第一个点到该弯曲上其他点的任一直线都与弯曲曲线不相割。基于通视性的弯曲算法描述为:设点i、j是曲线中任意点,存在i+1≤j≤n,其中点i为某段弯曲的起点,Li,j是点i与点j连接的线段,为对应的向量。在同一弯曲中,存在所有的,即它们的向量叉乘存在相同的方向性,即在同一弯曲中向量总会在向量和向量中间。当与具有不同的正负性时,表示点j 为当前弯曲的结束点和第二个弯曲的起始点,见图1。
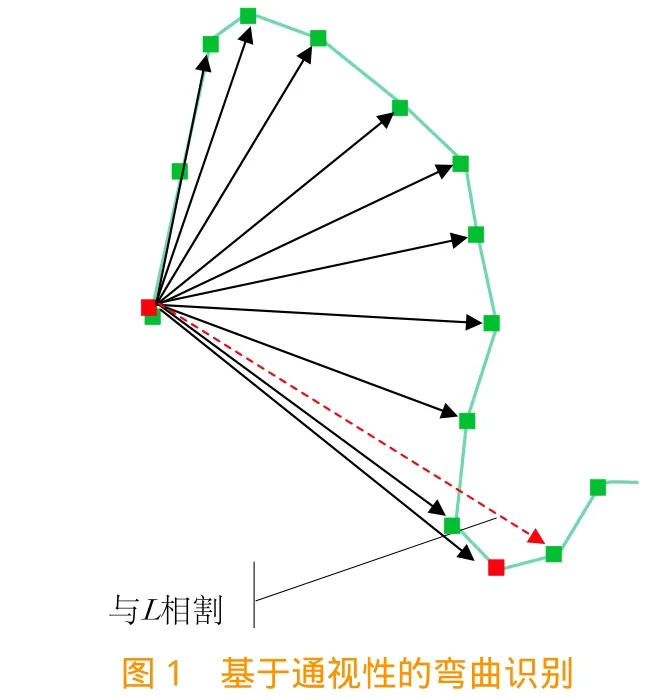
1.2 基于凹凸性的弯曲识别
基于凹凸性的弯曲识别方法分为以下几个步骤:①探查拐点;②将曲线起始点和所有拐点按其在曲线中的先后顺序依次放进分界点序列中;③根据分界点序列划分弯曲。其中,拐点的查找方法有以下两种:①通过边线上任一点向两边相邻的点作线段,两线段的张角小于180°,该点可认为是凸部点;大于180°,则是凹部点,等于180°,则该点处于平部。②曲线上点的切向绕行方向在拐点处发生变化。在拐点一侧为顺时针旋转,在另一侧则顺时针转,因而可以采用向量叉乘的方法来判断。其核心代码如下:
//构建向量
fv = new Vector(pnts[i–1], pnts[i]);
tv = new Vector(pnts[i], pnts[i+1]);
//向量叉乘结果是否大于0
flag = Vector.CrossProduct(fv, tv) > 0 ? true : false;
//如果当前向量叉乘结果与之前向量叉乘结果相异,则取当前点为特征点
if (curFlag != flag)
{
if (pntCol.PointCount> 2)
{
(bend as IriverLine).Polyline = pntCol as Ipolyline;
bends.Add(bend);
featPnts.Add(pnts[i]); //添加特征点
bend = new Bend();
pntCol = new PolylineClass();
pntCol.AddPoint(pnts[i].ToEsriPoint(),ref missing, ref missing);
}
curFlag = flag;
}
1.3 基于曲率极大值的弯曲识别
基于曲率极大值的弯曲划分方法如下:首先,计算点pi-1和点pi的切线角αi-1和αi;其次,计算由点pi-1和点pi组成的直线段li-1,i的长度;再次,求取点pi-1和pi的平均曲率ki-1,将ki-1作为点pi-1的曲率;最后,按照上面的方法依次计算每个点的曲率,算出所有曲率极大值(绝对值),如图2所示。其核心代码如下:
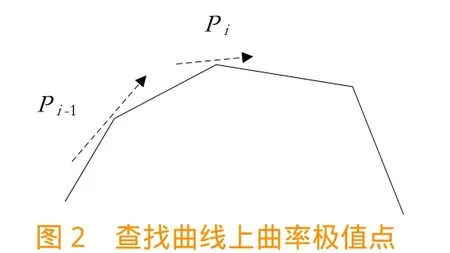
//求当前点与前一点的平均曲率
Cur = Math.Round(Math.Abs(pnts[i].Tangent -pnts[i - 1].Tangent) / PointUtil.GetDistance(pnts[i], pnts[i- 1]),5);
flag = forCur> Cur ? false : true;//与之前的平均曲率的大小对比
forCur = Cur;
//如果当前曲率对比为否,之前曲率对比为真,也就是曲率极大值所在
if (curFlag&& !flag)
{
//第i-1个是极大值,添加特征点
featPnts.Add(pnts[i -1]);
//生成弯曲
IPointCollection polyline = new PolylineClass();
for (int j = startIndex; j < i; j++)
{
polyline.AddPoint(pnts[j].ToEsriPoint(), ref missing,ref missing);
}
(bend as IRiverLine).Polyline = polyline as IPolyline;
bends.Add(bend);
//重新初始化
bend = new Bend();
startIndex = i - 2;
}
curFlag = flag;
2 实例验证
实例设计的目的是通过实践来查找弯曲特征并检验各种弯曲识别方法的可行性,从而分析各种识别方法的优缺点。该实验以矢量曲线为例,在Visual Studio 2008和ArcEngine 9.3基础上编程实现。
2.1 基于通视性的弯曲识别
根据前文算法,得到如图3所示的结果。可以看出,这种弯曲识别方法存在着一个极大的优点,就是能在弯曲划分之后,较为轻松地判断弯曲的类型是U型还是V型。但在弯曲分布不匀称或不理想的情况下,它也存在某些缺点,如弯曲划分不匀称、效果不好。具体表现在,在视觉上应为V型或者U型的弯曲,没有全部划分出来。在弯曲分布不均匀的曲线上,划分出的复杂弯曲和简单弯曲在长度上差距较大。
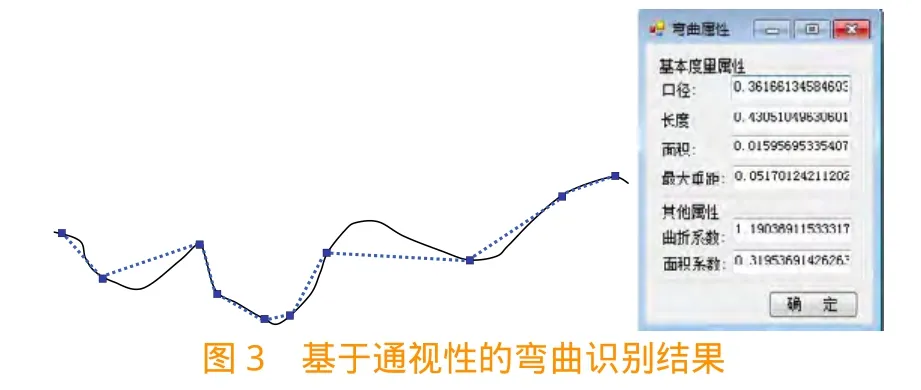
2.2 基于凹凸性的弯曲识别
根据拐点划分弯曲是运用最广的方法。通过图4可以看出,此方法的优点是十分明确地区分了曲线的凹部和凸部,即凹凸的弯曲按顺序均匀地分布在拐点连线的左右。但也存在着许多缺点,如小弯曲(长度小)、微弯曲(弯曲度小)也被划分为弯曲。

2.3 基于曲率极大值的弯曲识别
通过此方法得到的弯曲大多数情况下是简单弯曲,如图5所示。

从上述实验中可以看出,基于通视性的弯曲识别其结果不是很均匀,其中既包括复杂弯曲,又包括简单弯曲。弯曲的弧底点在曲折系数较大的弯曲上较为突出,在曲折系数小的弯曲上表现不突出。基于凹凸性的弯曲识别其结果比较均匀,视觉效果比较理想。基于曲率极大值点的弯曲识别方法所探查到的曲率极大值点很多,超出了我们视觉上所认为的曲率极大值点数,比基于凹凸性弯曲识别方法的结果更加细腻。此外,其划分的弯曲都是简单弯曲。
3 结 语
线要素化简的基本要求是整体轮廓形态的保持,尤其是每段大弯曲的特征点和形状的保持,而根据不同的需要利用以上识别方法之一对矢量曲线进行弯曲识别后再对曲线进行化简,有利于线要素整体形状的自然保持,也可使化简综合的结果更合理。本文从理论和实践的角度对比了几种弯曲识别方法的合理性和优缺点,为地图综合中矢量曲线的化简提供了质量保障。
[1]王结臣,闾国年.曲线矢量数据综合的微凹凸消除算法[J].测绘通报,2002(1) : 17-18
[2]Wang Jiayao. The Principle of Cartographic Generalization for General Map[M].Beijing: Publishing House of Surveying and Mapping, 1993
[3]Douglas D H, Pecuker T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. The Canadian Cartographer, 1973,10(2):112-122
[4]Mamaster.Automated Line Generalization[J].Cartographica,1987,24(2):74-111
[5]Li Zhilin, Openshaw S. Algorithms for Line Generalization Based on Natural Objective Principles[J]. International Journal of Geographic Information Systems, 1992,6(5):373-389
[6]Wang Z, Muller J C. Line Generalization Based on Analysis of Shape Characteristics [J].Cartography and Geographic information Systems.1998, 25 (1):3-15
[7]钱海忠,伍芳.采用斜拉式弯曲划分的曲线化简方法[J].测绘学报,2007,36(4):443-449

