焊接残余应力对十字防屈曲支撑内芯屈服行为的影响

江余东，周广涛，王立鹏，牛济泰

（1.华侨大学机电及自动化学院，厦门 361021；2.河南理工大学材料科学与工程学院，焦作 454000）

0 引 言

防屈曲支撑是通过钢材的拉压塑性变形消耗结构振动能量的一种位移相关消能器［1］，主要用于建筑结构耗能减震设计，承受地震引起的侧向拉压载荷，近年来在国内外尤其是在日本和美国的研究与应用逐渐增多［2］。防屈曲支撑由钢内芯、外包约束构件、两者之间的无粘结层或间隙及内填材料四部分［3］构成。

由于全钢防屈曲支撑具有质量小、加工简便、安装便捷等优点，且具有明显的抗震效果，在地震多发的日本应用广泛［4－7］。钢内芯通常为十字形和一字形。一字形有缺陷，而十字截面的型钢没有市售，通常用三块钢板相互焊接而成。由于焊接的整体性较差，因此，十字型内芯在实际应用中还存在颇多问题［8］。

传统的防屈曲支撑内芯的设计方案都未考虑到焊接残余应力的影响，导致内芯的设计性能与实际性能有很大偏差，使防屈曲支撑在所预计的地震强度（拉压载荷）下不能发生屈服以消耗结构振动能量，进而影响结构的实际抗震性能。目前，对全钢防屈曲支撑构件的试验研究较多［9－12］，文献［13］的结果表明这类支撑的实测屈服轴向力与设计屈服轴向力相差约40%，同时由于焊缝的屈服强度一般比芯材的屈服强度高，导致该类支撑的实测性能与设计性能有显著差异。因此，研究焊接残余应力对支撑内芯性能的影响有重要意义。

为此，作者针对十字形全钢防屈曲支撑内芯，从焊接角度分析、修正该结构设计方案，以理论推导的方式着重分析了焊接残余应力对受交变载荷作用下内芯的应力变化，并应用有限元方法对十字形截面支撑内芯进行焊接残余应力场分析及承受轴向拉压载荷下的应力场分析，研究其屈服行为，为防屈曲支撑结构的优化设计及工程应用提供参考依据。

1 防屈曲支撑内芯的结构

支撑内芯由一块芯板和两块加筋板焊接而成，其结构如图1所示。其中芯板采用整体火焰切割得到，其基本尺寸如图2所示。

图1 内芯结构Fig.1 The structure of the inner core

图2 芯板尺寸Fig.2 Dimension of the inner core plate

防屈曲支撑的性能主要取决于内芯的强度，内芯受轴向载荷作用时，内芯轴向变形，由于应力分布不均，在某些应力集中的地方先发生塑性变形，达到屈服状态，起到抗震耗能的效果。

2 有限元模型的建立

采用有限元模拟软件MSC.Marc按照十字形内芯的实际尺寸建立有限元模型，选择八节点四面体单元（QUAD8）进行网格划分，按照靠近焊缝区域单元密集、远离焊缝区域单元稀疏的原则划分网格，划分后十字形内芯模型的节点数为74 805个，单元数为64 864个。十字形截面防屈曲支撑内芯的材料全部采用Q235钢，Q235钢的基本材料参数见表1。十字形内芯的有限元模型如图3所示。

表1 Q235钢的基体参数［1］Tab.1 Basic parameters of the Q235steel

图3 十字形内芯的有限元模型Fig.3 Finite element model of the cross shape inner core

焊接残余应力的大小由温度场决定，为确保焊接温度场模拟结果的准确性，使分析结果更准确，采用双椭球热源模型［14］。

前半椭球热源表达式：

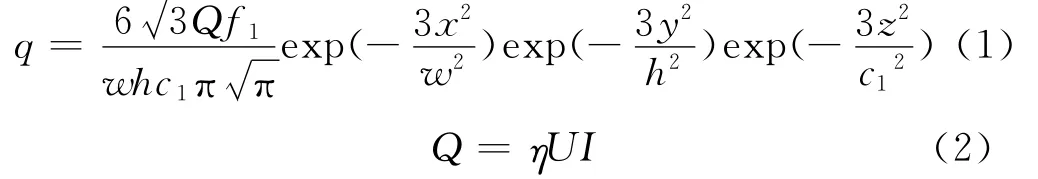
后半椭球热源表达式：

式中：η为热源效率；U 为焊接电压，V；I为焊接电流，A；w为热源半宽；h为热源深度；c1为前半球长度；c2为后半球长度；f1，f2为前后椭球热量分布函数，f1＋f2＝2。

采用热－力耦合来模拟焊接过程，整个模拟过程分为两部分，首先模拟焊接过程，即将加筋板焊接到芯板的过程，得到焊接残余应力分布场；待散热完全后（达到室温），在内芯两端施加均匀的轴向拉压载荷，加载时间为1 000ms，模拟其在焊接残余应力的作用下，内芯处于拉压状态时，屈服段应力的分布及变化情况。

3 计算结果及分析

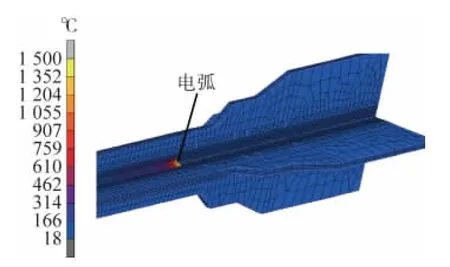
图4 焊接进行到第509s时内芯温度场的分布Fig.4 Temperature distribution in the inner core at the 509th second in welding process

对内芯有限元模型进行计算分析，得到焊接过程中的温度场及焊后焊接残余应力分布云图。由图4可知，在焊接进行到第509s时，内芯电弧处的温度最高，达1 500℃，达到金属材料的熔点，表明焊接参数设置正确。

从图5中可以看出，在焊接结束后，最大残余应力区为颜色最亮的部分，即内芯截面的中心区域（Ⅰ区域）。在此区域，残余应力的最大值可达288MPa，平均应力约为240MPa，已经达到了材料的屈服强度（235MPa）。

图5 内芯横截面上纵向焊接残余应力的分布云图Fig.5 Welding residual stress contours along longitudinal direction within the cross-section of the inner core

从图5还可以看出，纵向焊接残余应力的分布规律为，靠近焊缝处的焊接残余应力为拉应力，且均达到了材料的屈服强度，远离焊缝处为压应力，且在截面上拉、压应力保持平衡，截面上的应力分布及大小如图6（a）所示。结构在纵向受拉、压载荷时，截面上的应力会随着载荷发生相应的变化，如图6（b），（c）所示。设加载前焊缝及其附近区域处的焊接残余应力为σ1，受拉后为σ′1，受压后为σ″1，远离焊缝处的残余应力为σ2，受拉后为σ′2，受压后为σ″2，σs是材料的屈服强度，σp是载荷P产生的应力，b是σ1＝σs区域的宽度，即图6（a）中内芯截面的剖面部分，t为内芯的板厚，B是板的宽度。截面中的剖面区域为应力已经达到屈服强度的部分。

图6 内芯在纵向受拉、压载荷前后的应力分布Fig.6 Stress distributions in the inner core before loading（a）and on a tensile loading（b）or a compression loading（c）

由于十字形内芯由钢板焊接而成，且钢板足够长，因此，满足平面假设原理：即当承受轴向载荷时，内芯的平截面始终保持为平面。根据图6（a）所示的应力分布情况，设焊脚尺寸为k，应用焊接结构学相关知识得［15］：

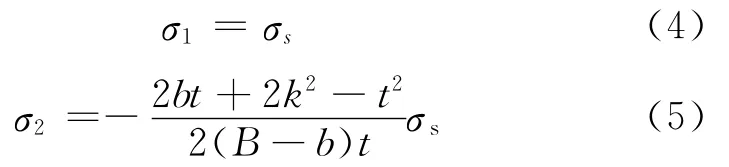
结构在承受拉、压载荷时，在不考虑焊接残余应力的情况下，要使内芯屈服，轴向拉伸与轴向压缩所需要的载荷大小是一样的，理论设计载荷为P。

由于t2很小，为计算方便将其省略，于是由式（5）和（6）得到：

当考虑焊接残余应力时，将分拉伸与压缩两种情况讨论。

（1）内芯承受拉伸载荷

施加拉伸载荷时，外载荷引起的拉应力与焊接残余应力叠加，受焊接残余应力的影响，焊缝及其邻近区域内（中心区域）的拉应力已达到屈服强度，因此该区应力不再增大，丧失进一步承受外力的能力，这样就相当于削弱了内芯构件的有效面积，施加的拉伸载荷全部由焊缝及其邻近区域以外的区域（即非中心区域）承担，直到其应力值达到屈服强度。当施加拉伸载荷P1时，局部屈服区应力保持不变，仍为σs，未屈服区应力则随着载荷的增加而不断增大，增加到σs时开始屈服并耗能，最终达到截面整体屈服。由此可得：

由于非中心区域的残余应力很小，可以忽略。要使此区域屈服，则

由以上推导可以看出，考虑焊接残余应力时内芯所能承受的实际载荷小于理论设计载荷，即内芯在较小的载荷下即开始发生局部屈服，并开始耗能。实际载荷与设计载荷的偏差可由式（14）计算。

（2）内芯承受压缩载荷

施加压缩载荷时，外载荷引起的压应力与焊接残余应力叠加，中心区域的焊接残余应力为拉应力，与压应力方向相反，而非中心区域存在焊接残余压应力，但还未达到屈服强度，因此，压缩载荷由内芯的整个截面积承受。随着载荷的增加，中心区域的拉应力逐渐减小，非中心区域的压应力不断增大，直到此区域发生屈服并耗能，即内芯在压缩载荷作用下先在非中心区域发生局部屈服耗能，继续加载才会使整体屈服。

设内芯承受的实际压缩载荷为P2，则

要使非中心区域发生屈服，则有

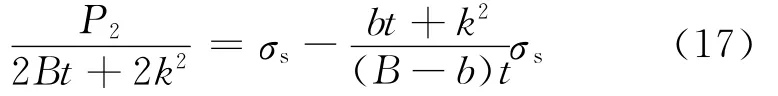
因此

由以上分析可知，考虑焊接残余应力时，内芯发生局部屈服时所承受的压缩载荷小于设计时的理论压缩载荷，再继续加载，内芯才会整体屈服。当内芯局部屈服时，实际压缩载荷与设计压缩载荷的偏差可由式（20）算得。

4 试验验证

根据相似理论，按比例缩小后得到十字内芯的拉伸性能与实际尺寸的十字内芯（见图1）是接近的。为此，实际焊接一个缩小后的十字内芯试样，试样板厚6mm、芯板尺寸为200mm×80mm、筋板尺寸为200mm×40mm、焊脚尺寸为5mm，并在岛津万能材料试验机上进行拉伸试验，拉伸加载速率为5N·s－1。内芯试样的拉伸曲线如图7所示，可以看出，受纵向焊接残余应力的影响，十字内芯试样的屈服强度为185MPa，小于材料本身的屈服强度235MPa。不考虑焊接残余应力时的理论设计载荷为235MPa。

图7 十字内芯的拉伸应力－应变曲线Fig.7 Tensile stress and strain curve of the cross inner core

由式（8）计算得到，内芯受拉发生屈服时的理论设计载荷P为260.85kN，而承受拉伸载荷时使内芯发生屈服的实际拉伸载荷P1为205.35N；由式（13）得ΔP为55kN，由式（14）得＝21.28% 。

由以上计算可知，受焊接残余应力的影响，十字形内芯发生屈服时所承受的拉伸载荷与理论设计载荷存在一定的偏差，验证了理论推导结果的正确性。

5 结 论

（1）由有限元分析结果可知，受焊接工艺的影响，十字形内芯存在焊接残余应力，焊缝及其附近区域处为拉应力，远离焊缝处为压应力；焊缝及近缝区处的拉应力达到了材料的屈服强度。

（2）当承受轴向载荷时，由于焊接残余应力的影响，内芯局部（受拉时在焊缝附近，受压时在远离焊缝区）先发生屈服，此时内芯所承受的拉伸载荷及压缩载荷均小于设计值，继续加载，达到一定值时内芯才会整体屈服。

（3）由于纵向焊接残余应力的存在，试验证明十字形内芯发生屈服时所承受的拉伸载荷与理论设计载荷存在较大偏差，达到21.85%。

［1］B 50011－2010 建筑抗震设计规范 ［S］.

［2］王凤欣，陈银，王高峰，等.屈曲约束支撑研究进展综述［J］.河北工程大学学报，2012，29（4）：28-36.

［3］赵瑛，郭彦林.防屈曲支撑框架设计方法研究［J］.建筑结构，2010，40（1）：38-85.

［4］王华琪，丁洁民，何志军.防屈曲支撑的应用与设计［J］.结构工程师，2007，23（4）：6-11.

［5］汪家铭，中岛正爱.屈曲约束支撑体系的应用与研究进展（I）［J］.陆烨，译.建筑钢结构进展，2005，7（1）：1-12.

［6］XIE Q.State of the art of buckling restrained braces in Asia［J］.Journal of constructional steel research，2005，61：727-748.

［7］杨昌民，牧野俊雄，李宏男.屈曲约束支撑的研究进展及工程应用［J］.建筑科学与工程学报，2011，28（4）：75-85.

［8］汪家铭，中岛正爱.屈曲约束支撑体系的应用和研究进展（Ⅱ）［J］.建筑钢结构进展，2005，7（2）：2-11.

［9］WAKABAYASHI M，NAKAMURA T.Experimental study on the elasto-plastic behavior of braces enclosed by precast concrete panels under horizontal cyclic loading：parts 1and 2［C］//Summaries of Technical Papers of Annual Meeting.［S.l］：Architectural Institute of Japan，1973：1041-1044.

［10］KIMURAK，YOSHIZAKI，TAKEDA T.Tests on braces encased by mortar in-filled steel tubes［C］//Summaries of Technical Papers of Annual Meeting.［S.l］：Architectural Institute of Japan，1976：1041-1042.

［11］FUJIMOTO M，WADA A.A study on the unbonded brace encased in buckling-restraining concrete and steel tube［J］.Journal of Structural and Construction Engineering：B，1988，34：249-258.

［12］严红，潘鹏，王元清，等.一字形全钢防屈曲支撑耗能性能试验研究［J］.建筑结构学报，2012，33（11）：142-149.

［13］闫鹏飞，吴运新，廖凯.切割对铝合金板厚残余应力分布影响的仿真与分析［J］.中南大学学报，2010，41（6）：2214-2217.

［14］GODAK J，CHAKRAVACHI A，MALCOLMB，et al.A new finite model for welding heat source［J］.Metallurgua Transactions，1984，15（2）：299-305.

［15］方洪渊.焊接结构学［M］.北京：机械工业出版社，2008.