双Buck逆变器的双环滑模控制策略

侯世英，邹学伟，张立帅，陈剑飞

（重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

随着化石能源的日益枯竭与环境污染的不断加剧，利用可再生能源进行发电已受到人们的广泛关注，而在可再生能源发电系统中起电能变换作用的逆变器是不可或缺的一部分。双Buck逆变器由于其克服了传统桥式逆变器的功率管直通、开关损耗等问题也越来越受到青睐，其拓扑结构和控制策略也成为一个研究热点［1-5］。

目前，基于电流滞环控制的外环电压内环电流双闭环控制方式已成为变换器领域内应用最广泛的控制策略之一［6-8］。滞环电流控制是一种典型的非线性控制方法，具有简单易于实现、可靠性高、稳定性好等优点；而采用双环控制方式，电压外环可实现稳压控制、减少波形畸变，电流内环可提高系统的动态响应和限流能力。然而，有学者发现将电流滞环型双环控制方式应用到双Buck逆变器［9-12］存在稳态精度不够高和带负载能力差的缺陷。文献［10］在对双Buck逆变器进行小信号分析和建模的基础上，发现系统的电压调整率随负载增大而增大，引入一种带谐振控制器的瞬时电压电流反馈双环调节方式，克服了其外特性较软、稳态精度难以满足要求的不足。文献［11］则采用自适应滞环电流控制策略克服滞环控制下双Buck逆变器开关频率不固定导致损耗大、输出电压谐波频率范围广的缺点，且在电压外环中采用数字PID控制和重复控制相结合的复合控制策略，改善了系统动态特性。而滑模控制的主要优点就在于可以保证系统在参数不确定情况下的稳定性和鲁棒性［13-16］，因此，为改善双Buck逆变器的带负载能力和稳态精度，本文提出一种基于滑模控制的双环控制策略，并对系统进行滑模控制器设计，对比分析传统的双环控制策略和双环滑模控制策略的优缺点，仿真与实验结果验证了理论的正确性。

1 双Buck逆变器双环滑模控制策略的提出

1.1 传统双环控制策略

图1为双Buck逆变器的主电路图，其中Ud为输入电源，uo为输出电压（电容电压 uC=uo），iL1、iL2分别为滤波电感L1、L2的电流，io为负载电流。当uo＞0时，VT2、VD2关断，VT1、VD1调制工作；当 uo＜0 时，VT1、VD1关断，VT2、VD2调制工作。

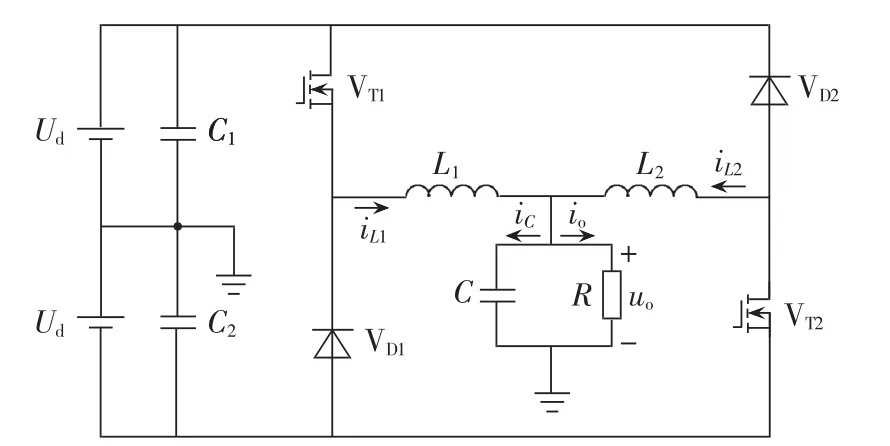
图1 双Buck逆变器主电路图Fig.1 Main circuit of dual-Buck inverter

双Buck逆变器传统双环控制策略等效框图如图 2（a）所示，将电流内环线性化后得到图 2（b）所示的逆变器系统控制框图［10］。

根据图2（b）可以得到系统闭环传递函数如下：

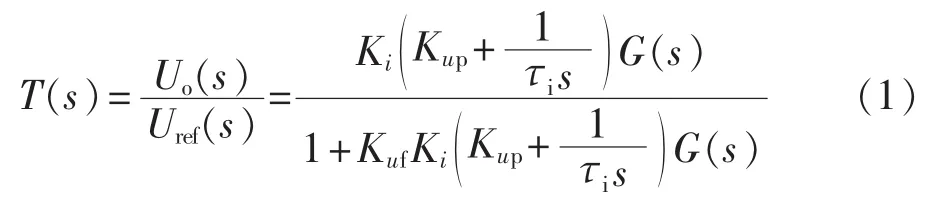
当输入量 uref（t）=Urefsinωt时，系统输出 uo（t）=，可以得到阻性负载时系统由空载加至满载的电压调整率［10］（即负载变化时输出电压的相对变化量 ΔU=（U1-U2） /U1×100%）：

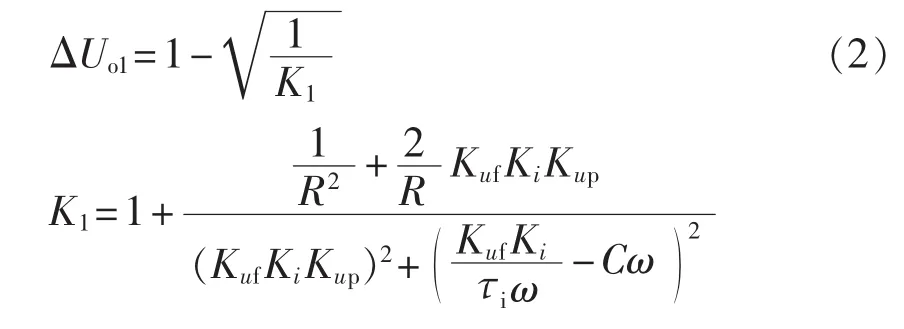
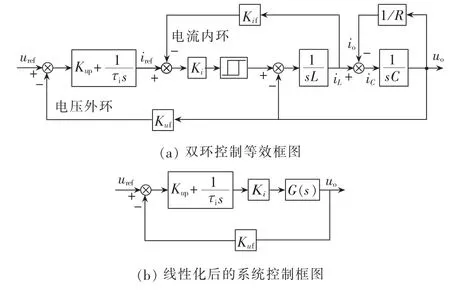
图2 双Buck逆变器传统双环控制策略Fig.2 Traditional double-loop control of dual-Buck inverter

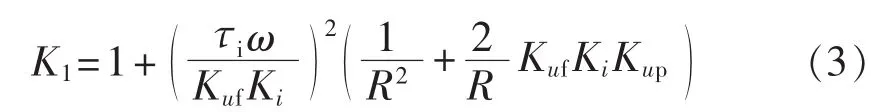
可以发现：τi、ω 越大，Kuf、Ki、Kup越小，则 ΔUo1越大，表明系统带负载能力与双环控制策略的参数设置有关。因此，研究双Buck逆变器的控制策略对其动态性能和稳压精度都具有重要意义。

1.2 双环滑模控制策略

滑模控制作为一种非线性控制方法，具有对参变量和外界干扰的强鲁棒性、良好的动态和稳态响应。通过上文分析，结合双环控制方法，本文提出一种基于滑模控制的双环控制策略，使系统既有双环控制的优势，又兼具滑模控制的特点。

对双Buck逆变器而言，其由2组Buck变换器独立工作，可得其每半个周期下的等效电路如图3所示，其中 L=L1=L2，开关量 u为开关 VT1的控制律，Uref、Iref分别是输出电压和电感电流的参考量，并且Iref是输出电压反馈量与电压基准比较后经PI调节得到，即 Iref= （Uref-uo）［Kup+1 /（τis）］。

选取输出电压误差x1及其动态误差x2、电感电流误差x3为状态变量，得到Buck变换器状态空间方程为：

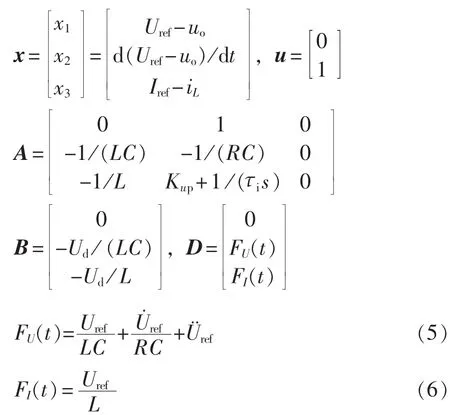
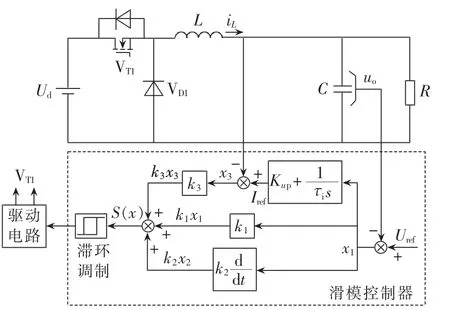
图3 双Buck逆变器等效电路Fig.3 Equivalent circuit of dual-Buck inverter

故Buck变换器状态方程可定义为：

从图3可知，滑模控制的电流内环也是与内环参数的选取相关的。由现代控制理论，系统的状态反馈（x3）和输出反馈（x1、x2）都不改变原系统的能控性，表明本文所选取的状态变量在理论上是可行的。

对双环滑模控制策略进行稳态精度分析，线性化后的等效控制框图如图4（a）所示，将图中分支点和综合点进行移动，同理对电流内环进行线性化处理，得到如图4（b）所示的双环滑模控制等效框图。

由图4（b）可以得到系统闭环传递函数：

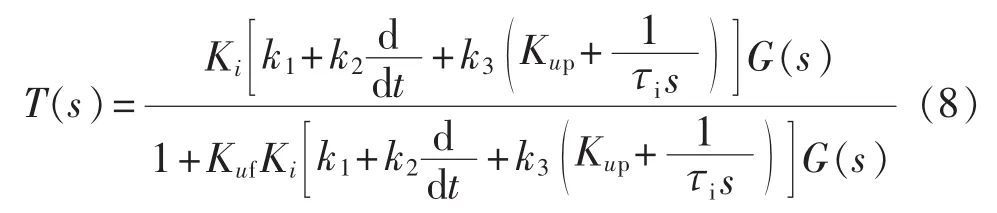
同理，可以得到阻性负载的电压调整率：

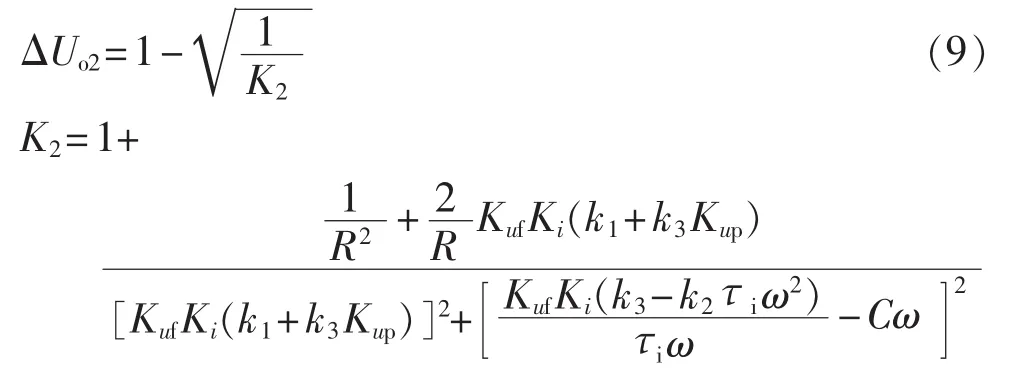
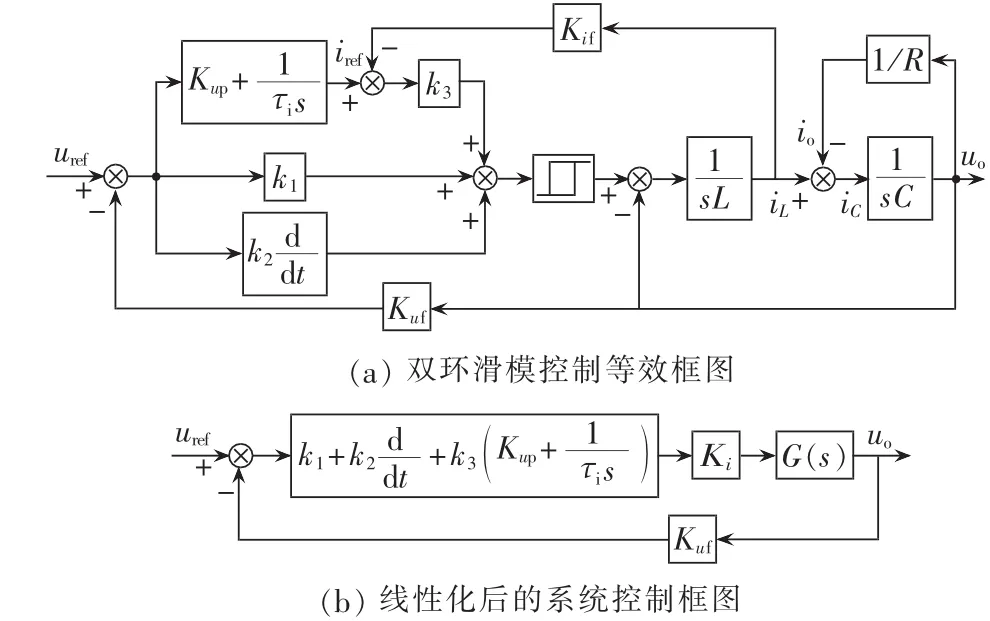
图4 双Buck逆变器的双环滑模控制策略Fig.4 Double-loop sliding mode control of dual-Buck inverter

对比式（2），由于 k1、k2、k3为正常数，使得不能将K2化简成式（3）的形式，但是可以得到：通过对k1、k2、k3取值的不同，可以使得在τi、ω、Kuf、Ki、Kup相同情况下，式（9）中的ΔUo2比式（2）的 ΔUo1小，即双环滑模控制下的系统稳态精度较双环控制的高。

2 滑模控制器设计

本文在分析双环控制双Buck逆变器的基础上，用滑模控制环节替代影响系统动态性能的电压电流环节，其双环滑模控制器如图3所示，其滑模面的选择为：

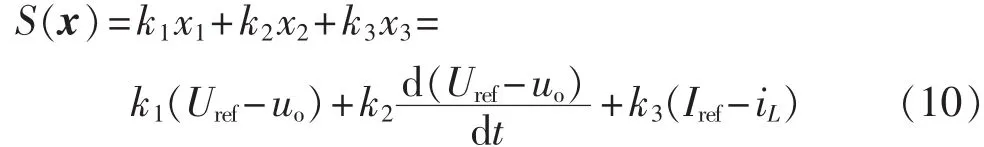
其中，k1、k2、k3均为正常数。式（10）可表示为：

其中，kT=［k1，k2，k3］为滑模面系数。

开关VT1的滑模控制律为：

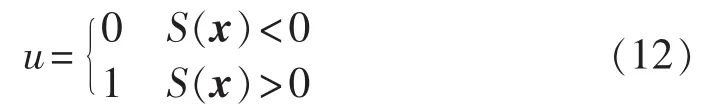
根据滑模控制理论，为了确保轨线保持于滑动线上，系统必须遵守由李雅普诺夫第二方法推导出的存在条件，它决定了系统的渐近稳定性，即：

于是，将式（11）对时间求导后代入上式，可得到滑模控制的存在和到达条件为：

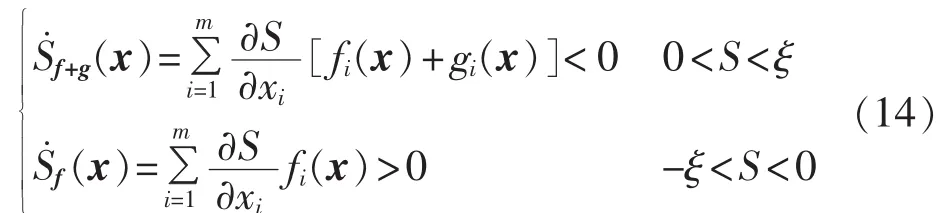
其中，ξ为任意小的正数。则滑模面S（x）上存在滑模运动的必要条件是：

将式（4）和（10）代入式（15）得：

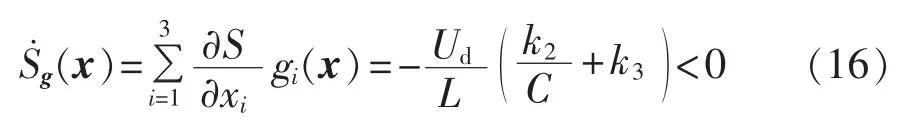
由式（16）知，S（x）满足存在滑模运动的必要条件。

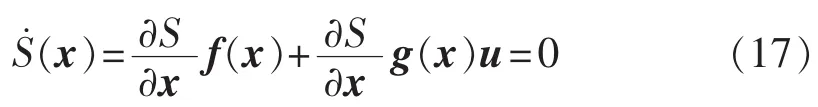
故可得到等效控制ueq为：

对于双Buck逆变器，滑模面上存在滑模运动的充要条件是：0＜ueq＜1。

滑模面函数S（x）中，k1和k2分别代表系统稳态和动态调节特性，即k1/k2值越大，系统的动态性能越好；k3为电流环的调节系数，代表了滑模面函数的电流调节性能。就双Buck逆变器而言，取k1=1、k2=k3=RC是比较合理的。当系统处于稳态时，Uref≈uo、Iref≈iL，因此可化简式（18）得：

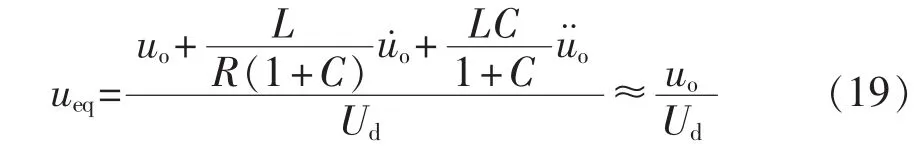
实际电路中L和C取值较小、R取值为欧姆级，且双 Buck 逆变器中 uo＜Ud，所以由式（19）可知：0＜ueq＜1，满足滑模切换面的存在和达到条件。

将式（18）代入状态方程（4）中，得：

根据李雅普诺夫稳定性原理，要使系统在滑模面上渐近稳定，A*的特征值具有负实部，则必须满足：

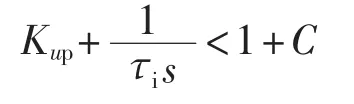
由上式可知，只要选择适当的PI参数就可以使得系统在滑模面上保持稳定的滑模运动。

理想的滑模控制系统完全运动于滑模面上，其开关频率是无限高的，由于实际的开关管频率有限，本文是采用滞环来限制开关频率，图5为滞环控制时系统状态轨迹的运行方式。设滑模面函数切换的滞环宽度为 2σ，滑模面等效导数（结合式（14）知可以估算出时间 t1和 t2：

则开关频率为：

将式（10）和式（14）代入上式并整理得：

可见，开关频率是随系统工作点变化而变化的，通过式（22）可以比较准确地估算出系统的开关频率，对滤波器参数的设计也具有重要的意义。

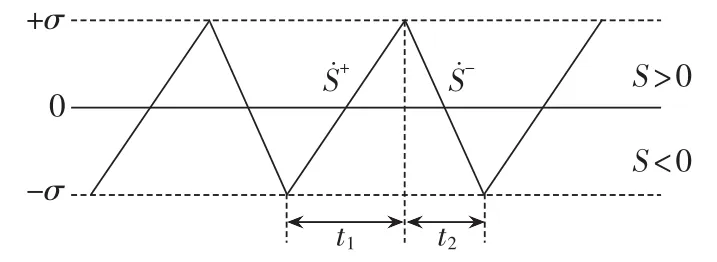
图5 滞环控制的滑动过程Fig.5 Sliding process of hysteresis control

3 仿真分析

为了验证上述所提双环滑模控制策略的正确性和可行性，在MATLAB/Simulink中建立了电路模型进行仿真分析。电路仿真参数设置如下：直流输入电压 Ud=120 V，电感 L1=L2=2 mH，电容 C=10 μF，负载R=10 Ω，输出电压参考值Uref为60 V、频率为50 Hz。控制器中滞环宽度2σ=1.6，PI的参数为KP=Kup=0.8、KI=1/（τis）=0.1。结合前文的理论分析，取上述参数时，式（2）中的 K1≈1.27，式（9）中的 K2≈1.02，可得 ΔUo1＞ΔUo2，即取上述仿真参数时，双环滑模控制策略的稳压精度比双环控制的高。

图6为双环滑模控制策略下系统稳态时的输出电压和输出电流波形。图7是输出电压的频谱图，可以发现输出电压谐波得到了很好的抑制，THD=0.46%，总谐波畸变率小，系统的稳态性能好。图8为电感电流iL1、iL2的波形，图9为开关管VT1和VT2的驱动信号，即系统的开关频率。从图8和图9（a）可知逆变器工作于半周模式，与前文分析系统工作原理一致；图 9（b）为 0.0435～0.047s之间开关管 VT1的驱动信号Ugs1，可以发现开关频率是不固定的，最高频率可达到200 kHz，最低频率约为30 kHz，将系统参数代入式（22）可以大致计算出系统开关频率在11.6～280.7 kHz之间，表明系统在工作时不可能达到理论分析时的极值工作点。

图6 稳态时输出电压和输出电流波形Fig.6 Steady-state waveforms of output voltage and current

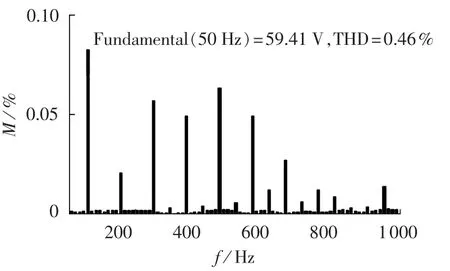
图7 输出电压频谱图Fig.7 Spectrum of output voltage

图8 电感电流波形Fig.8 Waveforms of inductive current

图9 开关管VT1和VT2的驱动信号Fig.9 Driving signals of VT1and VT2

图10和图11是2种控制策略（传统双环控制和双环滑模控制）下系统负载突变时的输出电压和输出电流波形，可以看出：从空载到满载时，2种控制策略的效果都比较好，但传统双环控制在空载时输出电压波形有一定的畸变，满载后幅值有一定的下降；而双环滑模控制则不存在这些问题，其动态响应也要稍快于传统双环控制，且超调量小；从满载到空载时，相较于传统双环控制，双环滑模控制策略在突变的瞬间超调量更小、调整时间更短，输出波形几乎没有变化。这表明采用双环滑模控制策略使系统具有更强的鲁棒性和动态性能。

表1为输出电压和电压调整率随负载变化时的情况，可以看出双Buck逆变器在双环控制下输出电压随负载增大而降低，电压调整率从0.58%到3.27%变化；在双环滑模控制下输出电压随负载增大有升高也有降低，电压调整率从-0.17%到0.66%波动。从表中数据也可以发现双环滑模控制策略比双环控制策略稳压精度更高，电压调整率更小。

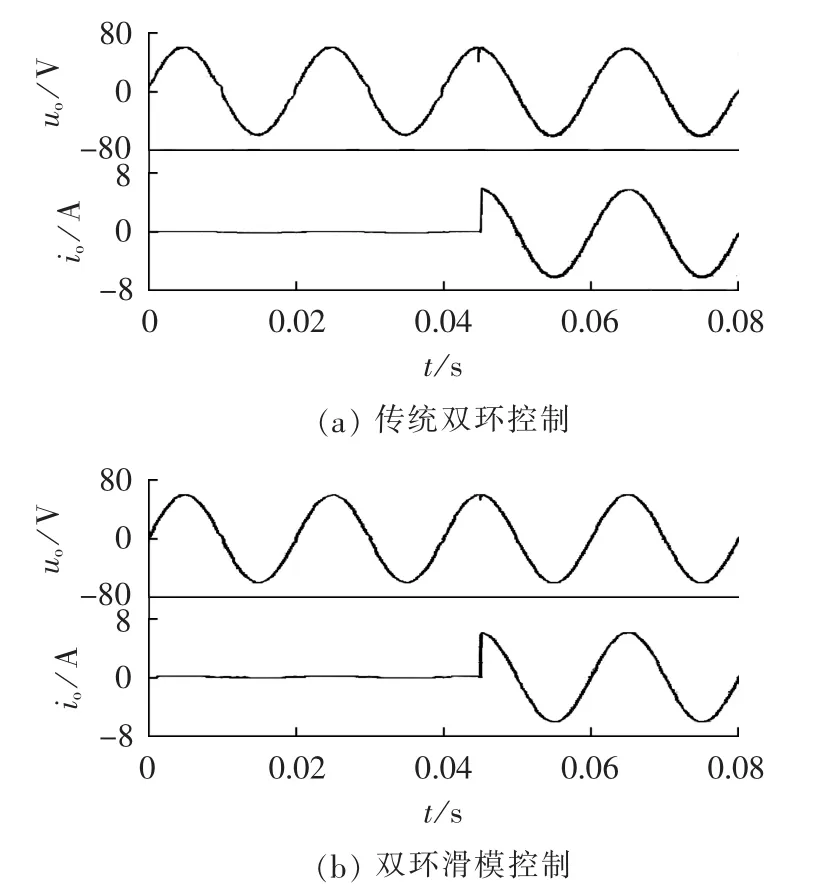
图10 从空载到满载时输出电压和输出电流波形Fig.10 Waveforms of output voltage and current from no-load to full-load

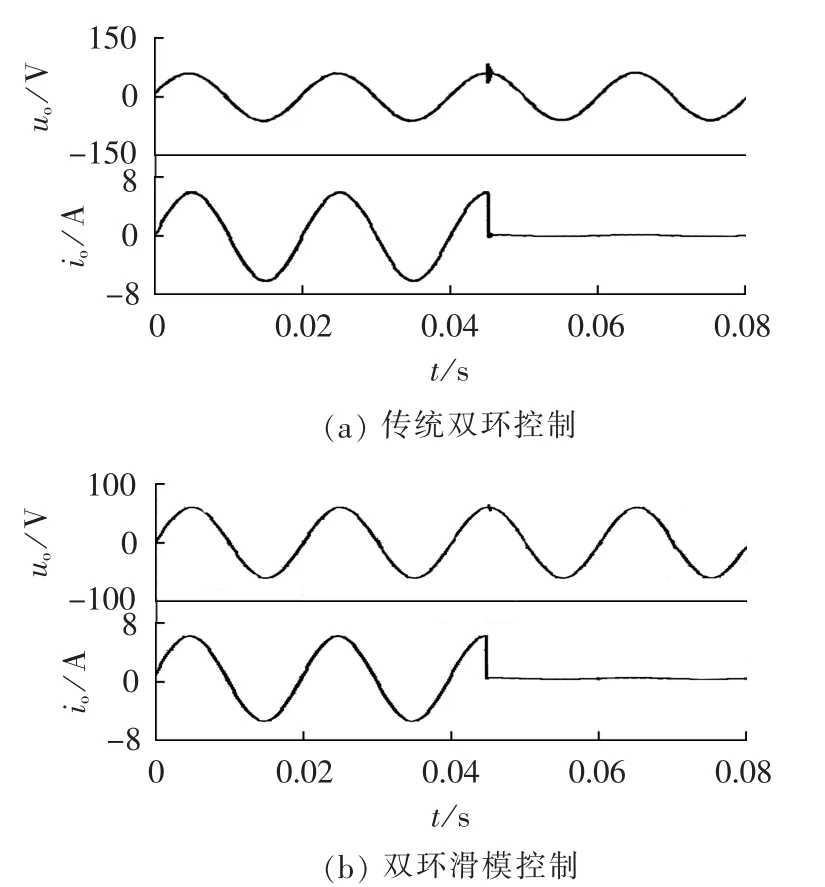
图11 从满载到空载时输出电压和输出电流波形Fig.11 Waveforms of output voltage and current from full-load to no-load

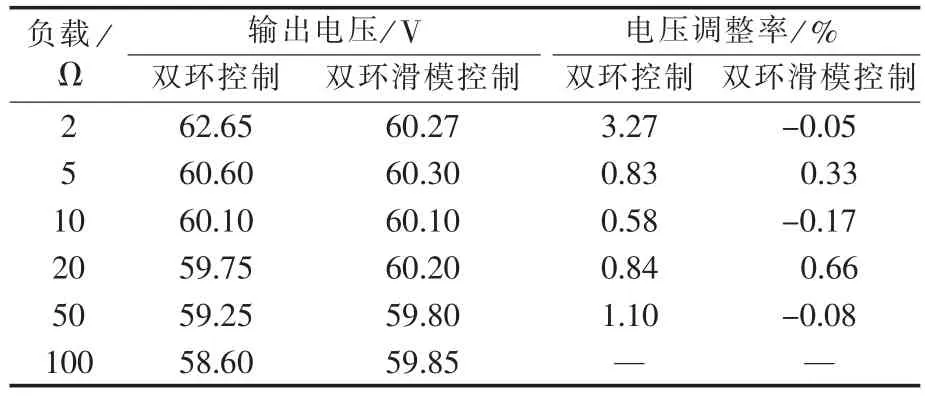
表1 负载变化时输出电压和电压调整率情况Table1 Output voltages and corresponding regulation rates for different load variations

4 实验验证

根据仿真参数设置实验用主电路参数，采样电路分别选择型号为CHB-25 NP电流传感器、CHB-25P电压传感器。因为在滑模控制器设计时，对输出电容电压要进行微分，故间接采样电容电流即可。控制电路和驱动电路分别如图12和图13所示，其中调节施密特触发器LM311的RST1和RST2之比就可调节滞环宽度；由k1=1、k2=k3=RC知，电容电流和电感电压的差分放大器的增益即为RC，以及PI仿真参数可选择控制电路的相关电阻阻值。实验用负载为40 Ω /200 W。

图12 控制电路Fig.12 Control circuit

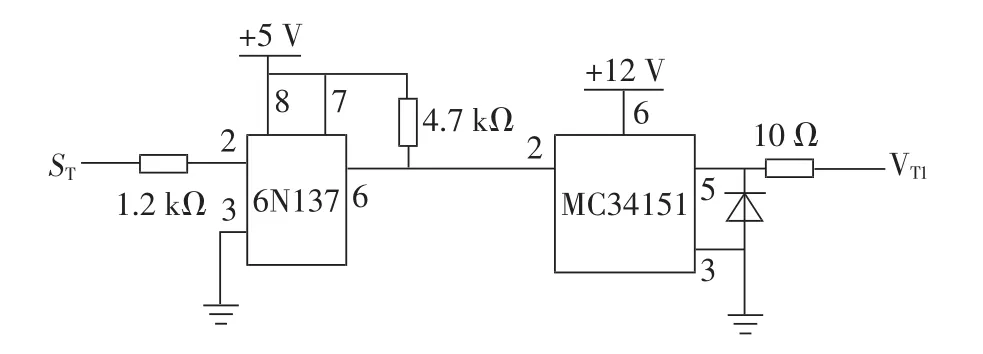
图13 驱动电路Fig.13 Driver circuit

实验结果如图14—16所示。图14为输出电压和电流波形，可以发现输出波形的效果非常好，系统稳态性能佳；图15为开关管驱动信号，可以得到开关管稳态工作时的最高频率达到100 kHz左右。

图16为负载突变实验波形，图16（a）是从满载突然到空载的输出电压和输出电流波形，图16（b）是从空载突然到满载的输出电压和输出电流波形，与仿真结果相比，实验结果也进一步验证了双环滑模控制下的双Buck逆变器具有较强的鲁棒性和动态性能。

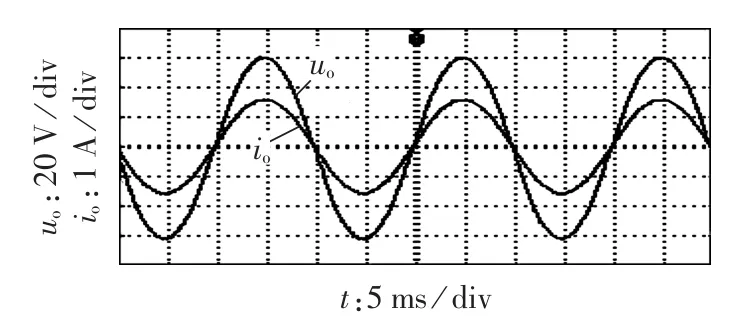
图14 输出电压和电流波形Fig.14 Waveforms of output voltage and current

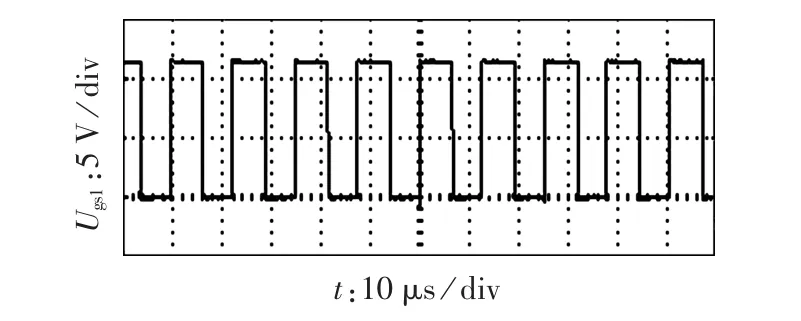
图15 开关管VT1的驱动信号Fig.15 Driving signal of VT1

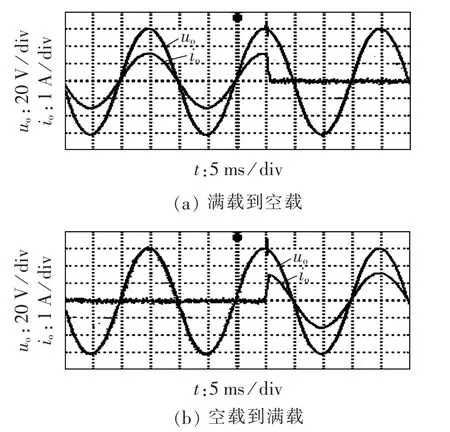
图16 负载突变时输出电压和输出电流波形Fig.16 Waveforms of output voltage and current for sudden load changes

5 结论

本文通过分析双环控制下双Buck逆变器输出电压调整率的影响因素，结合双环控制方法，提出了一种双环滑模控制策略。选取电容电压误差及其微分、电感电流误差为状态变量建立了系统的状态方程，然后对滑模控制器进行了设计。最后进行了仿真分析与实验验证，结果表明采用双环滑模控制的双Buck逆变器稳态精度高、谐波畸变率小、带负载能力强，具有很好的动态和稳态性能。