考虑大停电风险的多阶段电网扩展规划方法

曹一家，曹丽华，李 勇，张宇栋

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.国网四川省电力公司电力科学研究院，四川 成都 610072）

0 引言

近年来，连锁故障大停电事故在世界各地频繁发生[1]，它们与电网结构薄弱、运行压力较大有着密切的关联[2-3]。建设坚强可靠的电网必须要预防与控制大停电事故的发生，应该从电网规划阶段开始降低系统的大停电风险水平。电网扩展规划TEP（Transmission Expansion Planning）是复杂的优化问题，在确保电网满足负荷预测需求和可靠性标准的同时，还要最小化整个规划周期内的投资费IC（Investment Cost）、运行费 OC（Operating Cost）和停电损失费之和[4]。要获得经济可靠的电网扩展规划方案，首先必须获得待选规划方案相应的可靠、充足的停电统计数据。

对实际电网历史停电数据的分析表明，停电规模的概率分布函数具有幂律尾而不是指数尾，这说明停电事件之间存在长期依赖关系[5]。自组织临界SOC（Self-Organized Criticality）理论认为，广延耗散动力系统在各种作用力下，可以自发地朝着临界状态演化；在临界状态下，系统“雪崩”事件具有时空幂律分布[6]。由此可见，不少实际电网具有自组织临界特性。基于自组织临界理论，学者们提出了OPA（ORNLPSerc-Alaska）模型，通过模拟电力系统演化特征获得停电统计数据，最终用来研究电力系统的全局动态特性[7]。然而，OPA模型的电网升级步骤并未体现电网规划方案对电网升级的指导作用。

另一方面，传统电网可靠性分析一般采用确定性方法，如“N-k”校验准则。该方法计算耗时随系统规模和k值的增加呈指数增加，且常导致投资过度。概率性方法则是指利用一定的方法模拟系统运行特征，并通过大量仿真获得一组停电统计数据，然后利用这些数据计算概率性风险指标，用以评估系统的风险水平。常见概率性风险指标包括预期负荷损失ELL（Expected Load Loss）[8]、风险价值 VaR（Valueat-Risk）和条件风险价值CVaR（Conditional Value-at-Risk）[9]等，但这些指标在一定程度上掩盖了极端事件（如连锁故障大停电事件）的影响后果。因此，需要寻找一个不同于期望损失性质的新指标，从一个新的视角来衡量这类事件的风险。

考虑到电网扩展规划行为对系统全局动态特性的影响，本文提出一种适用于多阶段电网扩展规划的OPA（TEP-suited OPA）模型，可为规划方案的风险评估提供更可靠、充足的停电统计数据。为充分计及电网连锁故障对扩展规划的影响，本文又提出一种可衡量大停电风险的幂律尾风险PTR（Power-law Tail Risk）指标，并将其作为规划方案的可靠性评估指标之一。一般而言，在电网规划的寻优过程中，使用概率性方法几乎是不可接受的，因为评估待选方案的计算量巨大，在系统规模较大时该问题尤为突出。鉴于此，本文采用双层优化策略解决该问题[10]。首先，利用改进的多目标粒子群优化 MOPSO（Multi-Objective Particle Swarm Optimization）算法搜索出一组满足基本潮流约束的、高质量的待选规划方案；其后，利用TEP-suited OPA模型获得这些待选规划方案的停电统计数据，并计算待选方案的风险指标；最后，综合考虑可靠性和经济性，对待选方案进行评估。

1 TEP-suited OPA模型

1.1 基本OPA模型

基本OPA模型是为研究电力系统全局动态特性而提出来的，其主要思路如下：随着电力系统发电能力和负荷水平不断上升，支路潮流相应增加，当支路潮流接近或超过支路传输极限时会以一定概率开断，而一条支路的开断又会导致其他支路潮流增加，进而导致其他支路的相继开断，最终形成连锁故障；另一方面，因过载而断开的支路被认为需要进行改造，以增加系统的可靠性。可见，基本OPA模型涵盖了快、慢2个时间尺度。其中，慢动态用于描述负荷增长和传输容量增长2种反作用力；快动态用于描述连锁故障线路跳闸过程，而这种跳闸过程耦合了慢动态中的2种反作用力，使得电网自发地朝着临界状态演化。为了使OPA模型能够更加真实地刻画电网演化特征，本文提出了一种适用于多阶段电网扩展规划的TEP-suited OPA模型。

1.2 TEP-suited OPA模型的慢动态

慢动态用于描述长时间尺度下的电网升级特征。在基本OPA模型中，负荷和发电容量“每天”缓慢、均匀地增长；线路只有发生故障时其容量才会增长。事实上，电力公司根据历史停电数据和投资约束搜寻经济、可靠的电网扩展规划方案，据此有计划、逐步地对电网进行升级。因此，在TEP-suited OPA模型中，仅在每个规划阶段的开始时刻根据规划方案对负荷、发电容量和支路传输容量进行更新。

1.3 TEP-suited OPA模型的快动态

快动态用于描述短时间尺度下的连锁故障过程，不同的系统状态产生不同的停电统计数据。在TEP-suited OPA模型中，由于慢动态取消了基于平均效应的长期演化行为，为了获得充足的停电统计数据，在快动态中利用蒙特卡洛方法对每个规划阶段对应的系统状态进行大量仿真，即一个多阶段电网扩展规划方案的停电统计数据是由每个阶段系统状态对应的停电统计数据组成。此外，尽管连锁故障大停电事件发生的概率小，但其影响严重，为了进一步保证大停电事件数据的充分性，所提出的新模型采用重要性采样技术，以提高小概率事件的采样效率。

为了确保停电统计数据的可靠性，新模型充分考虑了对连锁故障有重要影响的因素。隐性故障是导致相继故障大范围传播的重要原因之一[11]，因此新模型引入了隐性故障概率参数。考虑到历史停电数据对电网长期演化的影响，即相邻规划阶段之间的耦合关系，新模型在多阶段规划过程中对初始故障概率参数进行了调整。

1.3.1 隐性故障概率

考虑到在实际电网中线路故障比较常见，本文在快动态中引入了基于线路保护的隐性故障，其传播机理如下：如果一条线路跳闸，则与该线路相连的所有线路保护都有可能发生误跳闸行为，这些线路被称为暴露线路，其表征了可能的隐性故障位置。每条暴露线路的误跳闸概率，即隐性故障概率phf，是该保护装置测量阻抗的函数，其计算公式如下：

其中，z为由暴露支路远离故障端一侧的保护装置测量到的阻抗值；z3为距离保护第Ⅲ段的整定阻抗，定义为暴露支路本身阻抗值的250%。当测量阻抗小于3倍Ⅲ段整定值时，暴露支路的隐性故障概率为常数p0，否则隐性故障概率随测量阻抗值的增长呈指数下降。

1.3.2 初始故障概率

连锁故障发生之前，每条支路都有一个初始故障概率pif。在基本OPA模型中，该概率用于描述电网外部环境对支路故障的影响，例如闪电、冻雨、飓风、地震等自然灾害。为了反映历史停电数据对电网后续演化的影响，本文在pif中增加了支路的历史停电概率参数pfr。这是因为，曾经多次故障的支路在电网规划过程中被视为电网的脆弱环节，等效于将该支路的停电风险设置为较大值。为了体现电网规划的此行为特征，本文将支路的初始故障概率与其历史停电概率相关联，此时规划方案的风险水平不仅与现有系统状态有关，还与历史运行情况有关，综合量化了那些作用机理不明、作用相互耦合、人为因素等难以量化衡量的风险因素的影响。支路l的初始故障概率的计算公式如下：

其中，pec为常数，代表电力系统外部环境的影响；pfr，l为支路l的历史停电概率，利用快动态过程获得的上一个规划阶段的停电数据计算得到。

1.3.3 重要性采样技术

连锁故障大停电是小概率事件，要获得足够多的有效数据，直接采用蒙特卡洛方法需要较长的时间。重要性采样技术[12]通过提高采样概率，以增加小概率事件发生的次数，可有效减少无效仿真次数，大幅提高了蒙特卡洛方法的采样效率。令pj为第j条暴露支路的实际隐性故障概率，pmax为所有pj中的最大值，uj为[0，1]之间的均匀分布的随机数，则第j条暴露支路在仿真中的采样概率为：

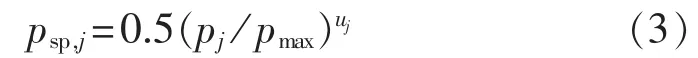
为更清晰地了解所提TEP-suited OPA模型的工作原理，将其与基本OPA模型进行比较，见表1。

2 幂律尾风险PTR指标

在概率统计学中，互补累积分布函数CCDF（Complementary Cumulative Distribution Function），亦简称为尾分布或超出数，用于研究一个随机变量超出一定值的概率分布。因此，本文提出了一种幂律尾风险PTR（Power-law Tail Risk）指标，并将其定义为停电事件规模的CCDF曲线幂指数绝对值的倒数，用于衡量系统大停电风险，其公式如下：

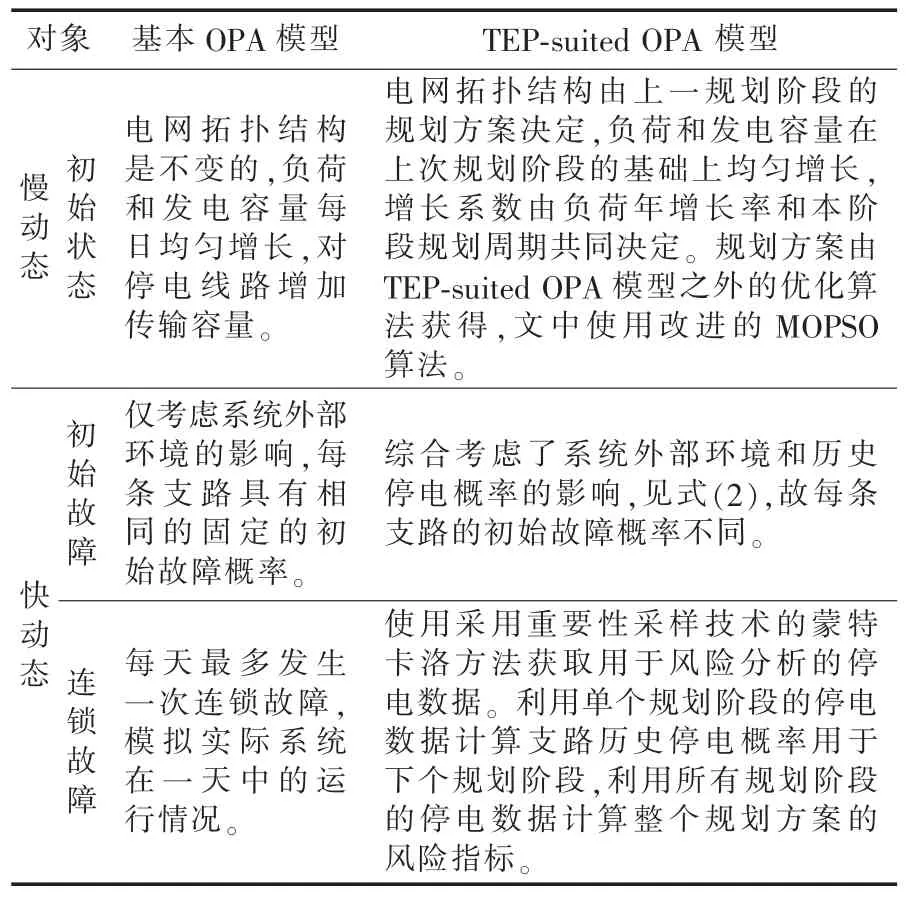
表1 基本OPA模型和TEP-suited OPA模型的对比Tab.1 Comparison between classical and TEP-suited OPA models

其中，随机变量 X 表示停电规模；P（X＞x）为 X＞x的概率值。

由定义可知，幂指数绝对值α越小，则PTR越大，PTR描述大停电事件发生概率的变化趋势，而不是所有停电事件的预期负荷损失，是一个局部风险指标。文献[13]提出了一种估计分布函数尾部特征的简单方法。该方法无需对整个分布函数进行拟合，只需拟合需要评估的尾部数据的表达式，这大幅降低了拟合的复杂程度。

3 多阶段电网扩展规划方法

3.1 目标函数

电网规划目标基本可分为互相冲突的经济性和可靠性两大类，分别用IC和风险指标来描述。

3.1.1 IC

通常，IC 包括建设费 CC（Construction Cost）和OC，是电网扩展规划问题最基本的目标函数。CC是指新建支路的建设成本总和，OC则由生产费、线损费和缺电损失费共同组成[14-15]。多阶段（动态）电网规划，其规划周期被划分成多个阶段。假设年贴现率为e，为方便公式书写定义 1-I=（1+e）-1，其中 I不对应实际物理意义；参考年为t0，初始年为t1，规划周期总共为tS+1-t1年，被分成了S个阶段，那么一个多阶段电网扩展规划方案的CC和OC折合到参考年的现值为：

其中，c（x）和 d（x）分别为 CC 和 OC 折算到参考年的现值；s为规划阶段的序号，S为规划阶段的总数；cs（x）和 ds（x）分别为第 s个规划阶段的 CC 和 OC（非现值）；δcc，s和 δoc，s分别为第 s 个规划阶段的 CC 和OC的折现系数。

本文试图通过证明以下2个观点来验证所提出的考虑大停电风险的多阶段电网扩展规划方法是切实有效的，即TEP-suited OPA模型能够提供更加准确的停电统计数据；PTR能够有效地衡量大停电事件的风险水平（即PTR相较其他风险指标具有相似性和独特性）。首先，目标函数（IC）的精确程度不会影响优化算法的性能，也不会影响PTR和其他风险指标之间的相对关系；其次，TEP-suited OPA模型的准确性主要依靠于相邻规划阶段之间的耦合关系，同样与IC的计算精度没有关系。因此，在不影响研究目的前提下，为了降低整个规划流程的计算复杂度和计算量，OC不考虑生产费和线损费。此时，CC和OC（非现值）可写为：

其中，cl、bl和 xl，s分别表示在支路 l新增一回线路每km的投资费用、支路l的长度和支路l在第s阶段新增线路的回数；βk为节点k单位负荷损失费用；r为节点负荷损失，rk，s为节点k在第s阶段的负荷损失量，由网络安全标准和最小切负荷方法[7，10]共同决定。为了减少不必要的计算量，在MOPSO算法中用“N-0”校验准则（即完整电网是否满足基本的潮流约束）下的最小切负荷量来衡量方案的风险水平。

3.1.2 风险指标

通常的规划方法以确定性风险指标如“N-k”校验准则为基础。若要进一步提高规划方案的可靠性，可增加其他非确定性风险指标。相较于确定性风险指标，概率性风险指标计算量更大。因此，本文采用双层优化策略，将概率性风险指标放到迭代程序（优化算法）之外处理，以降低整个规划流程的计算量。本文的可靠性目标函数仅指概率性风险指标，确定性风险指标已经暗含到投资费用中。为了验证PTR的有效性，下面分析PTR与其他概率性风险指标（ELL、VaR和CVaR）之间的相对关系。

令 U=｛B1，B2，…，BM｝为所有停电故障路径的集合，Ci为故障路径Bi对应的负荷损失，并假设Bi包括Ni条暴露支路，其中ni条导致了保护装置的隐性故障，那么该停电故障路径Bi的发生总概率为：

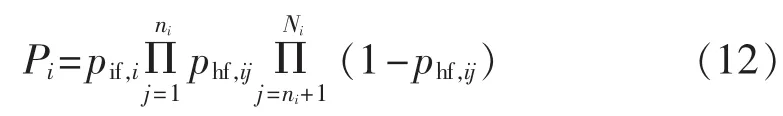
其中，pif，i为 Bi中初始故障支路的初始故障概率；phf，ij为Bi中第j条暴露支路的隐性故障概率。那么，单次故障路径的预期负荷损失为：

值得注意的是，预期负荷损失ELL与概率统计学中的期望值E[X]具有相同的表达形式，但是在ELL中Pi表示事件i的发生概率，Pi的累加和不等于1；而在E[X]中Pi表示规模等于xi的事件的出现频率，所有Pi相加等于1。

假设δ为置信水平，p（x）是连续随机变量X的概率密度函数 PDF（Probability Density Function），则VaR和CVaR定义如下：

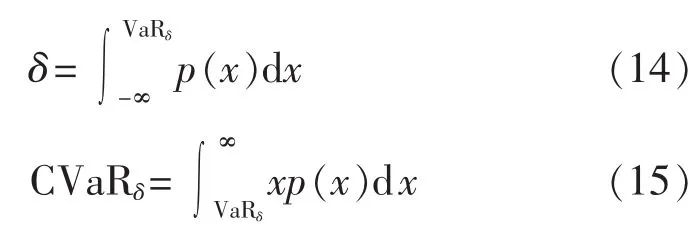
其中，停电规模的概率密度函数p（x）可利用停电统计数据进行估算。首先，将停电规模空间（从停电规模最小值到最大值）分为有限个小间隔；然后，统计落入每个间隔的停电事件的次数，该数除以停电事件总数即为对应间隔的概率值。

由式（4）、（5）描述的 PTR 指标及式（13）—（15）可知，ELL评估单次停电事件的平均影响，VaR表示在一定置信水平下停电事件的损失上限，ELL和VaR分别描述所有停电事件和大多数停电事件的预期负荷损失，两者均为综合性风险指标。CVaR是停电损失超出VaR值的期望值，PTR测量大停电事件的互补累积概率函数（CCPF）的变化趋势，CVaR和PTR分别从不同的角度评估极端停电事件的风险水平，两者都是局部性风险指标。

3.2 多阶段电网扩展规划的表征

电网扩展规划问题是一个大规模、混合整数、非线性且非凸问题，可用如下标准优化模型描述：

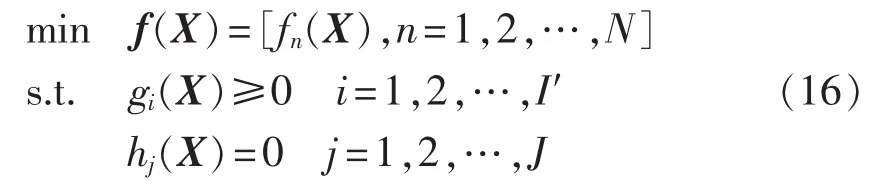
其中，X 是解向量；fn（X）、gi（X）和 hj（X）分别为第 n个目标函数、第i个不等式约束、第j个等式约束。不等式约束主要包括IC约束、潮流约束等，等式约束主要指功率平衡约束。

采用实数编码的多阶段电网规划问题的解可描述为：

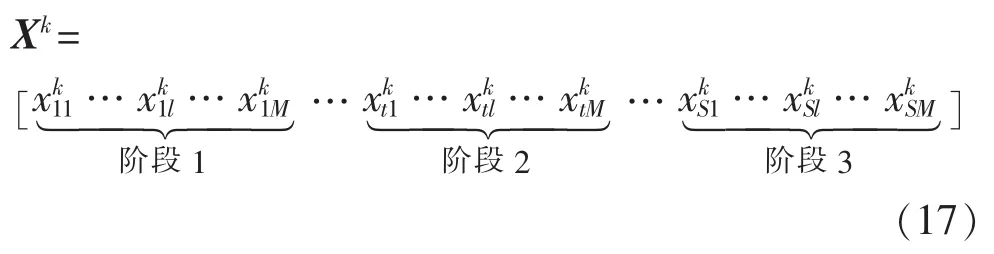
其中，Xk表示第k个待选规划方案；S为规划阶段的总数；M为待选支路的总数；xktl表示方案k在第t个规划阶段在待选支路l上新增线路的数目。静态规划时，Xk=[xk1…xkl…xkM]。

大多数的约束限制源于“N-0”校验准则，如支路传输容量约束、发电机发电容量约束等。此外，在任意规划阶段待选支路上的线路总回数都不能超过其允许上限，该约束可描述为：

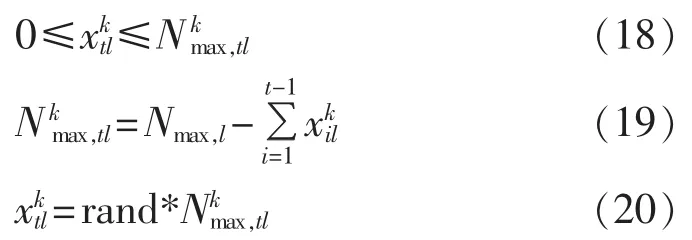
其中，Nmax，l为整个规划周期中待选支路l上可增加线路的上限；Nkmax，tl为方案k在规划阶段t时，待选支路l上最多可增加线路的上限，其值随方案和规划阶段的不同而不同；随机函数rand产生[0，1]之间均匀分布的随机数。为确保初始解在搜索空间范围内，可利用式（20）产生初始解。

3.3 方法流程图

本文采用改进的MOPSO算法求解电网扩展规划问题。该算法采用含约束条件的非受控解排序算子[16]、全局最优引导者概率选择算子[17]提高解的多样性，用指数分布边界处理算子[17-18]修正不可行解。

考虑大停电风险的多阶段电网扩展规划方法的流程如图1所示。为降低计算耗时，利用双层优化策略将规划流程分为2个阶段。首先以投资费用为目标函数，应用MOPSO算法搜索满足一定经济性约束和电网正常运行潮流约束的待选方案；然后，计算待选方案的非确定性风险指标；进一步地，基于目标函数筛选出帕累托最优解，为电网规划人员的决策制定提供精简有效的信息。

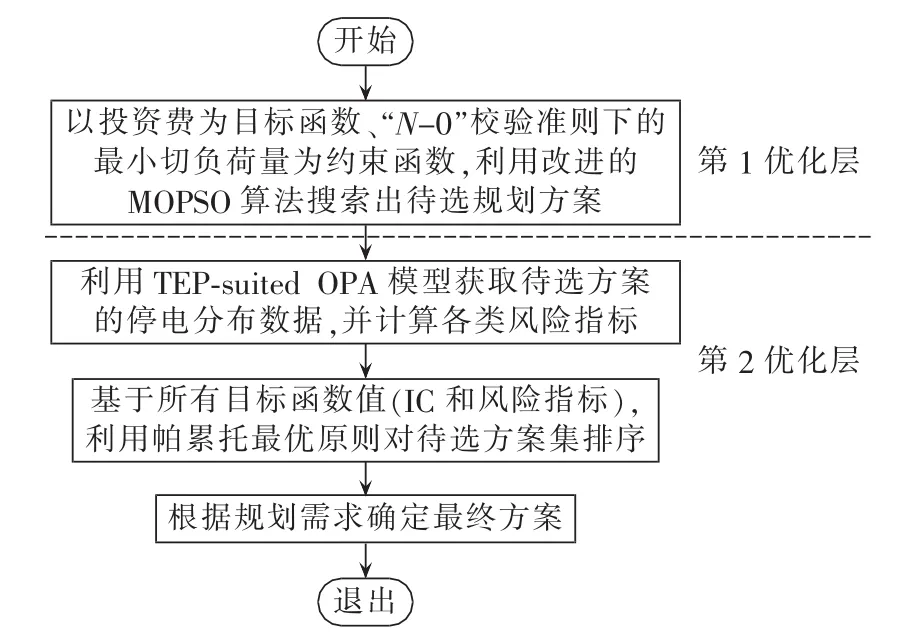
图1 所提方法流程图Fig.1 Flowchart of proposed method

4 算例分析

4.1 Garver系统

Garver系统在扩展之前的结构如图2所示。该系统有6个节点，6条传输线路，装机容量为1110MW，最大负荷为 760 MW[15，19]。 假设扩展周期 6 a，分为 3个规划阶段，且参考年亦为初始年；负荷和发电容量年增长率为5%，则到规划周期的最后时刻装机容量和负荷总量分别达到1110×1.056=1487.5（MW）和760×1.056=1018.5（MW）；任意两节点之间最多可连4回线路，单回线路的CC为1.00×106/km；贴现率e=10%。

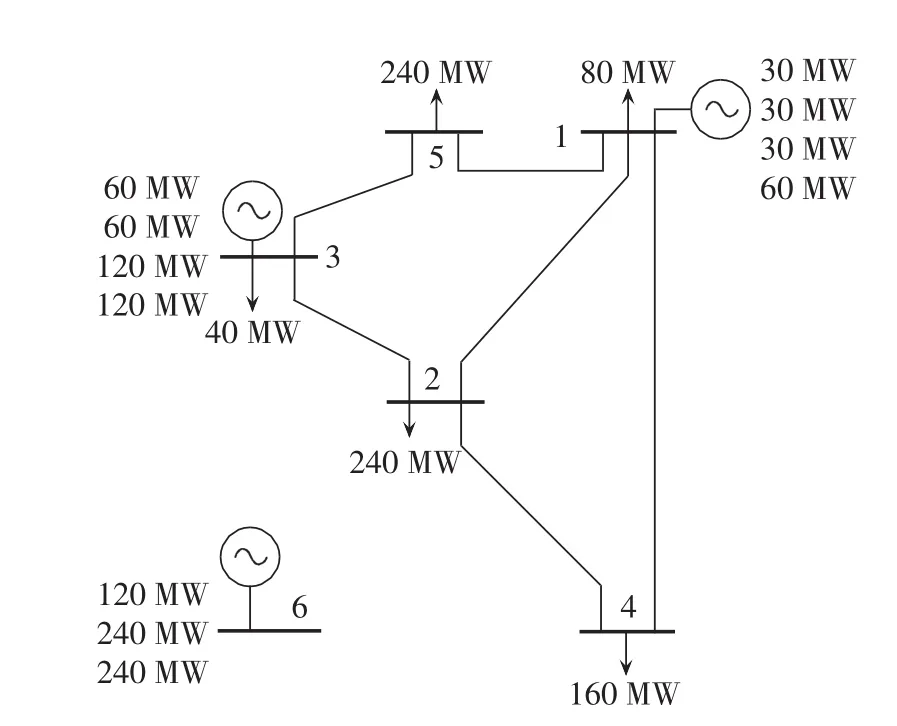
图2 原始Garver系统Fig.2 Initial Garver system

4.2 仿真结果分析

4.2.1 相邻规划阶段耦合关系的影响

选取投资费用最少的20个规划方案为待选方案。图3（a）、（b）分别给出了相邻阶段有耦合关系和无耦合关系时，待选方案的风险指标ELL和PTR。图3中，方案编号按CC从小到大排序。

由图3可知，有耦合关系的ELL普遍小于无耦合关系的 ELL，但与此同时，方案｛4，9 —13，17｝的PTR在有耦合关系时略高于无耦合关系。这说明在电网长期演化过程中，耦合关系降低了系统的平均停电风险，但增加了系统的大停电风险。这种耦合关系很好地解释了实际停电事件之间的长期依赖关系。由此可见，TEP-suited OPA模型能为决策制定者提供更加符合实际的停电统计数据。

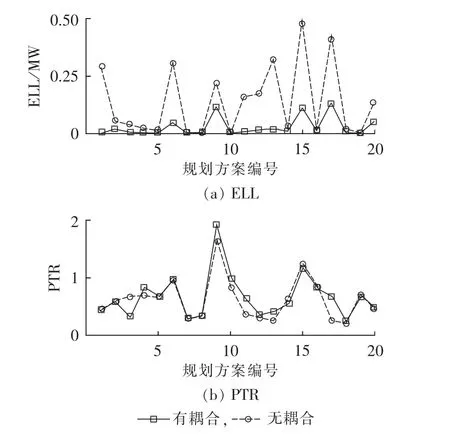
图3 耦合关系对停电风险指标的影响Fig.3 Impact of coupling relation on risk indices

4.2.2 PTR的有效性

表2给出了相邻规划阶段存在耦合关系时待选方案的目标函数值，包括IC、ELL、VaR、CVaR和PTR（由于IC值较大，记IC′为IC与其上限值的比率）。

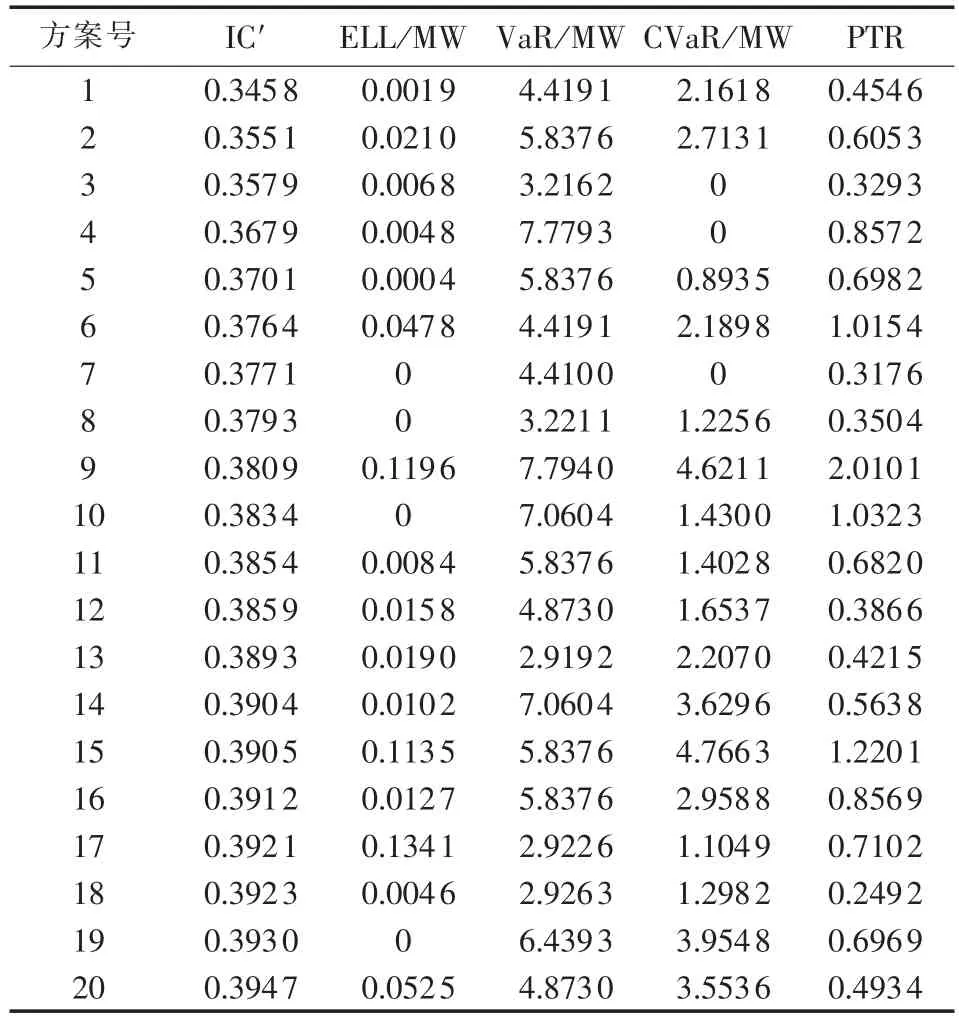
表2 待选方案的目标函数值Tab.2 Objectives of candidate plans

为进一步分析PTR的有效性，图4对PTR和其他风险指标进行了对比。由图可知，随着IC增加，各类风险指标呈波动变化，表明电网规划方案的停电风险并不总是随着IC的增加而降低。因此，利用优化算法寻找较优的规划方案有意义且可行。

从图4（a）可知，随着IC增加，规划方案的局部风险指标PTR和CVaR的变化趋势大致相同，但并不完全一致，少量方案如方案｛4，18｝的PTR变化趋势与CVaR变化趋势相反，说明PTR和同类风险指标相比具有相似性。从图4（b）和（c）可见，PTR和不同类型风险指标的变化趋势差别较大，VaR和ELL等综合型风险指标与局部型风险指标PTR可互相补充。上述结果验证了PTR的合理性和有效性。

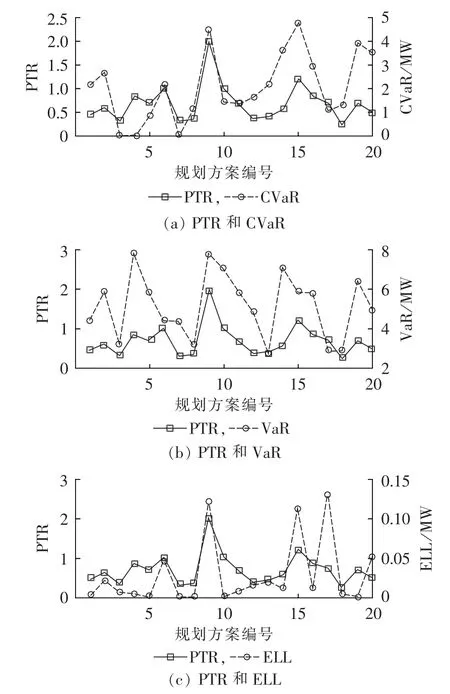
图4 不同风险指标的比较Fig.4 Comparison of risk indices

4.2.3 最终方案的确定

假设在电网扩展规划中考虑经济性、常规停电风险和大停电风险，即目标函数包括IC、ELL和PTR。首先，利用帕累托最优原则[16]对待选方案（解）排序，结果见表3。决策制定者按规划需求从一级帕累托前沿中选出最终方案。由表3可知，一级帕累托前沿包括方案｛1，3，5，7，10，18，19｝，拥挤距离为无穷（Inf）的解，说明在同级帕累托前沿中该解至少有一个目标函数值位于边界，如方案1的IC最小，方案19的IC最大，方案18的PTR最小。综合考虑所有因素，假设方案3被选定为最终方案，令nx-y表示在节点x和y之间新增线路的数目，则方案3的各阶段具体扩展步骤如下：

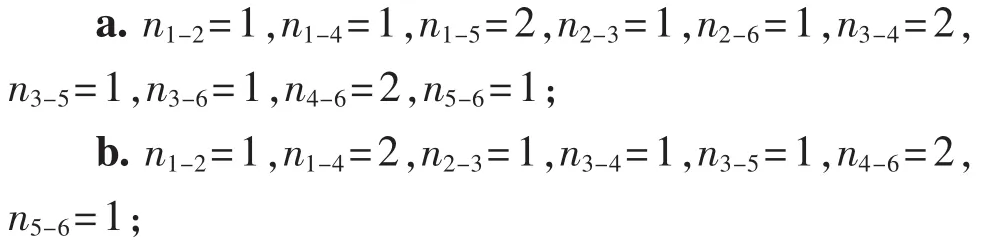
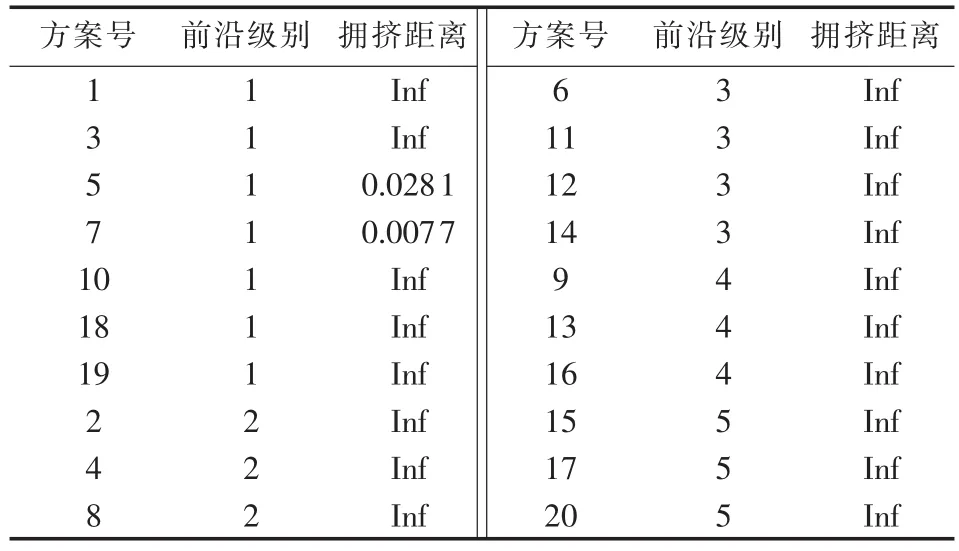
表3 待选方案的帕累托前沿Tab.3 Pareto front of candidate plans

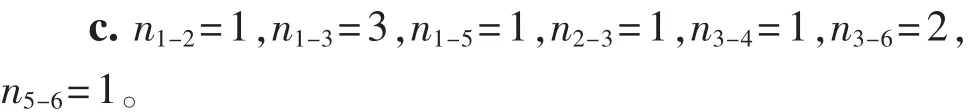
5 结论

本文提出了一种考虑大停电风险的多阶段电网扩展规划方法，定义了用于衡量系统大停电风险的PTR指标，建立了用于获得规划方案停电统计数据的TEP-suited OPA模型，并采用改进的MOPSO算法和双层优化策略来实现电网规划的寻优过程。基于Garver 6节点系统对所提规划方法的有效性进行了测试。结果表明，相邻规划阶段之间的耦合关系降低了系统的平均停电风险，但增加了大停电风险，这合理解释了系统自组织临界行为特征，证明了TEP-suited OPA模型能提供更加真实的停电统计数据。本文提出的PTR能有效衡量大停电风险，结合其他综合型风险指标，可为规划决策人员提供更全面的风险评估信息。此外，结果还表明，电网规划方案的停电风险并不总是随投资费用的增加而降低，可利用优化算法寻找经济可靠的规划方案，前提是优化算法搜索到的解具有足够的多样性。