考虑风电并网的发电充裕度评估方法的比较
陈 凡,卫志农,黄 正,孙国强,刘海涛
(1.南京工程学院 电力工程学院,江苏 南京 211167;2.河海大学 能源与电气工程学院,江苏 南京 210098)
0 引言
化石能源价格的上涨、公众对环境问题的日益关注使得风力发电在世界各国范围内受到了广泛的重视[1-2]。然而风力发电具有随机性和间歇性的特点,风电机组输出功率波动大、难以控制,这使得风力发电对电力系统可靠性有较大影响;当系统中风电的比例增加时,风力发电对系统可靠性的影响将更加显著[2]。
对风电并网后的电力系统可靠性进行评估的方法可分为解析法和蒙特卡洛模拟法两大类[2-4],根据抽样原理的不同,蒙特卡洛方法可以分为状态抽样法和状态持续时间抽样法2种。现有文献采用不同的可靠性评估方法研究了风电并网后的电力系统可靠性状况:文献[3,5]通过建立风电场的解析模型,采用解析方法进行充裕度评估;文献[1,4,6-7]通过建立多降额状态的风电场模型,采用状态抽样的模拟方法开展研究;文献[8-10]则通过采用状态持续时间抽样法对风电场输出功率状态的持续时间模拟来进行评估。但是哪种方法更适合进行风电并网发电系统的充裕度评估,目前还没有文献对这3种评估方法进行比较研究。
本文对3种发电充裕度评估方法进行了简要概述,提出了一种考虑风电机组随机停运的建立风电场解析模型的方法,并将其与状态持续时间法中计及风电机组随机停运时的风电场建模方法进行了比较分析;最后以RBTS和IEEE RTS79测试系统[11-12]为例,分别采用3种方法进行发电充裕度评估,并对3种方法所得的算例结果进行了比较分析,指出状态持续时间抽样法更适合进行风电并网后的系统可靠性评估。本文的研究结果为选取合适的评估方法进行其他间歇性能源接入后的系统可靠性计算提供了参考依据。
1 发电系统充裕度评估方法简述
1.1 解析法
解析法根据电力系统元件的随机参数,建立系统的可靠性数学模型,通过数值计算方法获得系统的各项指标。解析法基于马尔可夫模型,准确度较高,但解析法的计算量随系统规模的增大呈指数增长,因此解析法一般只适合于网络规模较小而网络结构较强的系统[13]。采用解析法进行发电系统可靠性计算的关键在于建立发电系统和时序负荷的可靠性模型,通常采用递推算法或分级的方法建立发电容量概率模型,采用K-均值聚类算法将电力系统的年时序负荷聚类成多级负荷模型[14]。在获得发电容量概率模型和多级负荷概率模型之后,即可利用卷积公式计算发电充裕度指标。通常采用电力不足时间期望 LOLE(Loss Of Load Expectation)、电量不足期望 LOEE(Loss Of Energy Expectation)指标来表示发电系统的充裕度,这2个指标计算的卷积公式如下[13]:

其中,Li是第i级负荷水平;Pi是第i级负荷水平概率;NL是负荷水平分级数;Gj是第j级发电容量;Pj是第j级发电容量的概率;NG是发电容量分级数;T是负荷持续曲线时间总长度。
1.2 状态抽样法
状态抽样法的依据是:一个系统状态是所有元件状态的组合,且每一个元件状态可由对元件出现在该状态的概率进行抽样来确定。每台发电机的概率特性可用一个处于[0,1]之间的均匀分布来描述,通常采用两状态模型来表示发电机组状态(即故障和运行2种状态),按照发电机的状态确定每台机组的可用容量,将各台发电机可用容量求和即可获得系统总的发电容量。对应于某一给定负荷水平时,第k次抽样的电力不足为:
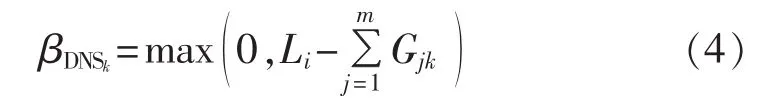
其中,Gjk是第j台发电机在第k次抽样中的可用容量;m是发电机台数。
将发电系统容量状态抽样结果和多级负荷模型中的每一级负荷水平结合,根据式(5)、(6)进行统计计算即可得出电力不足时间期望、电量不足期望等指标[13]:
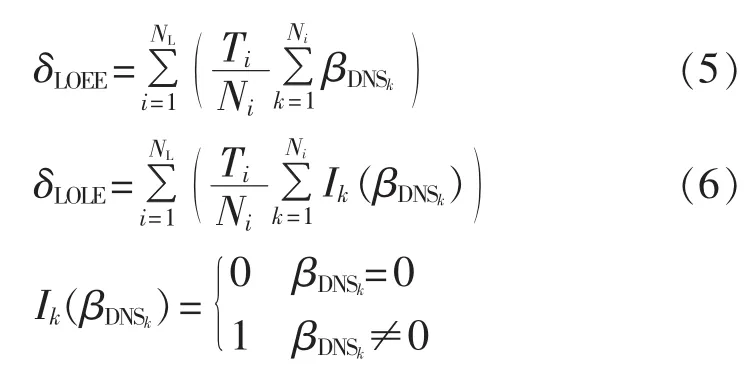
其中,Ti是第i级负荷水平的时间长度;Ni是第i级负荷水平的抽样数;Ik是指示变量。
1.3 状态持续时间抽样法
状态持续时间抽样法通过模拟系统运行的随机过程来实现可靠性指标的统计计算。发电机组采用两状态模型表示,即认为发电机组的故障率与修复率都为常数,正常运行持续时间与故障修复时间均服从指数分布,则发电机组的正常运行持续时间 τ1和修复时间τ2为[15]:

其中,γ1、γ2是[0,1]之间的均匀分布随机数;TMTTF是平均持续工作时间;TMTTR是平均修复时间。
状态持续时间抽样法采用时序负荷模型,将状态持续时间抽样法生成的发电容量的时序曲线和负荷时序曲线重叠之后可以得到系统的发电充裕度时序曲线,系统的发电充裕度指标计算公式如下[13]:

其中,N是仿真总年数;ti是第i年的电力不足持续时间(h);Wi是第 i年的电量不足(MW·h)。
2 3种评估方法中的风电场建模
2.1 解析法和状态抽样法中的风电场建模
采用解析法或状态抽样法进行风电场可靠性评估时通常忽略风速时变性对风机出力的影响,将风机看作多状态单元或者有限出力单元[3,16],并使用容量停运概率表作为其容量概率模型。对于其中风力发电机等效状态的数目,需要通过对计算精度和计算工作量进行综合权衡之后作出合适的选择,文献[5]指出5个状态的风电模型适用于采用解析法或者状态抽样法进行充裕度评估。文献[17]则进一步指出风速状态数目至少是4阶时才能保证较好的精度。
2.1.1 风速时间序列的产生
根据历史风速数据的统计资料,可以采用预测方法或者模拟方法来获取未来的风速时序序列。常用的风速预测方法有时间序列法、支持向量机法、遗传算法等,这些方法只需要风电场的风速时间序列即可建立模型进行预测。在模拟方法中,根据风速分布函数采用概率分布的逆运算即可模拟出符合预测参数的风速序列[15],通常根据威布尔分布参数模型来模拟未来风速时间序列。根据所获取风能资源的统计资料的不同,可以采用不同的方法来估计威布尔分布的尺度参数和形状参数,主要方法有平均风速和标准偏差法、最小二乘法、平均风速和最大风速估计法、极大似然估计法等[18]。
在威布尔分布参数模型中,假设风速是服从威布尔分布的随机变量,其概率密度函数表达式由式(11)给出[19]:

其中,c是尺度参数,反映了平均风速,当精度要求不高时参数c可直接取风速平均值;k是形状参数,反映了分布的偏斜度,取值为1.8~2.3,一般取k=2。
相应的等值累积概率函数表达式为:

根据反函数变换法,由式(12)概率分布的逆运算得到每小时的风速随机抽样值:

其中,x是[0,1]区间上的均匀分布随机数。
根据国内某风电场历史实测数据,威布尔分布参数取值分别为c=8.03、k=2.02时,模拟得出的典型的年风速时序图如图1所示。
2.1.2 风电机组功率特性曲线
典型的风电机组功率特性曲线如图2所示。图2中AB段曲线近似为直线,可得式(14)。

图1 某地区典型的年风速时序图Fig.1 Chronological diagram of typical wind speed of a region for a year

图2 典型的风电机组功率特性曲线Fig.2 Typical power curve of wind turbine

其中,vi是ti时刻风电机组轮毂高度处的风速;vci、vco、vN分别是切入、切出、额定风速;PN是额定输出功率;WGi是ti时刻风电机组的输出功率。
2.1.3 考虑风电机组随机停运的风电场概率模型
假设风电场由Nt台相同类型的风电机组组成,则多降额状态的风电场概率模型可通过以下步骤形成。
a.将风电场的出力划分为{A1,A2,…,AN}N 个状态。
b.根据时序风速数据和式(14)计算单台风机输出功率时序值WGi。
c.利用式(15)计算风电场有j台风机发生故障的概率:

其中,q是风电机组的强迫停运率FOR(Forced Outage Rate);j=0,1,…,Nt;)表示二项分布。
d.计算ti时刻风电场有j台风机发生故障时的风电场出力:

e.将步骤d中的风电场出力WFj划归到风电场某一状态。当WFj划归到状态Ak时,指示变量Ikj=1;否则Ikj=0。
f.统计风电场出力为状态Ak的概率:

其中,TW是整个风速数据观测时长。
本文分别以15台和200台Vestas公司生产的V80-2 MW型号(风机的切入风速、额定风速、切出风速分别为4、15、25 m/s)的风机构成的风电场为例,将风电场的输出功率平均划分为6个状态。根据图1所示的时序风速数据和式(14)给出的风电机组特性曲线,利用式(15)—(17)得出 30 MW 和 400 MW风电场的概率模型分别如表1和表2所示,表中百分数表示风电机组强迫停运率,后同。

表1 30 MW风电场的容量停运概率Tab.1 Capacity outage probability of 30 MW wind farm
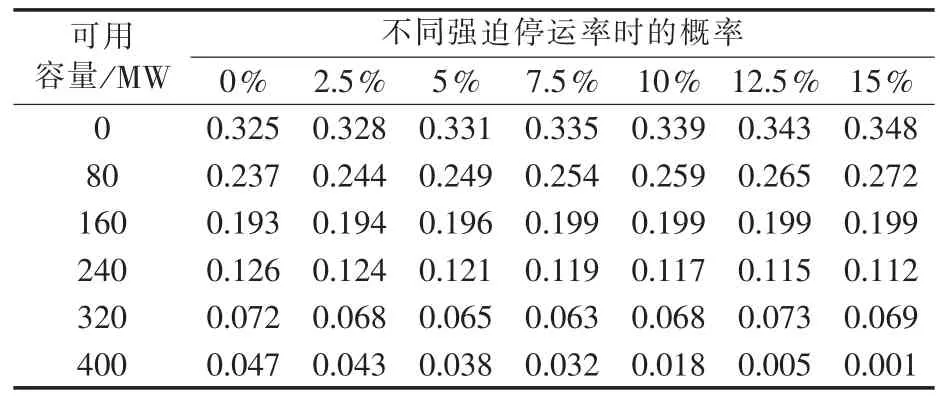
表2 400 MW风电场的容量停运概率Tab.2 Capacity outage probability of 400 MW wind farm
2.2 状态持续时间抽样法中的风电场建模
状态持续时间抽样法采用虚拟的风电场时序曲线作为风电场概率模型,风电机组仍以两状态模型来表示。假设风电机组正常运行持续时间与故障修复时间均服从指数分布,则类似地利用式(7)和(8)即可获取时序的风电场模型。
由上述过程可看到,采用解析法和状态抽样法进行风电并网后的发电充裕度评估时,风电场概率模型的建立过程复杂,风电机组强迫停运率的计入将会进一步增加建模的复杂性;而采用状态持续时间抽样法时风电场的随机停运模拟与传统发电机组组成的发电系统随机运行模拟步骤完全相同,风电机组强迫停运率的计入不会增加建模的复杂性。同时解析法和状态抽样法采用聚类方法将风电场出力聚类为几个状态,存在状态数目难以选择的问题,等效状态数目过多会增加方法的计算工作量,等效状态数目过少又会导致计算精度变差、收敛速度慢。
3 算例分析
3.1 3种评估方法的计算结果比较
本文采用上述3种发电充裕度评估算法分别对RBTS[11](年最大峰荷为 185MW)和 IEEE RTS79 系统[12](年最大峰荷为2850 MW),以及接入30 MW风电场的RBTS系统和400 MW风电场的RTS79系统进行了发电充裕度计算。其中对于解析法和状态抽样法,负荷模型采用K-均值聚类方法[14]将IEEE RTS79系统年时序负荷聚类成20级的多级负荷模型。利用MATLAB 2011b编制程序得出了发电系统的电力不足时间期望δLOLE、电量不足期望δLOEE。蒙特卡洛方法是一个波动收敛的过程,评估结果存在不确定性,因此本文在使用蒙特卡洛法计算充裕度指标时选择以可靠性指标的方差系数作为收敛条件。考虑到与电力不足时间期望的方差系数相比,电量不足期望的方差系数收敛速度更低,因此本文选择以电量不足期望指标的方差系数小于5%作为收敛条件。仿真运行的计算机参数为:IntelR CoreTMi5-3427U CPU@1.80 GHz,4.00 GB内存。仿真结果如表3和表4所示,表中接入风电场后的风电机组强迫停运率为0。
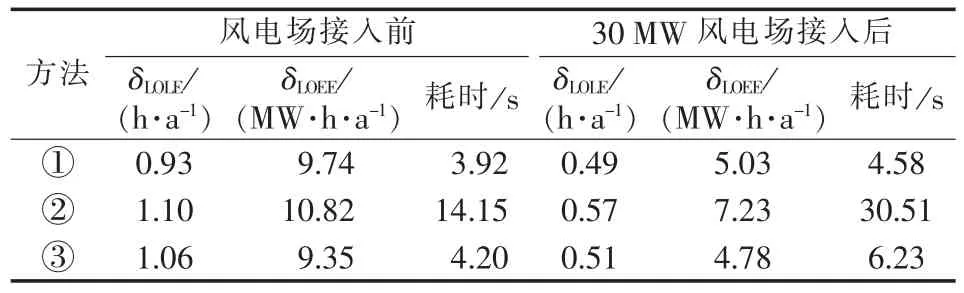
表3 RBTS充裕度计算结果Tab.3 Calculated adequacy of RBTS

表4 RTS79充裕度计算结果Tab.4 Calculated adequacy of RTS79
比较表3和表4中的数据可以得出以下结论。
a.解析法、状态抽样法和状态持续时间法得出的δLOLE、δLOEE计算结果接近,这验证了3种方法和程序编制的正确性;风电场接入之后,系统可靠性指标δLOLE、δLOEE均减小,验证了风电的接入可以改善系统的充裕度指标。
b.对于原RBTS,解析法的计算时间在3种方法中最少,这是因为RBTS的系统规模小,需要枚举的系统状态数目较少,因此解析法评估速度快;风电接入RBTS之后,解析法的计算时间增加很少(仅0.66 s),这是因为本文将风电场等值成6个状态的元件,而原RBTS元件数目、系统状态数目较少,因此加入一个6个状态的等值元件并不会显著增加需要枚举的系统状态数。风电接入RTS79系统之后,解析法计算时间大幅增加,这是因为RTS79系统元件数目、系统状态数目较多,增加一个6个状态的风电场元件,会导致需要枚举的系统状态数大幅增加,倘若风电场等值状态数目增多时,解析法计算时间更会急剧增长。由此可见,解析法仅适用于系统状态数目少、规模较小的发电系统充裕度评估,而实际电力系统一般规模较大,解析法不便用于风电并网电力系统充裕度的评估。
c.采用状态抽样法时,元件数目相对较少的RBTS的计算时间反而大于更复杂的RTS79系统的计算时间。实际上,状态抽样法在原RBTS中抽样数约为130000次,30MW风电场接入RBTS后的抽样次数约为200000次;在原RTS79系统中抽样数约为15000次,400 MW风电场接入RTS79系统后的抽样次数约为25000次。这是因为状态抽样法的评估时间与系统可靠性状况存在密切的关系。倘若系统可靠性较高(如RBTS),则采用状态抽样法时难以抽取到概率较小的故障事件,难以满足方差系数足够小的收敛条件,从而使得抽样次数增加、评估时间变长。同RBTS相比,RTS79系统尽管元件数目更多、系统更复杂,但是RTS79系统的可靠性更差,易于抽取到故障状态,从而满足收敛条件,因此计算时间反而更少。此外,采用状态抽样法时风电接入后的计算时间增加较多,这是因为风电接入系统之后,系统可靠性得到改善,但也使得使用状态抽样法抽取到系统故障状态的难度增加,因此风电接入后系统的评估时间增加较多。
d.无论是可靠性较高RBTS,还是可靠性较差的RTS79系统,风电场的接入并未显著影响状态持续时间法的评估时间;考虑到状态持续时间法又具有计算时间几乎与系统规模无关、便于计入风电机组强迫停运率、考虑系统运行方式的变化等特点,因此它非常适用于风电并网后的大规模电力系统可靠性评估。
3.2 风电机组故障率对充裕度评估结果的影响
考虑到蒙特卡洛方法评估结果存在不确定性以及解析方法计算结果准确性高的特点,本文选择使用解析法来研究风电机组强迫停运率对系统评估结果的影响。表5给出了RBTS和RTS79系统在风电机组强迫停运率从0%到15%变化时对应的δLOLE的变化情况。

表5 不同风电机组强迫停运率时的系统δLOLETab.5 δLOLEof system for different wind turbine FORs
由表5中结果可见,当风电机组强迫停运率在合理范围内变化时,风电机组强迫停运率对充裕度评估结果的影响很小。这是因为风电机组单机容量通常较小,因此单台或者少量台数风电机组的停运不会对系统充裕度造成较大影响。而在风电机组独立停运的假设下,大量风电机组同时停运的概率非常小,故不会对系统可靠性指标造成较大影响。为了降低编程的复杂性和节省计算时间,在计算精度要求不高的场合可以忽略风电机组强迫停运率的影响。
3.3 风速水平对充裕度评估结果的影响
图3和图4分别给出了RBTS和RTS79系统在不同的平均风速水平(即不同的威布尔尺度参数)时系统的δLOLE。从图3、4可见,风速水平对系统可靠性指标有很大影响,平均风速越高,系统可靠性指标越小。这是因为风速会影响风电场中的每一台风电机组的出力,因此对整个风电场的输出功率和系统充裕度的影响较大。同时也可看到,风速水平不同时风电机组强迫停运率对系统可靠性指标影响小的结论都成立。由此可见,系统的可靠性水平主要受风速波动的影响。

图3 不同风速水平时RBTS的δLOLE和风机强迫停运率的关系曲线Fig.3 Curves ofδLOLEvs.wind turbine FOR of RBTS for different wind speeds

图4 不同风速水平时RTS79的δLOLE和风机强迫停运率的关系曲线Fig.4 Curves ofδLOLEvs.wind turbine FOR of RTS79 for different wind speeds
4 结论
本文简单介绍了解析法、状态抽样法和状态持续时间抽样法进行发电充裕度评估的原理,提出了一种考虑风电机组随机停运的建立风电场解析模型的方法,并将其与状态持续时间法中计及风电机组随机停运时的风电场建模方法进行了比较分析。最后以RTBS和IEEE RTS79系统为例计算了相应的充裕度指标,得出了以下结论。
a.解析法计算时间随元件数目增大而急剧增加,仅适合于简单系统的可靠性评估;状态抽样法和状态持续时间抽样法计算时间与系统规模无关,但是状态抽样法与系统自身的可靠性有关,当系统可靠性越高时,状态抽样法的收敛速度越慢。
b.采用解析法和状态抽样法时,风电场建模和风电机组强迫停运率的计入都比较复杂;当系统规模较大时,采用解析法计算风电接入后的系统计算时间同风电接入前的系统计算时间相比增加得较多;当系统可靠性较高或者风电接入使得系统可靠性增高时,采用状态抽样法需要较多的模拟时间才能满足收敛条件。
c.采用状态持续时间抽样法时,风电机组强迫停运率的计入不会增加编程的复杂性,计算时间与系统规模几乎无关,且风电接入后计算时间的增加量很少。因此状态持续时间抽样法更适合用于实际的风电并网电力系统的可靠性评估。
d.在风电机组独立停运的假设下,风速的间歇性是影响系统可靠性指标的主要因素,风电机组强迫停运率在合理范围内的变化并不会对系统可靠性指标造成较大的影响,但是风电机组强迫停运率的计入将会增加编程复杂性和计算时间(尤其是采用解析法和状态抽样法时),实际计算中当计算精度要求不高时可以忽略风电机组强迫停运率的影响。
本文的研究对采用合适的评估方法研究其他间歇性能源(如光伏发电)之后的电力系统可靠性也提供了有意义的参考。

