基于临界阻抗和广度优先-条件搜索的暂降监测装置优化配置

邱玉涛 ，肖先勇 ，熊 茜 ，赵 恒 ，李 忠

（1.四川大学 电气信息学院，四川 成都 610065；2.国网四川省电力公司资阳供电公司，四川 资阳 641300）

0 引言

电压暂降是系统正常运行中不可避免的电能质量事件［1-3］，对其进行监测和评估是采取有效措施的前提［4-9］，实际中不可能也没必要对所有母线进行监测。因此，研究电网中电压暂降监测装置的优化配置是准确把握全网暂降水平的重要课题［10-18］，具有重要理论价值和现实意义。

国内外对暂降监测装置的优化配置问题开展了大量研究，主要归纳为3种方法：图论法、故障定位法、暂降可观测区域MRA（Monitor Reach Area）法。文献［11］考虑电网拓扑结构，基于图论进行监测装置配置，但仅适用于辐射型配网，未考虑暂降传播特性。文献［12］基于故障定位思想构造可观测矩阵，能对全网故障点唯一准确定位，但监测装置安装数量多，优化时间长，对IEEE 30节点系统仿真，优化配置时间至少需3 d，实用性不强。目前，国内外应用最广的是MRA法，该方法以监测装置数量最少为目标，以全网暂降可观为约束，适用于任意电网拓扑和故障类型，实用性较强。文献［13］提出了MRA原理，并以此构造暂降可观测矩阵，用0-1规划法求解，但仅考虑了母线故障和三相接地故障；文献［14-16］提出改进可观测矩阵法，减少监测盲区，其中文献［15-16］考虑了全网任意地点和故障类型引起暂降的可能性，所得暂降观测方程更准确、完备；文献［17］、［18］分别提出基于遗传算法、禁忌搜索算法的观测方程求解方法。这些方法在不同程度上提高了监测装置配置的全局最优性，但均依赖于暂降可观测矩阵，观测方程维数高、计算量大，推广应用困难。因此，降低观测方程维数、减少优化配置时间，是急需解决的问题。

本文在MRA法的基础上，引入临界阻抗和等效阻抗的概念，以此判定故障是否导致母线暂降；同时，考虑到电网内暂降传播特性，提出一种广度优先-条件搜索算法，形成暂降母线集，减少搜索母线数；然后通过合并导致相同暂降特征的故障点，构造全网暂降可观测矩阵。本文方法有效减少了计算量，降低了观测方程的维数，减少了优化配置时间。通过对IEEE 30、118和300节点系统的仿真，验证了本文方法的正确性和适用性。结果证明，与MRA法相比，本文方法在保证配置结果正确的前提下，明显减少了暂降监测装置优化配置时间。

1 MRA法的不足与对策

1.1 MRA法原理

电网暂降MRA定义为：当电网内故障引起电压暂降时，监测点能观测到的引起该暂降的故障点所在区域。基于MRA法的监测装置配置原理为：构造全网暂降可观测矩阵，建立观测方程，通过优化求解该方程确定监测方案。

设n为全网母线数，p为总故障数，任意故障类型下的全网暂降可观测矩阵Mw为：

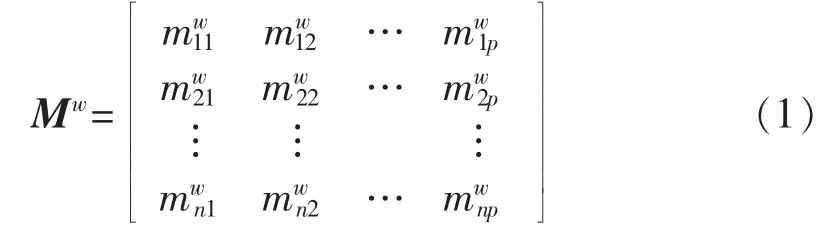
其中，w 为故障类型，取 0、1、2、3，分别表示三相接地、单相接地、两相相间和两相接地故障；Mw为n×p阶0-1二值矩阵。元素取值为：

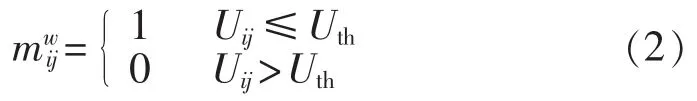
其中，i=1，2，…，n；j=1，2，…，p；Uth为监测装置设定的暂降阈值；Uij为j点故障时母线i的剩余电压值。

Mw的物理意义为：第i行元素表示母线i的MRA范围，取值为1表示故障点在MRA内，取值为0表示在MRA外；第j列元素表示j点故障引起的电压暂降可被观测的母线，取值为1表示暂降可被观测，取值为0表示不能观测。

1.2 存在的问题

基于MRA法的暂降监测装置优化配置方法，需对所有故障点、母线和可能设置的暂降阈值进行全面分析，方法复杂、繁琐。尤其在构造可观测矩阵Mw时，对每个故障点遍历所有母线，每一次遍历均需做多次计算，尤其是必须进行短路计算，其计算量很大［19］。当电网越来越复杂时，至少存在三方面问题：母线数增多，计算时间线性增长；对于任意故障点，用短路计算求各母线剩余电压均需使用母线与故障点的互阻抗和故障点自阻抗，计算量大；为避免监测盲区，可观测矩阵Mw的列数多，建立的观测方程多，导致约束条件多，优化时间长。

1.3 解决措施

以降低可观测矩阵维数、减少计算量为目标，结合MRA法存在的问题，可采取以下措施：

a.引入临界阻抗和等效阻抗的概念，作为判定母线是否暂降的条件，对于给定故障点，用故障点的自阻抗确定临界阻抗，除两相接地故障外，计算母线等效阻抗仅用母线与故障点的互阻抗，减少每次判定暂降的计算量；

b.从故障点所在线路两端母线出发，基于广度优先搜索法，仅搜索Mw中故障点所在列元素值为1的母线，并形成对应故障点的暂降母线集，其余母线对应元素值取0，减少每次被搜索的母线数；

c.合并导致相同暂降特征的故障点，降低可观测矩阵维数，减少监测装置优化配置时间。

2 基于临界阻抗与等效阻抗的Mw构造

为减少可观测矩阵构造时间，引入临界阻抗和等效阻抗的概念。以等效阻抗大于或等于临界阻抗作为判定母线暂降的条件，并确定可观测矩阵的元素取值。针对不同故障类型，给出相应的临界阻抗与等效阻抗的计算公式。

计算模型如图1所示。设m为待求母线，母线i、j之间的线路i-j故障，f为故障点，k为点f到母线i的归一化距离，确定方法如式（3）所示。k取值从 0到 1表示 f从 i到 j。

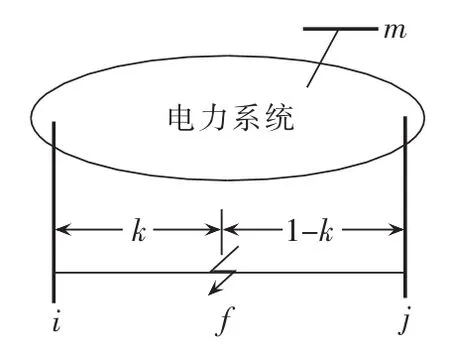
图1 电力系统短路计算模型Fig.1 Short-circuit calculation model of power system

其中，Lif为母线i到故障点f的距离；Lij为线路i-j的长度。

可见，Zmf与 k、Zmi和 Zmj有关，当故障位置和电网拓扑确定时，Zmf仅与待求母线有关；Zff与 k、zij、Zii、Zjj和Zij有关，当故障位置和电网拓扑确定时，Zff确定。

为简化计算，设各母线暂降前电压为1 p.u.（也可取实际值［20］），忽略故障阻抗影响，旋转因子 α=ej120°，当点f三相接地短路时，母线m的剩余电压Um为：

其中，abs（·）表示取有效值。

可见，Um取决于Zmf、Zff。当故障位置和电网拓扑确定时，Zff为定值，m与f的等效阻抗Zeq就是其互阻抗的模值：

其中，mod（·）表示取模值。

设暂降阈值为Uth，由式（6）可得临界阻抗Zcrit：

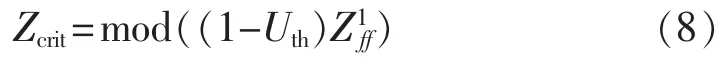
如果发生不对称故障，可用对称分量法进行分析，取幅值最小一相的电压作为等效剩余电压。

通过等效剩余电压和暂降阈值可得不同故障类型对应的临界阻抗Zcrit和等效阻抗Zeq，如式（9）—（14）所示。

a.单相接地故障。

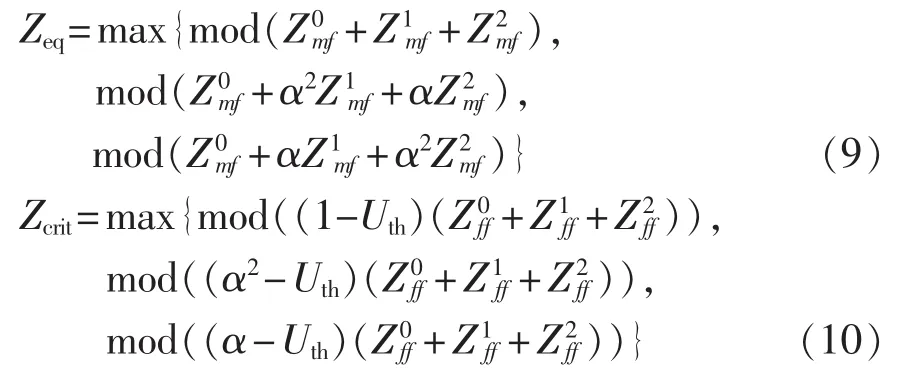
b.两相相间故障。

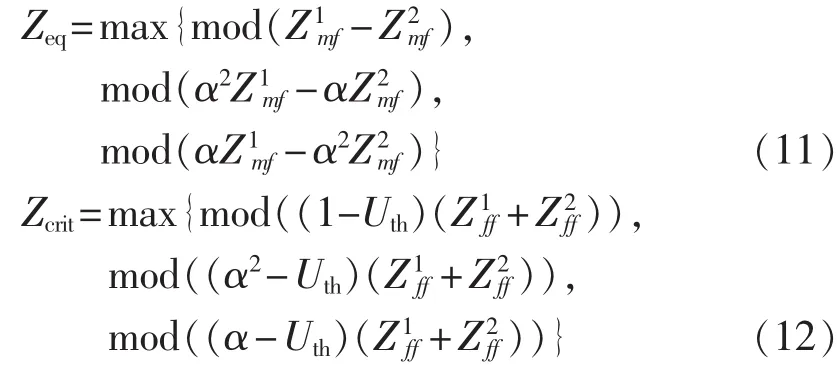
c.两相接地故障。

比较Zeq和Zcrit可判定母线是否暂降，见式（15）：

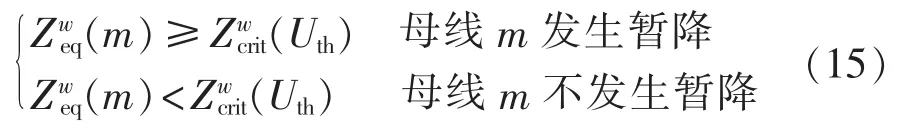
式（15）对应于式（2），但无需进行短路计算，仅用阻抗大小进行判定。

由式（7）、（9）、（11）和（13）可知，发生两相接地故障，求Zeq时需用Zmf和Zff，其他类型故障仅需用到Zmf；而MRA法对所有故障类型进行短路计算时，均需用到Zmf和Zff。表1给出了构造Mw中某列元素时使用阻抗的次数。假设全网n条母线，给定故障引起暂降的母线 n1条，显然，n1≤n。

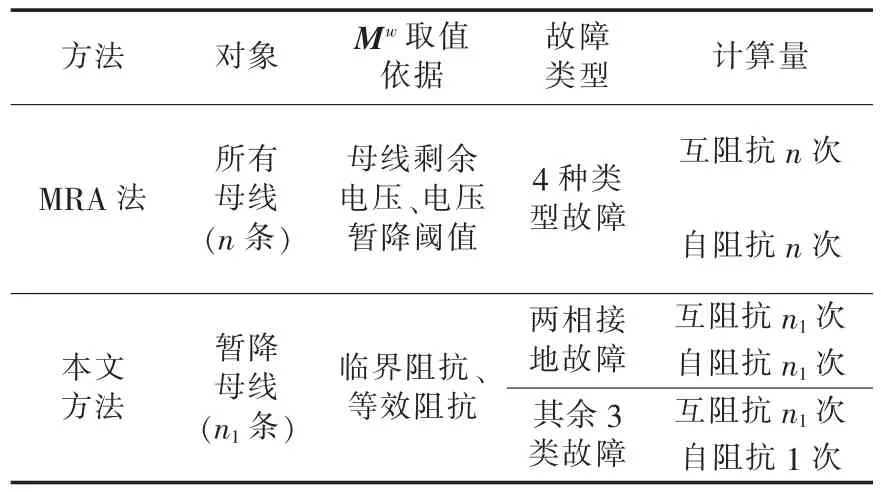
表1 构造Mw某列元素的比较Table 1 Comparison of Mwcolumn elements between two methods

可见，MRA法对任意故障类型构造Mw矩阵的每一列均需计算2n次；本文方法，两相接地故障计算2n1次，其余3类故障仅计算n1+1次，计算量明显减少。

3 暂降母线集广度优先-条件搜索

全网任意地点故障均可能引起母线电压降低，但并非所有母线均发生可观测暂降。引起可观测暂降的故障仅在MRA范围内。监测装置设定的暂降阈值越小，MRA越小。因此，当暂降阈值和电网拓扑确定时，给定故障点对应的发生可观测暂降的母线确定，这些母线可构成一个集合，定义为暂降母线集。优化配置监测装置时，仅需对暂降母线集进行搜索，其余母线不用搜索，就可大量减少计算量。从故障引起暂降的角度看，电网是一有向图。因此，提出一种广度优先-条件搜索法进行监测装置优化配置。从故障点所在线路两端母线出发，逐层搜索暂降母线，形成暂降母线集。以图2给出的IEEE 9节点系统为例，设母线7、8间线路7-8发生三相接地故障，f为故障点，故障归一化距离k=0.5 p.u.，暂降阈值Uth=0.8 p.u.。算法步骤如下：

a.由式（8）计算给定故障点f的临界阻抗Zcrit；

b.由式（7）计算故障线路首端母线7与故障点f的等效阻抗Zeq，由式（15）判定母线7是否发生可观测暂降，若发生则从母线7开始搜索下一层母线，否则停止搜索；

c.用广度优先搜索法逐层搜索与母线7有可达路径的母线，为保证每条母线仅被访问一次，可采用哈希表进行判重［21］；

d.每搜索一条母线均用式（15）进行判定，若未发生可观测暂降，则对该母线剪枝，否则继续搜索；

e.若故障线路末端母线8已被搜索，全部搜索过程结束，否则从母线8开始再次搜索，重复步骤b—d；

f.由搜索所得母线构造暂降母线集。

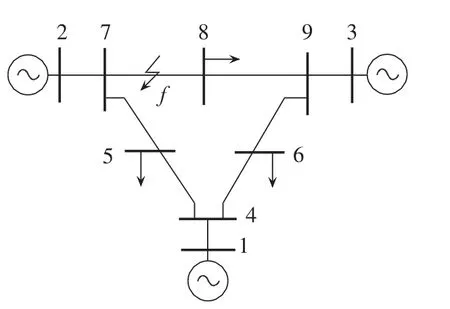
图2 IEEE 9节点系统Fig.2 IEEE 9-bus system

4 暂降监测装置优化配置算法

对任意类型故障，各线路等间距取e个故障点，全网共设置p个故障点。用上述方法确定p个故障点的暂降母线集。若同一线路上相邻2个及以上故障点的暂降母线集相同，说明这些故障点导致相同的暂降特征，则合并这些故障点，得全网q个故障点（q≤p）及其暂降母线集，Mw中故障点所在列的元素如果包含于暂降母线集，元素取值为1，否则为0。这样，Mw变为n×q阶0-1二值矩阵，针对所有故障类型的全网暂降可观测矩阵M为：

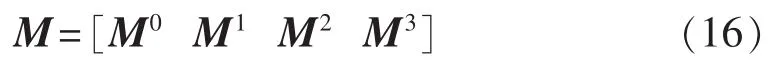
其中，M0、M1、M2、M3分别为三相接地、单相接地、两相相间和两相接地故障对应的暂降可观测矩阵，列数分别为 q1、q2、q3和 q4。

设全网n条母线，配置监测装置的决策向量为：

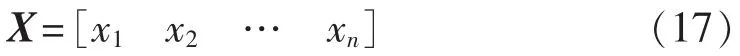
X的元素取值为：

其中，i=1，2，…，n。

以监测装置安装数量最少为目标，构造优化配置的目标函数：

以任意位置的任意类型故障引起的暂降至少能被1台装置监测为约束条件，构造观测方程为：

其中，j=1，2，…，q1+q2+q3+q4。

由式（19）、（20）构成的优化问题，可用 0-1 规划法求解。优化配置流程如图3所示。

图3 全网电压暂降监测装置优化配置流程图Fig.3 Flowchart of optimal system-wide voltage sag monitor placement

5 算例分析

为验证本文方法的正确性和适用性，在相同仿真条件下，用本文方法分别对IEEE 30、118和300节点系统进行仿真，并与文献［15-16］方法相比较。

仿真用计算机的配置参数：Intel（R）Core（TM）2 Duo CPU E7500@2.93GHz，2GB 内存；采用 Microsoft Windows XP Professional操作系统；仿真软件采用MATLAB 2008a版本。

5.1 IEEE 30节点系统仿真

对文献［16］给出的IEEE 30节点系统（IEEE 30 RTS）进行仿真。系统共30条母线、37条线路，各线路等间距取20个故障点。考虑母线和线路发生任意类型故障，得所有故障点的暂降母线集，合并导致相同暂降特征的故障点，形成全网暂降可观测矩阵。

暂降阈值分别取 0.9 p.u.、0.8 p.u.和 0.7 p.u.，得任意类型故障的监测装置优化配置结果，与文献［15-16］方法所得结果比较，如表2所示。

表2 不同暂降阈值监测装置优化配置结果Table 2 Results of optimal sag monitor placement for different sag thresholds

可见，不同暂降阈值下，本文方法所得结果与文献［15-16］方法一致，证明本文方法正确。

暂降阈值分别取 0.9 p.u.、0.8 p.u.和 0.7 p.u.时，本文方法的配置总时间分别为3.31 s、2.76s和2.48s，而文献［15-16］方法的时间分别为 10.53 s、10.86 s和11.22 s。本文方法所用时间至少减少了68.6%。

5.2 IEEE 118节点系统仿真

对文献［15］给出的IEEE118节点系统（IEEE118 RTS）进行仿真。系统共有118条母线、170条线路。各线路等间距取20个故障点，暂降阈值分别取0.9 p.u.、0.8 p.u.和 0.7 p.u.，本文方法和文献［15-16］均采用0-1规划法求解式（19）和（20），可观测矩阵构造时间tc、可观测矩阵列数q、0-1规划法优化时间to和监测装置优化配置总时间tt如表3所示。

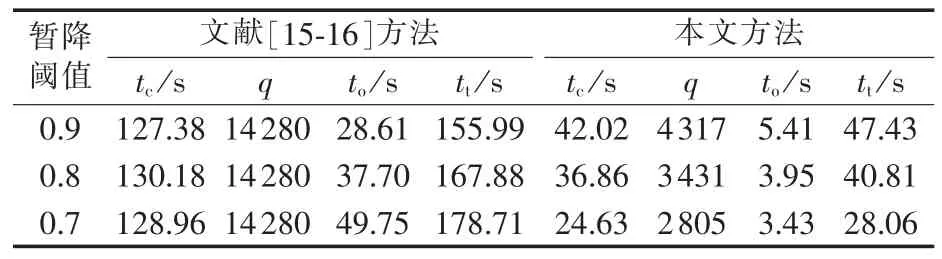
表3 不同暂降阈值计算时间Table 3 Calculation time for different sag thresholds

5.3 IEEE 300节点系统仿真

对文献［22］给出的IEEE300节点系统（IEEE 300 RTS）进行仿真。系统共300条母线、411条线路。暂降监测装置优化配置时间如表4所示。

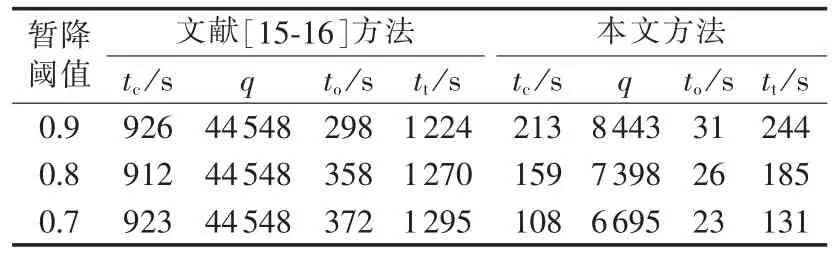
表4 不同暂降阈值计算时间Table 4 Calculation time for different sag thresholds

暂降阈值分别取0.9 p.u.、0.8 p.u.和0.7 p.u.时，对IEEE 118节点和300节点系统进行仿真，并与文献［15-16］方法比较。图4和图5分别为可观测矩阵构造时间和监测装置优化配置总时间减少的百分比。

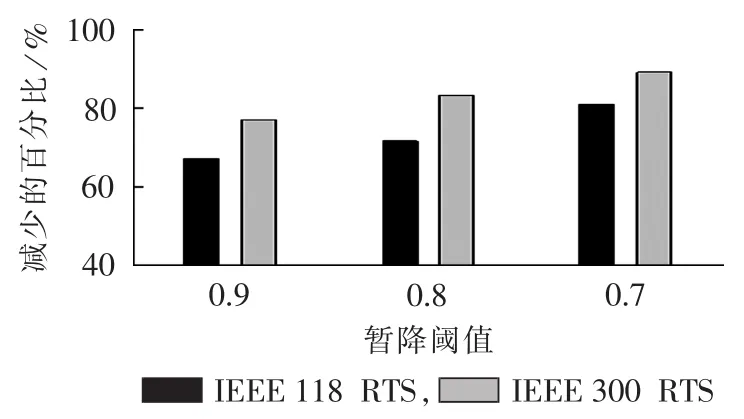
图4 可观测矩阵构造时间减少的百分比Fig.4 Percentages of time consumption reduction for observability matrix construction

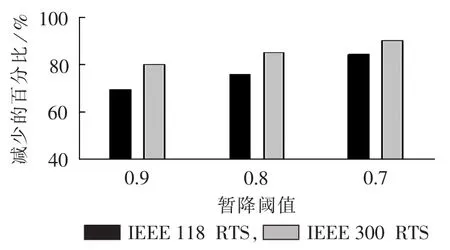
图5 暂降监测装置配置时间减少的百分比Fig.5 Percentages of time consumption reduction for sag monitor placement

5.4 仿真分析

监测装置优化配置总时间主要取决于可观测矩阵构造时间和暂降观测方程求解时间。由表3和表4可知，可观测矩阵构造时间是0-1规划优化时间的8倍左右，即优化配置时间主要取决于可观测矩阵构造时间。文献［17］、［18］分别用遗传算法和禁忌搜索算法求解暂降观测方程，未改进可观测矩阵的构造方式，监测装置配置时间变化不明显。本文改进了可观测矩阵的构造方式，降低了可观测矩阵的维数，明显减少了监测装置配置时间。

对于不同暂降阈值，文献［15-16］方法的配置时间基本不变，而本文方法随着阈值降低，所需时间越来越少。这是因为阈值越低，故障点所触发的暂降母线数就越少，广度优先-条件搜索形成的暂降母线集中母线数减少，因而可观测矩阵构造时间相应减少。

由图4、图5可知，IEEE 118节点和300节点系统的仿真结果均证明了本文方法的有效性，且电网规模越大，优势越明显。

6 结论

a.基于广度优先-条件搜索算法的暂降监测装置优化配置方法正确，可有效降低可观测矩阵的维数和减少优化配置时间；

b.用临界阻抗和等效阻抗判定暂降母线，并搜索暂降母线集，避免了遍历全网所有母线进行短路计算，有效减少了计算量；

c.合并导致相同暂降特征的故障点，降低了暂降可观测矩阵的维数，减少了优化配置时间；

d.电网规模越大，本文方法对优化配置时间的改进效果越明显，有一定工程应用价值。

本文方法有效降低了可观测矩阵维数，避免了不必要的计算，减少了监测装置优化配置时间。如何将该方法应用于实际，是下一步研究的课题。