复杂网络中修复策略研究

郑力明，李晓冬，罗建禄，韩贵杰

（1.武警警官学院 电子技术系，四川 成都 610213；2.武警警官学院 科研部，四川 成都 610213）

现实世界中的各种复杂网络，如社会网络（朋友关系网络、合作网络）、技术网络（Internet、电力网）、生物网络（神经网络、食物链网络）等[1-3]，已在人类社会生活中扮演着越来越重要的角色。然而复杂网络结构属性的不同可能在网络中节点出现故障后引起拓扑结构的极大变化，甚至是整个复杂网络的瘫痪，因此如何提高复杂网络抗毁性成为国内外研究的重点。Albert等人[4]的研究表明，无标度网络相对于随机网络，在随机打击条件下，前者具有更好的抗毁性，在故意打击条件下，后者具有更好的抗毁性。尽管可以通过优化网络拓扑结构以提高网络抗毁性，但是采用此类被动防御的措施在面对频繁密集的打击时仍然会造成整个网络的瘫痪，因此节点失效后需要尽快修复以保证网络连通性。

池丽平等人[5]提出了在随机网络和无标度网络中节点受到故意攻击后的修复模型，该模型分两步，第一步找出网络中度最大的节点并将该节点与其他所有节点的连接断开，第二步该节点以固定的概率与网络中其他节点重新建立连接。通过不断重复上述步骤以研究网络的稳定性。池丽平等人的研究结果表明在随机网络中，网络的稳定性与随机网络的平均度呈幂律分布；在无标度网络中，网络的稳定性与修复概率呈指数分布。然而在实际网络中，受资源限制，每个节点可被修复的概率是不同的，且总的修复能力也是有限的。

胡斌等人[6]考虑到了实际网络中资源受限，并提供平均修复策略，重点修复策略和偏好修复策略以对比在不同网络攻击中的修复能力。其修复模型分两步：第一步找出网络中度最大的节点并将该节点与其他所有节点的连接断开，第二步该节点根据修复策略所对应的概率恢复原来的连接。对无标度网络的实验结果表明，偏好修复的鲁棒性较好。然而在实际网络中，节点的修复需要一定的时间，这对网络的打击效果和修复效果都会产生影响。

本文提出一种延迟修复的复杂网络修复模型，在此基础上定义了多种修复策略，最后给出在随机打击和故意打击情况下各种修复策略的修复能力。

1 修复模型和修复策略

1.1 修复模型

步骤1根据打击策略，从网络中选择一个被打击的节点，删除该节点与其他节点的所有连接，并对该节点的修复时间开始计时。

步骤2遍历所有被打击的节点，如果节点的修复时间到达T，则根据该节点的修复概率进行修复，节点修复后恢复原来的连接。

步骤3重复步骤1和步骤2。

1.2 修复策略

复杂网络的修复策略事实上是指各个节点的修复因子的分配策略，由于网络中的总修复因子受限，而各个节点的重要程度各不相同，在不同的打击环境下受关注的程度也各不相同，因此通过分配有限的修复因子以提高网络的抗毁性。其主要的修复策略包括：

1）平均修复（uniform strategy）：各个节点的修复因子P都相同，即P=M/N。

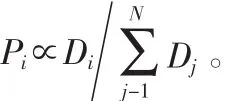
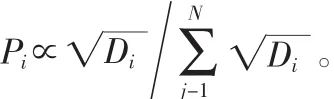
2 模拟测试

为了验证各种修复策略在不同的网络拓扑下的修复能力，实验中模拟实现了规模为1000的随机网络和BA网络两种网络拓扑，为了验证各种修复策略应对多种打击情况下的修复能力，实验中实现了随机打击和故意打击两种模式。另外，修复策略的修复能力以网络的最大连通图的大小为依据。实验中，设置总的修复因子M=10，最大修复因子Pmax=1，修复时间T=10。

2.1 随机网络

图1显示了随机网络中对节点进行连续随机打击后各种修复策略的修复效果，其修复效果由强到弱依次为：均匀修复、平方根修复、比例修复、平方修复。在随机打击中，由于节点是随机选择的，因此均匀修复能够很好的照顾到每个节点，实验显示网络的最大强连通图的比例稳定在91%以上；在随机网络中各个节点的度服从泊松分布，因此比例修复下各个节点的修复概率差别不大，实验显示网络的最大强连通图的比例稳定在88%以上；而平方根修复则是对比例修复和均匀分布的折中效果，一方面考虑了节点度对修复概率的影响，另一方面也照顾到节点的公平性，其最大强连通图的比例稳定在90%以上；最后平方修复是在尽量扩大节点度对修复概率的影响程度，因此在随机选择度较小的节点后，其修复的概率也较小，其最大强连通图的比例稳定在85%以上。

图2显示了随机网络中对节点进行连续故意打击后各种修复策略的修复效果，其修复效果由强到弱依次为：平方修复、比例修复、平方根修复、均匀修复。在故意打击中，每次选择系统中度最高的节点，这样均匀修复中度高的节点被修复的概率就相对较小，实验显示网络的最大强连通图的比例稳定在86%以上；比例修复考虑了节点度对修复概率的影响，因此度高的节点被修复的概率较大，网络的最大强连通图的比例稳定在92%以上；而平方根修复则是对比例修复和均匀分布的折中效果，其最大强连通图的比例稳定在89%以上；最后平方修复是在尽量扩大节点度对修复概率的影响程度，因此能够重点保护度较高的节点，其最大强连通图的比例稳定在94%以上。

综上可以看出，对于随机网络，在不确定对方的打击模式的情况下，采用比例修复或者平方根修复能够达到较好的修复效果，而均匀修复和平方修复则只能针对特定的一种打击模式具有较好效果。

图1 随机网络随机打击下的修复效果Fig.1 Random attack by random network repairing effect

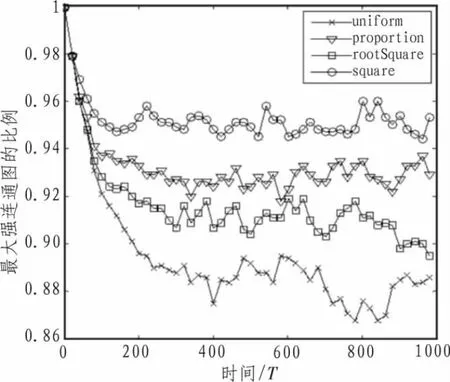
图2 随机网络故意打击下的修复效果Fig.2 Intentional attack by random network repairing effect

2.2 无标度网络

图3显示了BA网络中对节点进行连续随机打击后各种修复策略的修复效果，其中均匀修复和平方根修复几乎具有同样好的修复效果，其次为比例修复，最差的是平方修复。在随机打击中，由于节点是随机选择的，因此均匀修复很好的照顾到每个节点，其最大强连通图的比例稳定在88%以上；在BA网络中各个节点的度服从幂律分布，因此比例修复下各个节点的修复概率差别较大，实验显示网络的最大强连通图的比例稳定在85%以上；而平方根修复则是对比例修复和均匀分布的折中效果，一方面考虑了节点度对修复概率的影响，另一方面也照顾到节点的公平性，其最大强连通图的比例稳定在87%以上；最后平方修复是在尽量扩大节点度对修复概率的影响程度，因此在随机选择度较小的节点后，其修复的概率会非常小，其最大强连通图的比例随时间一直减小。

图4显示了BA网络中对节点进行连续故意打击后各种修复策略的修复效果，其修复效果由强到弱依次为：平方修复、比例修复、平方根修复、均匀修复。在故意打击中，每次选择系统中度最高的节点，这样均匀修复中度高的节点被修复的概率就相对较小，另外BA网络中度高的节点对网络的连通性影响很大，实验显示网络的最大强连通图的比例随时间急剧减小；比例修复考虑了节点度对修复概率的影响，因此度高的节点被修复的概率较大，网络的最大强连通图的比例稳定在88%以上；而平方根修复则是对比例修复和均匀分布的折中效果，其最大强连通图的比例稳定在92%以上；最后平方修复是在尽量扩大节点度对修复概率的影响程度，因此能够重点保护度较高的节点，其最大强连通图的比例稳定在94%以上。

综上可以看出，对于BA网络，在不确定对方的打击模式的情况下，采用平方根修复能够达到较好的修复效果，其次为比例修复，而均匀修复和平方修复则只能针对特定的一种打击模式具有较好效果。

图3 无标度网络随机打击下的修复效果Fig.3 Random attack by scale-free network repairing effect

图4 无标度网络故意打击下的修复效果Fig.4 Intentional attack by scale-free network repairing effect

3 结束语

文中针对复杂网络修复问题，首先提出了一种延迟修复的网络修复模型，并在不同复杂网络拓扑下针对随机打击和故意打击提出了四种不同的修复策略，模拟实验结果显示在随机网络下，采用比例修复或者平方根修复能够达到较好的修复效果；而在无标度网络下，采用平方根修复能够达到较好的修复效果。

[1]Albert R，Barabasi A L.Statistical mechanics of complex network[J].Review of Modern Physics，2002，74（1）:47-97.

[2]S.Ratnasamy， P.Francis， M.Handley EA.A Scalable Content-Addressable Network [C]//In: Proc. of ACM SIGCOMM.New York，USA:2001.149-160.

[3]Watts D J，Strogatz S H.Collective dynamics of small-world networks[J].Nature，1998，393（4537）:440-448.

[4]Albert R，Jeong H，Barabasi A L.Error and attack tolerance of complex networks[J].Nature，2000，406（6794）:378-382.

[5]Chi L P，Yang C B，Cai X.Stability of random networks under evolution of attack and repair[J].Chinese Physics Letters，2006，23（1）:263-266.

[6]胡斌，黎放.多种攻击策略下无标度网络修复策略[J].系统工程与电子技术，2010，32（1）:43-47.

HU Bin，LI Fang.Multiple attack strategy scale-free network repair strategy[J].Systems Engineering and Electronics，2010，32（1）:43-47.