特定谐波消除法在T型三电平并网逆变器中的应用

张扬帆，严 成，邹莘剑，陈 敏，徐德鸿

（浙江大学电气工程学院，杭州 310027）

引言

PWM调制方式作为并网逆变器中的关键技术，一直是研究的热点［1］。相比于正弦波PWM调制（SPWM）和空间矢量调制（SVPWM）方法，特定谐波消除法（SHEPWM）具有开关频率低、输出电压质量好及损耗小等一系列优点［2］。

近年来，SHEPWM调制法已经应用于电机调速［3］、DSTATCOMs［4］等电力变换场合。 文献［5］在NPC型三电平拓扑上应用了两种SHEPWM调制方式（C-SHEPWM和M-SHEPWM）的混合调制策略，实现了对电机调速系统共模电压抑制的效果。文献［6］在NPC拓扑上通过对SHEPWM调制法开关角的小调整，来控制母线中点电压的波动。

本文介绍了应用于T型三电平并网逆变器的特定谐波消除法（SHEPWM）调制方法。比较特定谐波消除法（SHEPWM）与空间矢量调制（SVPWM）两种调制方式对逆变器并网电流谐波和效率的影响，并在10 kW T型三电平并网逆变平台上进行了实验验证。

1 SHEPWM调制方式

1.1 SHEPWM基本原理

三电平逆变器采用SHEPWM调制方式时，通常假设输出波形具有1/4周期对称和关于π/2偶对称［7］，T型三电平电路的A相输出相电压及开关管驱动波形如图1所示。其中Vdc为直流母线电压，Va1为相电压基波，α1，α2，…，αN为 1/4 基波周期开关角，gsai（i=1,2,3,4）表示理想情况下各开关管Sai的驱动波形，T型三电平主电路如图4所示。

对三电平电路相电压波形傅里叶分解，得

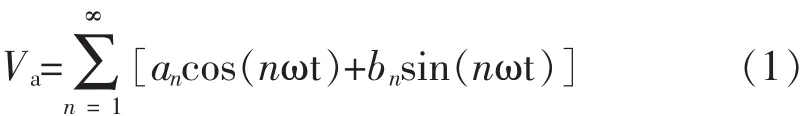
由波形的对称性，可知输出相电压的傅里叶分解中所有的余弦分量均为0，即an=0，而正弦分量的表达式为

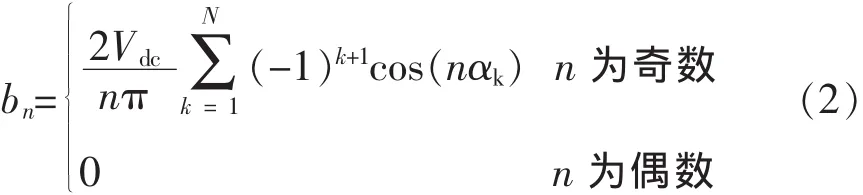
定义幅度调制比m为逆变器输出相电压基波幅值b1与直流母线电压Vdc的一半的比值，即

这样，当1/4周期开关角个数为N时，可以得到N个独立的方程，以控制基波幅值和消除N-1个谐波含量。考虑到三电平主要用于大功率逆变器，一般为三相系统，故只需消除低频次谐波中的非3倍频次谐波。根据式（2），可以得到1/4周期开关角个数为N（N为奇数）时求取开关角的非线性方程组为

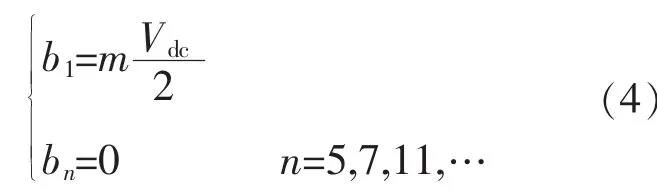
由式（4）可知，当N为奇数时，SHEPWM可以消除的最高次谐波为3N-2次。

由图1的开关管驱动波形可知，对于T型三电平逆变器，在输出相电压的正半周，开关管Sa1和Sa3互补PWM输出，而开关管Sa2一直关断，Sa4一直导通；而在输出相电压的负半周，开关管Sa2和Sa4互补PWM输出，而开关管Sa1一直关断，Sa3一直导通。可见，对于T型三电平逆变器，只需将离线求解得到的1/4基波周期下不同m值的开关角存储到DSP控制器的内存中，再根据闭环调制需要的m值进行查表，由对称性即可得到一个基波周期内各开关管的驱动波形。同理可以得到另外两相（B、C相）的开关管驱动波形，从而完成对T型三电平逆变器的调节，实现SHEPWM调制法。

1.2 开关角求解

对应用于并网逆变器的特定谐波消除法，首先需要对开关角的个数进行选取，其原则如下：

（1）选择的开关角满足并网电流总谐波和各次谐波要求［8］，以满足并网标准；

（2）开关角个数尽可能少，以减少存储空间。

需要注意的是，由于采用的为LCL滤波器，故SHEPWM的剩余最低次谐波应大于谐振频率，防止谐振频率处的电压谐波引起很大的谐振电流。

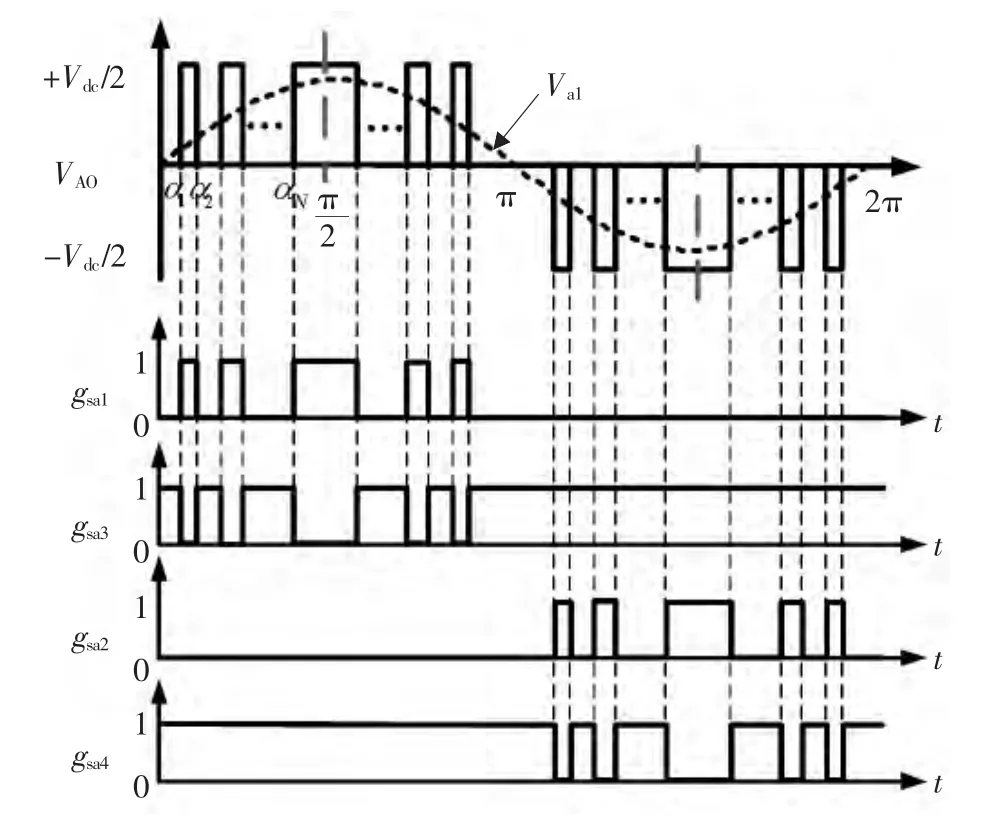
图1 三电平SHEPWM相电压及驱动波形

本文所述的逆变器参数如表1所示。此时LCL滤波器的谐振频率为

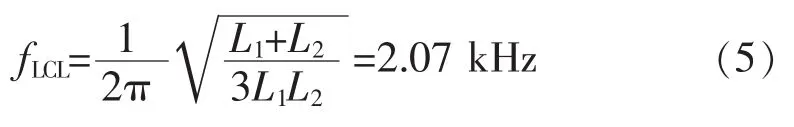
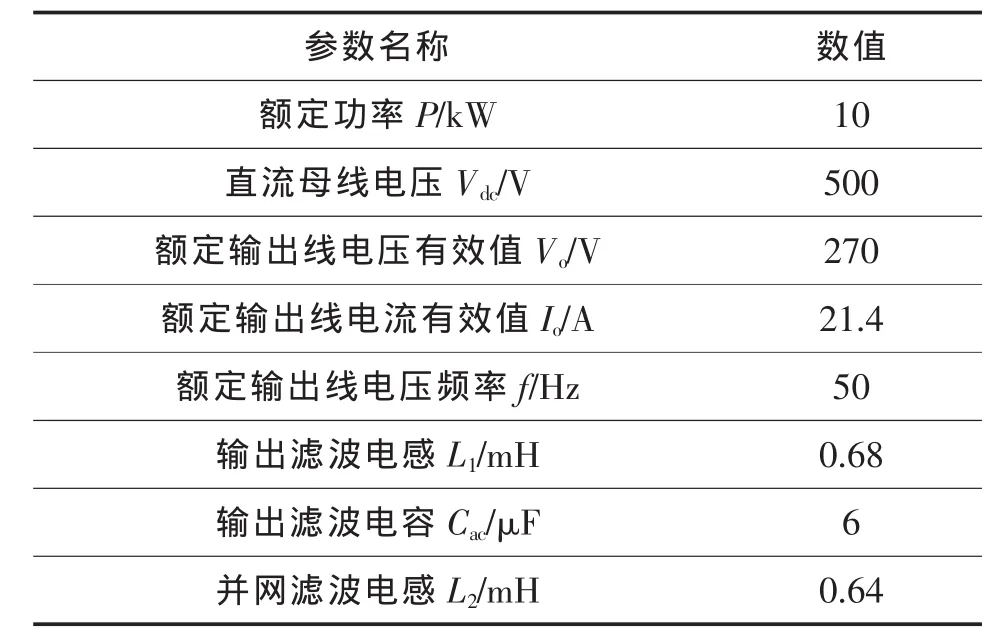
表1 逆变器参数表

由式（4）可知，当1/4周期开关角个数N为奇数时，SHEPWM可以消除的最高次谐波为3N-2次，故应满足

式中，f0为基波频率，在表1所示的参数下，由式（6）得

取整得到N的最小值为15。考虑一定的裕量，计算了1/4周期开关角个数分别为N=17、N=21、N=25和N=29时的并网电流频谱分布，如图2所示。其中并网电流谐波最高次计算到85次。

由图2可以得知：（1）当开关角个数为N时，SHEPWM调制法并网电流中3N-2次以内的谐波基本被消除；（2）N=17时，并网电流总谐波THD=11.4%；N=21时，并网电流总谐波THD=5.5%，不满足并网要求；（3）N=25时，并网电流总谐波THD=3.2%，但第79次、83次并网电流谐波不满足并网各次谐波要求；（4）N=29时，并网电流总谐波THD=0.48%，且各次并网电流谐波均满足并网要求。综上所述，本文选取了1/4周期开关角个数为N=29。

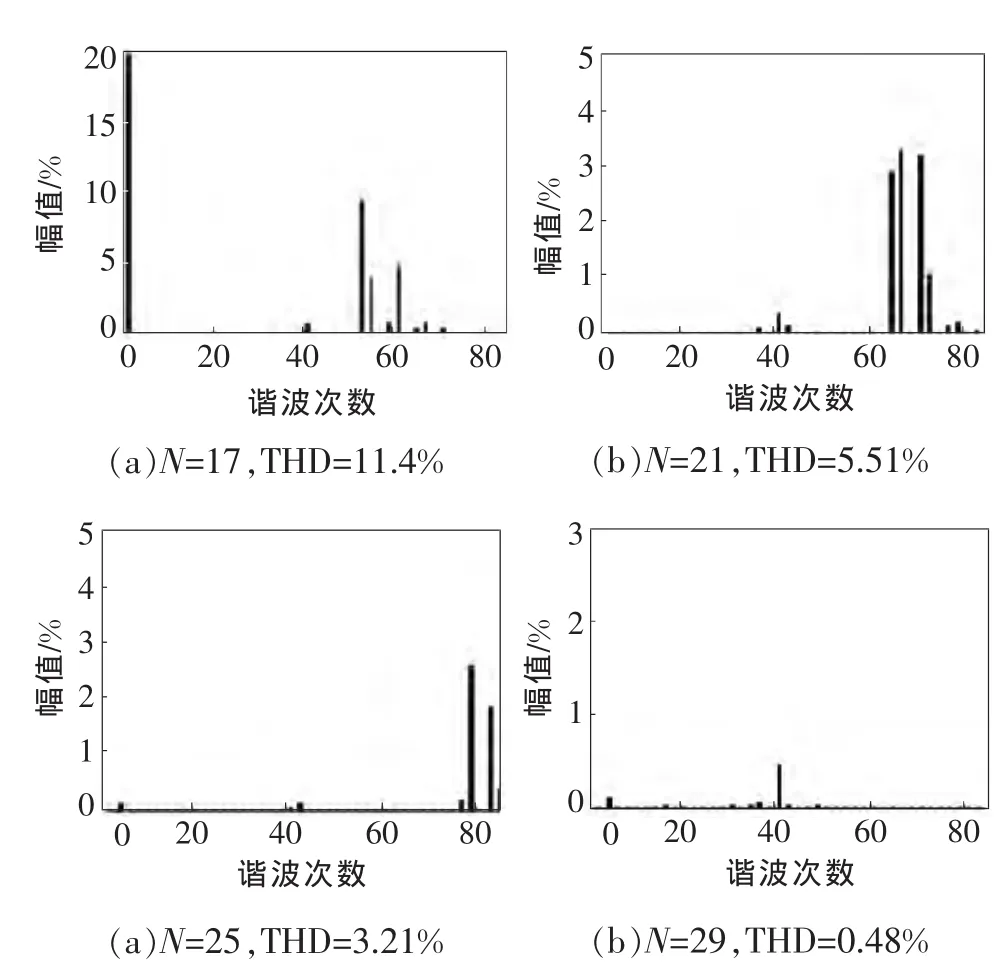
图2 不同开关角个数时并网电流谐波分布（10 kW）

选取了开关角个数后，可以对不同幅度调制比下的开关角进行求解。关于非线性方程组初值的选择有一系列的文章进行了研究，本文采用文献［9］提出的初值解经验公式法得到m=0时解的初值。在此基础上，利用Matlab中基于牛顿迭代法的fsolve函数，计算出一个在此m的基础上一个很小增量dm的解，再将得到的解作为下一次计算的初值［7］。如此逐渐增大幅度调制比m的值，可以计算出幅度调制比m从0到1，步长为0.01的开关角度，如图3所示。

由图3可知，当采用本文的开关角求解方法时，在幅度调制比m在0～0.65范围内时，开关角与调制比的曲线近似为一段直线；而当幅度调制比m在0.65～1.0范围内时，开关角与调制比的曲线为非线性的弧形曲线。

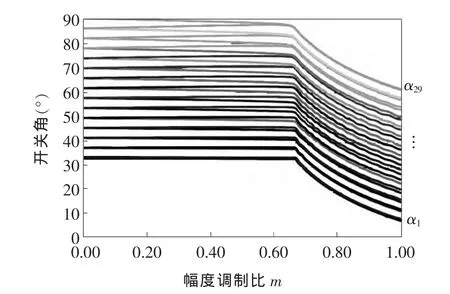
图3 开关角随幅度调制比变化曲线（N=29）

需要注意的是，由于SHEPWM非线性方程组的多解性，当采用不同的初值和不同的解法时，可得出不同开关角的解轨迹。对于不同的解，均能消除特定的低次谐波，但是高次谐波的分布会略有不同［7］。

1.3 控制环路

T型三电平并网逆变器控制框图如图4所示［3］。并网电流给定值id*和iq*与并网电流采样变换值id和iq的误差分别进行PI运算后，分别加上电网电压前馈值ugd和ugq得到ud*和uq*，再根据ud*和uq*计算得到幅度调制比m和电压电流相位角Δθ。Δθ加上电网相电压锁相相位角θg得到查表的相位角θ，最后通过幅度调制比m和相角θ查表计算后得到所需的占空比。其中电网电压前馈ugd和ugq是为了加快响应的速度。

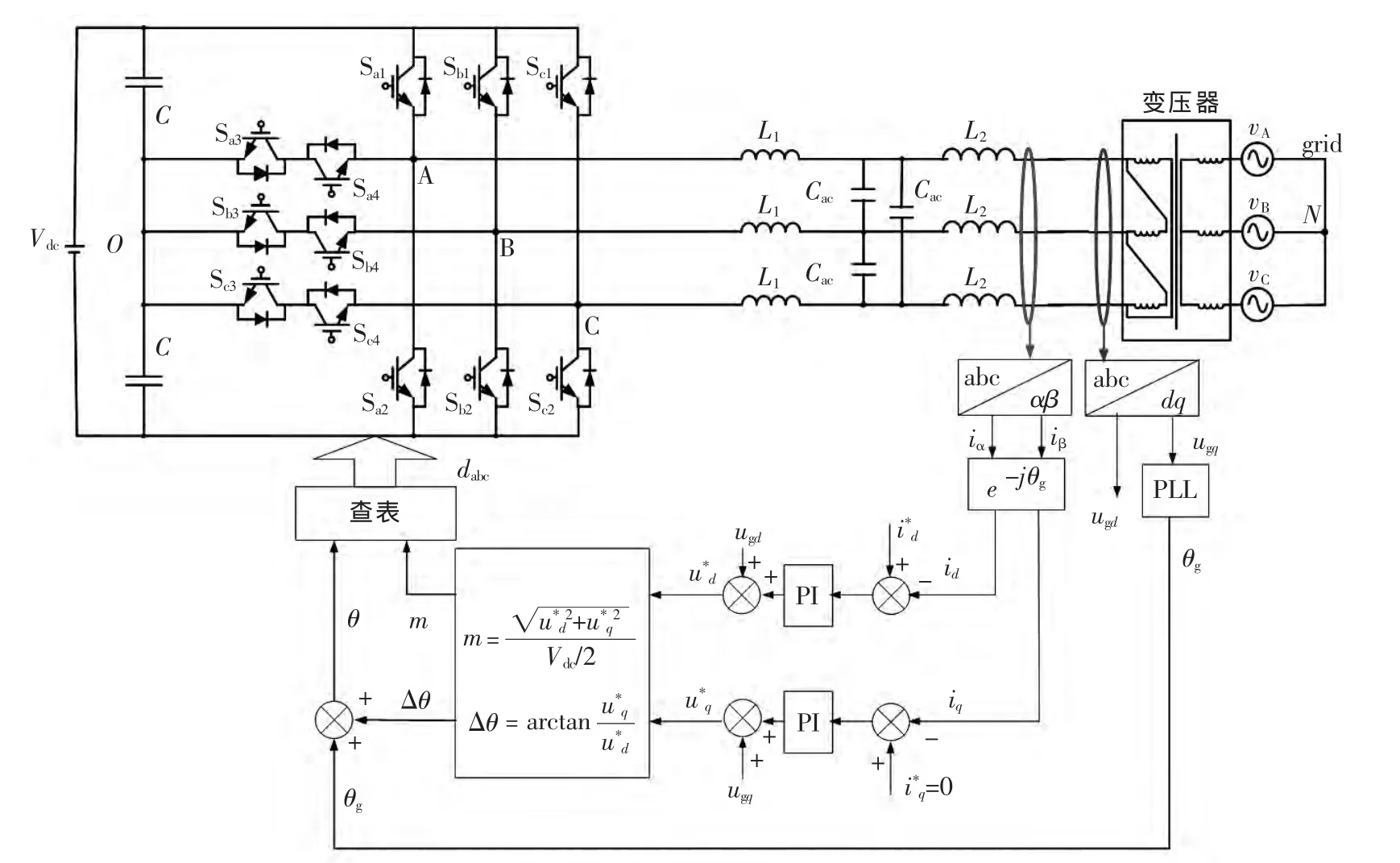
图4 T型三电平主电路及控制框图

参考SVPWM的环路设计方法，对图4所示的SHEPWM调制法的环路进行设计，得到d轴电流环的控制框图如图 5 所示［10-11］。

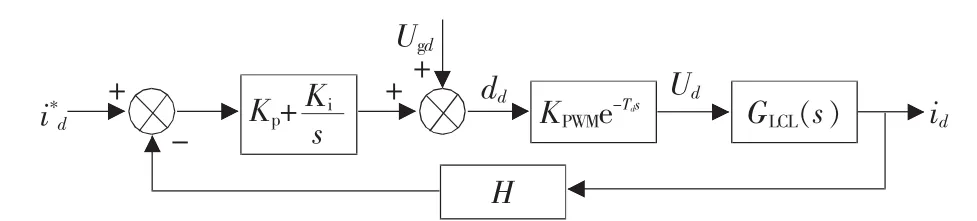
图5 电流环d轴控制框图

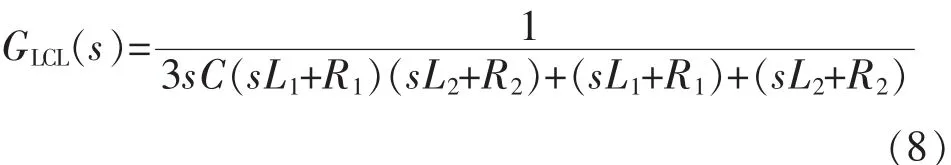
补偿前被控对象的开环传递函数为

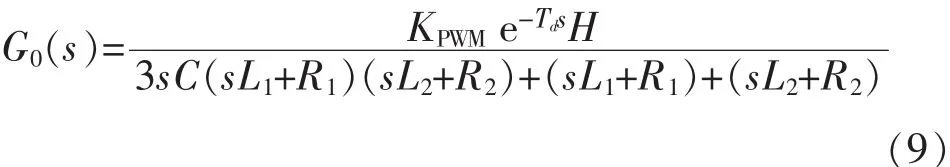
由于本文采用的SHEPWM调制法是基于一整个基波周期进行查表实现的思想，故需要一整个基波周期才调节一次调制比m和相角θ，为此需要限制环路的带宽。结合电路的具体参数，选择PI参数为 Kp=0.002 4，Ki=0.079,得到了 PI补偿前后的开环传递函数的幅频特性与相频特性曲线，如图6所示。补偿后穿越频率为4 Hz，相位裕量为 37.5°。

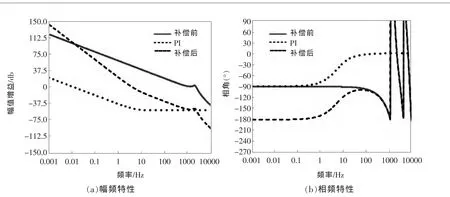
图6 补偿前后的幅频特性及相频特性图

2 谐波分析

不考虑电网电压的谐波分量时，并网电流的各次谐波分量［12］为

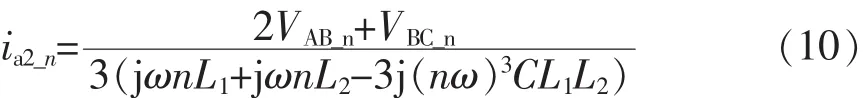
式中：VAB_n和VBC_n分别为逆变侧AB线电压和BC线电压谐波；n为谐波次数，ω为角速度；L1L2和C为滤波器参数。

为验证SHEPWM的优势，在相同的参数条件下将SHEPWM调制法和SVPWM调制法进行比较分析。其中，SHEPWM调制法的1/4周期开关角个数选取为N=29，SVPWM调制法的选取为连续调制，开关频率为fs=7.6 kHz。

由式（10）可知，当逆变器参数确定的情况下，并网电流的各次谐波仅与逆变线电压的谐波有关。对于不同调制方式，只需分析不同调制方式下的逆变线电压的谐波分量即可得知并网电流的谐波特性。由于SHEPWM调制法能消除输出相电压的低次谐波，使得逆变输出线电压的低次谐波为0，并网电流的低次谐波理论上也可以消除为0，从而并网电流的低次谐波也可以大大减小。

图7为利用Matlab进行傅里叶分解，仿真计算得到的两种调制方法的输出逆变线电压频谱。由图可以得知：1）SVPWM主要为开关次（152次）及开关的倍数次附近的电压谐波，而SHEPWM主要为剩余的最低次谐波（89次）及其倍数次附近的电压谐波；（2）SVPWM电压低次谐波较大，85次以内的电压谐波有1.88%，而SHEPWM电压低次谐波基本上被消除，85次以内的电压谐波只有0.09%，远远小于SVPWM调制法。

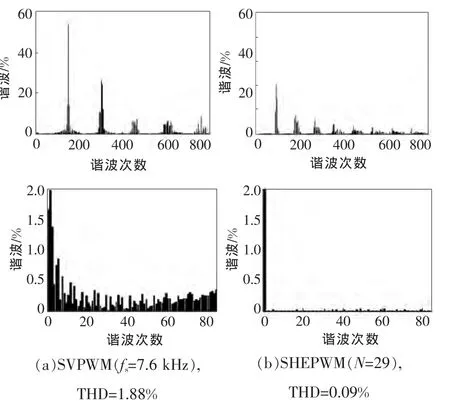
图7 SVM和SHEPWM逆变线电压谐波频谱

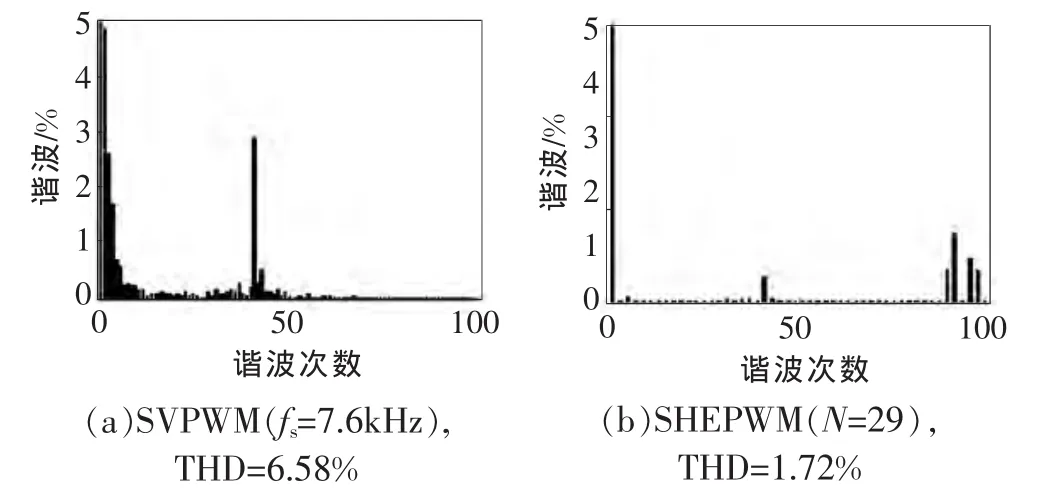
图8SVM和SHEPWM并网电流谐波频谱

图8 为Matlab仿真计算得到的两种调制方法的并网电流频谱。由图8可知，SHEPWM调制法的并网电流低次谐波只剩下LCL谐振处（40次）附近的谐波（这是由于开关角的误差等导致的），其它的低次谐波基本为0。可见，相比SVPWM调制法，SHEPWM的并网电流低次谐波要大大减小。

3 损耗分析

逆变器的损耗主要包括开关器件损耗和滤波器的损耗。其中开关器件的损耗由导通损耗和开关损耗构成，而滤波器的损耗主要由电感的铜损和铁损构成［12］。

逆变器的参数如表1所示，开关器件选用IKW40N120H3的IGBT单管。根据IGBT单管的数据手册和工作条件，可以分别计算出在SHEPWM和SVPWM两种调制方式下的桥臂IGBT导通损耗、钳位管IGBT导通损耗、钳位管二极管反向恢复损耗及IGBT开关损耗；根据额定功率及逆变侧的谐波电压，可以计算出LCL滤波器的电感铜损和铁损，最终可以得到在不同功率等级下逆变器各部分损耗分布及效率，如图9和图10所示。

由图9和图10可知：（1）在相同功率等级下，两种调制方式导通损耗基本相同；（2）SHEPWM的等效开关频率比SVPWM低，故其IGBT管的开关损耗远小于SVPWM；（3）SHEPWM的逆变电压和并网电流谐波特性比SVPWM好，故LCL滤波器的铁损比SVPWM小；（4）轻载时，器件开关损耗占的比例大，故此时SHEPWM的损耗减小的比例大，SHEPWM的效率优势更明显；重载时，器件开关损耗占的比例小，此时SHEPWM的损耗减小的比例也变小，SHEPWM的效率优势变得不太明显。

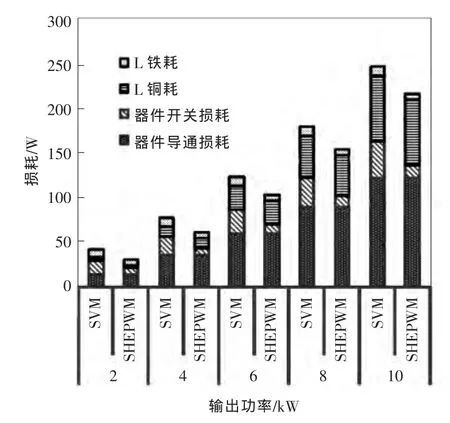
图9 逆变器损耗理论值

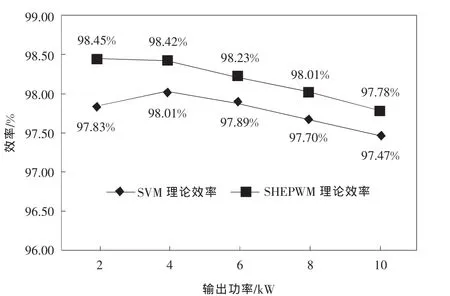
图10 逆变器效率理论值

4 电网谐波对并网电能质量的影响

实际情况下，电网电压中会存在一定量的低次谐波，特别是5、7次电压谐波。当考虑电网电压的谐波分量时，并网电流的各次谐波分量［12］为

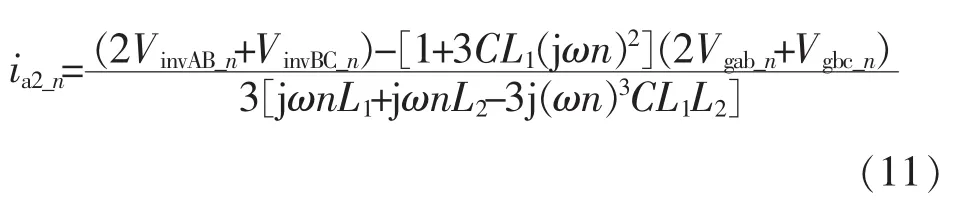
式中：VAB_n和VBC_n分别为逆变侧AB线电压和BC线电压谐波；Vgab_n和Vgbc_n分别为电网AB线电压和BC线电压谐波；n为谐波次数；ω为角速度；L1L2和C为滤波器参数。

由式（11）可知，当电网电压中含有低次谐波时，会产生相应次的并网电流谐波，影响并网电能质量。

在表1所示的参数下，Simulink仿真电网5次、7次谐波对相应次的并网电流谐波影响如图11所示。由图可以得知：（1）采用SHEPWM调制法时，当电网电压中的5次、7次谐波增大时，并网电流的5次、7次谐波也会随之增大；（2）在电网电压谐波幅值相同的情况下，5次电网谐波产生的并网电流谐波大于7次电网谐波产生的并网电流谐波；（3）SHEPWM调制法无法抑制由电网电压低次谐波引起的并网电流谐波，电网低次谐波对并网电能质量有较大的影响。

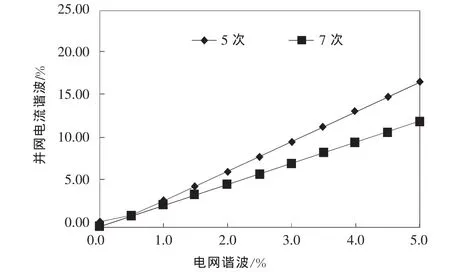
图11 仿真电网谐波对并网电流谐波影响

对于电网谐波对SHEPWM并网电能质量不利影响的改进方法，还需进一步的探讨。

5 实验

根据以上分析，在一台10 kW T型三电平逆变平台上进行了实验。实验平台的参数与理论分析时一致，主控芯片采用了DSP芯片TMS320F2808。

图12是两种调制方式在10 kW并网条件下的实验波形。其中Vinvab和Vgab分别为逆变线电压和电网线电压，ia和ib分别为A、B两相的并网电流。

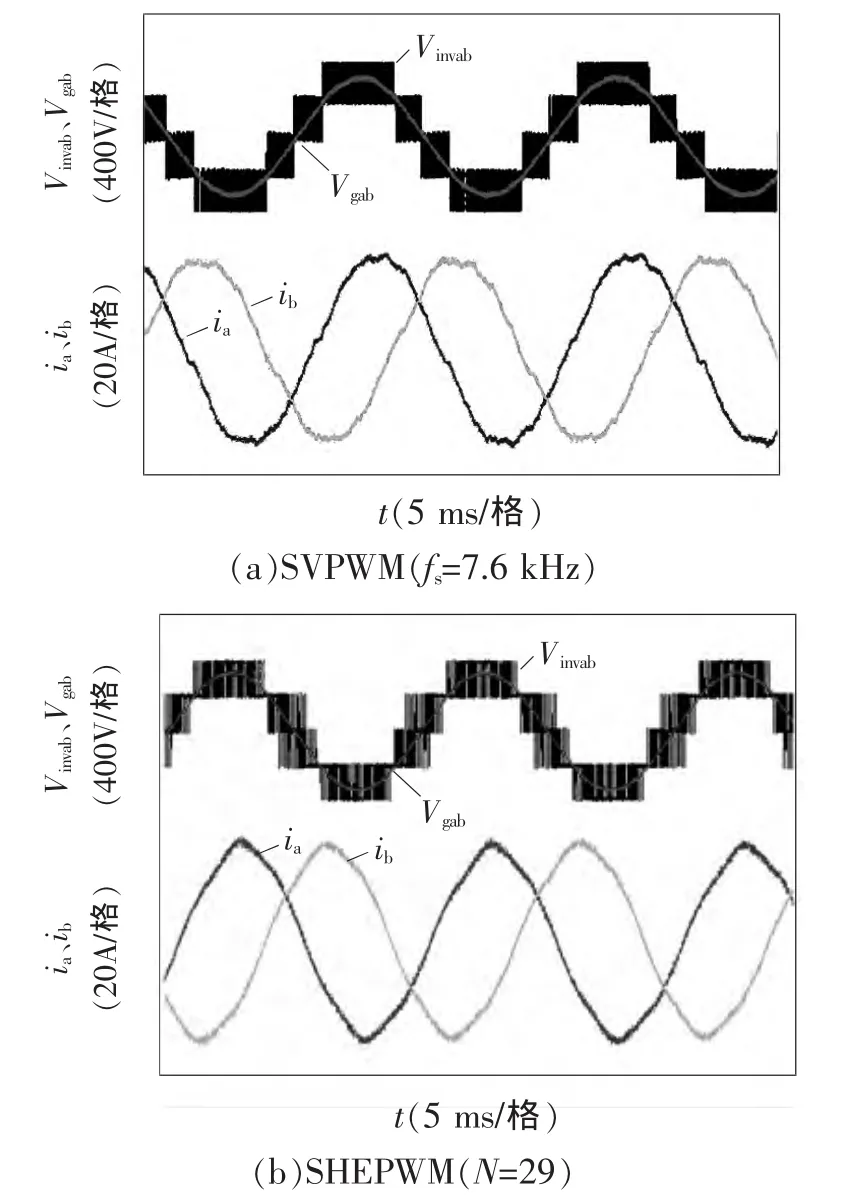
图12 10 kW并网实验波形

由图12可知，两种调制方式下，并网电流的波形和对称性都较好。相比SVPWM调制法，SHEPWM的并网电流波形较光滑，但是较大的低次谐波会影响并网电流波形。

将示波器采出的电压和电流波形经过Matlab的FFT分解得到两种调制方式在10 kW并网时的逆变线电压、并网电流的谐波频谱，如图13和图14所示。

由图13可知，SVPWM电压谐波主要分布在开关次及开关的倍数次附近，且低次谐波较大（85次以内2.33%）。而SHEPWM电压谐波主要分布在剩余的最低次谐波及其倍数次附近，且低次谐波很小（85次以内0.84%），这与理论分析基本一致。

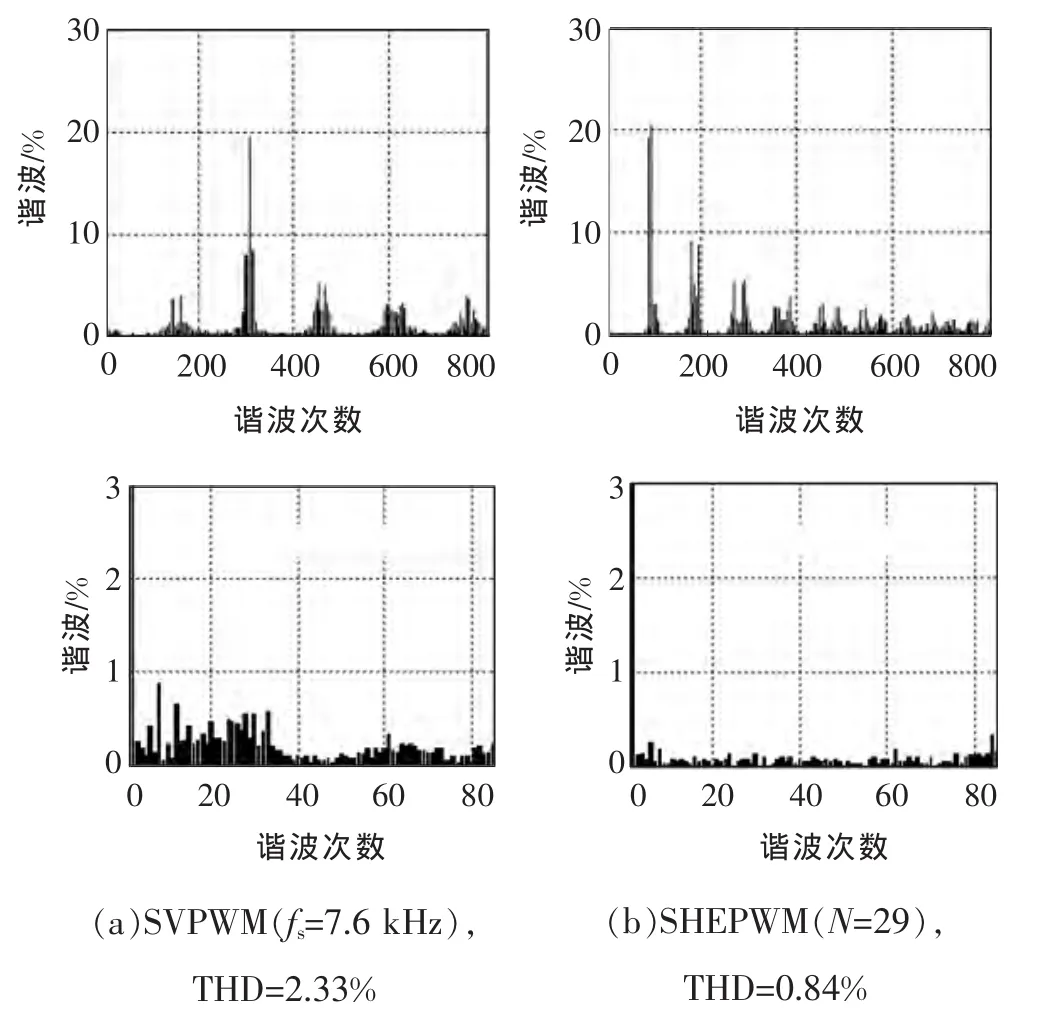
图13 10kW 实验逆变线电压谐波频谱

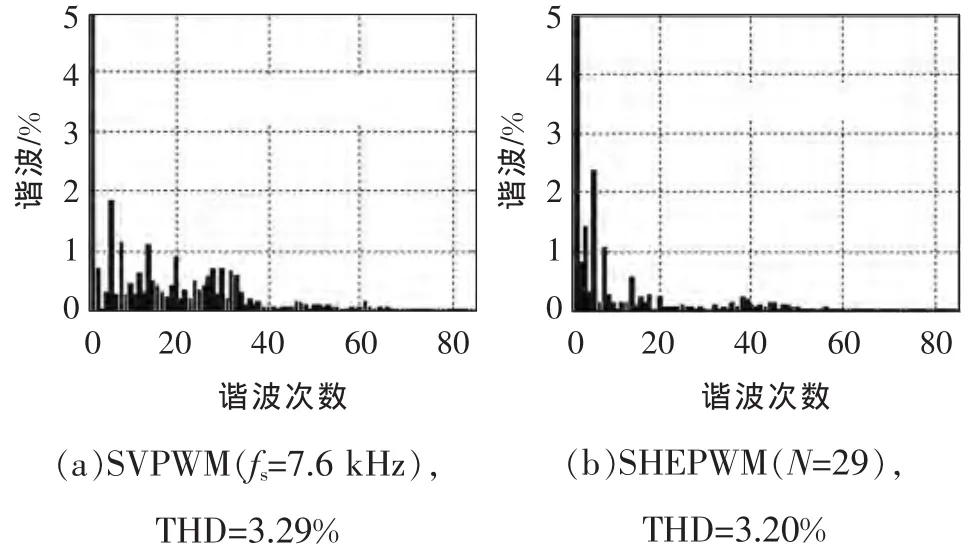
图14 10kW实验并网电流谐波频谱

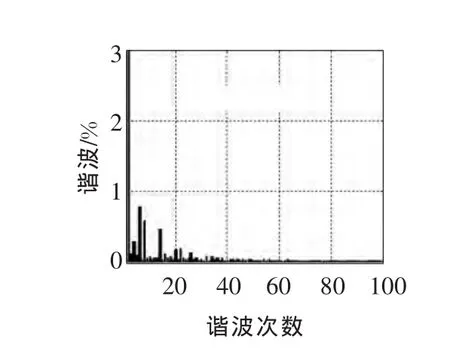
图15 电网电压频谱（THD=1.18%）

由图14可知，SVPWM由于逆变电压低次谐波的存在，导致并网电流的低次谐波也较大（85次以内3.29%）。而SHEPWM逆变电压低次谐波很小，但是由于电网的低次谐波的存在（如图15所示，85 次以内 1.18%，主要为 3、5、7 次），导致并网电流的低次谐波也较大（85次以内3.20%，主要为3、5、7次），但由于其他次的谐波基本消除，在10 kW时的并网电流THD总含量及各次谐波均满足并网标准。

图16是两种调制方式在不同功率等级并网时的并网电流THD（测量到85次）。由图可知，由于电网电压谐波引起的电流低次谐波的存在，导致SHEPWM存在电流低次谐波，两种调制方式下的并网电流总THD基本相同，逆变器在输出功率大于6 kW时电流THD总量均已经小于5%，而满载10 kW时SHEPWM的并网电流THD为3.26%，SVPWM的并网电流THD为3.20%，均满足并网标准。

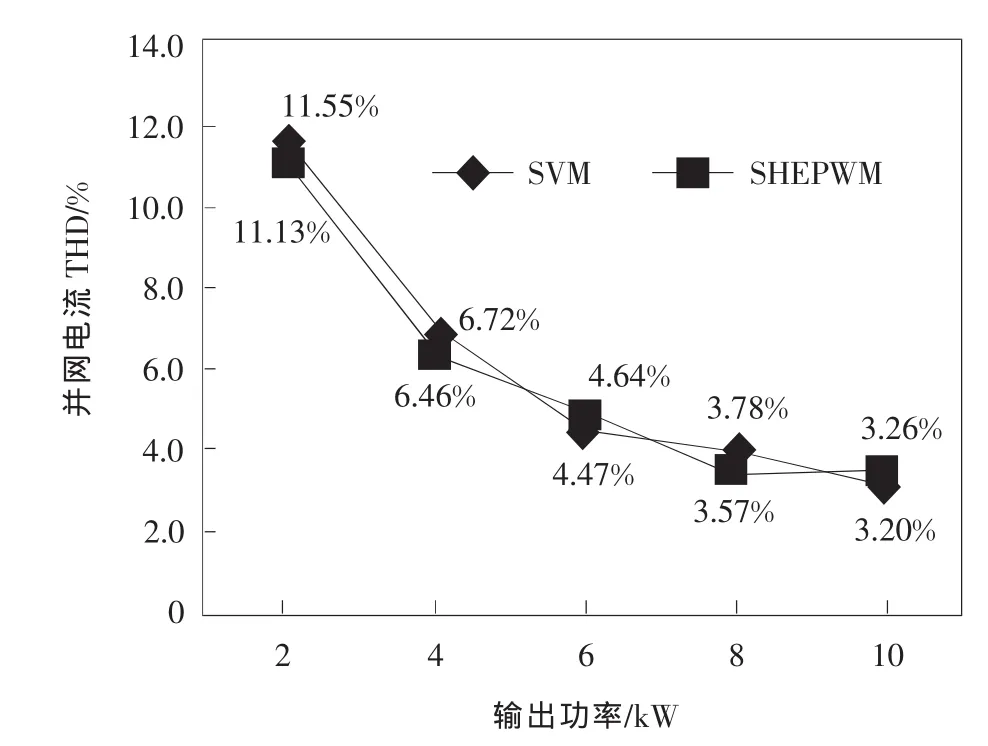
图16 实验并网电流THD

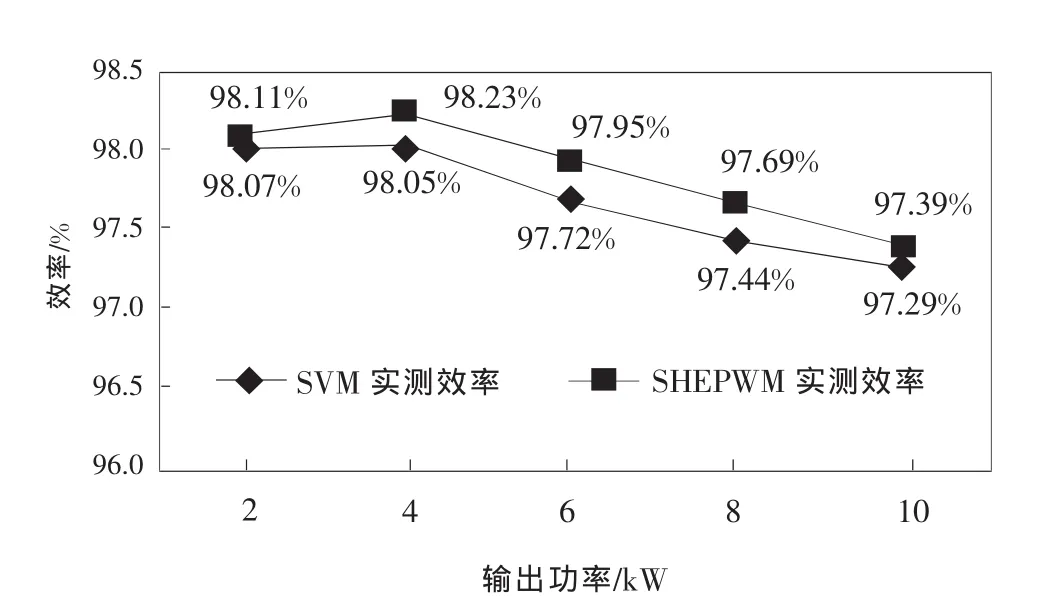
图17 实验效率

两种调制方式在不同功率等级并网时的效率曲线如图17所示。采用WT1800功率分析仪进行测量。由于SHEPWM中电网电压谐波引入的低次电流谐波，以及线缆损耗等的存在，导致SHEPWM的实测效率会略低理论效率。由图可知，SHEPWM最高效率为98.23%，满载效率97.39%，而SVPWM最高效率为98.07%，满载效率为97.29%。由于SHEPWM开关损耗的减小，其效率会比SVPWM有一定的提升。

6 结语

本文探讨了应用特定谐波消除法（SHEPWM）的T型三电平并网逆变器。首先对开关角个数进行了选择和求解，再对电流环路进行了分析和设计。之后，通过比较SHEPWM和SVPWM两种调制方式对逆变器的并网电流畸变率（THD）及损耗影响，指出由于SHEPWM可以消除特定的低次谐波，使得逆变输出电压的低次谐波大大减小，从而降低了并网电流的THD。同时，由于降低了等效开关频率，使得SHEPWM具有比SVPWM更低的损耗和更高的效率。此外，由于电网电压谐波的存在，使得SHEPWM的并网电流中也会出现和电网电压一致的低次谐波，一定程度地降低并网电能的质量和整机效率，但其总体效率还是略高于SVPWM。实验结果也验证了该结论。

［1］Grahame H D,Lipo T A,周克亮.电力电子变换器PWM技术原理与实践［M］.北京:人民邮电出版社,2010.

［2］ Patel H S,Hoft R G.Generalized technique of harmonic elimination and voltage control in thyristor inverter:part I-harmonic elimination［J］.IEEE Trans on Industry Application,1973,9（3）:310-317.

［3］ Wang Yongxing,Wen Xuhui,Guo Xinhua,et al.Vector control of induction motor based on selective harmonic elimination PWM in medium voltage high power propulsion system［C］//In Electric Information and Control Engineering（ICEICE）.2011:6351-6354.

［4］ Kavousi A,Farokhnia N,Fathi S H,et al.Implementation of Selective Harmonic Elimination PWM switching strategy on DSTATCOM［C］//Electrical Power Quality and Utilisation （EPQU）.2011:1-6.

［5］ Zhao Zhengmi ng,Zhong Yulin,Gao Hong wei,et al.Hybrid selective harmonic elimination PWM for commonmode voltage reduction in three-level neutral-pointclamped inverters for variable speed induction drives［J］.IEEE Trans on Power Electronics,2012,27（3）:1152-1158.

［6］ Dahidah M S A,Agelidis V G.Selective harmonic elimination PWM control for cascaded multilevel voltage source converters:A general ized formula ［J］.IEEE Trans on Power Electronics,2008,23（4）:1620-1630.

［7］张永昌,赵争鸣.三电平逆变器SHEPWM多组解计算方法［J］.电工技术学报 2007,22（1）:74-78.

［8］全国太阳光伏能源系统标准化技术委员会.GB/T 19939—2005光伏系统并网技术要求［S］.北京：中国标准出版社，2005.

［9］刘文华，宋强，陈远华,等.NPC逆变器SHEPWM开关角度的计算方法研究［J］.中国电机工程学报,2002,22（11）：31-34.

［10］张俊.基于间歇性双边无功功率扰动的三相并网逆变器孤岛检测研究［D］.杭州：浙江大学,2011.

［11］徐德鸿.电力电子系统建模及控制 ［M］.北京:机械工业出版社,2007.

［12］孙超.三电平T型并网逆变系统设计［D］.杭州：浙江大学，2013.