基于模糊PI并联控制永磁同步电机转动惯量问题研究

张晓光，柳同升，刑旭东

（1.天津大学电气与自动化工程学院，天津300072；2.天津奧特控制设备有限公司，天津300350）

引言

当今社会的生活和生产都离不开电梯，对电梯的控制要求也越来越高。永磁同步电动机具有体积小、转矩大、低速性能好等优点，在电梯门机控制系统中的应用越来越广泛，在采用永磁同步电机直驱的电梯门机控制系统中，永磁同步电机工作在频繁开关门状态，由于厅门本身的重量，使得电机在带动厅门和不带动厅门的情况下系统折算到电机轴的转动惯量有很大差别；除此之外，为了保障安全，电梯厅门会安装厅门自闭系统，当轿厢在开锁区域以外时，厅门无论因何种原因开启，这种装置都会利用重锤或弹簧来实现厅门强迫关闭。由于厅门自闭装置的存在，使电梯门机系统在开门和关门过程中进入开锁区域时折算到电机转轴上的转动惯量差别也很大,易造成电梯门反映迟钝、噪音和震动等问题，也容易引起系统内大电流冲击，这是到目前为止电梯所普遍存在的问题［1］。

针对转动惯量变化这一问题，一些专家学者通过不同的方法对转动惯量进行辨识［2-3］，辨识方法大多是基于电机数学模型，模型精确程度会影响辨识结果，同时转动惯量辨识存在辨识实时性、辨识精确性和实现算法复杂性等问题。相比较而言，模糊控制不依赖被控对象的精确数学模型,有较强的鲁棒性,但在控制精确度要求较高的场合,其稳态精确度不能令人满意。经典PID控制是一种线性方法，控制算法简单，积分作用可以消除稳态误差。因此把模糊控制和PID相结合的控制算法［5-6］便应运而生。

电梯门机系统针对转动惯量变化问题，可以采用两组PI分别对应有厅门和无厅门的过程，但两组参数以及两组参数在开关门过程中切换的具体位置需要根据门机系统分别进行人工调试。为改善电梯门机系统对转动惯量的适应能力和鲁棒性能，本文基于Matlab建立了控制系统的仿真模型,并在该模型基础上进行了模糊PI并联控制方法的仿真实验,在仿真的基础之上，基于HAD-YCBⅢ变频器进行工程验证,仿真结果和工程应用证明，这种模糊PI并联控制方法能够有效的抑制转动惯量变化对系统造成的影响，提高系统的动态性能，同时兼有经典PID控制的稳定性，并使系统具有一定的适应能力。

1 PMSM模糊PI并联矢量控制

1.1 PMSM机械系统动态模型

永磁同步电机机械系统动态模型如图1所示。

图1 永磁同步电机机械系统动态模型

系统的机械运动方程为

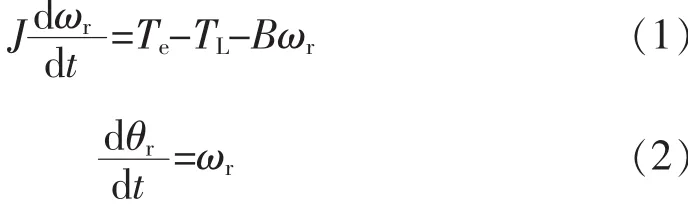
式中：Te、TL分别为电磁转矩和负载转矩；θr为转子位置电角度；ωr为转子机械角速度；J为转动惯量；B为阻尼系数。

1.2 PMSM总体控制方案

常规的PMSM调速控制系统多采用转速控制与转矩控制双闭环级联结构,通过Clarke变换和Park变换将电机变量从静止abc坐标系变换到转子旋转dq坐标系，通过控制id和iq实现对电磁转矩的控制，其中比较常用的一种控制策略是id=0控制策略。为了克服转动惯量大范围变化造成的影响，本文在常规控制策略基础上,构造模糊PI并联控制器，其系统框图如图2所示。

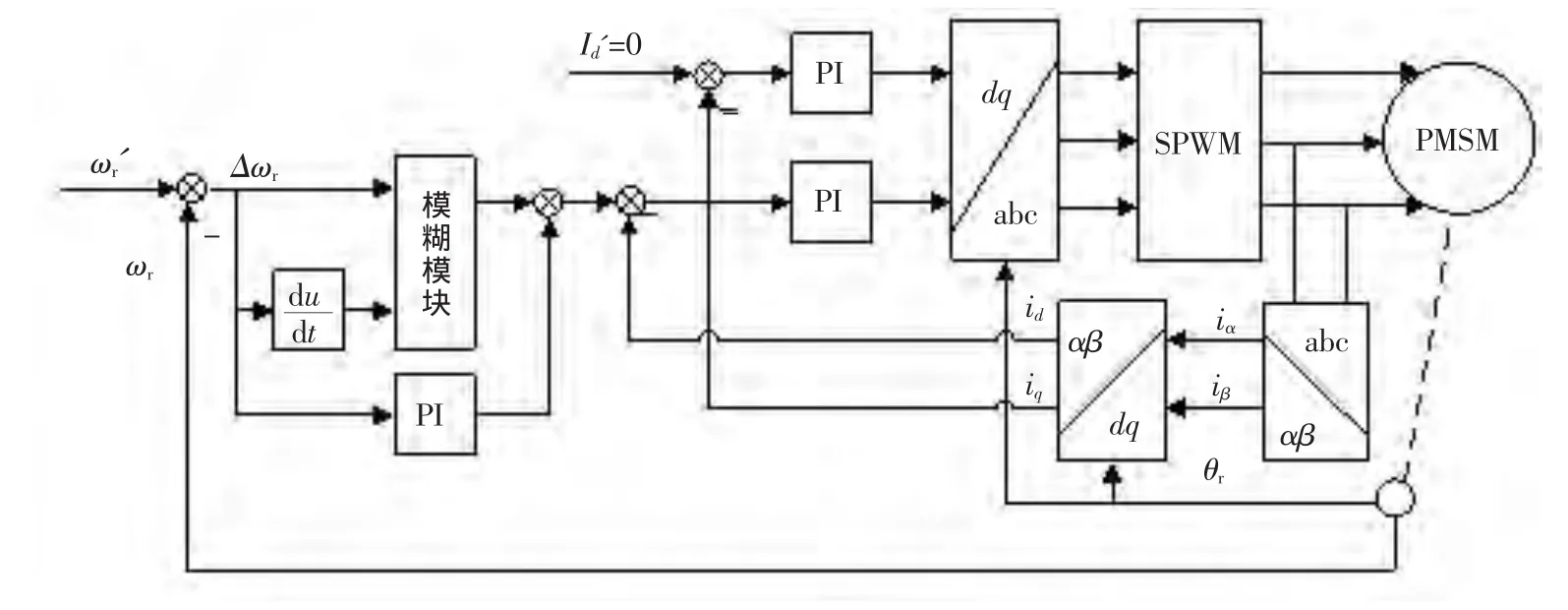
图2 永磁同步电动机矢量控制的双闭环模糊PI并联控制系统框图

1.3 模糊控制策略的实现

模糊控制器由模糊化、模糊规则、模糊推理和清晰化 4 部分组成［7］。

模糊化的任务是将清晰量转换为模糊控制器可以接受的模糊量，模糊控制器有2个输入变量：转速误差e和转速误差变化率ec。模糊控制器输出变量为u。定义e对应的模糊变量为EF，其模糊子集为 EF=｛NB,NM,NS,ZE,PS,PM,PB｝，ec对应的模糊变量为CEF，其模糊子集为CEF=｛NB,NM,NS,ZE,PS,PM,PB｝，模糊输出变量为UF，其模糊子集为UF=｛NB,NM,NS,ZE,PS,PM,PB｝。模糊输入变量的隶属度函数如图3（a）所示，模糊输出变量的隶属度函数如图3（b）所示。隶属度函数采用变模糊集宽度设计方案，在误差较小的区域提高模糊集分档密度，以在不增加模糊集个数前提下提高控制精确度。

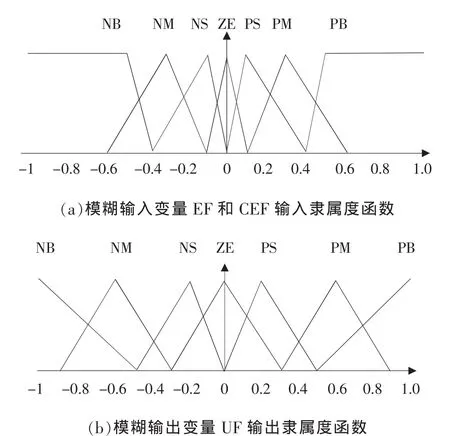
图3 模糊输入和输出的隶属度函数

模糊规则是设计模糊控制器的核心。转速误差较大时，重点考虑系统的快速性，应使输出量增大，使电机产生的电磁转矩大，从而获得大的加速度，使电机转速尽快地向给定转速变化。当转速误差较小且达到一定范围时，重点考虑系统将要出现的超调，该阶段应突出误差变化率ec的控制，以达到提前调节的作用，同时将调节量细化，提高控制量的精确度。当实际转速与给定速度的误差接近零时，需要考虑系统的稳态性能，在保证小的稳态误差同时加强抗干扰调节，此时应该根据e和ec的细微变化，迅速调节控制量。

转动惯量变大时调节时间延长，此时偏差较大，偏差变化率则相对较小，体现在表1中虚线框部分，应当加大控制量的输出，提高系统的响应速度，使转速尽快跟踪给定速度；转动惯量变小时振荡严重，此时突出特点是误差变化率较大，偏差呈现周期性变化，体现在表1中双实线框部分，应当尽量减小控制量的输出，防止大超调和剧烈振荡的出现。

依据以上设计原则和参数设计应尽可能平滑的原则，结合仿真实验设计模糊控制规则见表1。

糊推理采用 Mamdani的 Min-Max 方法［7］，模糊推理的输出曲面如图4所示。

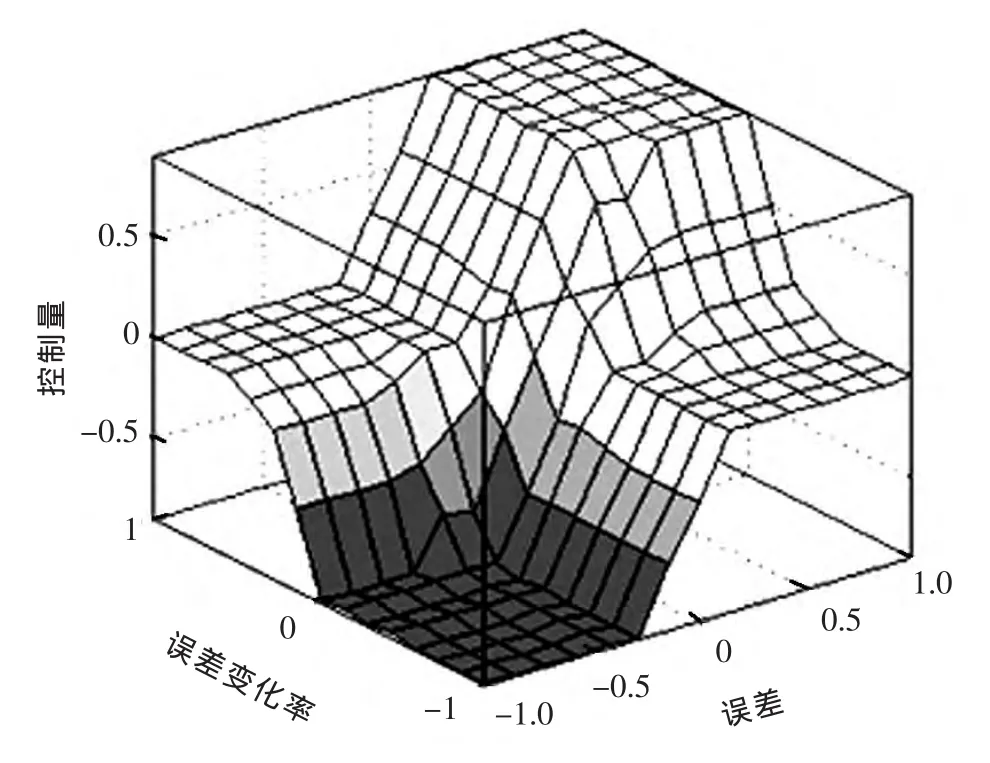
图4 模糊推理的输出曲面

清晰化：模糊控制器输出的控制量UF是一个模糊子集，反映控制变量不同取值的一种组合方式，需要通过模糊控制器的清晰化过程得到精确控制量。本文中清晰化方法采用重心法。重心法的输出较其他清晰化方法更加平滑，可以使控制系统获得更好的稳态性能。

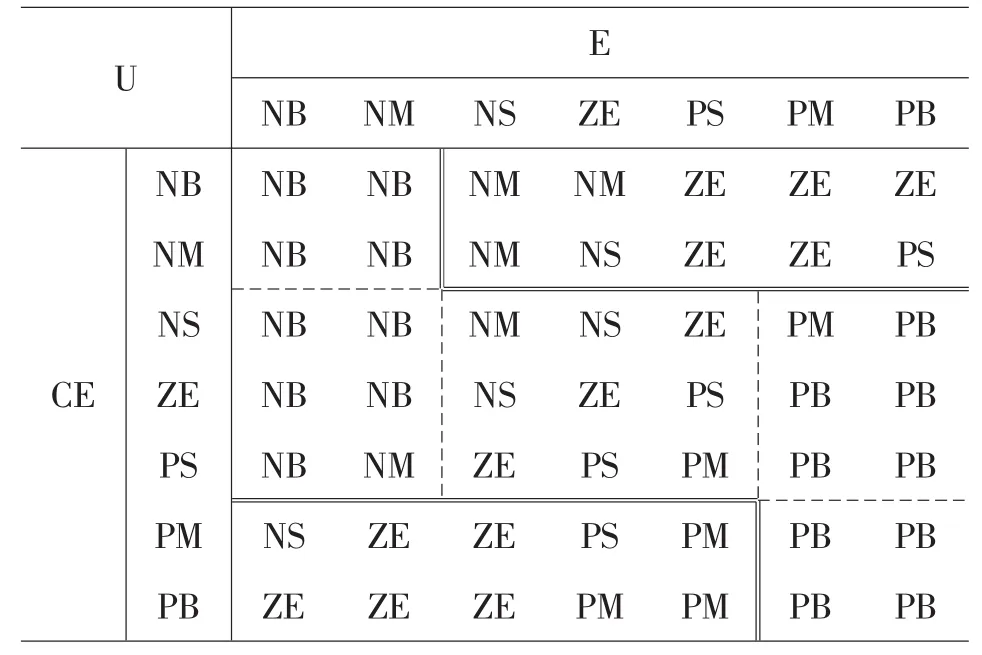
表1 模糊规则控制表

2 控制系统仿真结果及分析

为验证本文所提出的控制方法，应用Matlab/SIMULINK工具对控制系统建模并进行仿真研究。仿真模型如图5所示，主要由模糊控制模块、电流PI控制模块、变换模块、PMSM模块等子系统组成。

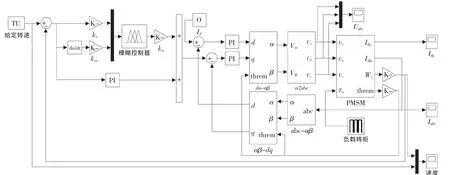
图5 模糊PI并联控制仿真模型

其中永磁同步电机的仿真模型参数选择如下：定子电阻Rs=105 Ω，直轴电感、交轴电感Ld=Lq=0.032 H，永磁体磁链 φf=0.7 Wb，额定转矩 Te=3 N·m，极对数pn=26。为了验证所设计的模糊PI并联控制能够提高门机控制器的控制性能，进行如下仿真测试。

2.1 转速跟踪响应

PI 参数采用 J=0.1 kg·m2的最佳固定 PI［1］，PI控制器采用工程设计方法，电流内环以跟随为主，选用典型Ⅰ型系统，速度外环以抗扰动性能为主，选用典型Ⅱ型系统［8］。模糊PI并联控制器由上文设计方法得到。保持其他参数不变的情况下，改变转动惯量，在J=0.1 kg·m2的基础上分别缩小和放大10倍。其仿真结果如图6所示。

其转动惯量分别为 J=0.01 kg·m2、J=0.1 kg·m2、J=1 kg·m2。系统阶跃输入跟随性能指标如表2所示。

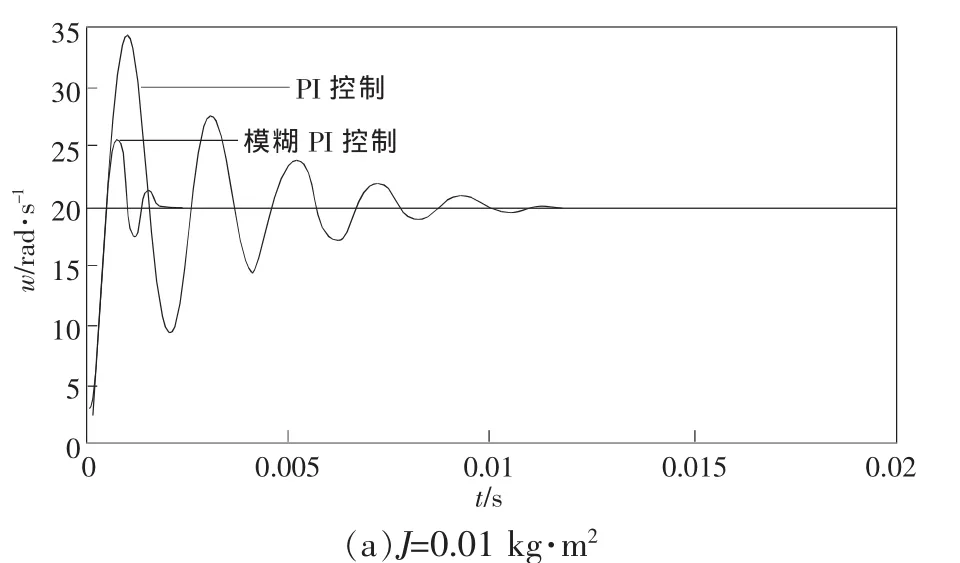
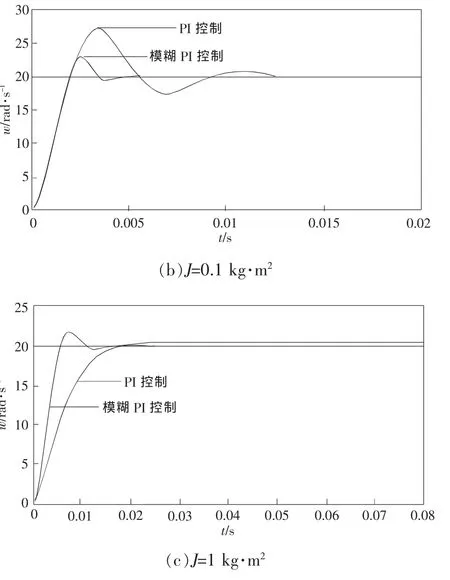
图6 不同转动惯量下系统阶跃响应曲线

由图6和表2分析可知，对于PI控制器当转动惯量缩小10倍时，系统振荡严重，而模糊PI并联控制并没有明显的振荡，同时模糊PI并联控制的超调明显小于PI控制，且PI控制器的调节时间是模糊PI并联控制器的6倍；对于PI控制器当转动惯量放大10倍时，系统反应明显迟钝，调节时间增大为原调节时间的30倍，而模糊PI并联控制器调节时间几乎没变。由以上分析可知，模糊PI并联控制可以有效的克服转动惯量变化对系统造成的影响。

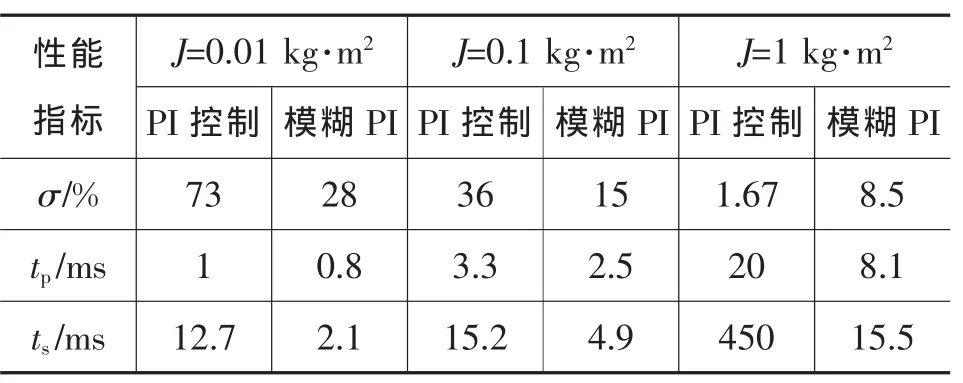
表2 阶跃输入跟随性能指标对比表

2.2 电梯门机运行曲线仿真结果

电梯门机系统不带厅门自闭装置时，转动惯量变化曲线如图 7（a）所示，仿真结果如图 7（b）和 7（c）所示。从电梯门机运行曲线仿真结果来看，模糊PI并联控制结合了模糊控制和PI控制的优点，提高动态性能的同时，也可以满足稳态的无差性。

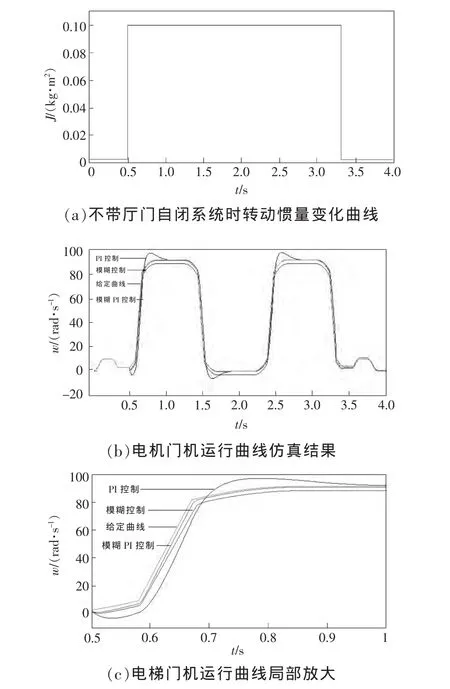
图7 不带厅门时转动惯量变化曲线和电梯门机运行仿真曲线

电梯门机系统带厅门自闭装置时，转动惯量变化曲线如图 8（a）所示，仿真结果如图 8（b）和 8（c）所示。从电梯门机运行曲线仿真结果来看，模糊控制由于误差太大无法满足控制要求，模糊PI并联控制能够很好地满足控制要求。

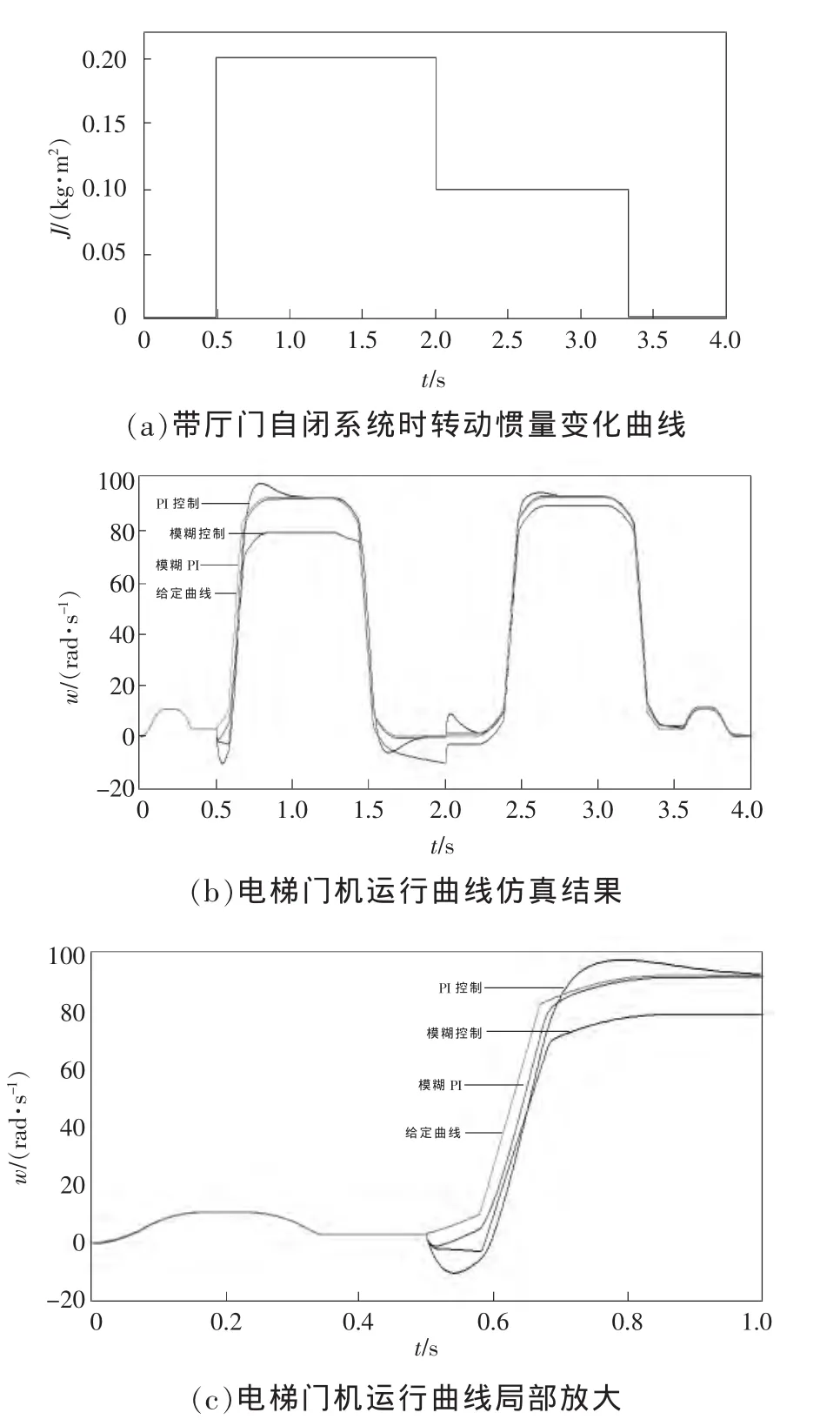
图8 带厅门时转动惯量变化曲线和电梯门机运行仿真曲线

2.3 工程验证

基于HAD-YCBⅢ变频器编写模糊控制程序和模糊PI并联控制程序，轻门实验采用不带厅门且轿门只有实际轿门一半重量的实验门来进行实验；重门实验采用带有厅门和厅门自闭装置的真实电梯门进行实验。两者重量相差在10倍以上。

轻门实验的实验结果如图 9（a）～（c）所示，其中图9（a）为PI控制，PI参数选用电机空载时参数，从实验现象和运行曲线来看，门机动态过程迟滞，可以完成开关门动作，但带门前后，由于转动惯量的变化，门机无法快速跟踪给定曲线；图9（b）为模糊控制，可以完成开关门动作，但从运行曲线来看运行过程中误差明显；图9（c）为模糊PI并联控制，动态性能良好，开关门过程高速平滑，其控制性能明显优于PI控制和模糊控制。

重门实验的实验结果如图 9（d）～（e）所示,其中图9（d）为PI控制，由于带有厅门自闭装置，电梯开门转动惯量明显大于关门转动惯量，从开关门运行状态来看，可以完成电梯的开关门动作，但开门过程快速性明显劣于关门过程，从运行曲线来看，开门过程和关门过程存在明显差别，开门过程由于转动惯量较大，无法快速跟踪给定曲线，存在明显的滞后和超调，而关门过程则高速平滑，由此可见当存在厅门自闭系统时，PI控制无法同时满足开门过程和关门过程运行的高效性；模糊控制由于存在较大的误差不能满足控制要求；图9（f）为模糊PI并联控制，从开关门运行状态来看，可以高速平滑的完成开关门动作，从运行曲线来看，开门过程无明显的滞后和超调，其动态性能明显优于PI控制。除此之外，工程实际应用证明模糊PI并联控制的参数更容易调节，且参数具有一定的适应能力。

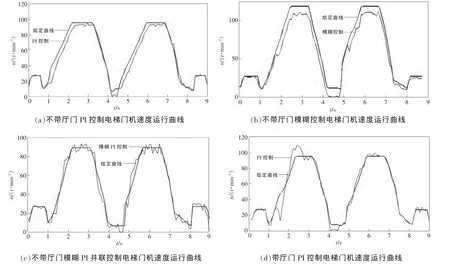
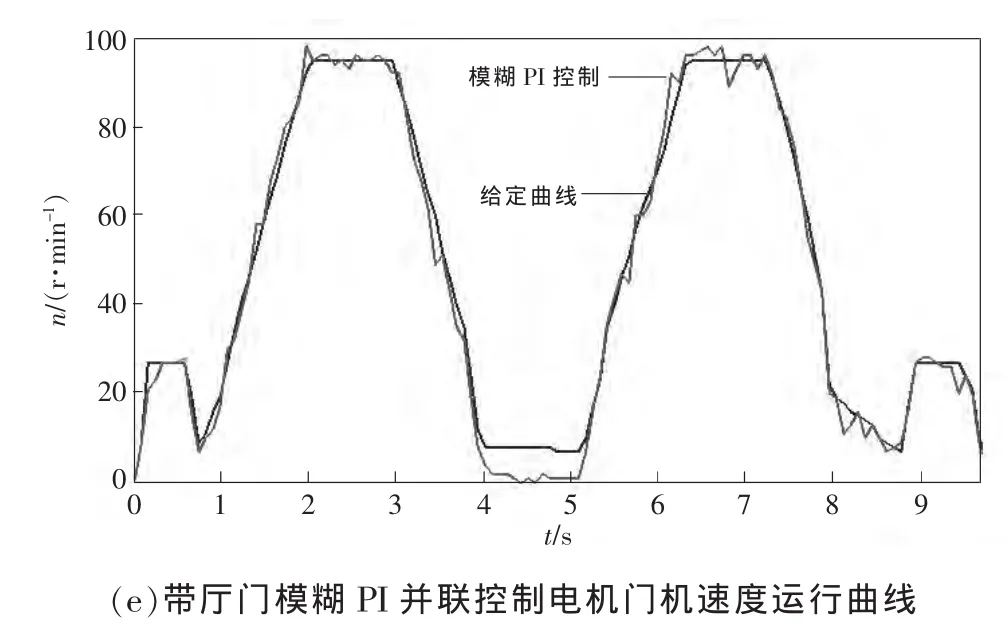
图9 不同控制算法的工程实验结果

3 结语

本文从工程实际出发，针对电梯门机系统中永磁同步电机转动惯量大范围变化导致控制效果变差这一现象，设计了模糊PI并联控制器。仿真结果和工程实验结果均证实，这种控制策略可以提高系统的动态性能，有效抑制系统转动惯量大范围变化对门机系统动态性能的影响，缩短系统参数调节时间，使系统具有一定的适应能力。

［1］王鑫，韩洪洪.模糊PI控制在电梯门机系统中的应用［J］.天津理工大学学报，2012，28（4/5）：37-40.

［2］ Du Shuai,Zhao Shouhua,Chen Yangsheng.Inertia identification for speed control of PMSM servo motor［C］//2011 Internatinal Conference on Electrical Machines and Systems（ICEMS）.Beijing,China 2011:1-6.

［3］ Zhao Shouhua,Cui Lin,Liu Guiying,et al.An improved torque feed-forward control with observer-based inertia identification in PMSM Drives［C］//15th International Conference on Electrical Mechines and Systems.Sapporo,2012:1-6.

［4］ Cao Xianqing,Bi Meng.Extended luenberger observer based on dynamic neural network for inertia identification in PMSM servo system［C］//Fifth International Conference on Natural Computation.Tianjin,China,2009:48-52.

［5］王迪,王旭东.引入智能积分器的PMSM模糊控制系统［J］.电机与控制学报,2014，14（10）：100-106.

［6］ Jung J-W,Cho Y-S,Leu V Q,et al.PI-type current controllers for permanent magnet synchronous motors［J］.IET Electri Power Appl， 2010,5（1）:143-152.

［7］易继锴，侯媛彬.智能控制技术［M］.北京：北京工业大学出版社，2007.

［8］陈伯时.电力拖动自动控制系统［M］.北京：机械工业出版社，2003.