地表温度的被动微波遥感反演研究进展

周芳成，宋小宁，李召良

(1.中国科学院大学资源与环境学院，北京 100049;2.中国农业科学院农业资源与农业区划研究所农业部农业信息技术重点实验室，北京 100081;3.法国斯特拉斯堡大学ICube实验室，斯特拉斯堡 67412)

0 引言

地表温度(land surface temperature，LST)是地表能量平衡中一个重要的参数，影响着土壤和植被的蒸散作用、作物产能、区域水热交换和土壤微生物生化指标等众多领域;LST也广泛应用在检测森林火灾、判别地热位置、寻找石油和铀矿等方面。遥感是快速获取大区域地表温度的最有效方法，基于热红外遥感的地表温度反演算法经过多年的发展已经趋于成熟，并已达到较高的精度[1-9]。但是热红外遥感受大气中水汽影响较大，不能穿透云层，无法全天候监测;而微波遥感穿透力强，能够弥补热红外的不足，发展基于被动微波遥感的地表温度反演算法已成为研究热点。被动微波遥感具有高时间分辨率且能迅速覆盖全球，为全球尺度的地表温度空间异质性及变化趋势的研究提供方便。

目前常用的星载微波辐射计主要有扫描式多通道微波辐射计(scanning multichannel microwave radiometer，SMMR)、微波辐射计特别传感器(special sensor microwave imager，SSM/I)、高级微波扫描辐射计(advanced microwave scanning radiometer-EOS，AMSR-E)。相关研究已较多，但是与热红外遥感相比，微波遥感反演地表温度尚处于起步阶段，仍然面临着对微波穿透深度考虑不足、低频微波的无线电频干扰、地表温度与比辐射率的分离等诸多问题。本文通过梳理当前基于被动微波遥感的地表温度反演算法，将其大致分为统计模型法、物理模型法和神经网络算法3类，并分析各种方法的优缺点，确定下一步研究的切入点，为推动地表温度的被动微波遥感反演研究提供参考。

1 统计模型法

当微波辐射计的天线主波束指向目标时，天线接收到目标辐射、散射和传播介质辐射等能量，天线接收的信号经放大、滤波、检波和再放大后，以电压形式输出。对微波辐射计的输出电压进行温度绝对定标，即可建立输出电压与天线温度的关系，天线温度经过偏移校正和非线性校正等处理即可得到极化亮温数据。由此可知，微波辐射计获得的亮温数据与目标辐射之间有较好的相关关系，而目标辐射又主要受温度的影响，因此可以通过回归分析直接建立微波亮温数据与真实地表温度之间的相关关系。

1.1 单通道回归分析

Holmes等[10]利用37 GHz的垂直极化亮温数据建立了简单的地表温度反演模型，在全球尺度的验证时发现在高植被地区的偏差可以小于1 K，而在低植被区精度稍差。毛克彪等[11]将同步的MODIS地表温度产品作为AMSR-E对应的地面实测数据，将MODIS温度产品和AMSR-E的6种频率的V极化亮温分别进行回归分析，发现随着频率的升高，相关性越来越好(表1)。原因在于高频通道的辐射主要来自较浅的地表发射层，与热红外探测的温度更加接近;而低频通道由于具有较好的穿透性，其发射层可能是一定深度土壤，得到的亮温是体积亮温而非表面亮温，因此存在较大误差。

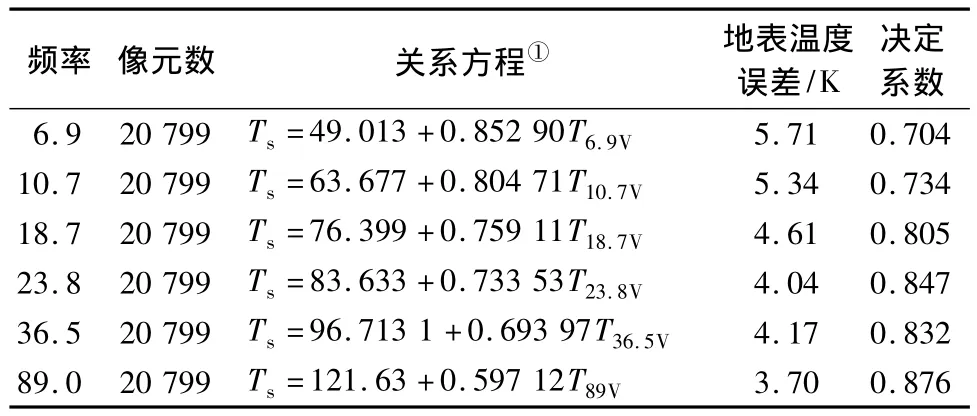
表1 MODIS温度产品和AMSR－E亮温的关系[11]Tab.1 Relationship of MODIS LSTs and AMSR－E brightness temperature data[11]

1.2 多通道回归分析

McFarland等[12]首先剔除了研究区内水体和雪等像元点，将SSM/I所有7个通道亮温数据与研究区内百叶箱最低空气温度(代表地表温度)进行多元回归分析，建立了以SSM/I 37 GHz垂直极化亮温为主因子、利用其他通道进行水汽影响校正的4通道地表温度反演算法，即

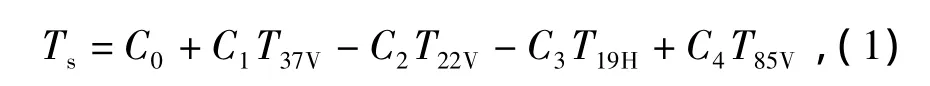
式中:Cn为回归系数(n=1，2，3，4);TxV和 TxH分别代表频率为x GHz的V和H极化亮温(x=19，22，37，85)，K。

对美国中部平原3种下垫面条件(农作物、湿润的土壤以及干土)的地表温度进行反演，所得结果与百叶箱温度较为一致，其均方根误差(root mean square error，RMSE)值为 2.0 ～ 2.6。Holliger[13]基于McFarland算法的基本原理，使用包括不同季节和夜间的数据参与回归分析，发展了SSM/I每日地表温度产品的算法。毛克彪等[14]针对AMSR-E传感器的频率特点将式(1)中V和H的极化亮温分别改为 T36.5V，T23.8V，T18.7H和 T89V，应用到中国东北(森林)、非洲北部(荒漠)和中国西藏(冰雪)地区，并且用同期的MODIS地表温度产品作为真实值进行验证，取得了较满意的结果。

1.3 基于地表覆被分类的多通道回归分析

武胜利等[15]利用MODIS的陆表分类产品(MOD12)将陆表分成16类，假设每种类型地表在各个被动微波通道具有一致的比辐射率;陈修治等[16]以广东省为研究对象，依据微波极化差异指数、归一化植被指数和比值植被指数等3种植被指数，将广东省地表植被覆被情况分为裸地、草地、灌木、针叶林和阔叶林等5种类型。在地表覆被分类的基础上，分别建立了不同覆被类型的地表温度反演模型，取得了较好的精度。

总体来看，统计模型是通过分析大量数据，利用较简练的回归模型表征亮温与地表温度之间的内在关系，具有一定的物理意义;而且该方法适合于多数地表覆被类型，使用灵活;方法简单易懂，可以作为一种快速获取地表温度的途径。但是各通道系数的确定只通过回归算法求出，缺乏物理依据，不同时间、不同地区的系数可能不同，每次应用都需要重新确定参数，降低了应用效率;并且模型的精度很大程度上依赖数据本身的质量，具有较大的不确定性。

2 物理模型法

2.1 微波辐射传输方程

地球系统的能量守恒是遥感探测地表参数的理论基础。根据普朗克辐射定律，黑体在所有方向上均匀辐射，其谱亮度为

其在微波波段的近似式是瑞利—琼斯定律，如hf/kT远远小于1，式(2)可简化为

式中:Bf(T)是谱亮度，W·m-2·sr-1·Hz-1;f是频率，Hz;T是绝对温度，K;λ为波长，m;h是普朗克常数6.63 ×10-34;k 是波尔兹曼常数 1.38 ×10-23J·K-1;c是光速。

裸土情况下，地表温度反演的微波辐射传输方程通常由3部分组成:①大气上行辐射;②经大气衰减的表面辐射;③经表面反射和大气衰减的大气下行和宇宙辐射。模型表示为

将式(3)代入(4)得

式中:TB指频率为f Hz的亮温值，K;Ts为地表温度，K;Ta为平均空气温度，K;Tsky为宇宙背景辐射亮温，K;Bf(Ts)为地表辐射，W·m-·2sr-·1Hz-1;Bf()和 Bf)分别指大气下行辐射和大气上行辐射，W·m-·2sr-·1Hz-1;τf(θ)指频率为f的大气透过率;ef指地表比辐射率，无量纲。

对于土壤-植被表面，通常将植被看作粗糙土壤上的一种单散射层，在大气顶部观测得到的辐射由5部分组成:①大气上行辐射;②经植被和大气衰减的土壤表面辐射;③经大气衰减的植被上行辐射;④经表面反射并被植被和大气衰减的植被下行辐射;⑤经林冠和大气衰减的表面反射的大气下行和宇宙辐射。辐射传输方程为

将式(3)代入(6)得

式中:Bf(Tc)是植被辐射，W·m-2·sr-1·Hz-1;w是植被单向散射反照率;τc(θ)是植被透过率，无量纲。

通过式(5)(7)可以看出，地表温度与大气、植被、亮温和比辐射率有关。对于大多数气象条件，若频率低于10 GHz，可以不考虑散射效应[17];当波长足够长时，地面微波辐射可以穿透植被层进入到微波辐射计，因此，公式中主要的未知数仅剩下比辐射率。与热红外不同，微波比辐射率随土壤含水量的不同变化较大[18]，这使得热红外反演地表温度中对比辐射率的假设不能被完全照搬到微波中，因此方程中未知数的个数大于方程数，即使增加通道，但问题依然存在，属于典型的病态反演问题。针对这一问题，学者们提出了多种解决办法。

2.2 基于比辐射率求解的反演方法

Gao等[19]假设地表温度与亮温和比辐射率呈简单的线性关系，通过陆表微波比辐射率模型(land surface microwave emissivity model，LSMEM)模拟了亚马逊高植被区和低植被区比辐射率和极化比的关系(极化比被定义为同频率下的水平亮温与垂直亮温之比)。研究发现，对高植被区，18.7 GHz的比辐射率是18.7 GHz极化比的二次函数(式8);对低植被区，18.7 GHz的比辐射率是 6.9 GHz和 18.7 GHz极化比的二元函数(式9)，即

式中:e18，f和 e18，nf分别为高、低植被区 18.7 GHz 的比辐射率;PR6和PR18分别为6.9 GHz和18.7 GHz的极化比，无量纲。可先由式(8)(9)求出比辐射率，再根据假设，结合亮温求出地表温度。

除了上述方法，学者们还尝试构建一些对比辐射率敏感而对地表温度和大气不敏感的指数来建立与比辐射率的经验关系，求解比辐射率并进一步求解地表温度，如归一化植被指数[20]、归一化极化指数[21]、组合亮温指数[22]等。

该温度反演方法是通过直接求解比辐射率来解决病态反演的问题，对地表温度、大气情况的依赖性小，所需数据简单易得，能取得较好的精度;但是对比辐射率的求解仍是一种经验回归方法，仍存在物理机制不强的缺憾。

2.3 基于比辐射率不变假设的反演算法

2.3.1 基于两邻近通道的反演算法

Weng等[23]假定 SSM/I的2 个邻近通道(19.35 GHz，22.23 GHz)V极化的比辐射率相等，2个通道亮温的差异主要来自大气的影响。在式(5)的基础上假定大气上行和下行辐射相等，并忽略宇宙辐射的影响，引入总可降水量这一新参数，通过比值的形式建立了反演地表温度的非线性方程，即

可使用牛顿迭代方法进行求解，式中:W为总可降水量;A 为依赖于频率的常数，A19=0.047，A22=0.136;β(W)与2个频率的大气透过率有关;TxV代表频率为x GHz的 V极化亮温(x=19，22)，K。

该温度反演方法通过2个邻近通道消除比辐射率的影响，不需要地表分类。但是微波与热红外不同，不同频率间比辐射率差异较大(图1)。

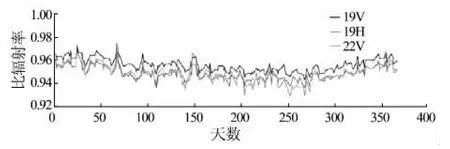
图1 比辐射率日变化曲线[24]Fig.1 Curve of diurnal variation of emissivity[24]

根据文献[25]，0.006～0.012 的比辐射率误差将导致大约3 K的地表温度波动，因此该方法关于相邻通道比辐射率相等的前提假设可能会带来较大的误差。

2.3.2 基于多时相的反演算法

Pulliainen等[26]假定同一点的比辐射率不随时间变化，利用长时期多时相的SSM/I数据，采用最大似然法估算表面平均比辐射率，并用最小二乘迭代法求得平均比辐射率;将大气看作是已知平均值和标准差的一种自由参数或者Gaussian随机变量，采用强迫最小二乘迭代法估算地表温度Ts，即

式中:min为最小二乘法中取最小值;σi为获取的SSM/I通道i的亮温标准差(由SSM/I的灵敏性特征决定);λ为常数值γ的标准偏差;γ^为γ的平均值;Tbi为SSM/I通道i观测亮温，K;TBi为辐射传输模型模拟通道i亮温值，K。该方法适用于无雪条件，水体或农业用地比例的增加会使误差增大。

Xiang等[27]假定同一频率的比辐射率在1 d之内不发生变化，使用多通道每天2次(升轨和降轨)的SSM/I亮温数据和大气的温湿度廓线数据作为输入，发展了一种不依赖地表介电的反演地表温度和比辐射率的方法，分别设置地表温度和比辐射率的允许范围分别为280～340 K 和0.70～1.00，并采用最小二乘Levenberg-Marquardt迭代算法对非线性方程求解。

该温度反演方法通过假设比辐射率不随时间变化来解决未知数大于方程个数的问题，但是根据前人的研究证明，通常地表温度最高时比辐射率也最高，地表温度低时比辐射率也较低，因此该前提假设并不符合实际[28-32]，会带来较大的误差。

2.4 基于极化比辐射率关系的反演算法

Fily等[30]通过SSM/I数据获得的全球陆地比辐射率发现19 GHz和37 GHz的垂直和水平极化比辐射率呈非常显著的线性相关关系，设eH=aeV+b，并且忽略宇宙辐射，由式(5)得出简化的地表温度的反演算法，即

式中:T19H和T37H分别是19 GHz和37 GHz通道的水平或者垂直极化的亮温，K;a和b为比辐射率线性方程中的斜率和截距，无量纲;τ为大气透过率;Tau和Tad分别为大气上行与下行辐射亮温，K。

该温度反演方法通常使用物理模型拟合出不同频率的垂直(V)和水平(H)极化比辐射率的相关关系，然后可通过辐射模型中的大气模块估算 Tau，Tad，τ等大气参数，适用于无冰雪、无冰冻地面。该算法简单易行，误差主要来源于比辐射率线性关系的拟合和大气校正带来的误差。

3 神经网络算法

神经网络算法不需要针对具体的问题推导计算规则，而只需要利用有代表性的训练数据集进行训练学习[31]，可以并行地求解非线性问题而不受方程自身的约束，因此被认为是解决病态反演问题的有效方法。很多学者将其应用到地表温度的被动微波反演中:Zurk等[32]利用多层感知器(multilayer perceptron，MLP)神经网络方法，先在合理范围内改变土壤含水量、植被含水量和土壤温度等，生成地表温度范围，再用后向传播算法反演地表温度，精度达到2 K;毛克彪等[31]利用神经网络算法，通过AMSR-E的多通道亮温数据反演地表温度，并发现当使用5个频率10个通道反演时，反演精度最高。

该温度反演方法利用了参数之间的固有关系，通过神经网络算法的特点解决了地表参数之间的非线性问题。但是该算法只是在数学层面弱化了病态反演的问题而缺乏实际物理意义，并且需要先验知识(考虑各种情况的数据库)作为支撑，有关该方法的应用还需进一步研究。

4 结论与展望

微波遥感与可见光、红外遥感一样已成为人类探测地球信息的一种非常重要的手段，虽然起步较晚，但是凭借其受大气干扰小、能穿透云层甚至一定程度的雨区等优点，弥补了可见光和红外遥感的不足，能做到全天候观测，应用领域广泛。微波遥感反演地表温度大致可分为统计模型法、物理模型法和神经网络算法3种。

统计模型法利用亮温与地表温度之间的内在关系，通过大量数据回归总结规律，算法的机理简单，便于实现。但是统计模型中的常数项不具备物理意义，随地域和时间的改变而改变，具有很大的局限性;并且模型的精度很大程度上依赖于数据本身质量，有较大不确定性。物理模型法基于辐射传输方程，将视在亮温分为目标亮温和其他辐射贡献2部分，剔除其他辐射贡献以及通过目标亮温得到目标真实温度是反演的2个主要步骤。物理模型法具有明确的物理意义，不受时空的限制。但是模型中很多参数的机理尚不明确，在使用过程中大多通过条件假设进行简化，如采用常数进行大气校正、忽略宇宙辐射影响、用空气温度代替地表温度等，这些假设虽然降低了反演难度，但是无疑影响了反演精度。神经网络算法对数学方程依赖小，能较好地解决病态反演问题，但是该方法的物理意义不足，仍需进一步的研究。

通过对当前微波反演地表温度算法的总结，除了加强微波辐射机理的研究[28，33]，在今后的研究工作中还需注意以下3点:

1)微波穿透深度。热红外获得的主要是地表信息，微波由于波长较长，可以获得一定深度土壤信息，特别是低频通道，穿透深度不能被忽略，微波穿透深度与波长、土壤介电常数、入射角有关[34]。视在温度包含的目标亮温实际是土壤体积亮温而非表面亮温，因此，首先应了解微波的穿透深度，再寻找从体积温度推求地表温度的方法。对于某一传感器而言，波长和入射角都已固定，穿透深度只与土壤介电常数有关，而介电常数主要受土壤含水量影响，依托DOBSON模型可以由土壤含水量求取介电常数。微波对于土壤含水量具有高度敏感性，针对这一特点发展基于微波的地表温度与土壤含水量联合反演是未来的发展方向。

2)比辐射率模型。比辐射率是地表温度反演过程中一个关键参数，当前常用的比辐射率模型有物理模型和半经验模型2类。物理模型包括几何光学模型、物理光学模型、积分方程模型(integral equation model，IEM)和先进积分方程模型(advanced IEM，AIEM)。其中，AIEM模型精度较高，通过AIEM模型建立模拟数据库，探求各频率、各极化比辐射率之间的关系，可以以此来消除病态反演问题。

3)无线电频率干扰问题。近年来，由于无线电用户数目增多，无线电频率对微波遥感反演精度的干扰逐渐增加，对于低频微波的影响尤为严重，可能导致低频通道的亮温大于、甚至远远大于高频通道的亮温[35]，而低频通道由于具有良好的穿透力和对土壤水的高敏感性而常被用于反演地表参数，因此对受污染数据的识别和修正尤为重要，发展识别和修正RFI的算法也是未来研究的重点之一。

[1]徐希孺，柳钦火，陈家宜.遥感陆面温度[J].北京大学学报:自然科学版，1998，34(2/3):248-253.Xu X R，Liu Q H，Chen J Y.The remote sensing of land surface temperature[J].Acta Scientiarum Naturalium Universitatis Pekinensis，1998，34(2/3):248-253.

[2]Becker F，Li Z L.Temperature independent spectral indices in thermal infrared bands[J].Remote Sensing of Environment，1990，32:17-33.

[3]Caselles V，Coll C，Vator E.Land surface emissivity and temperature determination in the whole HAPEX-Sahel area from AVHRR data[J].International Journal of Remote Sensing，1997，18(5):1009-1027.

[4]Kerr Y H，Lagouarde J P，Inberon J.Accurate land surface temperature retrieval from AVHRR data with use of an improved split window algorithm[J].Remote Sensing of Environment，1992，41(2/3):197-209.

[5]Mcmillin L M.Estimation of sea surface temperatures from two infrared window measurements with different absorption[J].Journal of Geophysical Research，1975，80(36):5113-5117.

[6]Gillespie A，Rokugawa S，Maatsunaga T，et al.Temperature and emissivity separation algorithm for advanced spaceborne thermal emission and reflection(ASTER)image[J].IEEE Transactions on Geoscience and Remote Sensing，1998，36(4):1113-11126.

[7]Wan Z M，Dozier J.A generalized split-window algorithm for retrieving land-surface temperature from space[J].IEEE Transactions on Geoscience and Remote Sensing，1996，34(4):892-905.

[8]Wan Z M，Zhang Y L，Zhang Q C，et al.Validation of the landsurface temperature products retrieved from terra moderate resolution imaging spectroradiometer data[J].Remote Sensing of Environment，2002，83(1/2):163-180.

[9]Wan Z M，Zhang Y L，Zhang Q C，et al.Quality assessment and validation of the MODIS global land surface temperature[J].International Journal of Remote Sensing，2004，25(1):261-274.

[10]Holmes T R H，De Jeu R A M，Owe M，et al.Land surface temperature from Ka band(37 GHz)passive microwave observations[J].Journal of Geophysical Research，2009，114(D4):D04113.

[11]毛克彪，施建成，李召良，等.一个针对被动微波AMSR-E数据反演地表温度的物理统计算法[J].中国科学:D辑，2006，36(12):1170-1176.Mao K B，Shi J C，Li Z L，et al.A physical statistics algorithm for retrieval land surface temperature with passive microwave AMSRE data[J].Science China Earth Sciences，2006，36(12):1170-1176.

[12]McFarland M J，Miller R L，Neale C M U.Land surface temperature derived from the SSM/I passive microwave brightness temperatures[J].IEEE Transactions on Geoscience and Remote Sensing，1990，28(5):839-845.

[13]Holinger J P.DMSP special sensor microwave/imager calibration/validation，final report，vol.II[R].Washington:Naval Research Laboratory，1991.

[14]毛克彪，施建成，李召良，等.用被动微波AMSR数据反演地表温度及发射率的方法研究[J].国土资源遥感，2005，17(3):14-17.Mao K B，Shi J C，Li Z L，et al.The land surface temperature and emissivity retrieved from the AMSR passive microwave data[J].Remote Sensing for Land and Resources，2005，17(3):14-17.

[15]武胜利，杨 虎.AMSR-E亮温数据与MODIS陆表分类产品结合反演全球陆表温度[J].遥感技术与应用，2007，22(2):234-237.Wu S L，Yang H.Global land surface temperature retrieval with AMSR-E brightness temperature and MODIS land cover type products[J].Remote Sensing Technology and Application，2007，22(2):234-237.

[16]陈修治，陈水森，苏泳娴，等.利用AMSR-E遥感数据反演地表温度——以2008年广东省春季寒害为例[J].遥感信息，2011(5):38-46.Chen X Z，Chen S S，Su Y X，et al.Retrieving land surface temperature from AMSR-E remote sensing data:A case study over Guangdong during spring cold disaster in 2008[J].Remote Sensing Information，2011(5):38-46.

[17]Ulaby F T，Moore R K，Fung A K.Microwave remote sensing Ⅰ:Fundamentals and radiometry[R].Addison-Wesley Publishing Company，1981.

[18]Gao H，Wood E F，Jackson T J，et al.Using TRMM/TMI to retrieve surface soil moisture over the southern United States from 1998 to 2002[J].Journal of Hydrometeorology，2006，7(1):23-38.

[19]Gao H L，Fu R，Dickinson R E，et al.A practical method for retrieving land surface temperature from AMSR-E over the Amazon forest[J].IEEE Transactions on Geoscience and Remote Sensing，2008，46(1):193-199.

[20]Morland J C，Grimes D I F，Hewison，T J.Satellite observations of the microwave emissivity of a semi-arid land surface[J].Remote Sensing of Environment，2001，77(22):149-164.

[21]潘广东，王 超，张卫国，等.SSM/I微波辐射计数据中国陆地覆盖特征季节变化分析[J].遥感学报，2003，7(6):498-503.Pan G D，Wang C，Zhang W G，et al.Analysis of seasonal change of land cover characteristics with SSM/I data in China[J].Journal of Remote Sensing，2003，7(6):498-503.

[22]谷松岩，邱 红，张文建.先进微波探测器资料反演地表微波辐射率试验[J].电波科学学报，2004，19(4):452-457.Gu S Y，Qiu H，Zhang W J.Retrieval of land surface microwave emissivity by using satellite-borne AMSU data[J].Chinese Journal of Radio Science，2004，19(4):452-457.

[23]Weng F Z，Grody N C.Physical retrieval of land surface temperature using the special sensor microwave imager[J].Journal of Geophysical Research，1998，103(D8):8839-8848.

[24]You R，Yang H，Lu N M.Stability analysis of microwave emissivity in Simao Yunnan using SSM/I data[J].Journal of Remote Sensing，2009，13(5):887-893.

[25]Njoku E G.Surface temperature estimation over land using satellite microwave radiometry[C]//Choadhury B，Kerr Y，Njoku E G，et al.Passive microwave remote sensing of land-atmosphere interactions.Utrecht:The Netherlands’VSP，1995:509-530.

[26]Pulliainen J T，Grandell J，Hallikainen M T.Retrieval of surface temperature in boreal forest zone from SSM/I data[J].IEEE Transactions on Geoscience and Remote Sensing，1997，35(5):1188-1200.

[27]Xiang X W，Smith E A.Feasibility of simultaneous surface temperature-emissivity retrieval using SSM/I measurements from HAPEX-Sahel[J].Journal of Hydrology，1997(188/189):330-360.

[28]贾媛媛，李召良.被动微波遥感数据反演地表温度研究进展[J].地理科学进展，2006，25(3):420-425.Jia Y Y，Li Z L.Progress in land surface temperature retrieval from passive microwave remotely sensed data[J].Progress in Geography，2006，25(3):420-425.

[29]何文英，陈洪滨，宣越健，等.几种地表微波比辐射率变化特征的地面观测[J].地球物理学进展，2010，25(6):1983-1993.He W Y，Chen H B，Xuan Y J，et al.Field measurements of the surface microwave emissivity for different surface types[J].Progress in Geophysics，2010，25(6):1983-1993.

[30]Fily M，Royer A，Göita K，et al.A simple retrieval method for land surface temperature and fraction of water surface determination from satellite microwave brightness temperatures in sub-arctic areas[J].Remote Sensing of Environment，2003，85(3):328-338.

[31]毛克彪，王道龙，李滋睿，等.利用AMSR-E被动微波数据反演地表温度的神经网络算法[J].高技术通讯，2009，19(11):1195-1200.Mao K B，Wang D L，Li Z R，et al.A neural network method for retrieving land-surface temperature from AMSR-E data[J].Chinese High Technology Letters，2009，19(11):1195-1200.

[32]Zurk L M，Davis D，Njoku E G，et al.Inversion of parameters for semiarid regions by a neural network[C]//Proceedings of the International Geoscience and Remote Sensing Symposium(IGARSS)Houston:IGARSS，1992，2:1075-1077.

[33]陈修治，陈水森，李 丹，等.被动微波遥感反演地表温度研究进展[J].地球科学进展，2010，25(8):827-835.Chen X Z，Chen S S，Li D，et al.Progress in land surface temperature retrieval from passive microwave remote sensing data[J].Advances in Earth Science，2010，25(8):827-835.

[34]张文吉，张晓娟，李 芳.分层土壤后向散射及其在深层土壤湿度探测中的应用[J].电子与信息学报，2008，30(9):2107-2110.Zhang W J，Zhang X J，Li F.Backscattering from multilayer soil and its application to deep soil moisture estimation[J].Journal of Electronics and Information Technology，2008，30(9):2107-2110.

[35]吴 莹.微波地表发射率的卫星遥感反演和模式模拟研究[D].南京:南京信息工程大学，2012.Wu Y.Satellite remote sensing and modeling of microwave land surface emissivity[D].Nanjing:Nanjing University of Information Science and Technology，2012.