基于经验模态分解的MT数据脉冲类电磁噪声处理

王正海，耿 欣，姚卓森，胡光道，方 臣

1.中山大学地球科学系，广州 510275

2.中国科学院地质与地球物理研究所，北京 100029

3.中国地质大学资源学院，武汉 430074

0 引言

近年来，以天然电磁场为场源的大地电磁（MT）观测在深部矿产勘查和工程物探中应用广泛。但在应用中，由于噪声干扰，有用信息往往被噪声所掩盖，严重影响后续视电阻率和阻抗的计算及目标信息的提取[1-2]。如何利用采集得到的时间序列数据进行测区的噪声分析，从而进一步实现相应噪声的压制，是当前MT数据预处理的主要内容之一。脉冲类噪声是一种能引起电磁波的电脉冲，其强度很大，但持续时间较短，频带很宽，存在于MT信号低频段、中频段和高频段。脉冲干扰在频率域中没有任何明显特征，但是在时间域上，由于其能量很大，振幅是正常信号的几倍，非常容易识别[3-4]。因此，需要在时间域上寻找合适的方法进行脉冲类噪声抑制处理。

传统大地电磁法数据处理以常规傅里叶变换和功率谱分析为基础 ，通常假定信号为平稳或分段平稳，采用适当的分析方法，如傅里叶变换、小波变换等对 MT信号进行线性化处理[5-6]。近年来，很多学者已经证明大地电磁信号具有非平稳、非线性、非高斯的特征。上述基于线性平稳假设的处理方法不能很好地进行MT信号噪声处理。1998年，华裔科学家黄锷[7]提出了经验模态分解（EMD）算法，将信号分解成多个固有模态函数（IMF），且IMF是单分量函数；然后对每一个IMF进行Hibert变换，并定义瞬时频率，分析其时-频谱。EMD分解基于数据自身的特点，具有自适应的特征，而IMF又具有多尺度滤波的特点[7-8]。因此，EMD是处理非平稳、非线性信号的有效方法，被成功运用到流体力学、地震信号分析、基础结构监测等多个领域[9-10]。笔者主要讨论EMD在大地电磁测深系统信号分析和脉冲类噪声处理中的应用效果。

1 经验模态分解（EMD）

经验模态分解又叫Huang变换，为满足IMF为固有模态函数，它必须满足以下2个假设[9-10]：1）在整个数据序列中，极值点的数量与过零点的数量必须相等，或者最多相差不能多于一个。2）在任一时间点上，由局部最大值和局部最小值分别确定的2条包络线的平均值为0。

EMD分解通过三次样条方法多次迭代拟合实现：1）找出原始数据序列x（t）的局部最大值和局部最小值，采用三次样条方法拟合，得到信号的emax（t）和emin（t）。2）求每个时刻下emax（t）和emin（t）的平均值，即瞬时平均值m（t），代表着每一时刻信号的“瞬时平衡位置”：

3）用原始数据x（t）减去瞬时平均值 m（t），得到c1（t）：

式中，c1（t）被称为用原始数据的第一个本征模态函数分量（IMF）。然后，用原始数据减去c1（t）即可得到剩余数据r1（t）：

重复上述相同的迭代过程，通过EMD的一次次筛选，就可以获得信号的多个IMF分量和一个逼近分量rn（t），从而信号可表示为

经验模态分解其实是对非线性非平稳信号的一种平稳化处理，将信号中不同尺度的信息分解开来，使其产生的一系列不同尺度的信号均能满足后续Hilbert变换要求的窄带特性[11-12]。经验模态分解是完全可逆的，将分解所得的每一个序列信息逐一相加即可得到最初的原始信息。因此，经验模态分解可以在不同尺度下对数据进行处理后，再重新构建原数据，达到对原数据处理的目的。利用EMD变换进行信号处理时，针对不同目的，对每一阶IMF分量频谱进行相应处理，再分别利用式（4）进行信号重构，获得相应的信号处理效果。

2 脉冲干扰信号的EMD去噪

2.1 脉冲噪声分析

脉冲干扰多出现在电场中，电场中的脉冲干扰主要来源于测点附近介质层中的脉冲型游散电流，多为测点周围接地用电动力设备的开关或其负荷的突然改变造成的。电场和磁场中同时出现的脉冲干扰则多来自雷暴，或者是人类的电磁感应信号。

图1 EH-4实测数据中各频段的电磁脉冲干扰Fig.1 The electromagnetic pulse interference of the band of EH-4data

图1为西藏白容矿区利用美国EMI公司和Geo-metrics公司联合研制的EH-4大地电磁测深系统实测剖面28号测点的含脉冲干扰的MT信号，单纯的电脉冲较少出现，但是在几乎所有的测点内，都不同程度地出现了或多或少的电磁脉冲干扰。图1中低频段和高频段的电磁脉冲干扰在时间域中很明显地区分出来。由图1可知，该地区电磁脉冲能量极强，基本都达到了EH-4当前增益系数下的饱和测量值。在这种情况下，很多有用的信号都被强的电磁脉冲干扰所覆盖，不利于目标信息的提取及后续视电阻率和阻抗的计算。这类干扰若出现在电场中，将使阻抗的幅值严重向上偏移；而若出现在磁场中，则幅值向下偏移。

2.2 EMD去噪算法与步骤

EH-4大地电磁测深系统信号中脉冲干扰处理的关键是将脉冲噪声从MT信号中分离出来，进而对其进行相应处理，抑制脉冲干扰对MT信号的影响。

利用EMD变换进行脉冲干扰处理分三步进行：1）将受脉冲干扰影响的 MT信号x（t）经EMD分解后得到N个固有模态函数IMF；2）对每一阶的IMF选择一个合适的瞬时频率阀值，截断超出该阀值的部分，进行噪声处理；3）重建处理后的各IMF分量，得到去噪后信号。

利用EMD变换进行脉冲干扰处理的关键是如何确定消除脉冲干扰噪声的瞬时频率阀值。

对于第j阶固有模态函数，消除脉冲干扰噪声的瞬时频率阀值为

其中：N为IMF序列中所包含的数据数；k＝1或2，分别对应于数据的Gaussian分布和Rayleigh分布；是第j阶IMF的总体信号水平，定义为

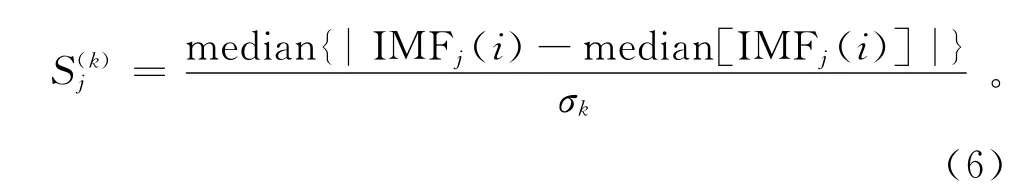
其中：IMFj（i）为第j阶IMF数据中第i个数据点的值，在整个时间域内取值；median[IMFj（i）]为第j 阶 IMF 的 中 位 差；median｛｜IMFj（i）-median[IMFj（i）]｜｝是第j 阶IMF 的绝对中位 差（MAD），也称为绝对中值偏差，相对于均方差来说，它对于脉冲干扰这种突起点，能够进行很好的抑制。σk是一个具有统计意义的固定常数：如果信号属于Gaussian分布，则σ＝0.6745；如果信号属于Rayleigh分布，σ＝0.4485。

式中：IMF′j（i）为阀值去噪后的IMFj（i）；w（i）为超出阀值部分的脉冲干扰进行加权处理的权函数。当第j阶IMF数据的绝对值超过阀值时，乘以权函数w（i），使得其值迅速减小；当数据的绝对值小于等于阀值时，保持不变。

Thomson函数具有严格的自适应性的稳健性，笔者选择Thomson函数作为权函数：

3 实例

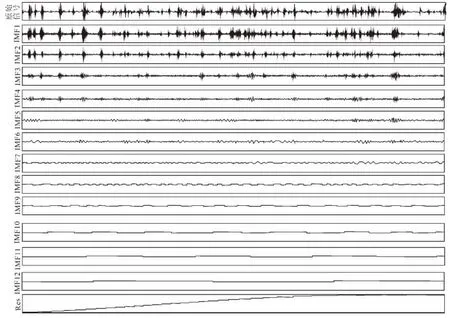
图2 28号测点中频段受脉冲干扰信号EMD分解各阶IMF图Fig.2 The intrinsic mode functions image of the medial signal interferenced by pulse at point 28

图3 受脉冲干扰信号EMD除噪处理前后效果对比图Fig.3 Comparison diagram of the interference signal processed by EMD transform

图4 EMD除噪处理前（a）后（b）所得视电阻率（ρa）对比图Fig.4 Comparison diagram of the resistivity before（a）and after（b）processing by EMD transform

将上述除噪方法应用于白容矿区EH-4实测剖面第28号测点中频段的Ex数据脉冲干扰处理，以验证该方法的有效性和合理性。将该数据进行EMD分解，共得到12阶IMF以及一阶Res（图2）。由于IMF1频率过高，表现为信号所包含的白噪声；Res为低频趋势项。采用式（5）分别计算各阶IMF序列的阀值，并用此阀值对各阶数据值进行修正，对超出的脉冲部分采用式（7）进行加权处理，最后得到消噪后的信号（图3）。可以看出，原始数据在时间域明显受到了脉冲干扰（图3a）；经过消噪处理后的时间序列，很显然对脉冲干扰的抑制和消除效果显著（图3b）；图3c是将消噪处理后的数据选择一个合适的比例尺来表现，这样可以将被脉冲干扰压制的信号细节信息展示出来。经过仔细对比，可以发现，这种除噪方法不仅消除了脉冲干扰的影响，而且保留甚至更细致地刻画出信号的局部信息。

将经过EMD除噪后的信号重新输入EH-4数据处理系统，经过计算所得的视电阻率曲线与未处理数据形成了鲜明的对比（图4）。未处理的信号由于脉冲干扰的影响，在相位和视电阻率上经常出现较大间断和数值的突然增加；而经过除噪后，整个信号显得更加连续和可靠，有效地提高了数据的可信度和质量水平。

4 结论

1）EMD变换可以分解出多阶IMF序列，属于一种从高频到低频的层层筛分过程，可以将信号分为若干个不同的具有各自物理意义的序列，是一种多尺度、多分辨分析的滤波过程。

2）利用EMD变换进行大地电磁测深（MT）信号脉冲类干扰去除的关键是如何选择一个合适的瞬时频率阀值，对MT信号经EMD分解后得到N个固有模态函数IMF进行噪声筛选，然后进行EMD重构。笔者提出的利用绝对中位差结合Thomson权函数对各阶IMF进行噪声筛选是可行、有效的。

3）实测数据处理表明，利用EMD变换进行大地电磁测深（MT）信号脉冲类干扰处理，改正前后信号的相关性高，能量损失小，能有效消除MT信号中脉冲类干扰。

（References）：

[1]化希瑞，曹哲明，刘铁，等.高频大地电磁系统数据处理方法研究[J].工程地球物理学报，2009，6（增刊）：25-32.Hua Xirui，Cao Zheming，Liu Tie，et al.The Research on High-Frequency Magnetotelluric System’s Data Processing Technique[J].Chinese Journal of Engineering Geophysics，2009，6（Sup.）：25-32.

[2]孙洁，晋文光，白登海，等.大地电磁测深资料的噪声干扰[J].物探与化探，2000，22（2）：120-127.Sun Jie，Jin Wenguang，Bai Denghai，et al.The Noise Interference of Magnetotelluric Sounding Data[J].Geophysical and Geochemical Exploration，2000，22（2）：120-127.

[3]席振铢，龙霞，董晨，等.EH-4系统中工频干扰的处理与改进[J].地球物理学进展，2010，25（3）：1105-1109.Xi Zhenzhu，Long Xia，Dong Chen，et al.An Improved Method to Eliminate the Power-Line Interference in the EH-4System[J].Progress in Geophysics，2010，25（3）：1105-1109.

[4]蔡剑华，汤井田，王先春.基于经验模态分解的大地电磁资料人文噪声处理[J].中南大学学报：自然科学版，2011，42（6）：1786-1790.Cai Jianhua，Tang Jingtian，Wang Xianchun.Human Noise Elimination for Magnetotelluric Data Based on Empirical Mode Decomposition[J].Journal of Central South University：Science and Technology，2011，42（6）：1786-1790.

[5]严家斌，刘贵忠.基于小波变换的脉冲类电磁噪声处理[J].煤田地质与勘探，2007，35（5）：61-65.Yan Jiabin，Liu Guizhong.Like-Impulse Electromagnetic Noise Processing Based Wavelet Transform[J].Coal Geology ＆ Exploration，2007，35（5）：61-65.

[6]Trad O D，Travassos M J.Wavelet Filtering of Magnetotelluric Data[J].Geophysics，2000，65（2）：482-491.

[7]Huang E N.The Empirical Mode Decomposition and Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[M].London：Proc R Soc，1998.

[8]Huang E N，Wu Zhaohua.A Review on Hilbert-Huang Transform：The Method and Its Applications on Geophysical Studies[J].Rev Geophys，2008，46：1-23.

[9]Huang E N，Shen S S P.The Hilbert-Huang Transform and Its Applications[M].[S.l.]：World Scientific Publishing Co Pte Ltd，2005.

[10]汤井田，化希瑞，曹哲民，等.Hilbert-Huang变换与大地电磁噪声压制[J].地球物理学报，2008，51（2）：603-610.Tang Jingtian，Hua Xirui，Cao Zhemin，et al.Hilbert-Huang Transformation and Noise Suppression of Magnetotelluric Sounding Data[J].Chinese Journal of Geophysics，2008，51（2）：603-610.

[11]董烈乾，李振春，刘磊，等.基于经验模态分解的曲波阈值去噪方法[J].吉林大学学报：地球科学版，2012，42（3）：838-844.Dong Lieqian，Li Zhenchun，Liu Lei，et al.A Method of Curvelet Threshold Denoiosing Based on Empirical Mode Decomposition[J].Journal of Jilin University：Earth Science Edition，2012，42（3）：838-844.

[12]陈凯.基于经验模式分解的去噪方法[J].石油地球物理勘探，2009，44（5）：603-608.Chen Kai.A New Denoising Method Based on Empirical Mode Decomposition（EMD）[J].Oil Geophysical Prospecting，2009，44（5）：603-608.