一种悬浮石墨烯压力传感器的制造与建模*

蒋圣伟， 师 帅， 袁娇娇， 方 靖， 徐春林， 汪学方

(华中科技大学 机械科学与工程学院微系统中心，湖北 武汉 430074)

0 引 言

石墨烯是一种新兴半导体材料，其发现者荣获2010年诺贝尔物理学奖。单层石墨烯的厚度仅为一个原子厚度[1](约为0.335 nm)，具有独特优异的机械与电学性质，石墨烯目前是世上最薄却也是最坚硬的纳米材料，杨氏模量为1 TPa[2]，电子迁移率高达200 000 cm2/Vs[3]，石墨烯薄膜与SiO2基底之间的粘附性很强[4]，且对于气体具有不可穿透性[5]。基于石墨烯这些优异性质，科学家提出并研究了多种石墨烯压力传感器。Ma J等人[6]提出一种光纤石墨烯压力传感器，具有结构紧凑与低温度灵敏度高等优点，可应用于井下、深海等恶劣环境。浙江大学的Xu Y等人[7]提出了面内或隧穿石墨烯压力传感器，量程大，最大检测压力可达5 GPa。Kwon O K等人[8]提出了一种极高灵敏度石墨烯压力传感器，适用于低压检测环境。

本文提出了一种悬浮石墨烯压力传感器的制造工艺与建模。用高定向热解石墨(HOPG)机械剥离出石墨烯，并研究了不同厚度石墨烯的拉曼光谱。基于薄膜膨胀试验，对薄膜力学性质与灵敏度进行了理论建模。

1 压力传感器结构与制造

如图1所示，悬浮石墨烯压力传感器与传统MEMS压力传感器的主要区别在于感知压力的薄膜不同。石墨烯薄膜悬浮在矩形空腔上方并吸附在SiO2表面，当石墨烯薄膜内外存在压差时，由于压阻效应其电阻将改变，通过外部电路可以检测电阻变化。

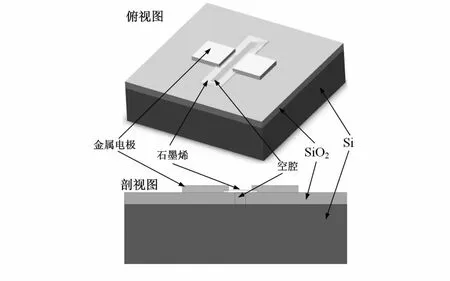
图1 悬浮石墨烯压力传感器结构示意图

如图2所示，悬浮石墨烯压力传感器的制造过程分为5步：

1)取一Si片(400 μm厚)，表面附有一层300 nm厚的SiO2，将Si片切成12 mm×12 mm小块；

2)对硅片进行光刻，采用ICP刻蚀得到空腔，空腔刻蚀厚度为10 μm，空腔可为矩形、圆形或者方形；

3)将化学气相沉积法(CVD)得到的石墨烯薄膜转移到SiO2/Si基底上；

4)对石墨烯薄膜进行光刻，使用氧等离子体刻蚀将薄膜分割成矩形小块，每个小块分别覆盖一个空腔；

5)通过光刻得到金属电极图案，利用电子束蒸发在图案处先后沉积20 nm的Ti和200 nm的Au。

图2 悬浮石墨烯压力传感器的制造过程

第3步石墨烯薄膜的转移是关键，转移前需要保证基底表面清洁平整，转移后进行干燥以除去残留在空腔中的去离子水。图3详细描述了转移过程。

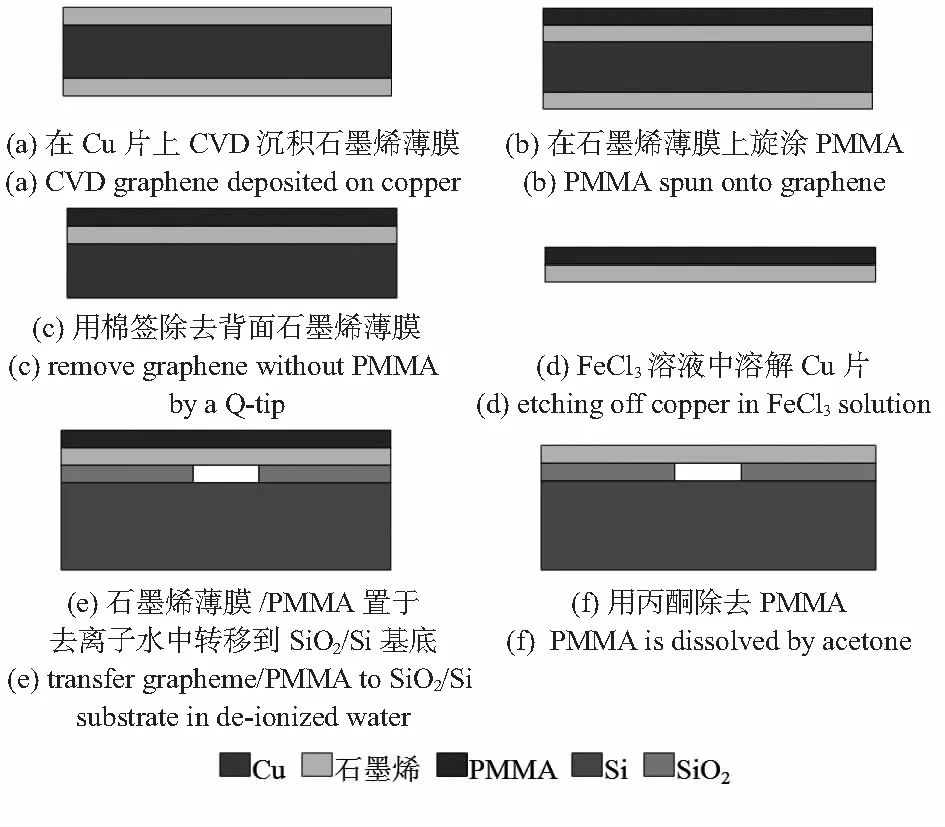
图3 石墨烯薄膜的转移过程

2 机械剥离石墨烯与拉曼表征

采用Scotch透明胶带对高定向热解石墨(HOPG)进行反复剥离，剥离10次后石墨片越来越薄，越来越分散，将附着石墨薄片的胶带粘附在硅片(抛光一面)上并轻轻压实，使胶带与硅片完全粘附，保持15 min后缓慢撕掉胶带，这时，硅片表面会留下大量石墨薄片。图4为所选的一个剥离样品，石墨烯厚度不同，其颜色深浅不同。

图4 机械剥离法得到的石墨烯样品的光学显微镜图像

图5所示为4种颜色深浅不同区域的石墨烯的拉曼光谱，Δσ为拉曼位移，从中可以看出：“G”峰与“2D”峰分别位于1 580 cm-1与2 680 cm-1附近，二者的强度与形状均不同，这与文献[9]相符，石墨烯区域颜色由浅向深变化(层数增加)时，“G”峰强度与“2D”峰强度均增大，且“2D”峰逐渐向高波数方向移动。石墨烯层数高于双层时，“G”峰强度高于“2D”峰[9]，因此，图4得到的都是多层石墨烯。机械剥离法难以得到大面积单层石墨烯，在制造悬浮石墨烯压力传感器时应采用CVD法[10]，可得到均匀性一致的单层或多层石墨烯。

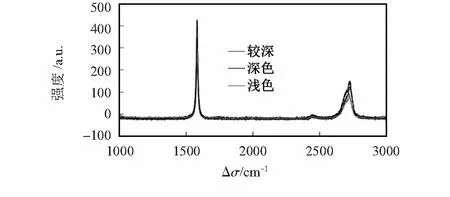
图5 不同厚度石墨烯的拉曼光谱

3 膨胀试验法建模

膨胀试验(bulge test)是一种普遍使用的方法，用来测量薄膜的平面机械性质，包括：杨氏模量、泊松比、残余应力。这里已知石墨烯薄膜的杨氏模量、泊松比和残余应力，来分析不同空腔形状时受力薄膜的变形、应变及压力灵敏度。

以矩形空腔为例[11]，如图6所示，在沿长度方向夹紧的矩形薄膜上施加一个压差p，矩形空腔长为L，宽为w，薄膜顶端的曲率半径为R，薄膜厚度为t，最大变形为z，压差p与薄膜内诱导的双轴应力σ保持平衡

2R·L·p=2t·L·σ,

(1)

(2)

图6 薄膜膨胀试验示意图

小变形时,z≪w/2，利用勾股定理可得到曲率半径R与矩形空腔宽度w的关系

(3)

将式(3)代入式(2)中可得

(4)

薄膜表面张力为

(5)

薄膜应变为

(6)

对于矩形空腔，薄膜应变与应力满足

(7)

式中E和ν分别为薄膜的杨氏模量和泊松比。对于石墨烯薄膜，E=1 TPa，ν=0.16。

薄膜表面张力由2种表面张力叠加而成，一种是由于应变诱导的表面张力SP，一种是残余应力σ0产生的表面张力S0,其中

(8)

S0=σ0t.

(9)

因此,可得到关系式

(10)

压差大小为

(11)

同理,可推导出方形空腔与圆形空腔对应的压差大小为

(12)

式中c1=3.393，c2=(0.8+0.062ν)-3为2个常数，w为方形边长

(13)

式中w为圆形直径。

由文献[5]可知，石墨烯的表面张力S0为0.1 N/m，为方便与文献[12]的有限元计算结果进行对比，取w=6 μm，计算了矩形、方形与圆形空腔时单层石墨烯薄膜的最大变形与压差的关系，如图7所示。可以看出:3种情形下关系曲线变化相似，矩形时曲线更为陡峭；压差相同时，矩形空腔的表面最大变形最大，圆形最小；在压力较小的范围内，石墨烯薄膜的变形极为灵敏；矩形情况下压差为47.7 kPa时的最大变形为197 nm，这与文献[12]的202 nm相符合。目前在已有文献中有实验[4,5]与有限元模拟[12]2种方法计算石墨烯薄膜的最大变形，在同等条件下，本文运用膨胀试验的计算值与上述2种方法进行了对比，如表1，可知三者结果相近，验证了本文方法的可行性。如图8所示，薄膜应变的膨胀试验与COMSOL计算结果基本一致，而实验测量石墨烯压阻系数时无法直接测量石墨烯应变，此方法是一种很好的选择。

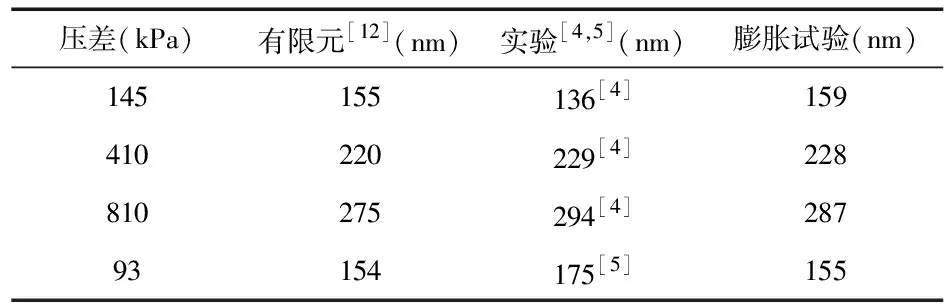
表1 有限元、实验与膨胀试验三者方法得到的石墨烯薄膜最大变形的比较

图7 单层石墨烯薄膜最大变形与压差的关系

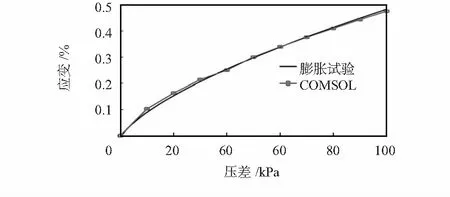
图8 单层石墨烯薄膜应变与压差的关系

定义最大变形的变化率的大小Δz/Δp为压力传感器的压力灵敏度，则石墨烯薄膜的压力灵敏度与空腔尺寸、石墨烯厚度有关。如图9所示，在压差为5 kPa处，矩形宽度、方形边长或者圆形直径越大时，压力灵敏度越大，圆形直径为25 μm时，压力灵敏度为97.2 nm/kPa，大于文献[6]中相同直径时光纤石墨烯压力传感器的39.4 nm/kPa。如图10所示，石墨烯薄膜层数增大时，压力灵敏度减小，且当层数高于7层时，压力灵敏度变化缓慢，因此,在制造高灵敏度悬浮石墨烯压力传感器时应选用单层或双层石墨烯薄膜。

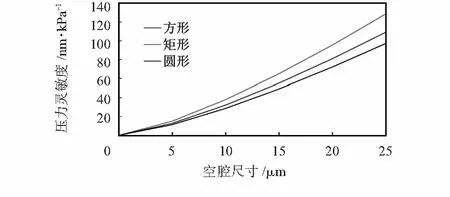
图9 单层石墨烯薄膜压力灵敏度与空腔尺寸的关系

图10 石墨烯薄膜压力灵敏度与石墨烯层数的关系

4 结 论

本文提出了一种悬浮石墨烯压力传感器，制造工艺简单，结构紧凑，灵敏度高。通过机械剥离法实验制备了石墨烯，并用拉曼光谱对石墨烯进行了表征，石墨烯厚度增大时，“G”峰强度与“2D”峰强度均增大，且“2D”峰逐渐向高波数方向移动，但石墨烯厚度与尺寸分布不均匀，不利于应用在石墨烯压力传感器的制造。薄膜膨胀试验方法验证了这种压力传感器的高灵敏度，且进一步得出矩形空腔时的压力灵敏度大于方形与圆形空腔，当矩形宽度、方形边长或圆形直径越大，薄膜厚度越小时，压力灵敏度越高。这种压力传感器可用于纳机电系统(NEMS)，在医学、生物等纳米领域具有巨大的应用潜力。

参考文献:

[1] Novoselov K S,Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films [J].Science,2004,306(5696):666-669.

[2] Lee C,Wei X,Kysar J W,et al.Measurement of the elastic pro-perties and intrinsic strength of monolayer graphene [J].Science，2008,321(5887):385-388.

[3] Bolotin K I,Sikes K J,Jiang Z,et al.Ultrahigh electron mobility in suspended graphene [J].Solid State Communications,2008,146(9-10):351-355.

[4] Koenig S P,Boddeti N G,Dunn M L,et al.Ultrastrong adhesion of graphene membranes [J].Nature Nanotechnology,2011,6(9):543-546.

[5] Bunch J S,Verbridge S S,Alden J S,et al.Impermeable atomic membranes from graphene sheets[J].Nano Letters,2008,8(8):2458-2462.

[6] Ma J,Jin W,Ho H L,et al.High-sensitivity fiber-tip pressure sensor with graphene diaphragm[J].Optics Letters,2012,37(13):2493-2495.

[7] Xu Y,Guo Z D,Chen H B,et al.In-plane and tunneling pressure sensors based on graphene/ hexagonal boron nitride heterostructures [J].Applied Physics Letters,2011,99(13):133109—1-133109—3.

[8] Kwon O K,Lee J H,Kim K S,et al.Developing ultrasensitive pressure sensor based on graphene nanoribbon:Molecular dyna-mics simulation [J].Physica E,2013,47:6-11.

[9] Ferrarl A C,Meyer J C,Scardaci V,et al.Raman spectrum of graphene and graphene layers [J].Physical Review Letters,2006,97(18):187401—1-187401—4.

[10] Li X S,Cai W W,An J H,et al.Large-area synthesis of high-quality and uniform graphene films on copper foils [J].Science,2009,324(5932):1312-1314.

[11] Bunch J S.Mechanical and electrical properties of graphene sheets[D].New York:Cornell University of NewYork,2008.

[12] Smith A D,Niklaus F,Paussa A,et al.Electromechanical piezoresistive sensing in suspended graphene membranes[J].Nano Letters,2013,13(7):3237-3242.