基于分布式压缩感知的能量收集WSNs*

汪鲁才, 赵延昇, 林海军, 刘国锋

(湖南师范大学 工程与设计学院 电子系，湖南 长沙 410012)

0 引 言

无线传感器网络(WSNs)[1]在环境监测、结构健康监测、植入式医疗监测、汽车胎压监测等方面有广阔的应用前景，但是这些应用的主要瓶颈是自给能源。如果每个节点都需要自己的外部电源，那么WSNs就失去了优势。而能源收集[2]能将局部环境能量转换成可用的电能，成为了一种给WSNs供电的方法。能源收集是指传感器节点应该采用尽可能多的方法从环境中吸取能量,以确保传感器节点能够长期、稳定、可靠地工作。目前，WSNs应用能源收集装置是一种流行的趋势。通过能源收集，WSNs所需能源能够自足，网络的应用寿命更长。

目前，针对能源收集的WSNs出现了很多新型的数据获取和传输机制的设计。例如：文献[3]通过描述能量来源的复杂时提出变性解析易处理模型；文献[4]提出了吞吐量优化和平均延迟优化的能源管理策略；文献[5]提出通过注水法则算法来最大化能源生产，同时最小化网络通信的传输时间。目前出现的诸多能源管理方法并没有把能量收集的过程和WSNs中能量多样性和传输多样性有机的融合起来。

本文应用分布式压缩感知(distributed compressed sen-sing,DCS)[6,7]来延长WSNs寿命和提高数据采集率，理论分析了应用DCS使得特定条件下WSNs中信号的收集、传输和高效的能源管理结合起来。实验证明在同样恢复出所需信号的情况下，每个传感器节点传送的测量数据的维数将比原始数据维数低很多。在能源收集和能源消耗之间达到尽可能的平衡，为实现节能环保的WSNs提供一个新的方向。

1 系统设计与DCS

1.1 系统模型

考虑一个典型的基于聚类的WSNs结构，结构图见图1。一系列的节点定期地向一个或多个簇头传输数据。

图1 典型的基于聚类的WSNs结构图

定义一个周期T，假设节点在周期T内有T0秒活动时间是采集数据并向簇头传输，而在(T-T0)秒是空闲的，来从周围环境中进行能源收集，见图2。

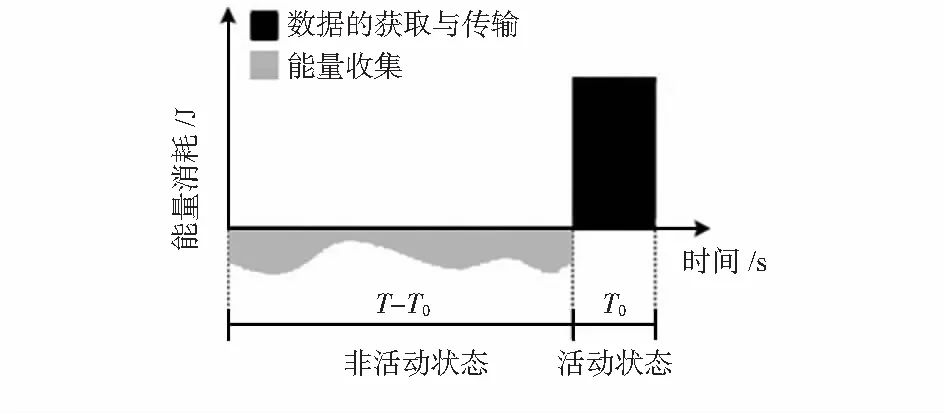
图2 节点能量收集消耗描述图

本文WSNs模型假设共有K个节点，同时保证WSNs满足JSM—1模型[8]。在这个模型中，原始信号fk(i)∈Rn(i)在稀疏基ψ(i)∈Rn(i)×n(i)下是稀疏的,即每个节点在第i次需要采集的原始信号fk(i)为

fk(i)=ψ(i)xk(i).

(1)

其中,xk(i)∈Rn(i)为稀疏信号，稀疏度为‖xk(i)‖0=sk(i)。JSM—1模型中，信号群中所有的信号拥有共同的稀疏成分，但是,每个独立信号又包含一个稀疏独立成分[9]。所以,xk(i)可以表示为

xk(i)=zc(i)+zk(i).

(2)

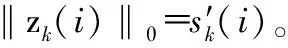
WSNs数据的采集受到能源收集的约束,尤其是，假定传感节点在每个活动期间必须遵守一定的能量预算方案,即

(3)

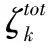
ζk(i)≥τmk(i).

(4)

为了便于分析，认为ζk(i)在区间[(1-α)μ，(1+α)μ]满足均匀分布。μ为收集能量的平均值，α为系数满足0<α≤1。

针对上述模型，为了建立更好的节能环保的WSNs，引入一种新的数据融合理论—DCS理论。

1.2 DCS理论

DCS 理论是在信号群的联合稀疏的概念上建立起来的。如果多个信号均在某个基下稀疏，且这些信号彼此之间具有相关性，那么每个信号都能通过利用另一个不相关的基矩阵来进行观测和编码，然后得到远小于原信号长度的编码。将每个信号编码后的少量数据分别传输到解码端，那么，在适当的条件下，解码端再利用这些数据就能精确重建这个信号群中的每一个信号。关键技术在于：1)基于DCS数据采集；2)数据传输；3)基于DCS的数据重建。

1.2.1 数据采集

传感器节点利用DCS对原始的高维数据采样，得到低维的采样值。每个节点在第i次活动期间t(iT-T0≤t≤iT)内的采样值为

yk(i)=Φk(i)fk(i)=Φk(i)ψk(i)xk(i).

(5)

yk(i)∈Rm(i)为传感器节点采集的数据，Φk(i)∈Rm(i)×n(i)为测量矩阵。值得注意的是:每次在采集数据的维数在每个节点和每个时间段都可以是不同的。

1.2.2 数据传输

WSNs中的节点将采集到的低维测量值传送到簇头。为了防止传送数据不出现冲突碰撞，认为每个与同一簇头通过特定信道相连的节点是一种时频稳态模式。为了便于分析，同时假设外部的干扰和噪声在数据包的传送过程中通过传感网络物理层调制处理干净。这样，采样值的传送过程中不会出现冲突，信号的传输损耗基本可以忽略。

1.2.3 数据恢复

众所周知，传统的CS[10]单独的恢复不同节点的每一个信号。数学式如下

Ak(i)xk(i)=yk(i).

(6)

文献[11]指出，当空间采样有规律时，利用CS采样机制来恢复信号比较简单明了，但一旦空间采样不规则，表示信号的稀疏就非常困难。此外，由于CS重构都是针对单一时间段分别重构，它仅仅利用了信号内部的相关性，而没有利用信号间的相互关联。

而DCS则是一次性的重构出多个信号,数学式如下

(7)

其中

(8)

对比DCS和CS信号重构可以发现，基于能源管理的DCS重构充分利用了传感器节点间和节点内的相关性，提高了传感网络的效率。

2 基于能源收集采样机制比较

为了阐述能源收集的WSNs各个采样机制下的特点，考虑最简单的情况，由2个节点组成的WSNs，对比3种不同的方法所具有的特性。

2.1 传统采样机制

传统采样机制中采样的数据维数为n维。要满足式(4)，即ζ1≥τn，ζ2≥τn。当能源的收集小于能源的消耗时，信号不能正确重构。因此,在传统采样机制下，信号错误重构的概率为

P0≥1-P(ζ1≥τn,ζ2≥τn).

(9)

由于P(ζ1≥τn,ζ2≥τn)满足均匀分布，所以

P0≥1-P(ζ1≥τn,ζ2≥τn)

(10)

2.2 CS 采样机制

假定2个传感器节点采样的信号满足同样的稀疏度s=s1=s2。从文献[12]可知当测量数据维数mk≥sklog(n/sk)，压缩感知能实现对信号的近乎完全重构，所以，m1=m2=slog(n/s)。为了满足式(4)，可以得出在CS采样机制下，信号错误重构的概率为

Pcs≥1-P(ζ1≥τm1,ζ2≥τm2)

(11)

2.3 DCS采样机制

因此,在DCS采样机制下，信号错误重构的概率为

(12)

以上分析可知，在满足能源收集的WSNs中，DCS的重构错误概率最低。为了直观的展示这一特征，令α=0.5，n=104，s=103，s′=200，sc=800，u/τ定义为能源利用率。Matlab仿真得出3种机制错误重构概率图,见图3。

图3 WSNs信号错误重构概率

3 实验仿真

实验中，产生一个稀疏信号Xk(k=1,2,3,…,K)，维数n=50。其中非零原子满足独立同分布的标准正态分布。测量矩阵Ak(k=1,2,3,…,K)采样随机高斯矩阵。

图4说明了信号错误重构的概率和能源利用率之间的关系，其中,K=2，sc=5，s′=1。对比可知，DCS要求WSNs能源收集的能力比其他2种机制都要低。错误重构的概率达到0.01时，DCS要求的能源利用率只需要达到26，而CS要求34，传统的采集机制要求更是远远高于这2种机制。

图4 错误重构概率与能源利用率关系图

图5说明了信号错误重构的概率与WSNs中节点数目的关系，其中sc=5，s′=1。由图可知，在CS机制下随着传感节点的增加，信号错误重构的概率变大。因为节点的增加，其中某些节点因为能源收集的不够而导致WSNs无法正确的完成信号的测量和传输的概率变大，导致信号错误重构的概率也变大。而DCS机制下，错误重构的概率随着节点数的增加先是降低的然后再升高。这正体现了DCS利用了节点信号间的相关性。

图5 错误重构概率与节点数关系图

图6说明了信号正确重构的概率与测量数目的关系，其中sc=5，s′=1。由图可知，相同测量值情况下，基于DCS机制的WSNs正确重构概率明显高于CS机制的WSNs。这样显著降低传输的测量速率，从而节省了传感器节点的能量消耗。

图6 正确重构概率与测量值的关系

4 结 论

本文从能源收集的角度来阐述应用DCS在WSNs上的优越性。能源的多样性和传感信号的多元化为基于DCS数据采集模式的WSNs的能量需求和能量供应提供了基础和保障。通过理论分析和实验仿真，基于DCS的数据采集模式与其他采集模式(如CS)相比，达到相同的重建质量，DCS采集模式需要更少的测量值，重建的错误概率更低，大大降低了WSNs的能耗，提高了能源的利用效率。

参考文献:

[1] Pottie G,Kaiser W.Wireless sensor networks[J].Communications of the ACM,2000,43(5):51-58.

[2] Priya S,Inman D J.Energy harvesting technologies[M].Chicago:Springer,2008.

[3] Kansal A,Hsu J,Zahedi S,et al.Power management in energy harvesting sensor networks[J].ACM Transactions on Embedded

Computing Systems,2007,5(2):12-32.

[4] Sharma V,Mukherji U,Joseph V,et al.Optimal energy management policies for energy harvesting sensor nodes[J].IEEE Transactions on Wireless Communications,2010,9(4) :1326-1336.

[5] Ozel O,Tutuncuoglu K,Yang J,et al.Transmission with energy harvesting nodes in fading wireless channels:Optimal policies selected areas in communications[J].IEEE Journal on Selected Areas in Communications,2011,29(8):1732-1743 .

[6] Baron D,Duarte M F,Sarvotham S,et al.An information-theoretic approach to distributed compressed sensing[C]∥Proc of 43rd Allerton Conf on Communication,Control and Computing,Monticello,IL,2005:1295-1306.

[7] Chou J,Petrovic D,Ramchandran K.A distributed and adaptive signal processing approach to reducing energy consumption in sensor networks[C]∥Proc of IEEE Infocom,2003:1054-1062.

[8] Baron D,Duarte M F,Sarvotham S,et al..Distributed compressed sensing of jointly sparse signals[J].IEEE Digital Object Identifier,2005,10( 7) :1537-1541.

[9] Wakin M B,Sarvotham S,Duarte M F.Recovery of jointly sparse signals from few random projections[J].Computer Simulation,2008,25(3):214-217.

[10] Donoho D L.Compressed sensing[J].IEEE Transformation on Information Theory,2006,52(4):1289-1306.

[11] Wagner R,Delouille V,Choi H,et al.Distributed wavelet transform for irregular sensor network grids[C]∥Proc of IEEE Statistical Signal Processing Workshop,Bordeaux,France,2005:1196-1201.

[12] Candès E J,Wakin M B.An introduction to compressive samp-ling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.

[13] Baron D,Wakin M B,Duarte M F.Distributed compressed sen-sing.[EB/OL].[2005—11—27].http:∥www.dsp.rice.edu/～drorb/pdf/DCS112005.Pdf.