视觉引导的旋转对称激光三角传感器快速测量方法*

高亚捷， 高 隽， 张旭东， 高欣健， 胡良梅

(合肥工业大学 计算机与信息学院,安徽 合肥 230009)

0 引 言

随着科学技术快速发展，人们对精密测量的要求也越来越高，并不断向智能化、集成化、高效率的方向发展。基于激光三角法的精密测量是一种比较常用的测量技术，激光三角法是一种经典的光电检测方法，这种测量技术具有结构简单、抗干扰能力强、使用灵活方便等优点。传统的激光三角技术已趋于成熟，基于此原理的激光三角传感器产品也较多。目前,国内外关于激光三角传感器的研究虽然较多，但主要集中于与CCD的集成、系统平台的搭建和测量精度控制等方面[1,2]，而在如何优化测量过程，提高测量效率方面，研究相对较少。张洪等人[3]研究了一种视觉引导下的曲面三坐标测量机(CMM)测量,国外有Seokba Son等人[4]设计了一种自由曲面的自动扫描系统。但张洪和Seokba Son的方法需要了解被扫描物体的表面方程等信息，当缺失相关信息时，方法也会失效。

从国内外研究现状可知，当对物体自身信息了解较少时，没有一种通用的测点生成算法，可以在保证测量精度的同时，减少扫描点数，提高效率。

本文在合肥工业大学图像信息处理实验室和德国海尔布隆大学光学实验室合作研制的旋转对称激光三角传感器[5](rotational symmetric laser triangulation sensor,RSTS)基础上，提出了一种视觉引导的测量方法,快速精确获取目标深度数据并进行三维重建。

1 视觉引导的测量方法

1.1 旋转对称激光三角传感器

传统激光三角传感器中，当激光投射至阶跃表面，或在返回过程中碰到遮挡，均会导致无法获取有效距离信息。旋转对称激光三角传感器克服了该结构缺点，使用一种全对称方式，在对物体表面测量时，CCD上会形成一个圆环，圆环半径代表了深度信息[6]。

根据旋转对称激光三角传感器的结构特点，如图1所示，可知在对阶跃表面进行测量，或光线返回过程中受到遮挡，会导致无法获取完整的圆环，出现圆环缺失或仅有半圆的情况。但只要有圆上3个点的信息，即可计算出圆环半径，而已知圆环半径和深度信息呈线性关系[7]。

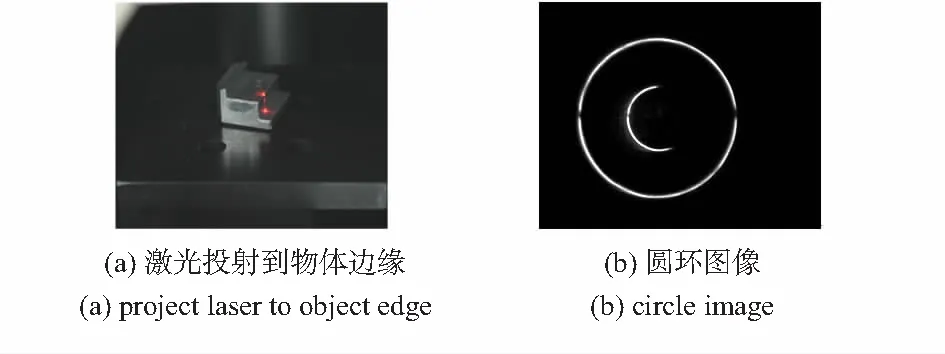
图1 测量阶跃边缘的情况

1.2 集成视觉的旋转对称激光三角传感器

旋转对称激光三角传感器虽可以获取精确的深度信息，但关于物体的表面形状和结构信息较少。为达到视觉引导测量的目的，本文在激光测量系统基础上，又集成了视觉系统。如图2所示，在传感器底部，添加一个环状LED光源，通过LED光源可以直接获取目标物体的图像。

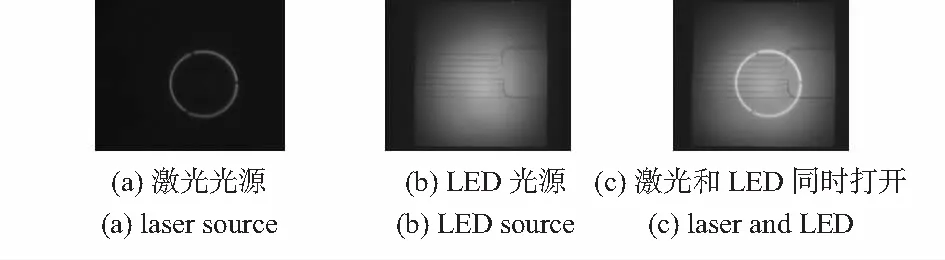
图2 不同光源下CCD获取的图像

1.3 视觉引导的激光三角测量方法

集成视觉的旋转对称激光三角传感器克服了传统激光三角传感器的一些缺陷，但仍需对物体逐点测量，速度慢，效率低。本文旨在对物体信息完全未知的情况下，给出一种高效率、精确的视觉引导测量方法。本文的处理对象是一些工业上常用的工件。对于普通工件，利用旋转对称激光三角传感器所集成的视觉系统获取工件图像，通过边缘提取技术对物体进行分块，而这些边缘特征代表了一些跳跃的深度信息，需要密集采样测量。在这些边界内部，通常为光滑曲面或平面，结构相对简单，因此，进行相对稀疏的采样测量。

前沿推进技术(AFT)方法[8]是一种平面非结构化网格生成方法，该方法在获取物体边界后，将其离散化作为前沿点序列，并以此为基础向物体内部推进生成新点。该方法中边界点的采样和内部节点的疏密均可以通过参数控制，且内部生成的新节点分布合理，契合了本文对激光测量点的要求。因此，本文采用了基于AFT方法的网格生成方法，作为视觉引导的测量点，引导旋转对称激光三角传感器对这些指定点进行测量。该方法流程如图3所示。

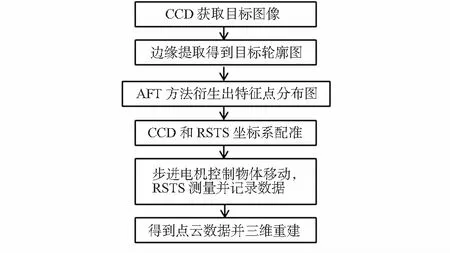
图3 视觉引导的测量方法流程图

2 AFT的视觉引导方法

AFT方法是目前较为流行和应用广泛的全自动非结构化网格生成算法之一，它适用于网格生成的诸多领域。本文在初始的AFT方法基础上，结合目标的几何特征，设计一种适应目标几何特征的AFT方法，通过增加距离系数，控制内部节点的稀疏，达到测量要求。

2.1 离散边界曲线

采用常用的Canny算子，首先对CCD获取的灰度图像进行边缘提取，提取出的边缘，通常会分为单连通区域和复连通区域。AFT方法以点为基础，向内部生成新点，因此，首先需要将边缘曲线离散化为点序列。

2.1.1 采样边界曲线

设某边界上有n个采样点，si和si+1为2个相邻的采样点，p为位于si和si+1之间的一个曲线点，3个点到曲线起始点的弧长分别为li,li+1和lp，另记hi,hi+1为si和si+1处的尺寸值，则si和si+1之间的网格尺寸分布为

(1)

2.1.2 计算边界曲线上最终的离散边数目

由上面公式可知，si,si+1之间的离散边数目为

(2)

这条边上总的离散边数目为

(3)

2.1.3 计算最终离散点坐标

为了计算第i个离散点gi，找到这样一个k，使得ni第一次满足nk≤ni≤nk+1，另记lg,lk,lk+1分别为gi,sk,sk+1到曲线起始点的弧长，hg,hk,hk+1为三点处的尺寸值，联立方程组为

(4)

可解得lg,然后利用数值迭代方法，根据弧长lg计算最终离散点的物理坐标。对于复连通区域，可以得到内外2个边缘点集。

2.2 计算图像节点的距离系数

AFT方法在向内部生成节点时没有固定的计算公式，本文为了使靠近边缘处点更稠密，远离边缘处点更稀疏，引入了距离系数dp。对于内部节点p通过该系数控制新点到三角形底边的距离长短。dp=min(dpW,dpW1),其中,dpW,dpW1为生成点p到内外边缘点集的最近距离

(5)

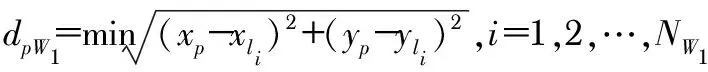
(6)

2.3 基于距离系数的内部节点更新

2.3.1 生成候选节点

分别计算A,B两点处的距离系数，过AB中点O作中垂线，长度l计算公式为l=c×edp，由此生成新节点P1，c为控制系数，一般取固定值。

2.3.2 确定前沿点

如图4所示，生成新的前沿点P1后，以R=0.5×AB为半径搜索附近是否有其它前沿点。如在P4点处，搜索到点B1，则以B1取代P4作为前沿点。如果在搜索过程中发现有多个候选点，则比较三角形的质量，以形状最接近正三角形的点作为前沿点。

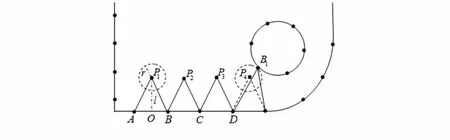
图4 新节点生成

2.3.3 更新前沿序列

记更新过程中的外边缘前沿为W′。当AB处生成前沿点P1后，将P1点加入到原来序列末尾， 从BC处继续更新前沿，生成P2点，放入W′序列末尾，同时舍弃B点，从CD处开始更新，逐渐完成更新过程。

2.4 内外边界合并

易知W′序列中的元素在更新过程中会不断减少，在NW1≤NW′≤2NW1时，根据公式

(7)

设置ε的值，找出合适的W′，此时表示2个点序列已较接近。

2.5 网格整体优化

通过以上步骤，生成的网格已具有较好的几何特性。在此基础上，采用Laplace光顺化方法，对全局网格做了进一步优化

(8)

其中,(xi,yi)为i点坐标，(xk,yk)为共享该点的所有三角形顶点坐标,ω为一个控制网格疏密的系数，n为共享该点的三角形顶点个数。

3 实验分析

如图5所示，本文搭建了由旋转对称激光三角传感器、电控平移台、步进电机控制器、光源控制器组成的实验平台。为了验证视觉引导方法的有效性，如图6所示，选用了3个常见工件，分别记为1，2，3，并进行了网格生成和三维重建实验。工件1最大外半径为20 mm，工件2长、宽分别为30，25 mm，工件3长、宽分别为40，38 mm。

图5 系统实验平台

图6 CCD获取的工件灰度图

对3组工件进行边缘提取，得到图7中所示结果。有些物体在边缘提取后会有一些细小断裂曲线，但在后续边界分块和离散化处理时，本文的工作主要基于闭合曲线，因此，这部分误差不会影响网格生成和三维重建的结果。

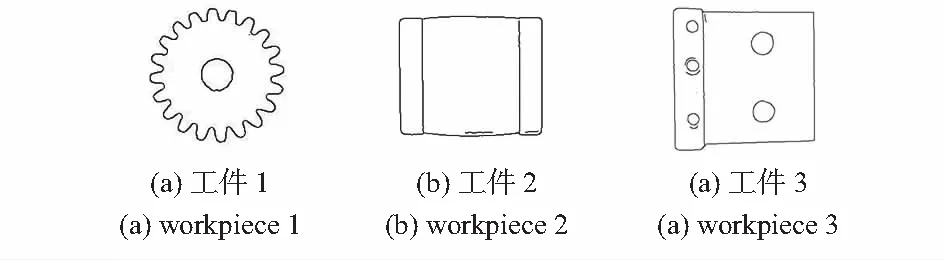
图7 工件边缘提取后图像

本文中使用的CCD分辨率为1280×1024，对CCD进行标定，计算出原始图像中长和宽的一个像素单位在当前实验平台下近似代表了0.06 mm。而在AFT离散边界时，首先需要将图像压缩设置尺寸单元，为了使像素单位对应的实际距离易于计算，分别尝试将原图像做4,5,8,10倍压缩，进行边界离散,则压缩后的一个像素单位分别表示实际中0.24,0.3,0.48,0.6 mm。本文中使用了大恒GCD—105200M电控平移台和GCD—0301M型步进电机控制器，其单脉冲分辨率为1 μm，可以完成对各个工件的视觉引导测量。以工件1为例，通过实验，在4倍和5倍压缩情况下，采样点数太多，在8倍和10倍的压缩情况下，得到网格如图8所示，分别包含2512和1192个测量点。从生成网格可看出:生成网格较好地表示了物体的几何特征，在边缘点处网格稠密，测量的点较多，物体中间平坦处测量点分布稀疏，整个区域节点分布合理。

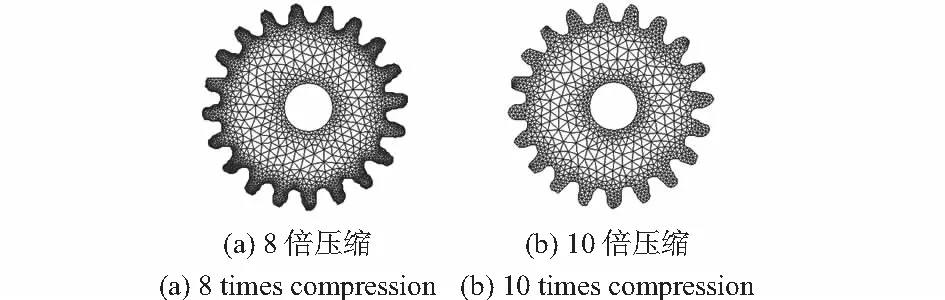
图8 不同压缩倍率下工件1网格生成图

根据所获得的测点坐标，进行了三维重建实验。旋转对称激光三角传感器和CCD传感器已集成为整体，配准关系已知，据此确定图像坐标原点，控制旋转对称激光三角传感器到指定坐标进行测量，同时将获取的深度数据保存至txt文档。完成测量后，利用OpenGL进行三维重建，如图9所示。

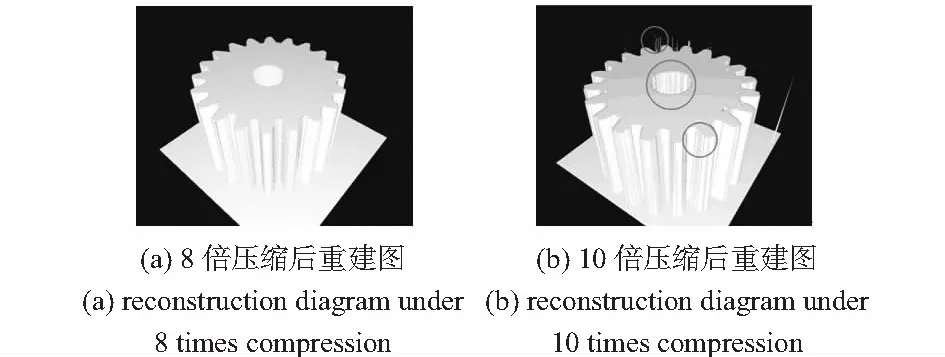
图9 工件1在不同压缩倍率下的三维重建效果图

通过图9结果可以看出:8倍压缩情况下的工件1重建效果好于10倍压缩情况。边缘和中心圆孔较光滑，没有条纹状，基本达到重建要求。同时给出了一种均匀步长测量下的重建结果。为了便于计算，将电控平移台的步长设置为0.5 mm，工件1最大外半径为20 mm，因此,均匀测量需要80×80共计6400点。从重建效果图10看，均匀测量下的重建结果和8倍压缩下的重建结果(图11)，无明显差距。因此,认为对于本方法，8倍压缩为一个合适的、可以通用的压缩比率。

图10 工件1逐点扫描测量下三维重建效果图

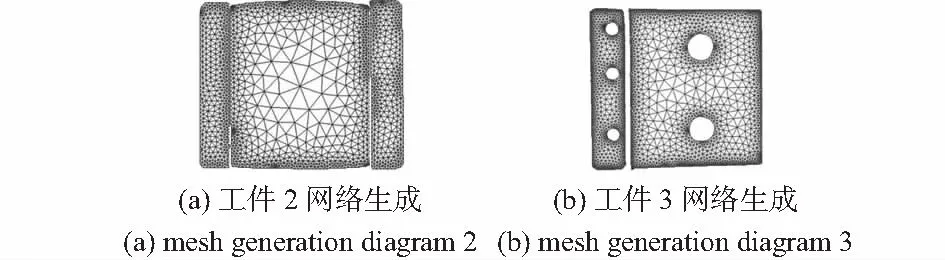
图11 工件2,3在8倍压缩下网格生成图

以8倍为压缩比，对工件2,3分别进行了网格生成(图11)。受AFT算法限制，工件2和工件3均被分块处理，但分块各部分边界坐标仍然从原图像中获取，生成的节点坐标依然为原图像中坐标。因此,在后期利用旋转对称激光三角传感器进行测量时，不同区域有着相同的配准关系。最后得到的三维重建结果如图12所示。

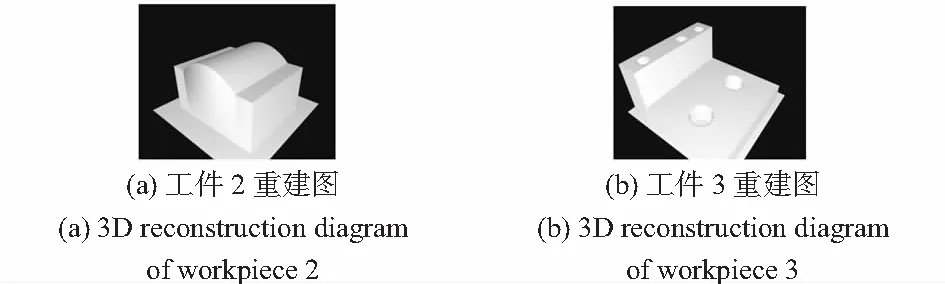
图12 工件2,3三维重建效果图

工件2和工件3的尺寸已知，结合电控平移台0.5 mm的步进值，表1给出了它们在视觉引导方法和均匀测量方法下的测量点数，并计算了测量效率的提高率。对于工件2，因工件尺寸相对较小，均匀扫描下测量点数少，测量效率提高有限，对于工件1,3，测量效率均提高50 %以上。

表1 视觉引导对测量效率的提升

4 结 论

本文设计了一种视觉引导的激光测量方法，旨在优化点激光的测量过程，减少测量点数。本文使用改进的AFT方法，在获取的物体边缘基础上向内部推进，得到分布合理的特征点，指导激光三角传感器进行测量。实验结果表明：对于常用工件，在与逐点均匀扫描相近的重建效果下，测量效率至少可提高40 %以上。

参考文献:

[1] 王晓嘉,高 隽,王 磊.激光三角法综述[J].仪器仪表学报,2004,25(4):601-604.

[2] Francisco Javier Brosed,Juan Jose Aguilar,David Guillomia,el al.3D geometrical inspection of complex geometry parts using a novel laser triangulation sensor and a robot[J].Sensors,2011,11:90-110.

[3] 张 洪,熊汉伟,张湘伟.视觉引导下的自由曲CMM测量[J].机床与液压，2008,36(8):206-208.

[4] Son Seokba E,Kwan Seungman Kim,Lee H.Path planning of multi-patched freeform surfaces for laser scanning[J].The International Journal of Advanced Manufacturing Technology，2003(22):424-435.

[5] Ott P,Gao J,Eckstein J,el al.A rotationally symmetric triangulation sensor with low cost reflective optics[C]∥IEEE International Conference on Information Acquisition,Macau,China,2005:72-76.

[6] Eckstein Johannes.Optical and mechanical design of a rotationally symmetric triangulation sensor with an integrated vision sys-tem[D].Hefei:Hefei University of Technology,2008.

[7] Wang Xiaojia,Gao Jun,Wang Lei,el al.Robust processing me-thod for rotationally symmetric triangulation sensor[J].Chinese Journal of Scientific Instrument,2007,28(2):203-211.

[8] Lo S H.Dynamic grid for mesh generation by the advancing front method[J].Computers and Structures,2013,123:15-27.