CAS-1模拟月壤动剪切模量与阻尼比的试验研究

张 宇，余 飞，陈善雄，李 剑

（中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071）

1 引 言

我国探月工程分为 “绕、落、回”3个阶段，“月壤采样”是探月3期工程的核心，目标是取得具有层理品质的月壤样品，但在取样过程中将面临的关键问题是月面特殊环境条件下钻取装置与月壤相互作用的动力响应问题。由于月壤样品极其珍贵，即便是拥有381 kg月壤样品的美国对其使用也是非常严格和谨慎的，因此，需优选一种与真实月壤力学性质相近的“模拟月壤”[1]，开展相关的基础性力学试验研究。

国内外诸多学者[1－12]针对不同的模拟月壤分别做了许多相关的物理、力学性质的研究。郑永春等[2]主要是对CAS-1模拟月壤的微波介电特性进行了研究；李建桥等[7－8]以吉林火山灰为原料研制成的模拟月壤，讨论了其基本物理力学性质；蒋明镜等[9－10]探讨了颗粒级配和含水率对 TJ-1模拟月壤力学性质的影响，并开展了关于TJ-1模拟月壤承载特性的试验研究；Haydar等[11]对模拟月壤 JSC-1的拉伸特性进行了试验，探讨模拟月壤重度和厚度对抗拉强度的影响；Robert等[12]对模拟月壤的微观结构进行了观察分析，并致力于对模拟月壤力学性质的改进研究。

以上研究均偏向模拟月壤静力学方面的研究，主要关心其基本的物理力学性质，而与月壤钻取采样相关的动力学性质方面的研究涉及较少，因此，本文将采用中国科学院地球化学研究所与国家天文台合作研制成功的 CAS-1模拟月壤（国家标准样品），代替真实月壤开展相关的基础性动力学试验研究。由于土的动剪切模量和阻尼比是土动力特性首要的两个参数，是土层动力特性分析中必备的动力参数。因此，开展模拟月壤动剪切模量和阻尼比的动力特性分析，是研究月壤与采样装置相互作用的重要基础。

2 试验方案

2.1 试验设备

试验仪器为英国GDS公司生产的固定-自由型Stokoe 共振柱（RCA），是目前国际上最常用的共振柱试验仪之一，其原理详见柏立懂[13－14]的研究。

2.2 试验材料

试验材料采用中国科学院地球化学研究所与国家天文台合作研制成功的CAS-1模拟月壤（国家标准样品）[2]。CAS-1模拟月壤的颗粒形态表现为典型的研磨形成的颗粒特征，为尖锐棱角状（图1(a)）[2]，与国际著名的 JSC-1模拟月壤的颗粒形态相似（图 1(b)）[3]，均具有明显的研磨痕迹，但不同于月壤颗粒的形态（1(c)）[3]，这是由于真实月壤在月表空间的广度和深度的分布不同，且经历的风化程度和成熟度不同，月壤的颗粒形态极为多变，从圆球状、椭球状到极端棱角状都有出现，而 CAS-1模拟月壤的颗粒形态表现为典型的研磨形成的颗粒特征，为尖锐棱角状。

试验前将模拟月壤颗粒全部烘干，通过比重瓶试验得到相对密度Gs=2.66，属于真实月壤颗粒相对密度（2.3～3.2）[15]范围；将0.075 mm以下的模拟月壤颗粒用密度计法分析其颗粒组成，0.075 mm以上的颗粒用筛分析法测试颗粒组成，结果与真实月壤[6,9]以及国内外著名模拟月壤[4－9]相比较，详见图2和表1。

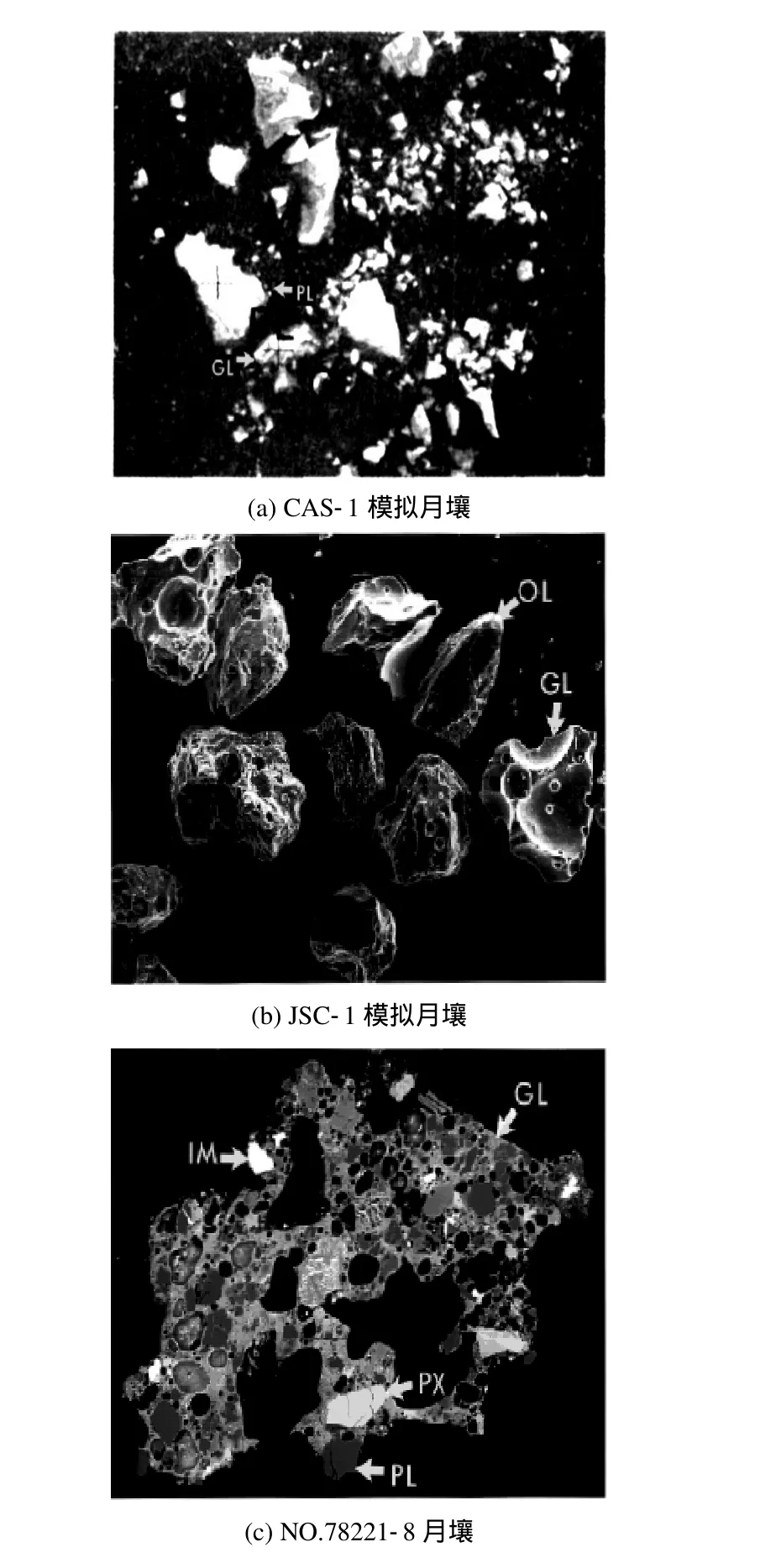
图1 CAS-1、JSC-1模拟月壤与月壤颗粒形态（扫描电镜图）Fig.1 Particle morphologies of CAS-1, JSC-1 simulated lunar soil and real lunar soil (scanning electron micrographs)

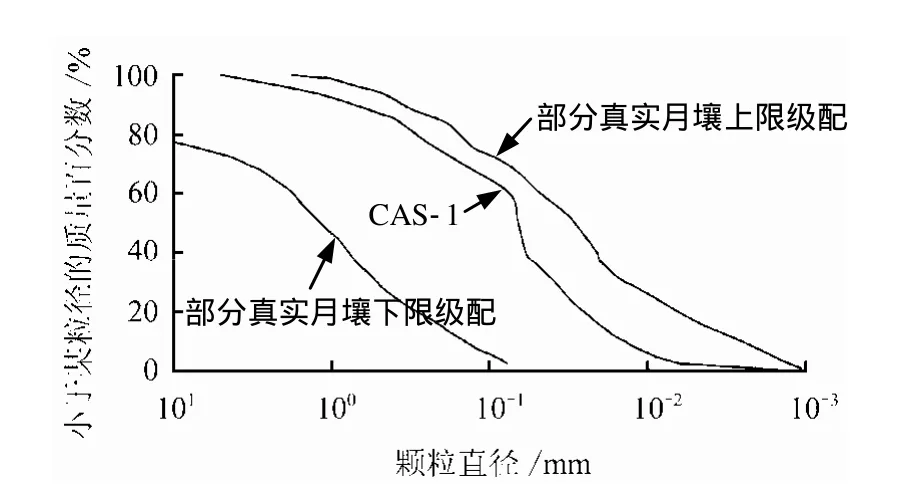
图2 CAS-1模拟月壤与部分真实月壤[6, 9]的粒径级配曲线Fig.2 Gradation curves for CAS-1 lunar soil simulant and parts of real lunar soil

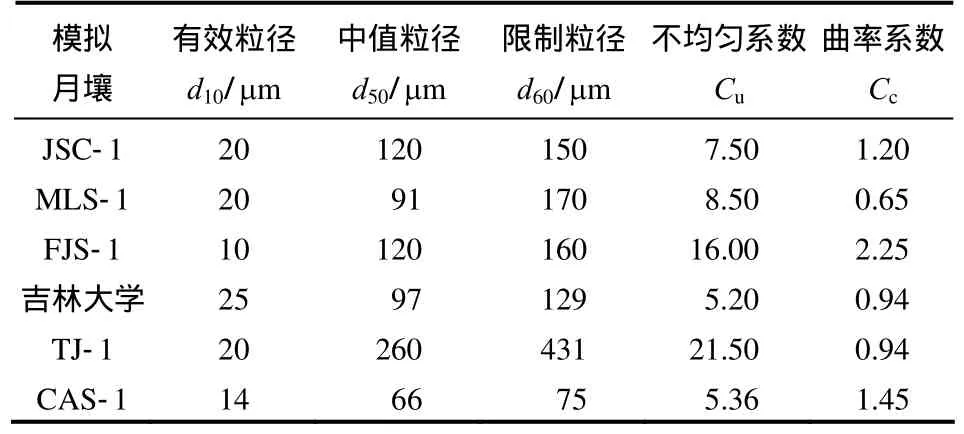
表1 模拟月壤[4－9]颗粒组成比较Table 1 Comparison of composition for simulated lunar soil particles

图2说明，CAS-1模拟月壤颗粒粒径级配基本分布于部分真实月壤（源自Apollo和Luna计划）的上下限级配之间，颗粒组成属真实月壤范畴；表1说明，CAS-1模拟月壤的颗粒组成与国内外著名的模拟月壤的颗粒组成相差不大，各项参数分布居中，并且与吉林大学模拟月壤相近（原材料均源自吉林火山群）。

2.3 试样制备

试验前将模拟月壤试样烘干，且在室温条件下干燥冷却。按照控制模拟月壤孔隙比的方法，设置两种不同松散状态的孔隙比e分别为1.0和0.8，根据相对密度计算出相应的初始干密度ρd分别为1.33 g/cm3和 1.48 g/cm3。

由于 CAS-1模拟月壤是一种类似地面粉细砂的多孔材料物质，且要求在完全干燥的状态下开展试验研究，若采用传统的制样方法易出现试样不易成型、不均匀、稳定性差以及不能很好地实现仪器的安装等情况，且对试验结果影响较大。因此，本次试验采用以下特定试样制备方法，以减小以上情况对试验的影响。

将试样在共振柱仪的底座上原位成型：在底座上套上橡皮膜，利用橡皮筋固定，安装好试样对开模具（以下简称“对开模”），将橡皮膜顶部翻卷到对开模外壁上，打开微型真空泵，提供20 kPa的负压，使橡皮膜紧贴在对开模内壁上；采用插捣砂雨法，利用漏斗将称好的试样分5层均匀地洒入橡皮膜内部，并利用细铁丝进行插捣，考虑到击实上层砂土对下层有增密作用，土层控制击实厚度向上逐层适当递减，使每层的试样都能均匀密实；在橡皮膜内装样到指定高度（100 mm）后，削平试样顶面或完成最后一层砂土的击实后，将土样帽轻轻平放到土样顶面，扣上土样薄膜并套上橡皮筋，在仪器底座的孔压通道通过微型真空泵施加20 kPa的负压以支撑试样，拆除对开模，试样成型，见图 3(a)；分别测量试样5个不同高度位置的2处直径，取其平均值；并分别测量试样的3个不同位置的高度，取其平均值，试样为直径(50.00±0.10)mm、高度(100.00±0.20)mm的实心圆柱体；待试样安装完毕后，先将负压减小10 kPa，再施加10 kPa围压，循环两次以消除负压，见图3(b)。

图3 试验准备Fig.3 Test preparation

2.4 试验方法

试验时使用的围压分别设置为低围压（25、50、75、100 kPa）和常规围压（150、200、250、300 kPa）两种应力状态。由于设置的孔隙比是1.0和0.8，试样孔隙比均较大，为了保证试验过程中剪应变控制在 10-6～10-4之间变化，经过反复调试后将试验开始时的激励电压设置为0.001、0.002、0.003、0.005、0.007、0.010、0.015、0.020、0.030 V，该激励电压适用于CAS-1模拟月壤。每级围压测试前，先稳定30 min，待置于转动盘上的LVDT传感器监测试样的轴向沉降量保持稳定后进行试验。

3 试验结果

在不同的稳定围压下，不同密实程度的模拟月壤的动剪切模量G与剪应变γ的关系曲线如图4所示。由图可见，G随着γ的增大而逐渐减小，当剪应变较小时，G减小得较缓慢，而当剪应变增大到一定程度，动剪切模量开始快速减小。动剪切模量随剪应变的这种变化趋势，反映了土的动应力-应变关系的非线性、滞后性的规律[16]。

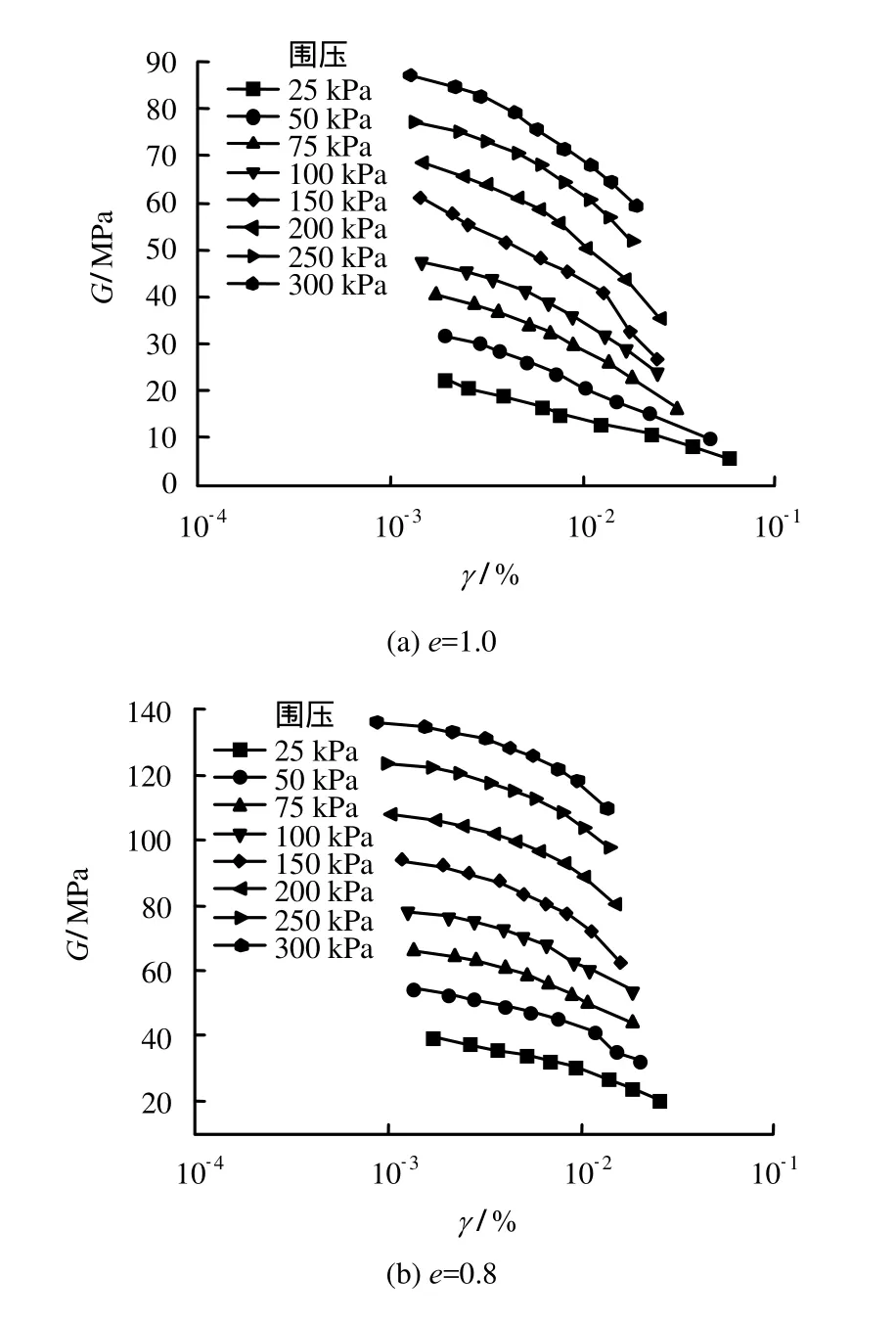
图4 模拟月壤动模量G和剪应变γ 的关系Fig.4 Relationships between dynamic modulus G and shear strain γ of lunar soil simulant

对比不同围压的试验结果可以看到，G随围压减小而减小。在同一激励电压下，其剪应变更大，动剪切模量随剪应变增大而减小的趋势更为显著。

对比不同孔隙比的试验曲线可以看到，孔隙比越大，G越小，在同一激励电压下，其剪应变更大，动剪切模量-剪应变曲线更为陡峭，即随剪应变增大而快速减小，无明显的平缓阶段。

图5为不同密实程度的模拟月壤在不同围压下的阻尼比λ随剪应变γ的变化曲线。从图可以看出，阻尼比均随剪应变的增大而增大，且当剪应变增大到一定程度，阻尼比会急剧增大，对比图4可以看到，动剪切模量快速减小的阶段，也是阻尼比快速增大的阶段。

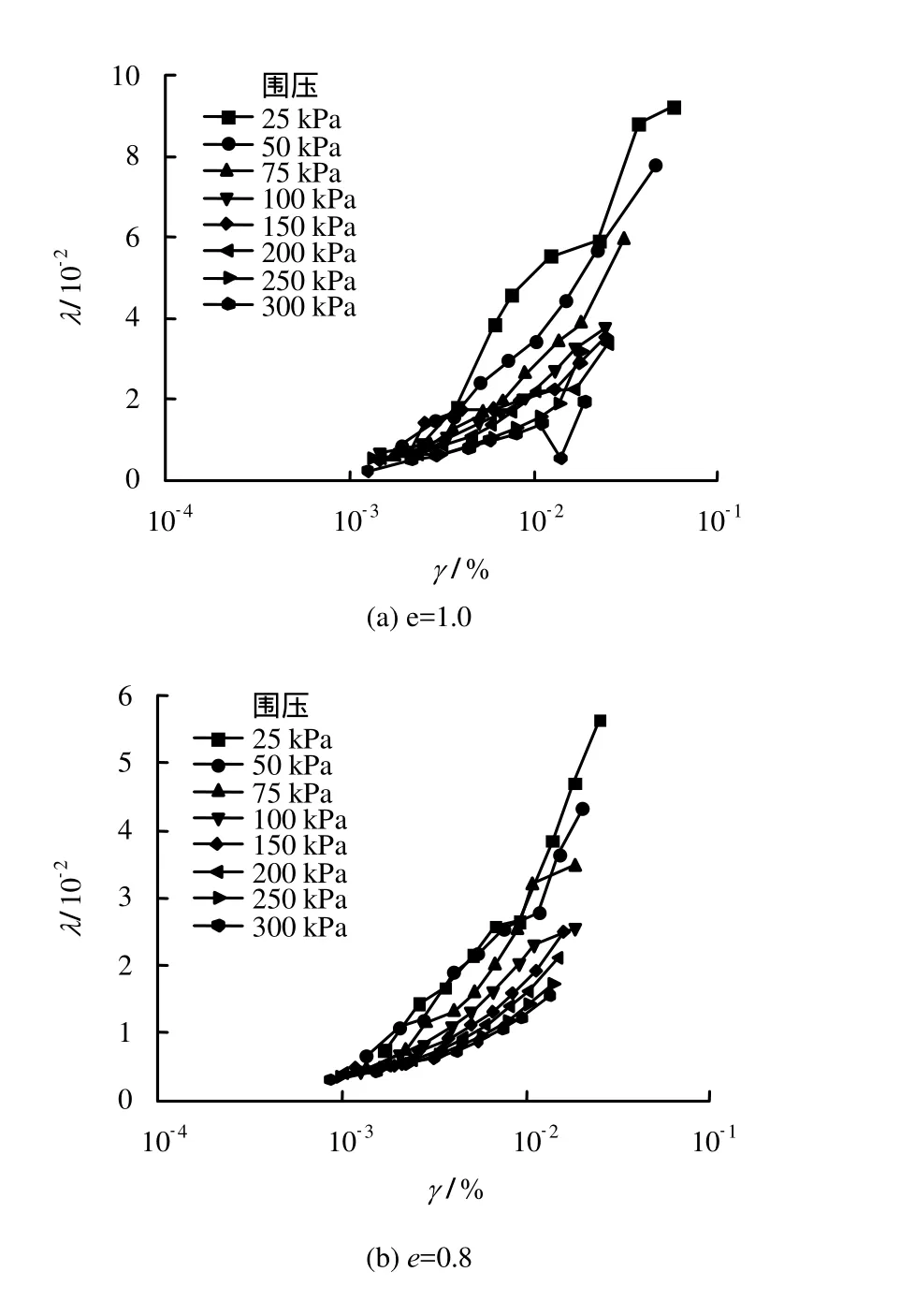
图5 模拟月壤阻尼比λ 与剪应变γ 的关系Fig.5 Relationships between damping ratio λ and shear strain γ of lunar soil simulant

对比不同围压的试验结果可以看到，在围压越小，阻尼比越大，这种变化在小剪应变条件下，围压的影响较小，随着剪应变的增大，围压对阻尼比的影响急剧放大。

对比不同孔隙比的试验结果可以看到，孔隙比越大，阻尼比越大，阻尼比随剪应变的变化曲线更为陡峭。

上述试验结果表明，应力水平和密实程度对模拟月壤的动剪切模量G、阻尼比λ存在显著的影响，在真实月面环境，应力水平很低、孔隙比较大的条件下，月壤颗粒之间的接触点较少，使得应力波在月壤中的传播较慢，表现为较小的G和较大的λ，且随着剪应变的增大，动剪切模量快速减小，阻尼比急剧增大，这一特性对月壤钻取采心率和样品的完整性带来显著的影响。

4 试验结果分析

4.1 试验数据分析

试验结果表明，试验曲线的规律性很好，其动应力-应变关系可采用著名的 Hardin-Drnevich[17]双曲线模型来描述：

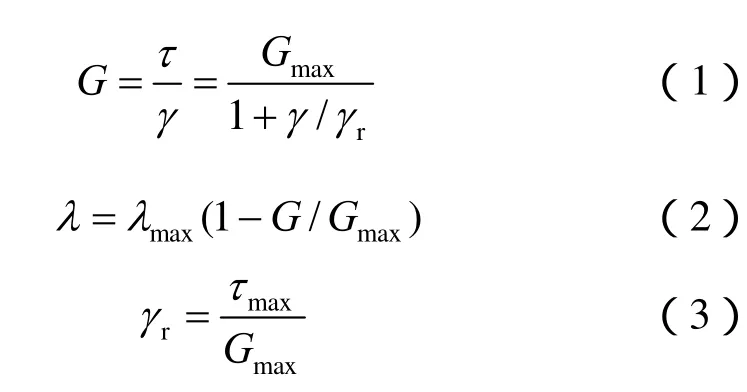
所以，有

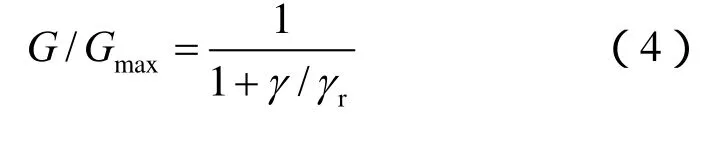
式中：τ、γr分别为动剪应力、参考剪应变；Gmax、λmax、τmax分别为最大动剪模量、最大阻尼比、最大动剪应力，Gmax和λmax可由共振柱试验测得，如表2所示。

由试验测得的动剪切模量、阻尼比与剪应变的试验数据关系，利用式（1）～（5）和最小二乘法进行回归分析，对不同试验回归得到的结果进行平均化处理[18－19]，结果如图6和表2所示。

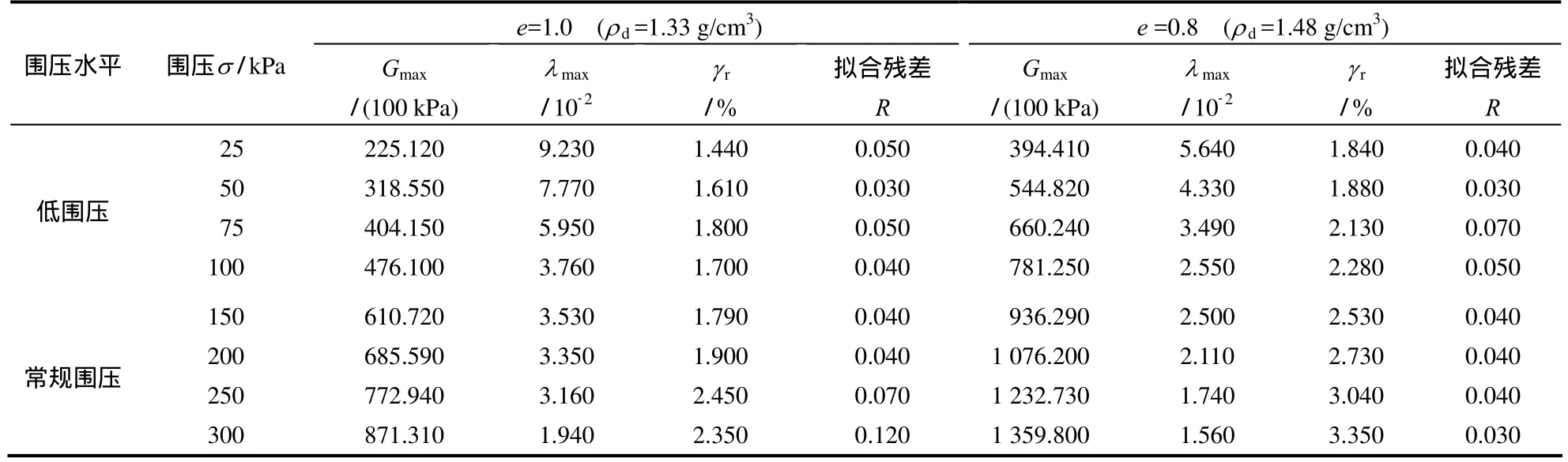
表2 不同孔隙比的CAS-1模拟月壤在不同围压下的平均化处理后的试验结果Table 2 Equalization after the treatment of experimental results with different void ratios of lunar soil simulant under different confining pressures

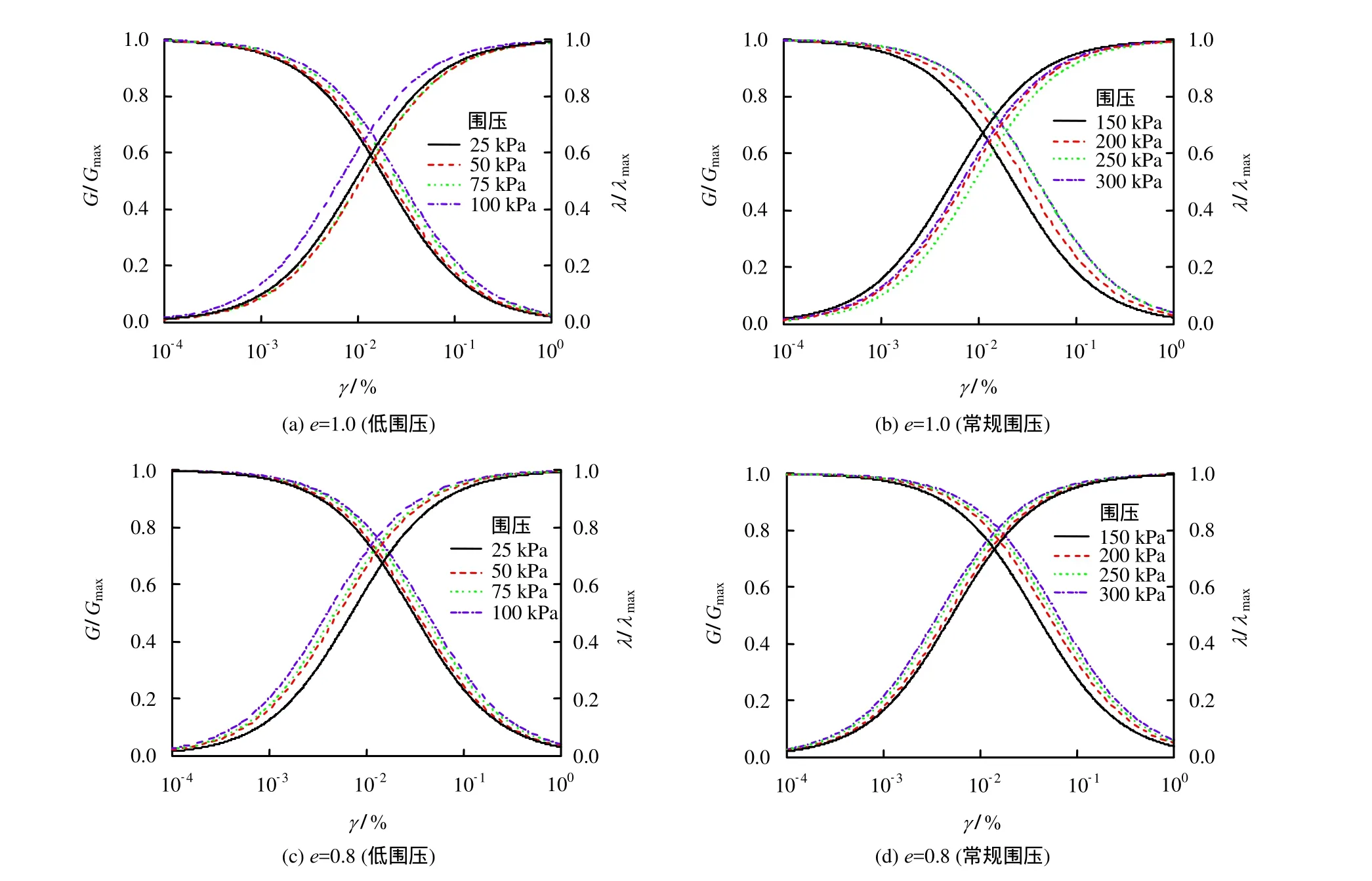
图6 不同孔隙比的CAS-1模拟月壤在不同围压下的G/Gmax-γ 和λ /λ max-γ 试验曲线Fig.6 G/Gmax-γ and λ /λ max-γ experimental curves of different pore ratios of lunar soil simulant under different confining pressures

以上图表中设置低、常规围压，反映的是月壤钻取采样过程中月壤层不同深度范围内的应力水平，所以认为低、常规围压分别代表月表浅、深层月壤。而在钻取采样深度范围内（一般为3～5 m），其应力水平在0～25 kPa区间。

图6是CAS-1模拟月壤动剪切模量G经过归一化后的G/Gmax-γ以及λ/λmax-γ最小二乘拟合关系曲线。G经过归一化后，在不同围压下的所有试验点都集中于一个很小的条带内，试验点离散性较小。因此，可以认为，模拟月壤的动剪切模量对其最大动剪切模量具有较好的归一性。由表2还可知，图6中动力学参数经过最小二乘回归分析后，整体拟合效果较好，说明 Hardin-Drnevich 双曲线模型适合于模拟月壤动力本构的描述。

动剪模量G经过归一化处理后的动剪切模量比G/Gmax，随剪切应变γ的增大而减小，随围压的升高（月壤层深度的增加）而增大，这与动剪切模量与剪应变的关系特点保持一致，且CAS-1模拟月壤在相同密实状态下反映浅层月壤（低围压）的动剪切模量比的拟合曲线较深层月壤（常规围压）更集中，归一性更好；同样深度范围内的CAS-1模拟月壤，密实程度对动剪切模量比曲线的离散性影响不大。

在同样深度范围内，随模拟月壤孔隙比的变小，试样愈密实，λ/λmax-γ的关系曲线分布愈宽，回归结果相对于动模量比更离散；但相同孔隙比的模拟月壤在不同深度范围内的回归结果相差不大，说明模拟月壤孔隙比对λ/λmax-γ的关系影响较大。

4.2 Gmax的变化规律

由图7可知，孔隙比分别为1.0和0.8两种密实状态的 CAS-1模拟月壤的 Gmax与围压σ（25～300 kPa）具有良好的线性关系，均随σ的增加而增大，其表达式为

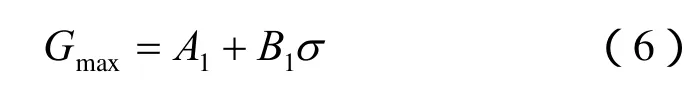
式中：A1为直线的截距；B1为直线的斜率。A1、B1的值列于表3。

CAS-1模拟月壤的 Gmax随围压σ的递增保持良好的线性增长的原因，是由于围压逐渐增大，模拟月壤颗粒之间的接触面积增大，应力波则传递得更快，Gmax逐渐增大，从而在相同围压下孔隙比越小的试样，颗粒之间接触愈紧密，Gmax愈大，且根据图 7的线性拟合结果，可以认为在更低围压范围内（0～25 kPa），CAS-1模拟月壤Gmax与围压σ仍然保持良好的线性关系。因此，可结合式（6）和表3的参数值，反推出1.0和0.8两种孔隙比状态的试样在 0～25 kPa围压范围内的 Gmax值，分别是：21.908～27.583 MPa和 38.518～47.006 MPa。

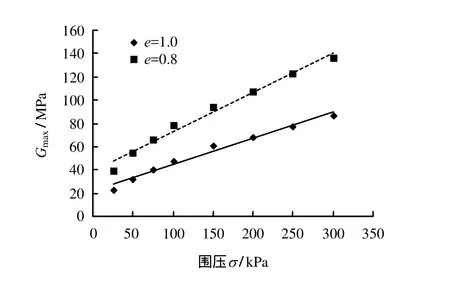
图7 Gmax与围压σ 关系Fig.7 Relationships between Gmax and confining pressure σ

表3 Gmax与围压σ 的拟合结果Table 3 Fitting results of Gmax and confining pressure σ

4.3 λmax的变化规律

图8反映的是孔隙比分别为1.0和0.8两种密实状态的CAS-1模拟月壤的λmax与围压σ的关系。在低围压范围内（25～100 kPa），λmax均随σ的增加而快速递减，而且从图中可以看出，两者成一定的线性关系，且e=1.0的试样线性递减得更快；进入常规围压范围（100～300 kPa）后，CAS-1模拟月壤的最大等效滞回黏弹性阻尼比λmax随σ的关系较之前发生了明显的转折，λmax随σ增加呈缓慢下降的规律。对这两个阶段的λmax随σ变化的规律分别用线性关系描述，统一的表达式为

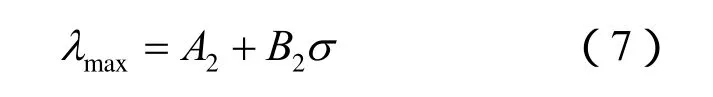
低、常规围压的A2、B2的值列于表4。

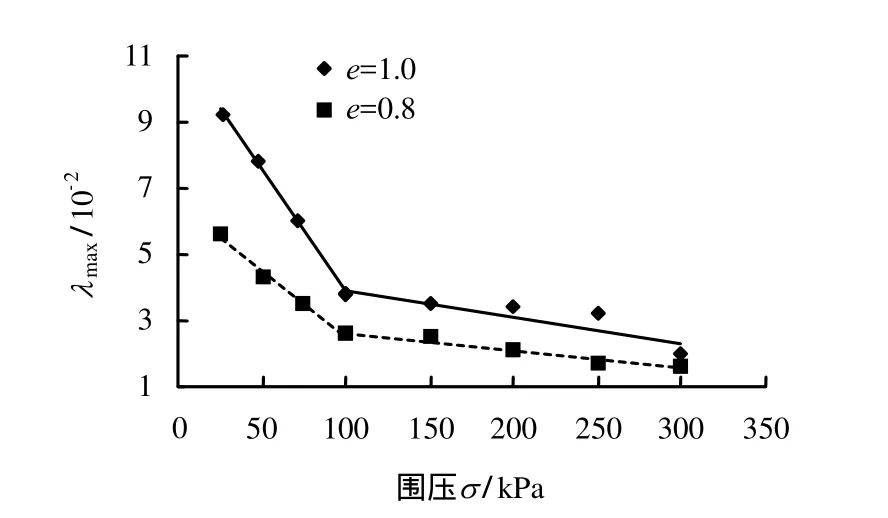
图8 λmax与围压σ 关系Fig.8 Relationships between λmax and confining pressure σ

表4 λmax与围压σ 的拟合结果Table 4 Fitting results of λmax and confining pressure σ

由图8可以看出，σ的大小对CAS-1模拟月壤的λmax变化规律有明显的影响。λmax随σ的递增发生图8中两个阶段变化规律的原因：共振柱试验仪是采用试样底端固定、顶端带电极自由振动的工作原理；在地面低围压下，试验开始时试样顶端将会出现振动变形较大，且具有向塑性发展的趋势，不能将材料内部的振动波顺利地传导到试样底部进行能量耗散，于是在低围压下CAS-1模拟月壤表现出较大的阻尼比，以便耗散更多的振动变形能量，因此，低围压下表现出更高的阻尼比；随着围压的升高，直至进入常规围压状态，试样颗粒之间连接越来越密实，且整体性越来越好，此时来自试样顶端的振动波将会均匀地传导到试样底部，并且随着围压的升高，试样振动变形亦受到抑制，从而CAS-1模拟月壤表现出较低且平缓的阻尼比发展规律。试样为e=1.0较e=0.8的阻尼比高，反映了材料孔隙比愈大，相同围压下振动变形愈大，试样将表现出更大阻尼比耗散振动变形的能量，并结合式（7）和表4的参数值，反推出1.0和0.8两种孔隙比状态的试样在 0～25 kPa围压范围内的λmax值，分别是11.240×10-2～ 9.415×10-2和 6.530×10-2～ 5.520×10-2。

4.4 参考剪应变γr 的变化规律

图9反映的是孔隙比分别为1.0和0.8两种密实状态的CAS-1模拟月壤的参考剪应变γr（拟合参数）与围压σ具有良好的线性关系，且压σ的增大而增大。统一的表达式为

A3、B3的值列于表5。

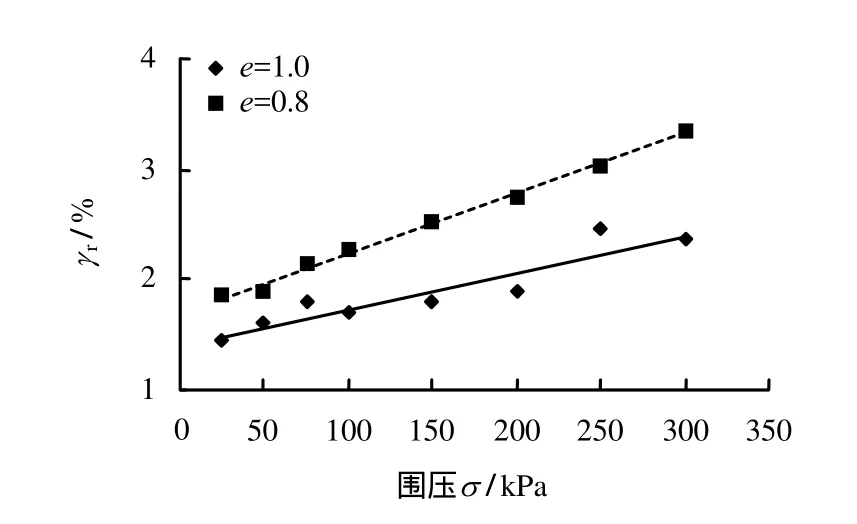
图9 γ r与围压σ 关系Fig.9 Relationships between γ r and confining pressure σ

表5 γ r与围压σ的拟合结果Table 5 Fitting results of γ r and confining pressure σ

根据图9的线性拟合结果可以认为，在更低围压范围内（0～25 kPa），CAS-1模拟月壤γr与σ仍然保持良好的线性关系。因此，可结合式（8）和表5的参数值，反推出1.0和0.8两种孔隙比状态的试样在0～25 kPa围压范围内的γr值，分别为1.407%～1.489%和1.685%～1.822%。

4.5 模拟月壤G/Gmax和λ 的推荐值

由于钻取采样过程中随月壤层深度的递增，周围的应力水平将越高，因此，围压的范围值可以在一定程度上反映月壤的采集深度。结合试验结果以及拟合曲线，将以上两种孔隙比的试样随围压变化得到的应变范围内的相关试验结果分别列于表 6和表7作为推荐值，这对于月壤采样具有一定的参考意义。

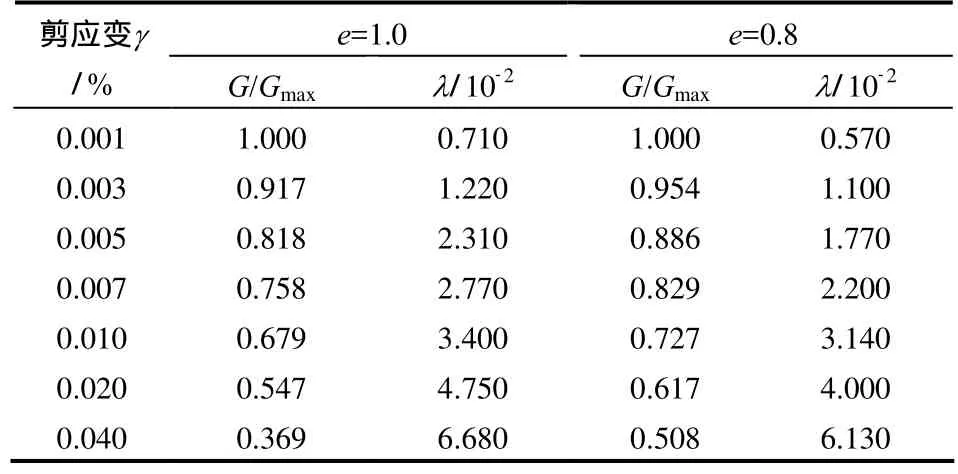
表6 模拟月壤 G/Gmax , λ 与γ 的推荐值（0～100 kPa）Table 6 Recommended values of G/Gmax, λ and γ of the lunar soil simulant ( 0-100 kPa )

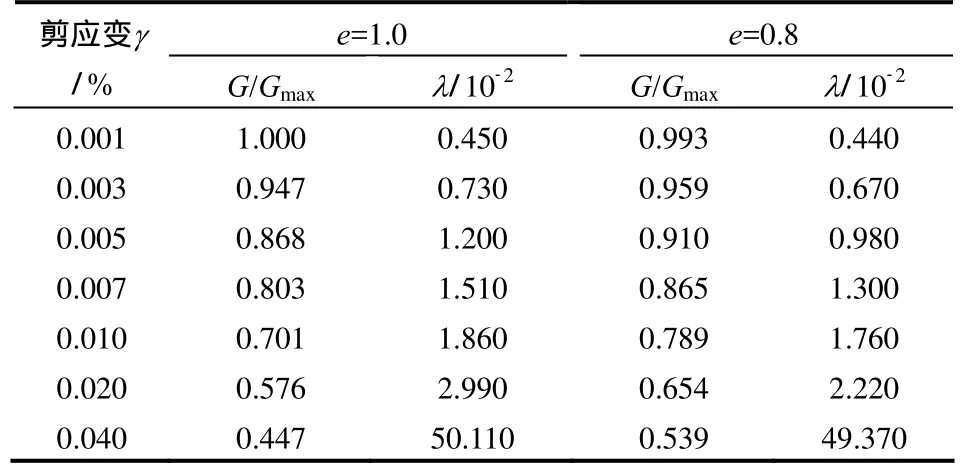
表7 模拟月壤 G/Gmax与γ 和λ 与γ 的推荐值（100～300 kPa）Table 7 Recommended values of G/Gmax, λ and γ of the lunar soil simulant ( 100-300 kPa)

5 结 论

（1）通过与真实月壤以及国内外著名模拟月壤对比研究，CAS-1模拟月壤在颗粒形态与颗粒组成属部分真实月壤范畴，适用于动力学试验研究；开展GDS共振柱试验，弄清了不同孔隙比、不同围压对动剪切模量G及阻尼比γ的影响规律。

（2）应力水平和密实程度对模拟的动G、λ存在显著的影响，在真实月面环境、应力水平很低、孔隙比较大的条件下，表现为较小G和较大的λ，且随着剪应变的增大，动剪切模量快速减小，阻尼比急剧增大，这一特性对月壤钻取采心率和样品的完整性带来显著的影响。

（3）采用Hardin-Drnevich双曲线模型对试验数据进行分析，得到了孔隙比分别为 1.0和 0.8的CAS-1模拟月壤，分别在低、常规围压下的G/Gmax与 λ/ λmax随γ变化的平均拟合曲线，以及相关的动力学参数值。

（4）定量分析了孔隙比为1.0和0.8两种状态下Gmax、λmax和γr与围压σ相关关系式，并据此给出了月壤钻取采样深度范围内（一般为3～5 m，应力水平在0～25 kPa区间）月壤的Gmax、λmax和γr的值，即 Gmax为 21.908～27.583 MPa和 38.518～47.006 MPa，λmax为 11.240×10-2～9.415×10-2和6.530×10-2～5.520×10-2，γr为1.407%～1.489%和1.685%～1.822%。

上述研究给出的 CAS-1模拟月壤相关的动力学参数推荐值，对月壤采样过程的地面模型试验以及数值模拟研究起到较好的借鉴和参考作用。

[1]KIRKICI H, ROSE M F, CHALOUPKA T. Experimental study of simulated lunar soil: High voltage breakdown and electrical insulation characteristics[J]. IEEE Transactions on Dielectrics and Electrical Insulation,1996, 3(1): 119－125.

[2]郑永春, 王世杰, 冯俊明, 等. CAS-1模拟月壤[J]. 矿物学报, 2007, 27(3/4): 571－578.ZHENG Yong-chun, WANG Shi-jie, FENG Jun-ming,et al. CAS-1 lunar soil stimulant[J]. Acta Mineralogica Sinica, 2007, 27(3/4): 571－578.

[3]DAVID S MCKAY, JAMES L CARTER, WALTER W WOLES. JSC-1: A new lunar soil stimulant[C]//Engineering, Construction, and Operations in Space IV.New York: [s. n.], 1994: 857－866.

[4]WILLMAM B M, BOLES W W, MCKAY S, et al.Properties of lunar soil stimulant JSC-1[J]. Journal of Aerospace Engineering, 1994, 8(2): 77－87.

[5]KLOSKY J L, STURE S, KO H Y, et al. Mechanical properties of JSC-1 lunar regolith simulant[C]//Proceedings of the Fifth International Conference on Space 96 Albuquerque. New York: [s. n.], 1996: 680－688.

[6]PERKINS S W, MADSON C R. Mechanical and load-settlement characteristics of two lunar soil simulants[J]. Journal of Aerospace Engineering, 1996,9(1): 1－9.

[7]李建桥, 邹猛, 贾阳, 等. 用于月面车辆力学试验的模拟月壤研究[J]. 岩土力学, 2008, 29(6): 1557－1561.LI Jian-qiao, ZOU Meng, JIA Yang, et al. Lunar soil simulant for vehicle-terramechanics research in laboratory[J]. Rock and Soil Mechanics, 2008, 29(6):1557－1561.

[8]邹猛, 李建桥, 刘国敏, 等. 模拟月壤地面力学性质试验研究[J]. 岩土力学, 2011, 32(4): 1057－1061.ZOU Meng, LI Jian-qiao, LIU Guo-min, et al.Experimental study of terra-mechanics characters of simulant lunar soil[J]. Rock and Soil Mechanics, 2011,32(4): 1057－1061.

[9]蒋明镜, 李立青, 刘芳, 等. 含水率和颗粒级配对TJ-1模拟月壤力学性能影响的试验研究[J]. 岩土力学, 2011,32(7): 1921－1925.JIANG Ming-jing, LI Li-qing, LIU Fang, et al. Effects of moisture content and gradation on mechanical properties of TJ-1 lunar soil stimulant[J]. Rock and Soil Mechanics,2011, 32(7): 1924－1925.

[10]蒋明镜，戴永生，张熇，等. TJ-1模拟月壤承载特性的现场试验研究[J]. 岩土力学，2013, 34(6):1529-1535.JIANG Ming-jing, DAI Yong-sheng, ZHANG He, et al.Field experimental research on bearing properties of TJ-1 lunar soil simulant[J]. Rock and Soil Mechanics, 2013,34(6): 1529－1535.

[11]HAYDAR ARSLAN, STEIN STURE, SUSAN BATISTE.Experimental simulation of tensile behavior of lunar soil stimulant JSC-1[J]. Materials Science and Engineering,2008, 478(1): 201－207.

[12]ROBERT J GUSTAFSON, MARTY A GUSTAFSON,RAYMOND A FRENCH, et al. Simulants for testing and verifying exploration surface activity[C]//American Institute of Aeronautics and Astronautics. San Jose: [s. n.],2006.

[13]柏立懂. 荷载历史对砂土最大剪切模量影响的共振柱试验研究[J]. 岩石力学与工程学报, 2011, 30(11): 2366－2374.BAI Li-dong. Effects of loading history on maximum shear modulus of sand by resonant column tests[J].Chinese Journal of Rock Mechanics and Engineering,2011, 30(11): 2366－2374.

[14]BAI L D. Preloading effects on dynamic sand behavior by resonant column tests[D]. Berlin: School of Planning Building Environment, Technical University of Berlin,2011.

[15]郑永春, 欧阳自远, 王世杰, 等. 月壤的物理和机械性质[J]. 矿物岩石, 2004, 24(4): 14－19.ZHENG Yong-chun, OUYANG Zi-yuan, WANG Shi-jie,et al. Physical and mechanical properties of lunar regolith[J]. Journal of Mineralogy and Petrology, 2004,24(4): 14－19.

[16]吴世明. 土动力学[M]. 北京: 中国建筑工业出版社,2000.

[17]HARDIN B O, DRNEVICH V P. Shear modulus and damping in soils: Measurement and parameter effects[J].Journal of the Soil Mechanics and Foundations Division, ASCE, 1972, 98(6): 603－624.

[18]袁晓铭, 孙锐, 孙静, 等. 常规土类动剪切模量比和阻尼比试验研究[J]. 地震工程与工程振动, 2000, 20(4):133－139.YUAN Xiao-ming, SUN Rui, SUN Jing, et al. Laboratory experimental study on dynamic shear modulus ratio and damping ratio of soils[J]. Earthquake Engineering and Engineering Vibration, 2000, 20(4): 133－139.

[19]蔡辉腾, 李英明, 欧秉松. 福州地区典型土动剪切模量与阻尼比的试验研究[J]. 岩土力学, 2010, 31(2): 361－365.CAI Hui-teng, LI Ying-min, OU Bing-song. Testing study of dynamic shear modulus and damping ratio of typical soils in Fuzhou area[J]. Rock and Soil Mechanics, 2010,31(2): 361－365.